Specific Enthalpy Based Heat Stress Index for Indoor Environments without Radiation Effect

LIU Shuxiao(刘书晓), LIU Yun(刘 赟), ZOU Yue(邹 钺)*

1 College of Environmental Science and Engineering, Donghua University, Shanghai 201620, China2 Dianwei Science Co., Ltd., Shanghai 201620, China

Abstract: Over 100 human thermal indices have been developed to predict the combined thermal impact on the body. In principle, these indices based on energy thermal budget equations should not only be the most complex but also be the most accurate. However, the simple indices based on algebraic or statistical models [e.g., the wet-bulb globe temperature (WBGT)] continue to be the most popular. A new heat stress index, the enthalpy dry-bulb temperature (EnD) for indoor environments is developed and validated in this study. The EnD index is unique in that it uses the air specific enthalpy, not the wet-bulb temperature, to measure the latent heat transfer from the skin to the surrounding environment. Theoretically, the EnD index can be treated as the equivalent temperature based on the convective heat transfer coefficient hc. Comparison is made between the EnD index and the widely used WBGT index based on the experimental data taken from three independent studies available in the scientific literature. The results show that the EnD index can reduce the overestimation of the dry-bulb air temperature and thus reduce heat stress in most cases, especially for hot and humid environments. It can be concluded that the EnD index has the potential to replace the WBGT index as the standard heat stress index in the future.

Key words: heat stress; wet-bulb globe temperature(WBGT); specific enthalpy; indoor environment; maximum allowable duration of heat exposure

Introduction

According to the World Health Organization (WHO), occupational heat stress is becoming a significant problem in several regions, and global climate change will make the situation worse. In addition to the significant public health threat, excessive heat exposure affects economic productivity and reduces the hourly work capacity[1-2].

The human heat strain response is the result of the interplay among many factors, which include the thermal state of the surrounding environment (e.g., air temperature, air velocity, humidity, and solar radiation), human physical and behavioral conditions (e.g., activity level, clothing, and posture), and individual characteristics. A large number of human thermal climate indices have been developed to predict the combined thermal impact on the body or the corresponding effects on physiological variables that differ according to the number of variables, sophistication level of the employed human body heat balance theory, and applications[3-5]. De Freitas and Grigorieva[4]sorted a total of 162 indices from the year of 1905 to the year of 2012 into eight primary classification classes: simulation devices for integrated measurement such as thermal manikins[6](group A: 11 indices); single-sensor indices such as the first thermal index (i.e., the wet-bulb temperature, which can be traced to Haldane[7]) (groups B: 6 indices); indices based on algebraic or statistical models such as the wet-bulb globe temperature (WBGT)[8](group C: 40 indices); two proxy thermal indices (strain and stress) such as the predicted four-hour sweat rate (P4SR)[9]and effective temperature (ET)[10](groups D and E: 28 indices); two energy thermal budget equation indices (strain and stress) such as the body-atmosphere energy exchange index (BIODEX)[11], and predicted heat strain (PHS)[12](groups F and G: 67 indices); special-purpose indices such as the draught risk index (DRI)[13](group H: 10 indices).

Groups F and G are the largest groups of indices, and they are based on human body heat balance equations. Normally, these kinds of indices apply all climatic and personal condition parameters as the input data for simulating the heat exchange between the human body and the ambient environment, and output the detailed information on the corresponding physiological reaction parameters. In principle, these indices are not the most complex accurate[14]. Current computational power allows meteorological data for even complex models to be handled on a handheld device. However, the simple indices in group C based on algebraic or statistical models (e.g., WBGT) continue to be the most popular indices[5, 15].

Most of the algebraic or statistical thermal climate indices in group C[4]include two or three of the following variables related to the different heat exchange processes between the human body and the ambient environment: dry-bulb temperaturetaand air velocity for convective heat transferVa; wet-bulb temperaturetwb, relative humidity (RH)RH, dewpoint temperaturetdew, and water vapor pressurePafor latent heat transfer; globe temperaturetgand solar radiationSfor radiation heat transfer; metabolic rateMand clothing insulationClofor describing the human body condition. Table 1 summarizes all parameters involved in 38 of 40 total indices; two Russian indices (i.e., the severity rating, and the thermal insulation characteristics of clothing) are not included because of the missing relevant literatures. In addition to above six fundamental parameters, the environmental air enthalpyHahas also been applied once as an index[16].

Table 1 Occurrence frequency of variables in 38 statistical indices of group C

Table 1 indicates that the different temperatures (ta,twb,tdew, andtg) are the most common variables applied in statistical indices. Consequently, many corresponding indices, such as WBGT[9], Oxford index (WD)[17], discomfort index (DI)[18], and wet-bulb dry temperature (WBDT)[19], are expressed in the format of a temperature-equivalent value or the ostensive temperature value. Most people can easily understand the thermal effect of any given temperature based on their experience. This utility may be a big reason that simple statistical indices are still the most popular. However, according to the classical heat and mass transfer theory[20], the enthalpy difference is the driving potential for the simultaneous transfer of heat and mass in an air-water/vapor mixture,i.e. sweat.

The objective of this study is to develop and validate a new index in order to assess heat stress in hot indoor environments. The index is developed based on the heat balance equation between a nude individual and the environment in which the effects of radiation can be neglected. We will show in this paper that this new heat stress index is capable of predicting the maximum allowable duration of heat exposure and physiological variables under moderate and light workloads.

1 Development of Heat Stress Index

We assumes that the nude individual works in a hot indoor environment, and the individual has a total metabolic rate. The internal wall surface temperature is close to the skin surface temperature, and the radiative heat transfer between the individual and surroundings is negligible[21]. According to the ASHRAE handbook[20], the heat balance equation of the human body per skin surface area can be written as

M-W=qsk+qres+S，

(1)

whereMis the total metabolic rate of metabolic heat production (W/m2),Wis the rate of mechanical work (W/m2),qskis the total rate of heat loss from the skin (W/m2), andqresis the total rate of heat loss through respiration (W/m2).

For most human activities,Wis very small compared with the human metabolic rate. According to the ASHRAE handbook[20],Wcan be regarded as zero.qresis also quite limited in a hot indoor environment. Therefore,qskis the key parameter that indicates the extent to which the human body removes metabolic heat and keeps heat storage below hazardous values.

For a nude individual with negligible radiative heat transfer, the heat lost from the skin dissipates to the immediate surroundings by the convection and evaporation of sweat. Hence,

qsk=C+Esk=hc(tsk-ta)+whc(Psk, S-Pa) ，

(2)

whereCis the rate of convective heat transfer from the skin (W/m2),Eskis the rate of evaporative heat loss from the skin (W/m2),hcis the convective heat transfer coefficient [W/(m2·K)],tskis the skin surface temperature (K),wis the skin wettedness dimensionless,heis the evaporative heat transfer coefficient (analogous tohc) [W/(m2·kPa)],Psk, Sis the water vapor pressure at the skin surface which is assumed to be the saturated water vapor attsk(kPa).

The Lewis ratioLcan be used to relate the surface convective and evaporative heat transfer coefficients at a low mass transfer rate. According to ASHRAE handbook[20], the Lewis ratio is about 16.5 K/kPa for typical indoor conditions.

L=he/hc=16.5.

(3)

Substituting Eq. (3) into Eq. (2), and rearranging the parameters based on the skin surface and ambient air yield

qsk=hc(tsk-ta)+16.5whc(Psk， S-Pa)=

hc[(tsk+16.5wPsk， S)-(ta+16.5wPa)].

(4)

The water vapor pressurePaof the moist air can be expressed in terms of the total or barometric pressurePtand the humidity ratio of moist aird.

(5)

wheredrefers to the humidity ratio of moist air (kg/kg).

Considering that the total pressurePtis about 101 kPa and the water vapor pressurePais always within a range of 1-5 kPa under normal indoor conditions, Eq. (5) can be simplified as

(6)

Substitute Eq. (6) into Eq. (4):

qsk=hc[(tsk+26.53wdsk， S)-(ta+26.53wda)] ，

(7)

wheredsk, Sis the humidity ratio of air at the skin surface, which is assumed as the humidity ratio of saturated moist air attsk(kg/kg);dais the humidity ratio of ambient air (kg/kg).

Enthalpy is one of the most important measures of energy in a thermodynamic system. For moist air, considering that the water vapor content is very small, the specific enthalpy of the moist air can be expressed as

H=1.006t+2 500d,

(8)

whereHrefers to the specific enthalpy of the moist air (kJ/kg).

Comparing Eq. (8) with Eq. (7) shows that the difference in the specific enthalpy plays an important role in dissipating heat from the skin surface to the surrounding air. The larger the skin wettedness is, the larger the specific enthalpy difference is. Skin wettedness is a good measure of heat stress and evaporative potential of the environment. The maximum theoretical skin moisture is 1.0, but most indoor environments need to consider the maximum safe working hours[20], and the dimensionless parameter is usually in the range of 0.5-0.8. Alber-Wallerström and Holmér[22]also studied the efficiency of sweat evaporation of six men working on a bicycle ergometer at different workloads and humidity levels, and the average skin wettedness was about 0.7. If we takew= 0.66 and insert Eq. (8) into Eq. (7),qskcan be rewritten as

qsk=hc[(tsk+1 751dsk, S)-(ta+1 751da)]≈
hc[(0.3tsk+0.7(1.006tsk+2 500dsk, S))-
(0.3ta+0.7(1.006tsk+2 500da))]=
hc[(0.3tsk+0.7Hsk)-(0.3ta+0.7Ha)],

(9)

whereHskis the specific enthalpy of air at the skin surface, which is assumed to be the specific enthalpy of saturated moist air attsk(kJ/kg).

If the individual is working in a hot indoor environment, the mean skin temperature is relatively stable, where the variation in skin temperature is always less than 2 ℃[24]. The maximum allowable duration of heat exposure is then determined based on the environmental parameters or combinations of the environmental parameters such as the WBGT index. According to Eq. (9), in an indoor environment where radiative heat transfer is negligible, the new heat stress index can be treated as the equivalent temperature based on the convective heat transfer coefficienthc. We name this new index enthalpy dry-bulb temperature (EnD) asEnD,because it is a combination of the specific enthalpy and dry-bulb temperature of the surrounding air.

EnD=0.3ta+0.7Ha.

(10)

We have devised a new rational heat stress index based on the heat balance equation between a nude individual and the environment without radiation. The mathematical expression of the EnD index is quite similar to that of the WBGT index for indoor environments. However, the difference here is that the wet-bulb temperature is replaced with the specific enthalpy. Since the EnD index is developed based on the heat balance equation between a nude individual and a typical indoor environment, this condition can be difficult to fulfil in the most situations. However, we can validate the EnD index by carrying out thermal stress tests on individuals dressed in clothing with 0.6-1.1 clo, which are quite common for indoor environments such as deep mining or submarine rooms in developing countries.

2 Validation of EnD Index

The main objective of a heat stress index is to accurately predict the maximum allowable duration of heat exposure. Many standards have recommended that the individual should be removed from the heat exposure if he/she is unable to continue working. The individual should also be removed if his/her heart rate exceeds 180 beats/min for certain time or if his/her rectal temperature reaches 39.0 ℃[24]. For these reasons, the EnD index should correlate well with key physiological variables such as the rectal temperature and the heart rate.

To validate the new EnD index, we compared the WBGT and EnD indices based on the experimental data taken from three independent studies in the scientific literature. All of these data are available publicly and used for different purposes. To eliminate variations (which were common in field experiments), all measurement data were collected in well-controlled climate chambers. It was important to note that all tests were carried out with the internal wall surface temperature close to the air temperature, not human skin temperature. However, radiative heat transfer coefficienthris nearly constant as 4.7 W/(m2·K) which is less thanhcfor the most indoor calculations[20]. According to Eq. (3), total error of ignoring radiation heat transfer can be estimated less than 6%.

2.1 Experiments based on Lind and Hellon[17]

The work of Lind and Hellon[17]was to investigate the tolerance time and physiological responses of low labor subjects in the high temperature and humidity environment. Ten healthy, and acclimatized young men were exposed to eight different indoor environments, where four were exposed to humid climates of which the dry-bulb temperature and the relative humidity were 37.0 ℃/85%, 38.0 ℃/85%, 39.0 ℃/85%, and 40.0 ℃/85%, and the remaining four were exposed to dry climates of which the dry-bulb temperature and the relative humidity were 44.7℃/45%, 46.1℃/45%, 48.9℃/45%, and 50.3℃/45%. All of the tests were carried out under conditions from which the effective temperature scale was originally developed. Therefore, the tests were carried out under the following conditions: sedentary activity (66 W/m2), light clothing (0.5-0.7 clo), and low wind velocity. The maximum duration of heat exposure was 180 min for all tests.

Figure 1 shows the comparison between WBGT and EnD indices based on the tolerance time and two physiological variables (rectal temperature in 60 min and heartbeat in 60 min). All of the experimental data were reevaluated from the work of Lind and Hellon[17]. Since not all of the subjects were able to complete the maximum duration of exposure of 180 min, and the physiological variables of each subject might be different before the subjects entered the test chamber, only the variations of the physiological variables after the first 60 min of heat exposure were compared.

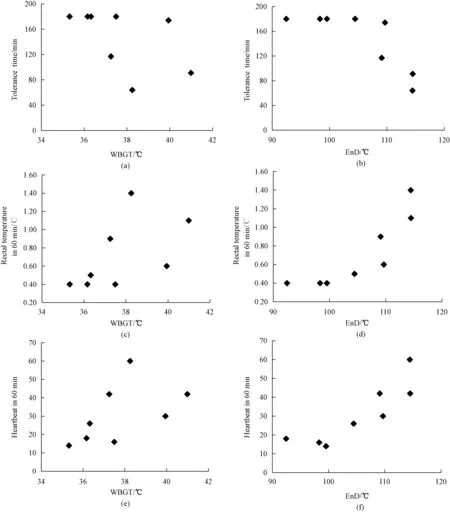
Fig. 1 Comparison between WBGT and EnD indices(low labor): (a)WBGT index based on tolerance time; (b)EnD index based on tolerance time; (c)WBGT index based on rectal temperature in 60 min; (d)EnD index based on rectal temperature in 60 min; (e)WBGT index based on heartbeat in 60 min; (f)EnD index based on heartbeat in 60 min

For the WBGT index, all of the test results fall into two distinct series based on the relative humidity (RH ≈ 85%, and RH ≈ 45%) at the start of the test. Based on the results, it is evident that the WBGT index is not an adequate measure of heat stress or physiological stress within the range of environmental conditions investigated in this study. Although there are deviations at higher EnD index values, the results obtained from the two series of climates (humid and dry climates) begin to merge into a single curve. The results indicate that it is possible to accurately assess the severity of heat stress based on the EnD index within the range of environmental conditions considered in this study. However, the deviations at higher EnD values imply that the new heat stress index still overestimates the stress imposed by the high dry-bulb temperature in severe heat. The excessive response of the WBGT index towards the dry-bulb temperature could result in significantly underestimation of heat stress in environments where the evaporation of sweat is restricted by high humidity levels or poor ventilation[29].

2.2 Experiments based on Pimental and Avellini[23]

One objective of the work of Pimental and Avellini[23]was to investigate the tolerance time and physiological responses of moderate labor subjects in an equivalent WBGT environment. Eight healthy, and well-acclimated young male subjects attempted to complete 4 h of heat exposure in five different environments. The dry-bulb temperature and the relative humidity of the five climates were 35.0 ℃/80%, 49.0 ℃/25%, 43.0 ℃/60%, 49.0 ℃/35%, and 49.0 ℃ /39%. All of the subjects wore the U.S. Navy Utility Uniform with a thermal insulation value of 1.1 clo and the wind velocity was 1 m/s. For the test, the subjects were required to walk on a level treadmill at a pace of 1.3 m/s for 25 min and then sat for 5 min every 30 min. The time-weighted metabolic rate was about 270 W(i.e., moderate labor).

Figure 2 shows the comparison between WBGT and EnD indices based on the tolerance time, rectal temperature in 60 min, and heartbeat in 60 min. All of the experimental data were reevaluated from the work of Pimental and Avellin[23]. It can be seen that the WBGT index is not a suitable predictor of heat stress for the tolerance time and physiological variables. In contrast, the EnD index shows a stronger correlation with all of variables in this case, especially for the tolerance time. Interestingly, there is a striking similarity in the patterns for rectal temperature and heartbeat between Figs. 1 and 2. We perceive that perhaps only one physiological parameter needs to be measured in the future.

Fig. 2 Comparison between WBGT and EnD indices (moderate labor): (a)WBGT index based on tolerance time; (b)EnD index based on tolerance time; (c)WBGT index based on rectal temperature in 60 min; (d)EnD index based on rectal temperature in 60 min; (e)WBGT index based on heartbeat in 60 min; (f)EnD index based on heartbeat in 60 min

2.3 Experiments based on Lü[25]

In order to develop a physiological index for heat tolerance limits in China, an artificial climatic chamber was built in Tianjin University to study the effect of heat exposure on the physiological variables in different working environments. A part of the research was well-documented in Ref.[25]. Even though the thesis was written in Chinese, the relevant data were used in the works of Refs. [26-28], which were all published in a renowned international journal.

In Lü’s study, 148 healthy young male students were tested under 45 experimental combinations. Each student only took one test to ensure that none of the subjects was acclimatized to the hot environment. All of the subjects were dressed in the same type of uniform with a thermal insulation value of 0.6 clo and the wind velocity was about 0.2 m/s. Each subject was randomly assigned to perform three levels of task: light, moderate, and heavy tasks. In order to ensure that the number of subjects was adequate as the previous two studies for statistical analysis, we only reanalyzed the results obtained for more than five subjects in one test condition. All of the cases that fulfilled this criterion could be classified as moderate workloads, where the time-weight metabolic rate was about 300 W(i.e., medium high labor).

Since the rectal temperature was not available, we only presented the comparison between WBGT and EnD indices for the tolerance time and the heartbeat in 60 min, as shown in Fig. 3. Based on the results, it is difficult to identify which index is more suitable to predict the heat stress. We perceive that the tolerance time versus the EnD index may result in better curve fitting compared with the tolerance time versus the WBGT index. However, there is a large scatter in the data points for the heartbeat for both heat stress indices. It is likely that all of the subjects are not acclimated to the heat during the tests, which leads to the large scatter of the data points.

Fig. 3 Comparison between WBGT and EnD indices(medium high labor): (a)WBGT index based on tolerance time; (b)EnD index based on tolerance time; (c)WBGT index based on heartbeat in 60 min; (d)EnD index based on heartbeat in 60 min

Epstein and Moran[3]established a compromise approach to describe the effects of environmental and behavioral factors on human thermal stress: a change of 1 clo was equivalent to a change in 10 ℃ inTawhile exercising, and a change of 0.1 m/s in air movement could be offset by 0.5 ℃ inTa. Although Lü[25], and Pimental and Avellini[23]did tests with different thermal insulation values and air speeds, the combination effect of these two factors on human stress was quite close. Considering that the results of these two studies were also obtained under a similar time-weight metabolic rate, we presented the comparison between WBGT and EnD indices for these results in Fig. 4. The most intriguing finding here is that most of the data points for tolerance time obtained from the two independent sources can be fitted into a single curve for the EnD index. This indicates the validity of the EnD index for similar work intensities.

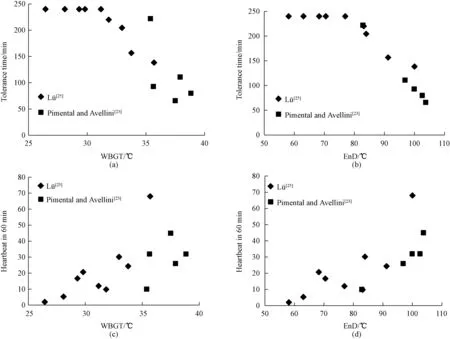
Fig. 4 Comparison between WBGT and EnD indices: (a)WBGT index based on tolerance time; (b)EnD index based on tolerance time; (c)WBGT index based on heartbeat in 60 min; (d)EnD index based on heartbeat in 60 min

3 Conclusions

In this study, the EnD index is proposed and validated against experimental data available in the scientific literature, which is derived from the heat balance equation between a nude individual and the environment in which the effects of radiation are negligible. The Lewis ratio is used to integrate evaporation of sweat with the heat lost from the skin surface to the surrounding air by convection. The EnD index can be treated as the equivalent temperature based on the convective heat transfer coefficienthc, and the EnD index is expressed as the combination of specific enthalpy and dry-bulb temperature of the surrounding air. The ratio of specific enthalpy to dry-bulb temperature is dependent on the skin wettedness.

The present EnD index is quite similar to the WBGT index for indoor environments, and the primary difference is that the wet-bulb temperature is replaced with the specific enthalpy. With this approach, the effect of dry-bulb temperature is reduced dramatically because the specific enthalpy is significantly larger than the corresponding wet-bulb temperature. The higher the water vapor content is in the air, the lower the effect of dry-bulb temperature on the EnD index is. The excessive response towards the dry-bulb temperature is indeed one of the disadvantages of the WBGT index. Theoretically, the EnD index can overcome this limitation over a wider range.

We also reevaluated the experimental data taken from three independent studies in the scientific literature in order to validate the EnD index. In all cases, it is found that the EnD index shows better correlation with the tolerance time, rectal temperature variation, and heartbeat variation after the first 60 min of the test compared with the WBGT index. In addition, the EnD index has a much wider range (50-120) compared with the WBGT index (25-40), indicating that the EnD index is more sensitive to slight changes in the environmental conditions. The EnD index is also easy to use because of its simplicity.