爆炸式催泪弹爆炸过程及刺激剂扩散特性研究

郭志勇，欧阳的华，晏皓昱，程 平

(西安建筑科技大学 资源工程学院， 西安 710055)

1 引言

爆炸式催泪弹是通过爆炸的方式将装填在其内部的刺激剂通过爆炸的方式进行快速释放，以便有效防止催泪弹被恐怖分子反投。为了评估此类弹药的作用效能和非致命特性，需要对其在起爆后，CS刺激剂云团的浓度、扩散速度等技术战术指标进行研究。近年来，国内学者对催泪弹的非致命效应进行了较多研究。欧阳的华等对自然通风条件下室内催泪剂扩散特性进行了模拟研究；何帆等通过建立基础模型研究了风速和风向对催泪弹烟雾扩散的影响；为了更好的给出催泪弹非致命效能的有效衡量方法和评价指标，王志刚等对催泪弹的气溶胶烟雾扩散过程进行了分析，并用Matlab软件编制的程序进行了仿真计算。

现有的爆炸型催泪弹一般采用将刺激剂与炸药混合的装药形式，该混装结构的爆炸型催泪弹难以满足不同作战环境和作战样式的使用需求，同时面临刺激剂选择较难、装药结构单一、刺激剂利用效率低且难以评估等问题。为此，李延等设计了一种分装结构的催泪弹，并采用高速摄影实验对其爆炸和CS刺激剂的扩散过程进行了研究。但这些研究都是针对催泪弹爆炸后的气溶胶扩散特性而展开的，而关于催泪弹弹体碎裂过程以及该碎裂过程中的CS刺激剂扩散研究尚未见报道。而其碎裂过程以及所涉及的相关参数又是后续研究的源头和基础，且该过程中所涉及的弹体快速碎裂和刺激剂的浓度变化等，目前还尚未有较为准确的测试方法，所以对此进行模拟研究具有重要的实际意义。

AUTODYN是一个显式有限元分析程序，可用来解决固体、流体、气体及其相互作用的高度非线性动力学问题，该软件在处理爆炸及其后续过程问题上具有高效、灵活、易用等显著优势。通过仿真模拟可以得到爆炸初期催泪弹整体的结构变化，更好地分析扩散走势以及原因，并且不受实验条件的制约，能够较好的弥补实验测试的不足。

为此，本文以分装结构装药的爆炸式催泪弹为研究对象，采用AUTODYN软件，对弹体碎裂过程进行了仿真，在此基础上，对爆炸型催泪弹气溶胶扩散特性进行了模拟，并将模拟结果与实验结果进行了对比验证，以期为后续CS扩散特性的仿真计算提供初始参数，同时也可为爆炸式催泪弹的安全性与作用效能的评估奠定基础。

2 仿真模拟模型

2.1 模型建立

为了验证本文研究结果的准确性，本文采用文献[10]的实验结果进行对比，按照1∶1的比例构建仿真模型，如图1所示。由文献[10]可知，图1中的青色部分是聚乳酸(PLA)外壳，厚度为2.3 mm，高度为76.5 mm；红色部分为CS刺激剂药柱，厚度为14.072 mm，高度为60 mm；黑色部分为钝化黑索金，厚度为3.178 mm，直径12.2 mm，高度为58.6 mm；空白处部分空间为起爆点，采用8号电雷管进行起爆。

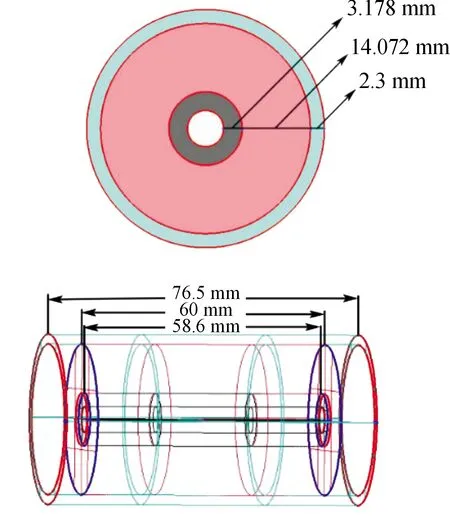
图1 分装结构模型示意图

网格生成是计算流体力学数值计算中的重要一环。物理模型创建好后，采用六面体结构对其进行网格划分。由于爆炸接触面及刺激剂药柱是此次模拟的要点，需要对其进行细化加密处理。同时根据模型参数，设置最大尺寸为1 mm，最小尺寸为0.5 mm，生成网格，如图2。共生成 112 956个六面体网格，检查网格质量良好。

图2 网格模型示意图

2.2 算法选择

划分网格结束后将模型导入AUTODYN中。由于关注的是粒子扩散过程，所以炸药、刺激药剂和聚乳酸外壳将采用SPH(smoothed particle hydrodynamics)算法。SPH算法是一种流体模拟算法，它的特点是简单快速。同时，SPH算法是典型的拉格朗日视角，其基本原理就是通过粒子模拟流体运动规律，然后再转换成网格进行流体渲染。

方法第一步是核函数近似，关于位置矢量的任意函数()在求解域中可表示成积分形式：

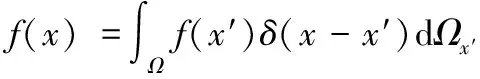
(1)

式中，(-′)是狄拉克函数，具有如下特性：

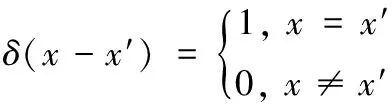
(2)

如果使用函数(-′，)代替狄拉克函数，则()的积分表达式可以近似表示为：

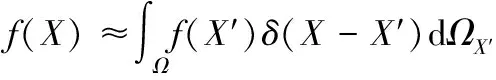
(3)

式中，(-′，)被称为核函数(Kernel function)或光滑函数(Smoothingfunction)，它是关于位置矢量和光滑长度的函数。在SPH方法中，通常用角括弧表示核估计：

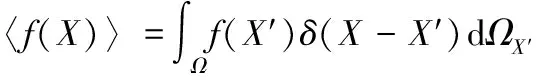
(4)

因此，式(4)就是核函数近似的标准表达式。因为核函数定义了粒子影响域的大小，决定了计算的精度和效率，在SPH方法中具有十分重要的作用。

SPH方法第二步是粒子近似。在SPH方法的实际求解过程中，求解域由一系列任意分布的粒子离散而成，因此任意点处函数及其导数的核函数近似积分表达式需要转化为其影响域内所有粒子场函数叠加求和的形式，这就是粒子近似的思想。

2.3 材料模型

选定算法后，假设空气、炸药均为连续介质，空气为理想气体，并设置重力加速为轴-9.8 m/s。空气采用无粘性理想气体和线性多项式状态方程，地面采用刚性地面。

空气状态方程为：

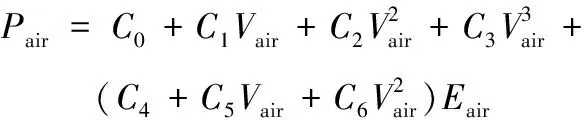
(5)

式中：为空气的压力；为相对体积；为空气单位体积内能，=2.068×10J·kg；=0.1 MPa，====0，==0.4，空气密度取1.29×10g·cm。

炸药爆轰产物的压力可用JWL状态方程来描述：

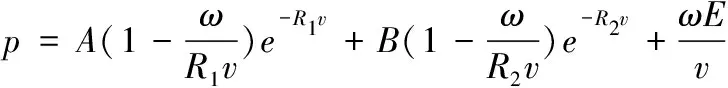
(6)

式中：为单位质量内能；为比容；为爆轰压力；、、、、为常数。COMP B黑索金炸药爆轰产物的JWL状态方程参数，如表1所示。

表1 JWL状态方程参数值

刺激剂药柱以及聚乳酸外壳均为自定义材料，采用Bilinear Harder强度模型。材料的应力-应变关系式为：

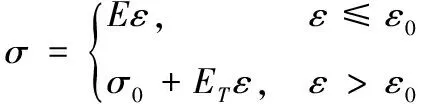
(7)

式中：、分别为材料达到屈服极限时所对应的应力和应变值；为切线模量。

从材料库选定炸药材料COMP B聚黑索金。由于针对的是地爆条件，所以从材料库中选择混凝土材料CONC140MPA作为起爆地面，并对模型外壳底部以及地面实施固定约束，假设混凝土地面刚性很大不发生破裂形变。同时对刺激药柱及外壳进行强度、断裂系数、泊松比等相关参数的设置。每隔0.1 ms保存一次数据。

3 结果与分析

3.1 爆炸过程的初始特性

图3(a)为文献[10]的高速摄影实验结果，将模拟结果[如图3(b)所示]与其进行对比验证。由图3(b)可知，模拟初期，装药引爆后在模型内部形成类球状的冲击波，使模型从轴向与径向破裂。经过一段时间后，可以看到模拟的爆炸扩散过程大致分为2个部分：上、下两端伞状扩散部分。上端边缘部分收到空气阻力以及湍流流动的影响开始伞状滚动扩散；底端部分受地面约束的控制加速向外扩散，呈现扁平状。刺激剂扩散受地面的影响较大，加速阶段较为短暂。

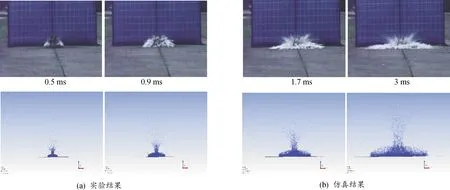
图3 爆炸产物扩散高速摄影结果(a)和模拟结果(b)示意图

同时，由于地面约束，云团在触碰到地面后直径迅速增大，远远大于上端部分，从而导致“类瓶颈”状出现。随后云团直径不断变大，大约在3.1～3.5 ms后，进入减速状态，云团直径增速变缓。通过图3(a)和图3(b)的对比可知，在实验爆炸中上端同样出现尖刺型伞状扩散，但在底端扩散呈现不规则状，与模拟中底部回卷滚动扩散略有不同，但总体吻合较好。

3.2 云团直径、高度对比

取0～30 ms的模拟数据与文献[9]实验结果相对比，发现模拟结果中云团直径、高度要大于实验云团直径、高度。这是因为软件模拟中，在考虑到湍流空气阻力后，模拟环境处于理想化状态，同时实验数据在后续测量中会存在一定误差。通过图4、图5可以看出，模拟曲线在3 ms附近出现拐点，与3.1节中分析的“在3 ms左右阶段进入减速阶段”相验证；在10.2 ms后，曲线处于平缓上升趋势。

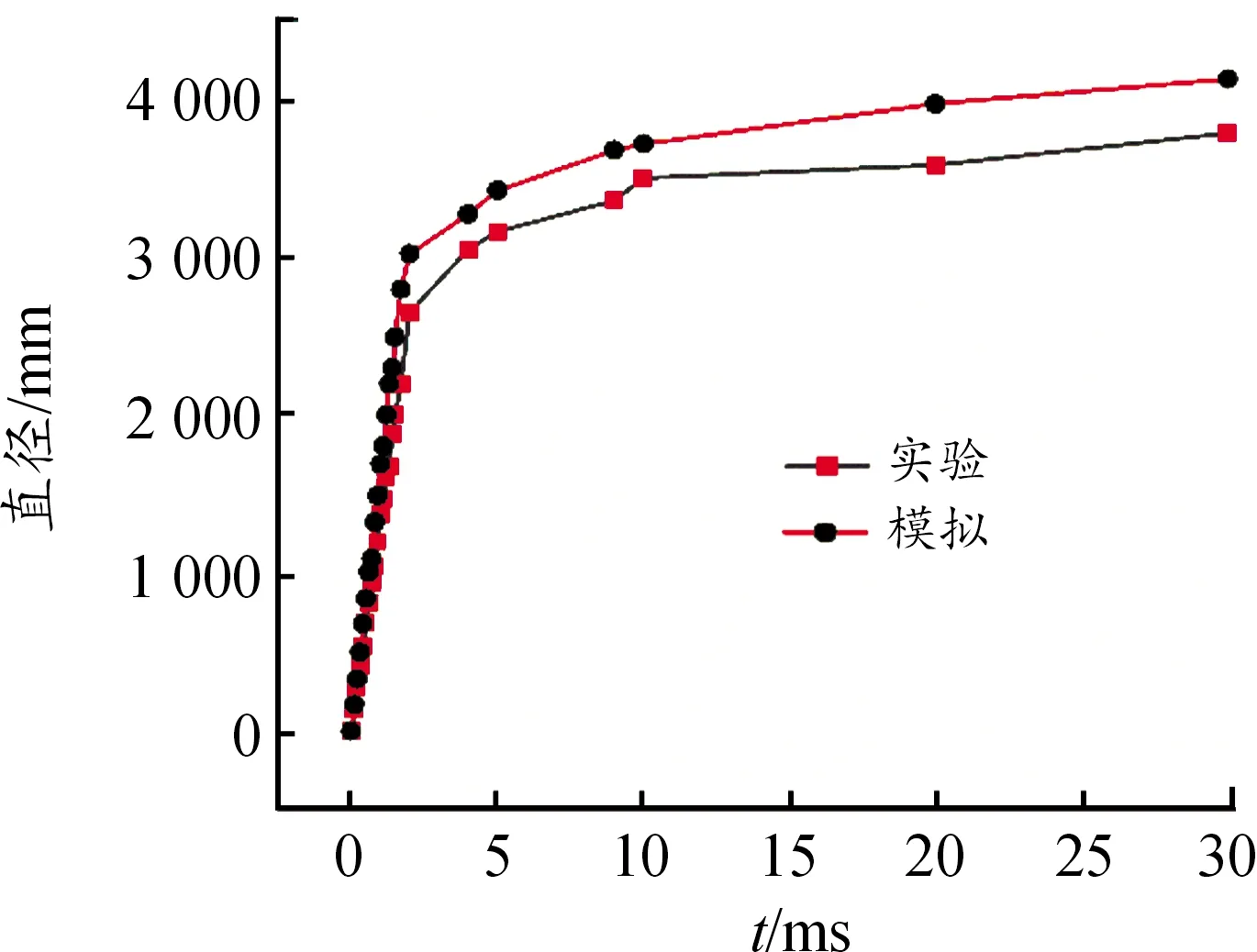
图4 云团直径曲线

图5 云团高度曲线

3.3 刺激剂云团速度分析

除去极端粒子，隐去模型外壳，分析各时间段刺激剂云团速度可知：在顶部与底部为刺激剂云团扩散速度较大区域。在0.5至08 ms 时间段内，刺激剂云团经历了加速阶段速度最大值，最大值区间为[1 304，1 562]m/s。与实际实验结果0.7 ms地爆时达到最大速度1 495 m/s比较吻合，如图6。在爆炸初期，由于引爆位置的不同，距离起爆药最近的部分先炸裂从上下两端散出，爆轰波沿着模型向上、下传递，此时模型外壳和CS刺激剂药柱还没有完全分解，如图7所示。随后，便形成图6中速度云团略低的蓝色部分。

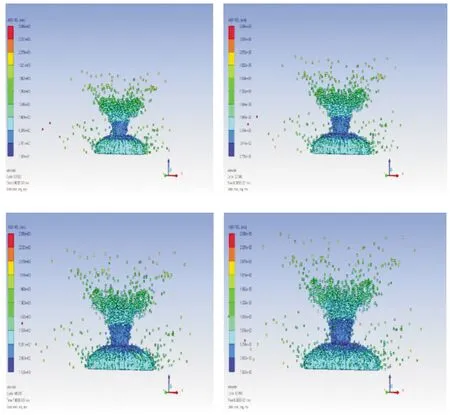
图6 0.5～0.8 ms刺激剂云团速度云图

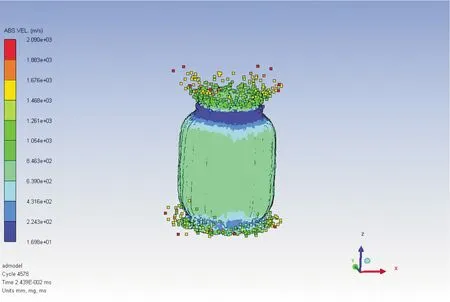
图7 爆炸初期的刺激剂分布云图

4 结论

1) 实验结果与模拟结果有较高的吻合度。模拟中爆炸产物呈现两端伞状扩散并受空气阻力及湍流流动影响回卷滚动，与实验样弹爆炸后扩散形状、规律基本相同，验证了利用该软件进行爆炸型催泪弹气溶胶扩散模拟的可行性。

2) 在地爆条件下，刺激剂云团扩散受地面环境影响较大，加速阶段较为短暂，在0.5至0.8 ms 时间段内，刺激剂云团经历了加速阶段速度最大值，最大值区间为[1 304，1 562]m/s。与实验结果对比发现，不同的速度峰值最终导致云团直径、云团高度产生差距。速度的变化是导致后续云团变化的重要指标。