多传感器异步信息多源组合导航算法实现

赵海飞,陈 帅,刘清秀,廖泽俣,马永犇

（南京理工大学自动化学院,南京 210094)

0 引言

目前,导航领域的研究以组合导航为主,尤其是以惯性导航为基的多源组合导航。联邦Kalman滤波要求各个传感器的量测信息同时到达[1],但是多源组合导航系统中传感器数量和种类较多,各传感器的采样率存在差异,导致各子滤波器的量测周期不同,即异质传感器异步信息的不等间隔问题,影响了系统的导航精度[2]。

秦永元等[3-4]设计了一种经典的异步信息融合方法,利用时间更新将来自不同传感器的异步信息进行同步。刘丽丽等[5]基于多尺度模型设计了一种多传感器组合导航系统,将异步融合算法分为时间序贯过程和传感器量测序惯过程,仿真结果证明了该算法的高精度性和可行性,但是该算法计算量大,工程实现困难。王宏等[6]设计了一种异步联邦无迹Kalman滤波器（Unscented Kalman Filter,UKF),将滤波器中的时间更新与量测更新分离,以此来解决全球导航卫星系统（Global Navigation Satellite System,GNSS)/捷联惯性导航系统（Strapdown Inertial Navigation System,SINS)/摄影测量（Photogrammetry)组合导航系统测量量测信息不等间隔问题。

本文简化了文献[6]的算法,设计了一种异质传感器异步信息非等间隔滤波算法,以INS/GNSS/高度计/磁强计组合导航系统为例,通过半物理仿真实验验证了该算法的可行性和导航精度,并将其移植到嵌入式平台,通过跑车实验证明该算法能够工程实现,有较高的工程应用价值。

1 联邦滤波器设计

Kalman滤波主要分为集中式Kalman滤波与分布式Kalman滤波两种方式。集中式Kalman滤波虽然能够得到对状态的最优估计,但由于传感器种类的增加以及滤波状态维数的增大,使得集中式Kalman滤波的计算负担和通信负担加重,不易于工程实现[7]。此外,当某个导航传感器发生故障而导致其导航精度下降甚至发散时,集中式Kalman滤波的结构特性使得系统无法对故障信息源进行检测与隔离,系统导航结果整体精度也会随之下降,系统的容错性能差。为了解决以上问题,Carlson于1988年提出了联邦Kalman滤波（Federated Kalman Filtering)。相对于集中式Kalman滤波,联邦Kalman滤波降低了算法的复杂性、提高了容错性和可靠性,并且设计灵活,便于工程实现,受到了广泛的重视[8-9]。

联邦Kalman滤波是一种具有两级结构的分布式Kamlan滤波,该滤波算法由若干个子滤波器和一个主滤波器组成,其结构如图1所示。

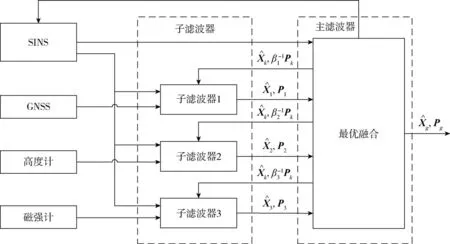
图1 联邦滤波结构示意图Fig.1 Structure diagram of federated filtering

1.1 系统状态方程

系统的状态方程为

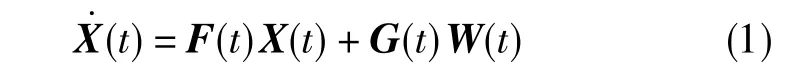
式（1)中,X（t)为由SINS误差变量构成的18维状态向量,F（t)为系统的状态转移矩阵,G（t)为系统的噪声驱动矩阵,W（t)为系统的噪声随机误差向量。

系统的状态向量设计为

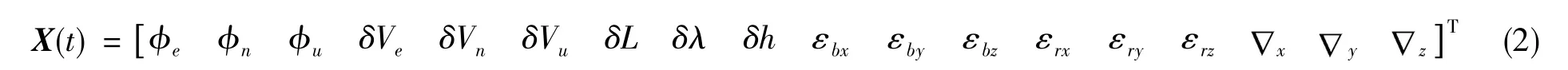
式（2)中, ϕe、 ϕn、 ϕu分别为捷联式惯性导航系统在东向、北向、天向上的姿态角误差,δVe、δVn、δVu分别为捷联式惯性导航系统在东向、北向、天向上的速度误差,δL、δλ、δh分别为捷联式惯性导航系统在纬度、经度、高度上的位置误差, εbx、 εby、 εbz分别为陀螺仪在 x、 y、 z三个轴向上的随机常值误差,εrx、εry、εrz分别为陀螺仪在x、y、z三个轴向上的一阶 Markov偏移误差,、、分别为加速度计在x、y、z三个轴向上的一阶Markov偏移误差[10]。

1.2 量测方程

子滤波器1将SINS输出的位置、速度量测值与GPS输出的位置、速度量测值作差作为系统量测向量,系统量测方程为

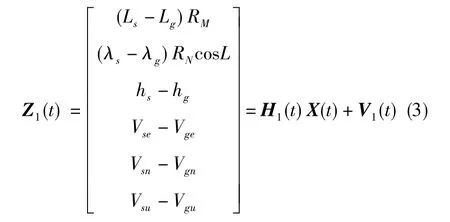
式（3)中,Ls、 λs、 hs为 SINS 输出的纬度、 经度、高度信息,Vse、Vsn、Vsu为SINS输出的地理系下载体在 x、y、z三个轴向上的速度信息,Lg、λg、hg为 GNSS输出的纬度、经度、高度信息,Vge、Vgn、Vgu为 GNSS输出的地理系下载体在 x、y、z三个轴向上的速度信息,H1（t)为量测矩阵,V1（t)为量测噪声。

子滤波器2将SINS输出的高度量测值与高度计输出的高度量测值作差作为系统量测向量,系统量测方程为

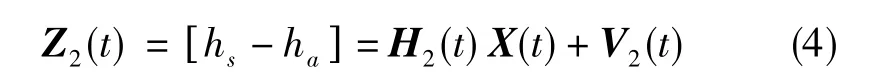
式（4)中,ha为高度计输出的高度信息,H2（t)为量测矩阵,V2（t)为量测噪声。

子滤波器3将SINS输出的航向角量测值与磁强计输出的航向角量测值作差作为系统量测向量,系统量测方程为

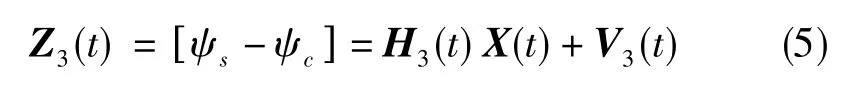
式（5)中,ψs为 SINS输出的航向角信息,ψc为磁强计输出的航向角信息,H3（t)为量测矩阵,V3（t)为量测噪声。

1.3 主滤波器信息融合

主滤波器将各子滤波器的滤波结果进行融合,融合方法如下

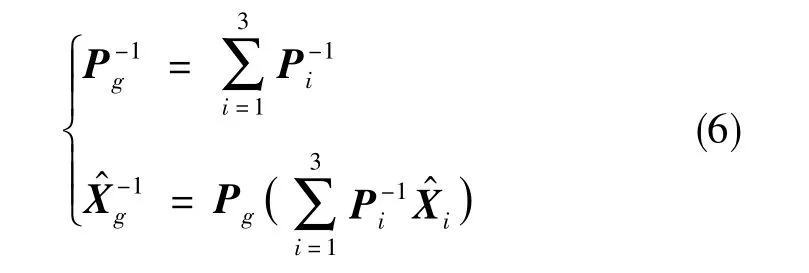
式（6)中,Pg、为主滤波器输出的最优方差阵和全局最优估计。

2 异质异步非等间隔信息处理

2.1 算法设计

首先,分离Kalman滤波器中的时间更新和量测更新。时间更新为

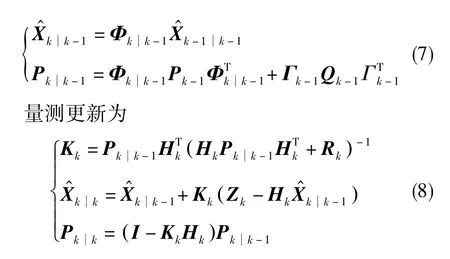
设第 i个传感器的量测周期为 Ti（i=1,2,3,…,m),主滤波器的计算周期为Tc,融合周期为Tf,Tc和Tf定义如下

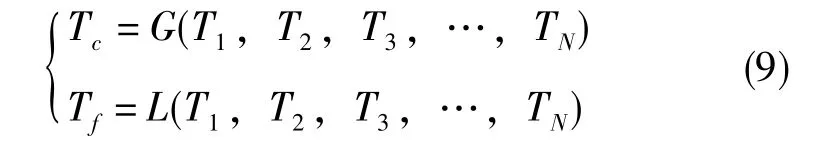
式（9)中,G（·)表示求取最大公约数,L（·)表示求取最小公倍数。定义m为各计算周期Tc划分的时间刻度,有Ti=miTc（mi为互质的自然数)。当各子滤波器同时有量测更新时,即Tf=Tc时,完全满足联邦Kalman滤波算法要求;否则,设计如下算法:

（1)对子滤波器

当m=mp时,即此时主滤波器有量测更新时

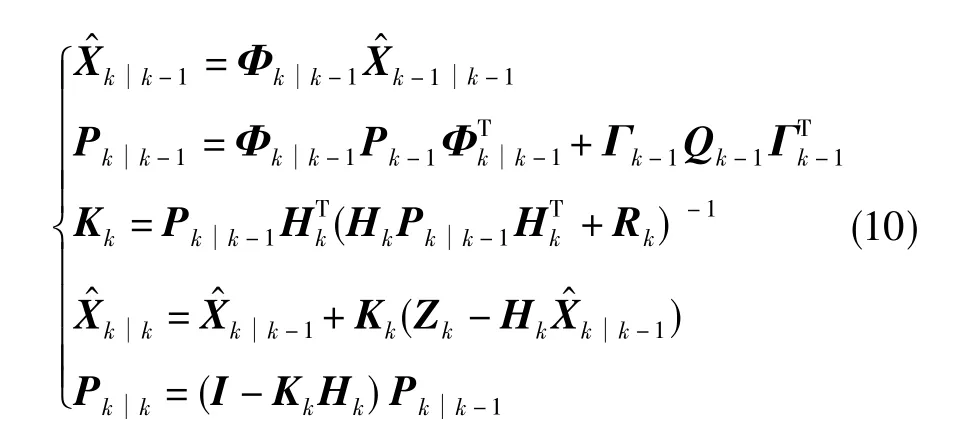
当m≠mp时,即此时主滤波器没有量测更新时,子滤波器只进行式（7)的时间更新。

（2)对主滤波器

当Tf=Tc,即此时主滤波器有量测更新时,主滤波器进行式（6)的信息融合;当Tf≠Tc时,即此时主滤波器没有量测更新时,此时主滤波器不进行任何操作。

其中,mp为子滤波器有新的量测更新的时刻,如果当前子滤波器没有新的量测信息时,即满足m≠mp时,子滤波器只进行时间更新;如果当前子滤波器有新的量测信息时,即满足m=mp,子滤波器同时进行时间更新和量测更新。对于主滤波器,只有当主滤波器有量测更新时,主滤波器进行信息分配。

2.2 嵌入式平台搭建

本文选择国产自主研发设计制造的MIMU（微型惯性测量单元)模块、北斗导航计算机和芯片原子钟深度集成一体化,通过串口与上位机实现通信,实时查看导航结果并保存数据。其中,MIMU模块陀螺仪零偏稳定性≤3（°)/h,加速度计零偏稳定性≤0.25mg,原子钟1pps同步精度优于±50ns,外秒驯服精度等级和频率调节范围等级分别可达5×10-12和1×10-6,原子钟将BDS导航计算机解算出的1pps信号进行同步驯服,并输出驯服后的1pps信号为外界用户提供授时服务。外源传感器选择低成本气压高度计和磁强计,通过CAN总线接入嵌入式平台实现即插即用。

3 仿真校验

为了验证所述的异质异步非等间隔信息处理算法在实际工程应用中的可靠性和有效性,本文设计了半物理仿真实验。通过实际跑车采集MIMU、北斗卫星接收机、高度计和磁强计的数据进行离线仿真,并与SPAN-KVH1750高精度组合导航系统采集的基准数据进行比较。跑车实验初始位置为北纬32.016047°、东经118.889261°,高度为7m,寻北结果为-24.633°。设备装车效果图如图2所示,跑车行驶路线如图3所示。

图2 设备装车效果图Fig.2 Effect diagram of equipment loading

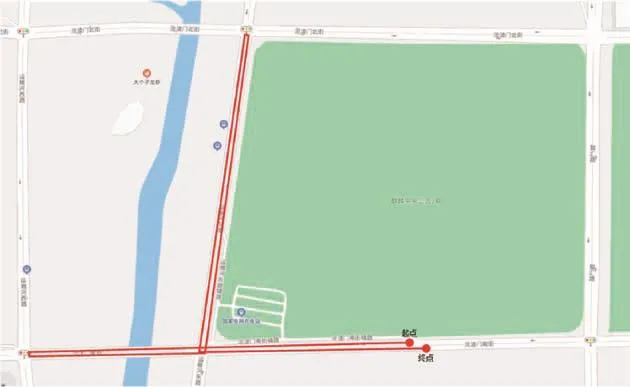
图3 跑车实验行驶路线Fig.3 Driving route of vehicle experiment

上述设备的性能指标如表1所示。

由表1可知,实验所用传感器输出频率各不相同,必然会导致异质传感器异步信息的不等间隔问题。

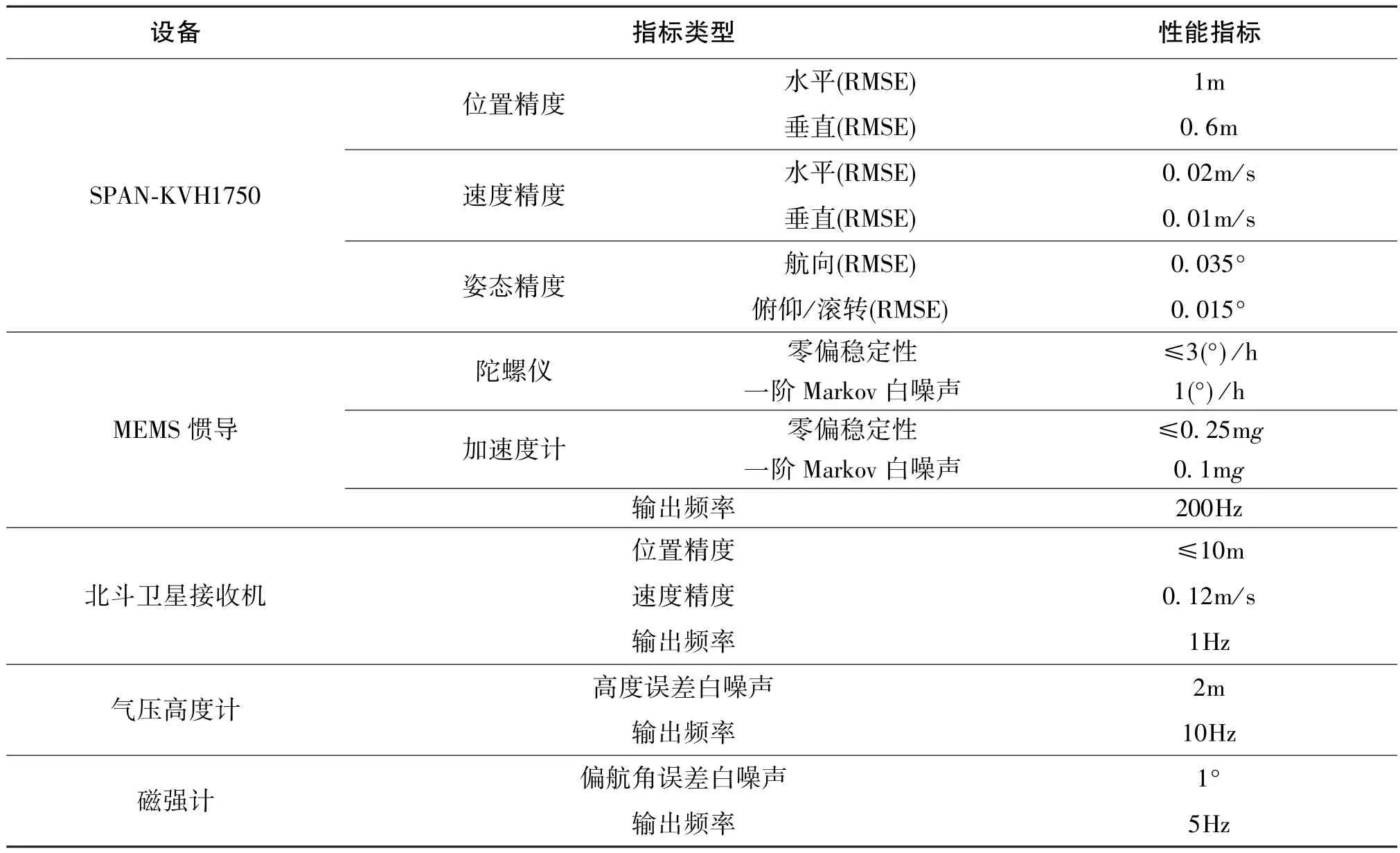
表1 实验设备性能指标Table 1 Performance indicators of test equipment

跑车时长为300s,得到的数据通过上位机监控存入计算机,然后分别进行异质异步非等间隔信息处理算法和传统分散式联邦滤波算法数据融合离线仿真,通过与高精度基准对比得出误差,两者的误差对比曲线如图4、图5所示。

实验过程中为保证本文算法正常运行,数据处理时截取了车辆行驶过程中各传感器均正常工作时的一段数据,剔除了传感器故障时的数据（如卫导丢星、PDOP值过高等),故导致部分方向上初始误差不同。由图4可知,使用联邦滤波算法时,经计算得到的东向速度的均方根误差为0.1272m/s,北向速度的均方根误差为0.1300m/s,天向速度的均方根误差为0.1013m/s;使用非等间隔信息处理算法后,经计算得到的东向速度的均方根误差为0.0939m/s,北向速度的均方根误差为0.0919m/s,天向速度的均方根误差为0.0930m/s,东北天速度精度分别提升了26.2%、29.3%和8.2%。由图5可知,使用联邦滤波算法时,经计算得到的纬度方向的均方根误差为2.1193m,经度方向的均方根误差为4.3058m,高度方向的均方根误差为6.2032m;使用非等间隔信息处理算法后,经计算得到的纬度方向的均方根误差为1.3842m,经度方向的均方根误差为3.3030m,高度方向的均方根误差为5.4140m,东北天位置精度分别提升了34.7%、23.3%和12.7%。

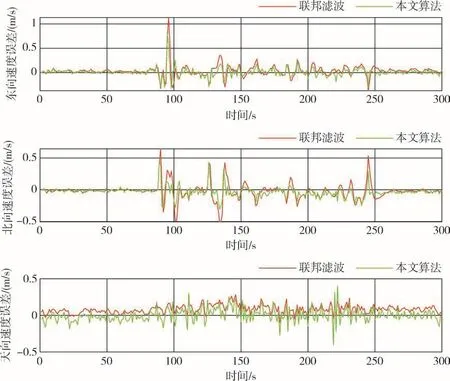
图4 速度误差对比曲线Fig.4 Comparison curves of velocity error

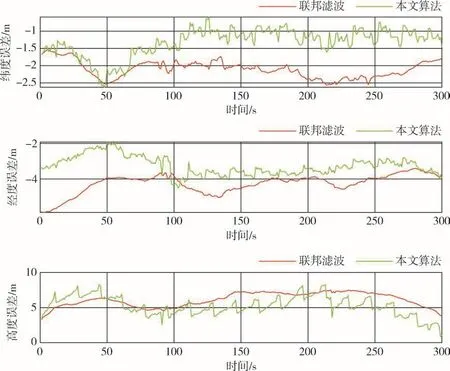
图5 位置误差对比曲线Fig.5 Comparison curves of position error

上述仿真结果表明,添加非等间隔信息处理后确实能够提高导航性能,输出更加精确、可靠的导航结果。

4 跑车实验

图6为跑车实验路线图,跑车初始位置与初始航向设置与仿真校验相同,设备装车效果和设备性能指标也和仿真校验一致（图2和表1)。

图6 跑车实验路线图Fig.6 Roadmap of vehicle experiment

本次跑车实验先给导航板上电正常启动,等待至接收机定位且进入组合导航阶段,输出稳定后启动车辆进行跑车测试。本次测试选用NovAtel-KVH1750作为参考系统,测试得到的数据与其进行速度、位置对比,结果如图7、图8所示。

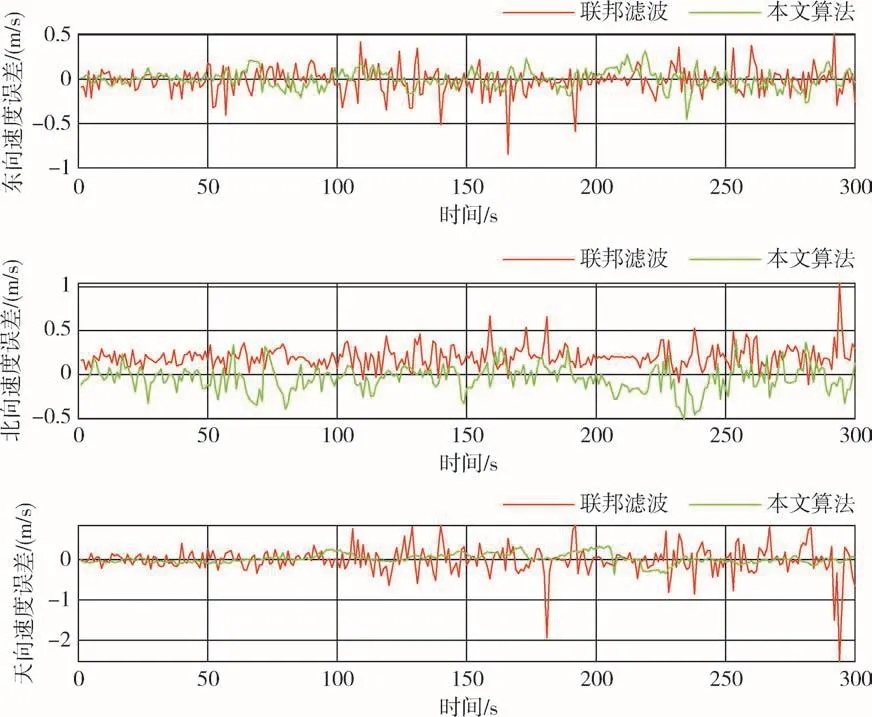
图7 速度误差对比结果Fig.7 Comparison results of velocity error

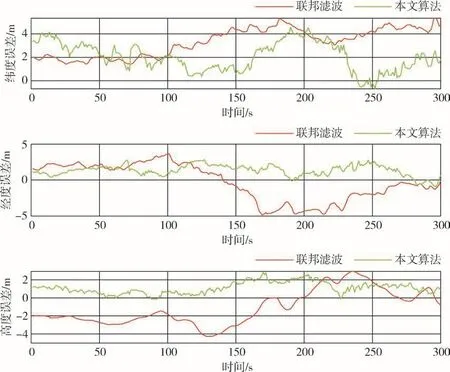
图8 位置误差对比结果Fig.8 Comparison results of position error

实验过程中,部分方向上初始误差不同是因为截取了各传感器均正常工作时的一段数据。由图7可知,使用联邦滤波算法时,经计算得到的东向速度的均方根误差为0.1461m/s,北向速度的均方根误差为0.2355m/s,天向速度的均方根误差为0.3399m/s;使用非等间隔信息处理算法后,经计算得到的东向速度的均方根误差为0.1007m/s,北向速度的均方根误差为0.1544m/s,天向速度的均方根误差为0.1201m/s,东北天速度精度分别提升了31.1%、34.4%和64.6%。由图8可知,使用联邦滤波算法时,经计算得到的纬度方向的均方根误差为3.5225m,经度方向的均方根误差为2.5570m,高度方向的均方根误差为2.1985m;使用非等间隔信息处理算法后,经计算得到的纬度方向的均方根误差为2.3899m,经度方向的均方根误差为1.5371m,高度方向的均方根误差为1.2726m,东北天位置精度分别提升了32.2%、39.9%和42.1%。

由跑车实验测试结果可知,加入非等间隔滤波算法后,位置精度和速度精度都有较大提升,证明了异质异步非等间隔信息处理算法切实有效,应用于组合导航算法后能有效提高导航精度,具有较高的工程应用价值。

5 结论

本文详细介绍了异质异步非等间隔信息处理算法,通过将Kalman滤波的时间更新和量测更新分离,有效解决了不等间隔问题。以车载SINS/GNSS/高度计/磁强计多源组合导航系统为实验对象,分别进行了半物理仿真和跑车实验。实验结果表明,异质异步非等间隔信息处理算法在多源组合导航系统中能够解决不同传感器量测信息不同步的问题,有效提高了系统位置精度和速度精度。该算法可以应用到工程实践中,具有很高的应用价值。