群论解决计数问题的一个教学改进
王丽杰, 王庆先
(1.电子科技大学 计算机科学与工程学院,成都611731;2.电子科技大学 信息与软件工程学院,成都610054)
1 引 言
群论是近世代数中非常重要的理论,渗入现代数学、物理、化学和计算机等学科的方方面面[1-4].例如,可应用群论解决一般情况下难以求解的计数问题,包含项链问题、正多面体着色问题、图和开关电路的同构计数问题等[5].对于这些计数问题的求解,现有的近世代数教材都是先讲解群对集合的作用和轨道这两个概念,再推导伯恩赛德引理,最后再利用伯恩赛德引理来解决特定的计数问题[5-6].有的教材甚至完全没有讲到计数问题的求解[7-8].这些概念定理都很晦涩难懂,因而学生理解起来非常困难.在本科阶段,考虑到难度,离散数学教材一般会直接省略这部分内容.但是,群论本身已经是很抽象的理论,如果能够在教学过程中引入利用群论解决计数问题的实际应用,让学生体会到群论的魅力,可有效的提升教学体验.因而,本文讨论直接利用置换群知识解决一种典型的计数问题——项链问题,然后可将其引申到伯恩赛德定理.这样,学生可在缺少相关理论基础,仅学习了置换群的情况下理解计数问题的求解思路.而需要进一步学习的学生,也能够对于群对集合的作用和轨道两个概念有更加形象直观的认识,对于理解和运用伯恩赛德定理解决类似的计数问题会有非常大的好处,从而形成教学逻辑的平滑过渡.
2 项链问题及二面体群描述
项链问题可形象的描述为,用n种颜色的珠子做成有m颗珠子的项链,问可做成多少种本质上不同的项链?
首先将这个问题转化为数学形式.m颗珠子做成一个项链,可用一个正m边形来表示,每个顶点代表一颗珠子.从任意一个顶点开始,沿逆时针方向,每个顶点用1,2,…,m来标号.这样的一个有标号项链中,每一颗珠子有n种选择,所以总共有nm种.但是,有一些其实本质上是一样的,比如旋转一个角度或者翻转后就会重合.若只考虑本质上不同的项链,当n和m数值较大时,则很难用简单的枚举方法来解决.群论方法是当前解决这一类问题最为简单和有效的方法,即利用二面体群来求解.
考虑正m边形在三维空间中保持各顶点相对位置不变的旋转或翻转变换,可简称RFT(Rotate-Flip Transformation).每个RFT对应其顶点集合的一个置换,两个置换的乘积就是一个RFT接着另一个RFT,一个RFT的逆就是其反向RFT,因此,所有RFT构成一个群,这个群是m次对称群Sm的子群,也是一个置换群,通常称为二面体群,记为Dm.
接下来给出二面体群Dm的一般表达形式.设X={1,2,…,m}为正m正边形的顶点集合,且按逆时针方向排列,如图1所示.

图1 正m边形的变换
正m边形有两种旋转方式:绕中心O沿逆时针方向旋转和关于一条对称轴进行翻转.
将正多边形绕中心O沿逆时针方向旋转2kπ/m度(k=0,1,2,…,m-1),则得到m个变换,可用轮换表示为
ρk=(1 2 3 …m)k,k=0,1,…,m-1,
而若将正多边形绕图1所示的对称轴l0,l1,…,lm-1翻转角度π,同样得到m个变换,使用轮换表示为
π0=(2m)(3m-1)…,
πk=π0ρk,k=0,1,2,…,m-1,
因此,二面体群可表示为
Dm={ρk,πk|k=0,1,2,…,m-1}.

3 仅利用置换群知识解决项链问题
首先假设集合Ω={a1,a2,a3,…}表示所有项链样式的集合,即|Ω|=nm.每个项链样式经过二面体群Dm中的任何一种置换后可变换成另一种样式,可用数学形式描述为
∀ai∈Ω,g∈Dm, ∃aj∈Ω,g(ai)=aj.
设Ω中本质上不同的项链有N种,由于每一种样式都有2m种方式进行变换,可选择其中任何一个作为代表样式,记为Δ={b1,b2,…,bN},显然Δ⊂Ω.


图2 项链样式的变换
显然,可得到如下事实:
事实1C11,C12,…,CN(2m)包含了Ω中所有元素.
证显然成立,否则Δ={b1,b2,…,bN}不能包含所有本质上不同的项链样式.
事实2当i≠j,则Mi与Mj不相交,即Mi∩Mj=∅.
证反证法.假设Mi∩Mj≠∅,即∃x∈Mi∩Mj,所以∃g,h∈Dm,使得g(bi)=x,h(bj)=x.由于i≠j,即有bi和bj本质上不同.但x=g(bi)=h(bj),可见bi=g-1h(bj),这说明bj经过置换g-1h变换之后成为bi,可见bi∈Mj,这说明bi和bj本质上是相同的.出现矛盾,事实2得证.
由事实1及图2,可知:对∀ai∈Ω,∃g∈Dm,bj∈Δ,使得g(bj)=ai.其中i∈{1,2,3,…,nm},j∈{1,2,3,…,N}.此时令集合Bij={g|g∈Dm,g(bj)=ai},这里j取值是特定的.易知Bij≠∅.又由事实2,得到ni=|Bij|.而为了求出|Bij|,需要引入下面的事实3和事实4.
事实3令Ai={g|g∈Dm,g(ai)=ai},i∈{1,2,3,…,nm},则Ai是Dm的一个子群.
证Dm有单位元ρ0,ρ0表示逆时针旋转0度,即ρ0(ai)=ai,从而ρ0∈Ai.又对∀g,h∈Ai,则有g(ai)=ai,h(ai)=ai,即gh-1(ai)=ai,从而gh-1∈Ai.所以,Ai是Dm的一个子群.
事实4|Ai|=|Bij|,i∈{1,2,3,…,nm},j∈{1,2,3,…,N}.
证可通过在Ai和Bij之间建立一个双射来证明.根据事实3,Ai是Dm的一个子群,从而有单位元ρ0∈Ai.由于Bij≠∅,因此必然存在某一置换g∈Bij,使得g(bj)=ai.
建立映射f∶Ai→Bij,对于∀h∈Ai,令f(h)=hg.由于hg(bj)=h(g(bj))=h(ai)=ai,所以hg∈Bij.根据群的消去律,可知f是单射.又对∀δ∈Bij,由于δ(bj)=ai,g-1(ai)=bj,可知δg-1(ai)=δ(g-1(ai))=δ(bj)=ai.从而∃δg-1∈Ai,使得f(δg-1)=δg-1g=δ.即f是满射.所以,f是Ai到Bij的双射,从而|Ai|=|Bij|.
|Ai|直观上表示的是对项链样式ai进行变换后仍然得到ai的置换数量.考虑如下函数:ψ:Ω×Dm→{0,1},对

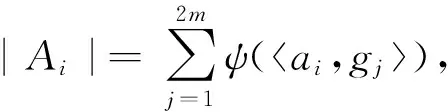
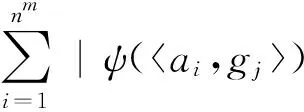


根据以上推导,得到项链问题的最终解法.本质上不同的项链个数为

例1用3种颜色做成有6颗珠子的项链,可做多少种不同的项链?
解这里n=3,m=6, 对应二面体群为D6.D6中有12个元素,ρ0是16型,ρ1和ρ5是61型,ρ2和ρ4是32型,ρ3是23型,πk(k=0,1,…,5)则有3个1222型及3个23型.所以总共有1个16型置换,3个1222型置换,4个23型置换,2个32型置换,2个61型置换.从而
即总共有92种本质上不同的项链.
综上,基于置换群给出了项链问题的解法.
4 伯恩赛德引理的引申
对于伯恩赛德引理有进一步学习需求的学生,也可在理解了上面的项链问题解法之后,引申出群对集合的作用及轨道相关的概念,并得到伯恩赛德引理.表1给出相关概念定理的对应关系.

表1 伯恩赛德引理相关概念的对应
5 结 论
本文提供了计数问题的低难度解法,使得教师可在不引入群对集合的作用和轨道两个概念及伯恩赛德定理的情况下讲解群论的实际应用,增加课堂趣味性和有效性.同时,还可以更顺利的引入这些重要但抽象的概念和定理,从而提升教学体验.作者已在近世代数和离散数学课堂讲授中应用了这些思路,取得了较好的教学效果.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

