探案式教学的探索与实践
——以微分几何伪球面为例
苏永美, 刘白羽, 范玉妹
(北京科技大学 数理学院,北京100083)
1 引 言
当今时代,大国博弈,竞争激烈,而国家之间的竞争最终会体现在科技水平的竞争,科技水平的高低取决于国家人才的质量,本科教育在一个国家的人才培养中有着举足轻重的作用.我们国家历来重视本科教学,2018年6月21日,教育部组书记、部长陈宝生在新时代全国高等学校本科教育工作会议上的讲话,2019年10月8日,教育部下发的深化本科教学改革的具体指导意见,2020年10月27日教育部高等教育司联合中国高等教育学会举办的首届全国高校教师教学创新大赛,这体现了国家对本科教学的高度重视.
大学数学教学对理工科创新型人才培养具有先导性、全局性、基础性地位[1],培养学生数学思维创新能力、数学理解创新能力、数学应用创新能力一直是大学数学教学所追求的高要求、高目标[2].但一个不容忽视的现状是,目前高校中理工科的数学类基础课教学,相当一部分还是传统的大班授课,讲授法作为基本教学方法的地位也不容小觑[3].在这种情况下,在传统课堂的基础上,教学内容的呈现、教学模式的设计、教学手段的使用如何进行创新,学生在教师的引导下充分参与到课堂中来,真正实现师生互动、生生互动,传统课堂焕发新的生机与活力是值得探索和实践的.
需要值得提出的是,无论哪种形式的教学改革,最终的目标都要落实到立德树人,培养学生学会主动思考,让每一位学生发自内心地学习,否则谈不上对学生思维能力的培养和创新能力的培养,更谈不上完成教学上的两性一度.问题情境设计对调动学生的积极性有着很好的促进作用,文献[4]探讨了高等数学课程教学中问题情境设计的一般途径和方法,但针对具体的教学内容,应该采用灵活的创新教学手段.微分几何是数学类本科生的一门综合性课程,课程难度很大,需要较强的空间想象能力和直觉能力.伪球面作为负常数高斯曲率曲面以及双曲几何的典型模型,是微分几何中的一类重要曲面,但由于其形状奇特,方程复杂,性质抽象不易理解.如果采用传统的讲授方式,学生会感觉索然无味,教学效果会大打折扣,更谈不上对学生思维能力和创新能力的培养.因此在授课内容无法更改和在大班授课的现实条件下,以案情推进式呈现教学内容,以探案式教学模式层层抓住学生的好奇心,以自制教具加强师生互动,以探究式启发式引导生生互动,以直观动画呈现加深学生理解,收到了良好的教学效果.
2 探案式教学的设计思路与实践
探案式教学设计思路如下:
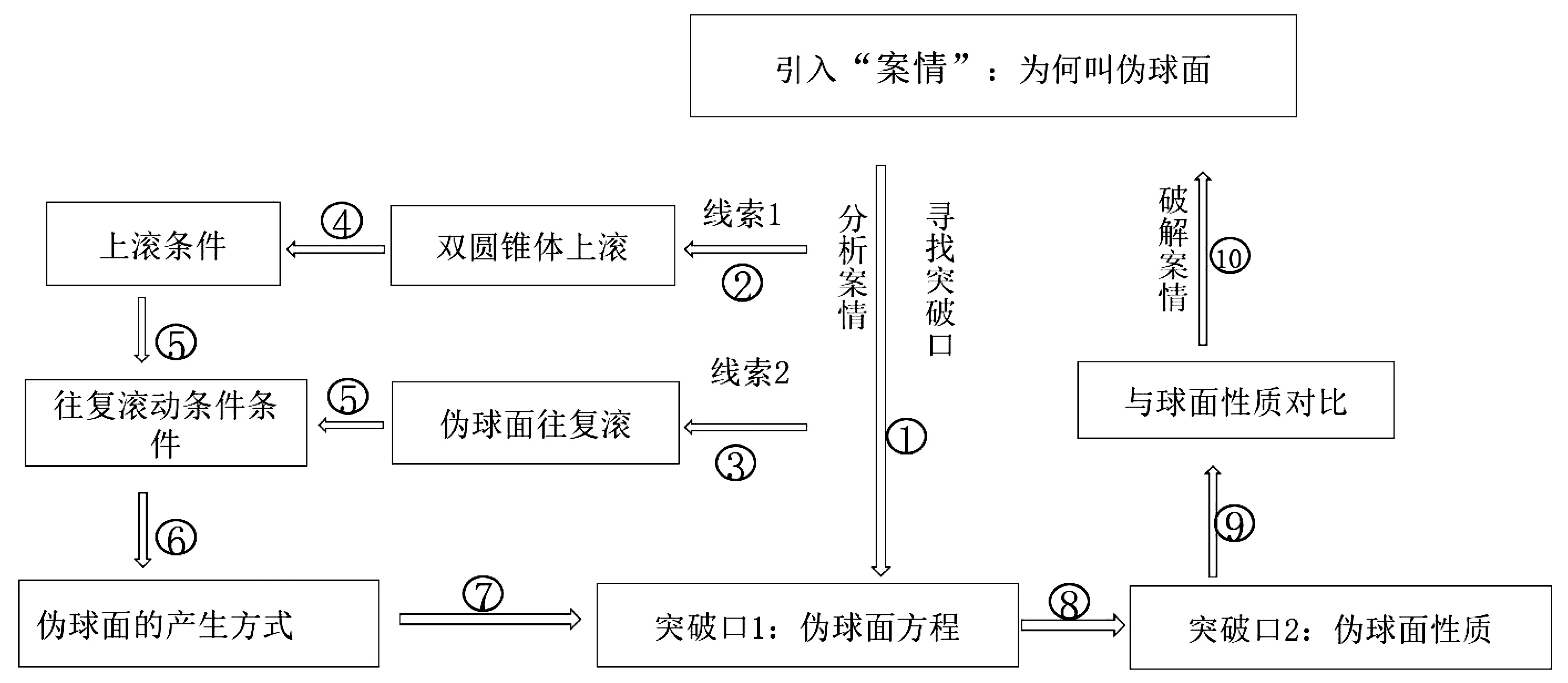
图1 探案式教学设计思路
2.1 以自制教具加强师生互动,引入“案情”
上课一开始,先让同学观察自制的实验装置图2的特点:两根直杆组成斜坡,左窄右宽、左低右高.另外还有三个物体,一个圆柱体,一个双圆锥体,一个形似双唢呐的物体,再让同学们猜想如果把这三个物体放在架子上会怎么滚动呢?大多数同学的直觉是三个物体由高处往低处滚动,此时让学生亲自上讲台操作实验,实验的结果只有圆柱体由高处向低处滚,双圆锥体却是从低向高处滚动,而形似双唢呐的物体放在装置上“上下”往复滚动.这样实验装置的引入,以及有悖于常识的实验结果,即使是大班授课,也可以将每个同学的注意力吸引过来,实验结果同直觉相悖更是引起了同学们强烈的好奇心.此时给学生公布“案情”,这个形似双唢呐的物体在装置上“上下”往复滚动的物体的外表面就是“伪球面”.显然其形状和球面相去甚远,那么为什么叫它伪球面,它和球面有什么关系?这个“伪”字又体现在哪呢?这样就给学生明确了本次课要破解的“案情”.

图2 自制教具
2.2 以探究式教学加强生生互动,寻找“案情”突破口
既然伪球面形状与球面完全不同,那么研究它和球面的关系,可以从建立它的曲面方程入手,但如何建立方程呢?通过它在装置上往复运动就能建立它的方程吗?很难找到切入点.那又应该从哪入手呢?此时让学生相互讨论,找到往复运动的原因,凭借物理学知识,同学们很快就能判断出是重心的高度变化引起的,但伪球面的重心为何会反复高低变化呢?既然双圆锥体相比伪球面简单的多,那么我们就应该从简单问题入手,分析双圆锥体向上滚动的时候重心下降的条件,看能否找到建立伪球面方程的突破口.
2.2.1 分析线索1:双圆锥体上滚
此处让学生展开讨论.显然,双圆锥体上滚过程中与轨道相接的部分圆半径变小,而轨道的倾斜又将双圆锥体向上做了部分抬移,如果这个抬移幅度不能够弥补半径差,双圆锥体重心下降从而出现上滚.显然这个抬移幅度与双圆锥体的形状,装置的斜面倾斜程度及轨道的夹角有关.令α为双圆锥体半顶角,β为轨道半夹角,θ为斜坡面中心线仰角.
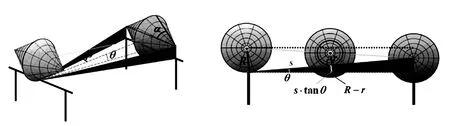
图3 侧视图
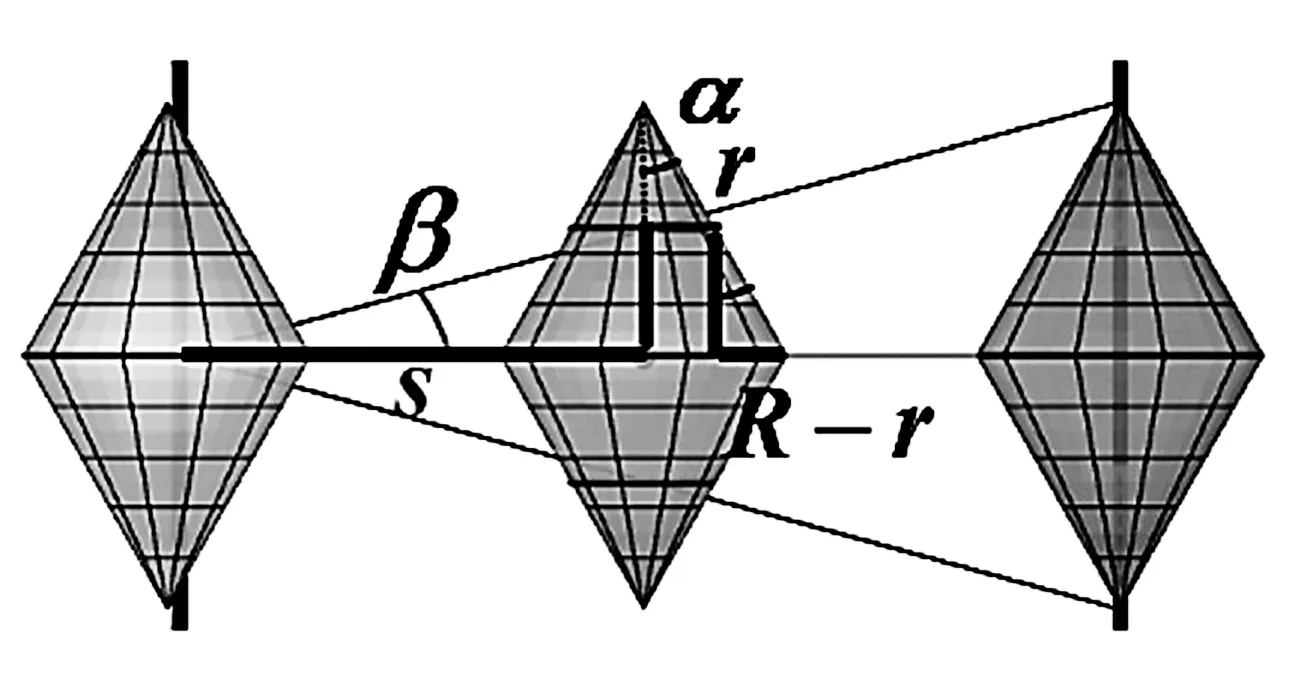
图4 俯视图(视线垂直于斜坡平面)
设双圆锥体底面圆半径为R,沿着斜坡面移动s时,由于轨道宽度变大,双圆锥体与轨道相接的部分圆半径变小,设为r,由侧视图可知,“上”滚时轨道对双圆锥体的抬移幅度为stanθ,如果这个抬移幅度不能够弥补半径差,即stanθ
分析出了双圆锥体上滚的不等式条件后,继续引导学生分析,双圆锥体有没有可能在轨道上静止不动?还是下滚呢?从而引导学生得到双圆锥体上滚、下滚及不滚的条件.总结如下:
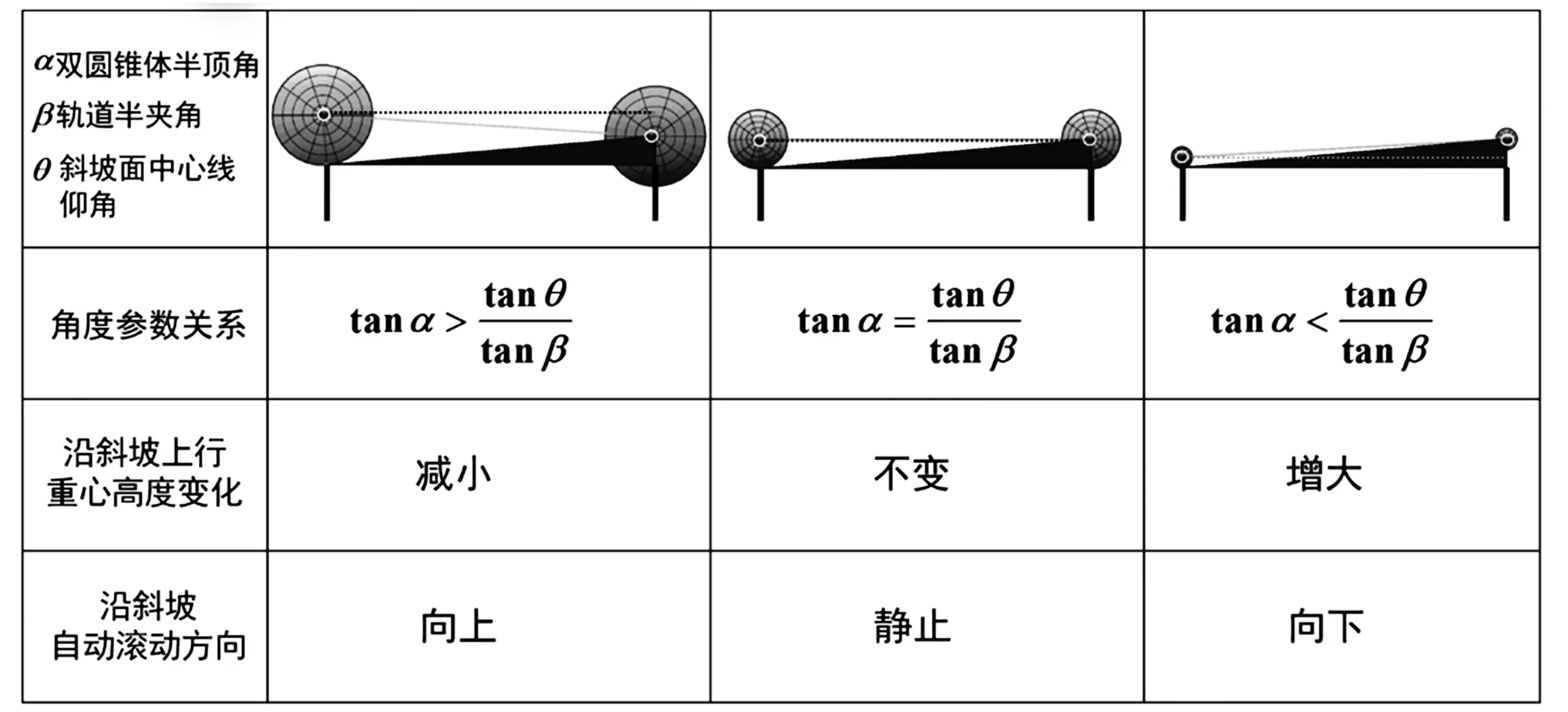
图5 双圆锥体滚动条件
2.2.2 分析线索2:伪球面上下往复滚动
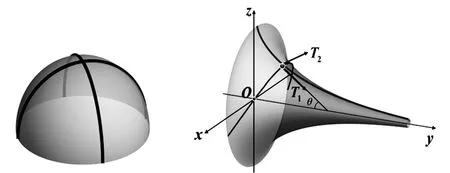
伪球面为什么能上下往复滚动?此处继续引导学生思考,能否利用双圆锥体的滚动条件分析出伪球面的特点呢?由于装置中轨道半夹角β和斜坡面中心线仰角θ这两个参数固定不变,注意到过伪球面与轨道接触点截伪球面所得的圆一定在某个双圆锥体上,那么伪球面在上下往复滚动中圆锥体的半顶角α会变化,若伪球面先由低向高处滚动,那就是开始重心是下降的,即tanα>tanθ/tanβ,既然中间会停下又出现向下滚动,应该在上滚过程中滚动过程中α逐渐变小,某一时刻等式会成立,即tanα=tanθ/tanβ,之后由于惯性作用会继续的向上滚动,此时满足不等式tanα 图6 伪球面上下滚动原理 分析了伪球面上下往复滚动的原理,接下来的关键问题是:能否借助双圆锥体构造出伪球面呢?注意到伪球面为一光滑的曲面,那么伪球面与轨道接触点的圆所在的圆锥体的半顶角在往复滚动中是连续变化的,此时让学生继续讨论思考,讨论发现,如果保持圆锥体斜高不变,将顶角连续变化的圆锥面堆叠形成的旋转曲面在滚动过程中就可以满足往复滚动的条件,至此,我们一起得出了伪球面的构造特点,如图7所示,“案情”获得重大进展,接下来只需要求出这个旋转曲面的方程即可.而求旋转曲面的方程,只需求出母线的方程,那么母线方程又应该怎么求呢?就需要继续分析伪球面构成的线索. 图7 (右半)伪球面生成图 由堆叠过程的特点,如图7建立坐标系,那么该旋转曲面可以由曲面在yOz面上的截线绕y轴旋转而成.而这个截线的特点是每点的切线被y轴所截的切线段恰好就是圆锥体的斜高,显然这些线段的长度相等.而满足这个特点的曲线恰好就是之前我们学过的直线的曳物线.而这个“上下”往复滚动物体的表面就是由曳物线绕y轴旋转而成的旋转曲面,曳物线就是这个旋转曲面的母线.曳物线(母线)的方程学生可以自行写出: 方程中a的意义为每点切线被y轴所截的切线段长.注意前面只是借用伪球面的称呼,现在就可以给出伪球面的严格定义. 定义将曳物线绕其渐近线旋转一周所得的旋转曲面称为伪球面. 此时,学生参与,写出伪球面的参数方程: 至此,“案情”的第一个突破口获得解决. 得出了伪球面的参数方程,但仅从方程上来看,还是没有揭示它为什么被称为“伪球面”以及它和球面的关系,这时候继续启发学生继续探析,应该从哪些角度进一步研究伪球面呢?由此引出研究伪球面的性质. 性质1伪球面的面积. 学生经过简单计算,可以得出右半伪球面面积 故伪球面的面积S=2S右=4πa2,恰好和半径为a的球面的面积相等. 性质2伪球面过y轴的截面面积. 球面过中心轴平面截得的大圆面积均为常数,那么伪球面过中心轴的截面面积是否和球面的截面有什么联系呢?由于y轴就是伪球面的中心轴,由伪球面的对称性,伪球面过y轴的截面面积就等于曳物线与y轴正向所夹区域的面积的四倍,所以只需要计算出曳物线与y轴正向所夹区域的面积.由曳物线的方程,利用反常积分学生可以得到y>0,z>0部分的截面积为 故伪球面过y轴的截面面积为S=4Sy>0,z>0=πa2,显然,该面积恰好是半径为a的圆的面积. 至此,探案过程过半,已经揭露了伪球面同球面具有某些相同的性质,叫它伪球面有一定的道理,但既然叫伪球面,就不是真正的球面,那么,“伪”又体现在什么地方呢?因为我们研究的对象为曲面,而高斯曲率是刻画曲面弯曲的重要特征之一,因此我们就需要研究伪球面的高斯曲率. 性质3伪球面的主曲率和高斯曲率. 图8 球面和伪球面的主方向对比 r=r(θ,φ)=(x(θ,φ),y(θ,φ),z(θ,φ))r(θ,φ) 通过计算伪球面的第一基本量E,F,G和第二基本量L,M,N, E=rθ·rθ=a2cot2θ,L=rθθ·n=±acotθ, F=rφ·rθ=0,M=rθφ·n=0, G=rφ·rφ=a2sin2θ,N=rφφ·n=±asinθcosθ, 总结上面的分析过程,伪球面的表面积,过中心轴的截面面积和球面完全一样,高斯曲率和球面只差一个负号.伪球面是一种具有负常数高斯曲率的曲面,弯曲程度与球面相同,弯曲方式不同,从这个意义上来讲,称之为伪球面不无道理,至此,“案情”真相大白.而我们层层推进的探案式的教学过程正是发现问题、解决问题的科研创新能力的培养过程,探案式的教学模式牢牢抓住了每个学生的好奇心,他们全程参与到“探案”过程,整个过程学生们都处于兴奋状态,很少有学生出现分神、瞌睡现象,收到了意外好的教学效果. 以微分几何伪球面一节的授课内容为例,以有悖直觉的滚动实验引入“案情”,以探案式的方式引导学生层层分析线索,借助图形、动画等多种教学形式和手段生动展开,在传统课堂中实现了师生互动和生生互动,学生充分参与到课堂中来,在学生的“探案”过程中培养自主创新的能力,达到了如期的教学效果.当然,由于伪球面知识点的特点,我们采用探案式可以更好地打造活力课堂,对于其它的内容,我们可以根据不同的授课内容,设计不同的教学方法和手段,以达到最好的教学效果. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.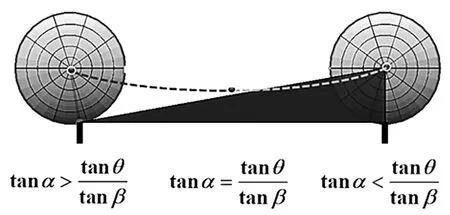

2.3 师生互动,乘胜追击,破解“案情”

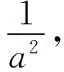
3 结 论

