基于改进鲸鱼算法虚拟电厂经济优化调度

程萱，付光杰，张晓莹，张梦迪

（东北石油大学电气信息工程学院，黑龙江大庆 163318）

目前，全世界经济快速增长，各个国家对于能源的需求越来越大，为了缓解能源短缺和解决环境恶化问题，风能、光能等新能源开始受到所有国家关注，但是这些能源在接入时有着显著的间歇波动性，使接入电力系统的功率输出充满不确定性，也不利于充分进行经济优化调度。此外，这些不确定的分布式电源(Distributed Generator,DG)在一定程度上会增加电力系统的成本。而选择虚拟电厂(Virtual Power Plant,VPP)正好解决了分布式电源接入电力系统所带来的不确定性问题，可以充分发挥分布式电源的经济性[1-5]。VPP 可以将不可控的能源、可控能源、储能进行结合，通过统一的控制实现功率需求参与电力系统运行，从而实现经济优化运行[6]。

国内外很多学者都看到了VPP 的优势，开始对VPP 的优化策略和运行模型展开了深入的研究。文献[7]提出了两阶段优化模型，这个模型不仅可以降低可再生能源输出波动性还可以提高系统运行经济性。文献[8]研究了基于风险惩罚机制的虚拟电厂的优化调度。文献[9]研究了基于使用时间价格的风、光、气、储虚拟电厂的经济调度，以实现经济优化。文献[10]研究了基于多虚拟电厂博弈的区域电网经济调度问题。文献[11]研究建立了虚拟电厂的两级博弈模型，并利用协同免疫量子粒子群算法实现了VPP 经济优化。以上VPP 调度都是仅从某个方面考虑VPP 优化调度建立相关模型，未充分分析优化调度的精度。

该文通过建立VPP 的经济模型，以获得最大收益为目标，优化调度VPP 中各能源单元的功率输出，以实现经济最大化，将鲸鱼算法运用到已建立好的VPP 经济优化调度模型中，并通过求解验证了模型的正确性和实用性。然后对鲸鱼算法的收敛因子进行了改进，并通过仿真比较了改进后的鲸鱼算法是否提高了收敛速度和精度。

1 VPP经济模型

1.1 目标函数

建立了含分布式不可控能源、可控能源和储能的VPP 的最大经济效益目标函数，建立了实时市场VPP 经济优化目标函数[9]：

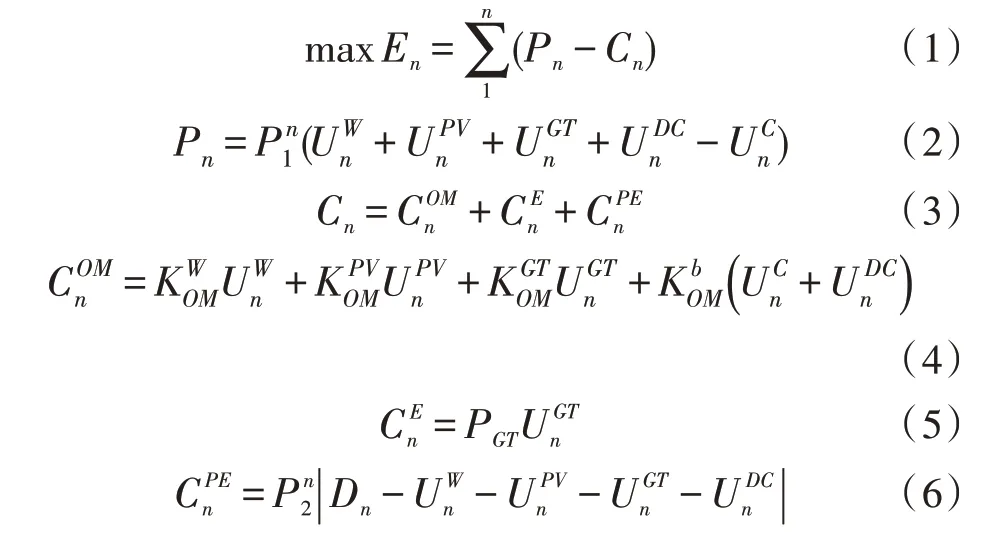
式（1）～式（6）中，n表示时间序列，以30 min 为一个时间间隔，n的取值为1～48 范围内的正整数；En表示n时段VPP 的净收益；Pn表示n时段VPP 的收益；Cn表示n时段VPP 的总成本；表示n时 段的售电电价；(充)、(放)表示风电、光伏、燃气轮机、储能装置在n个周期内的充放电功率；表示VPP 在n个周期内的运行成本、能耗成本和惩罚成本；表示风电、光伏、燃气轮机、储能装置在n个周期内的运行管理成本系数；PGT表示燃气轮机每单位发电量的燃料成本；表示n时段的购电电价；Dn表示n时段VPP 的申报计划。

1.2 约束条件

功率平衡约束：

式中，Δ 表示n时段的VPP 出力偏差。

储能电池电量约束：

式中，表示储能蓄电池在n时段内储存的电量；ηc、ηd表示蓄电池充放电的效率。

可控电源功率约束：

态下的功率上下限。

不可控DG 爬坡率约束：

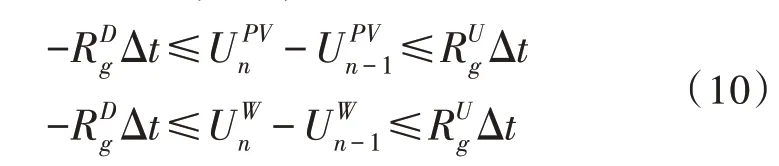
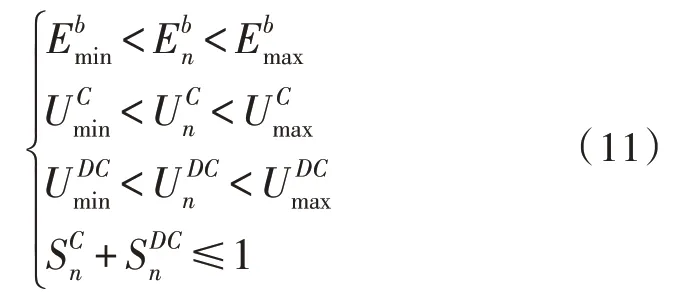
1.3 VPP运行控制策略

正常工作时，VPP 主要由风电、光伏等不可控的分布式电源提供电能[12-13]。当VPP 的风电、光伏发出的功率不足以满足负荷需求时，储能装置放电输出功率到电网。若此时还不满足，根据实时电价，考虑是接入可控电源成本低还是从电网中购买电量成本低；当购买成本高于发电成本，由可控电源发电提供能量，反之，从电网购买电量并让可控电源停机；若不可控的分布式电源提供电能可以满足负荷需求，此时储能装置充电，可控电源停机。

2 鲸鱼算法

2.1 基本鲸鱼优化算法

基本鲸鱼优化算法（Whale Optimization Algorithm，WOA)是一种新兴的仿生智能优化算法，它是从座头鲸独特的觅食行为中得到启发，并且对其进行模仿。WOA 算法可以主要分为3 个阶段：搜索觅食、收缩包围和螺旋更新位置。搜索觅食阶段指的是鲸鱼在一定区域内寻找食物的整个过程，算法中的鲸鱼是独立的个体，它可以根据其他鲸鱼的位置随机搜索，在这个阶段，数学模型可以表示为：

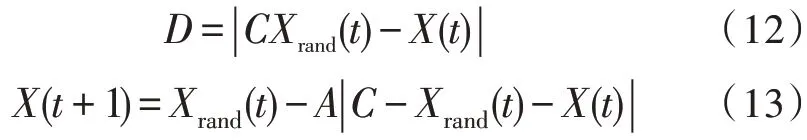
式（12）中，Xrand(t)是从当前鲸鱼种群中随机选择的鲸鱼个体，X(t)是当前鲸鱼的个体位置。式（13）中A和C是系数向量，其公式为：

式（14）和式（15）中，r1、r2的取值范围为[0，1]，a表示控制参数，随着迭代次数t的增加，其值从2 线性减小到0，即：

式中，max_iter为最大迭代次数。当 |A| ≥1 时，鲸鱼进入搜索和觅食阶段，个体鲸鱼会根据相位位置随机搜索。

鲸鱼个体的捕食行为过程包含收缩包围和螺旋更新位置这两个阶段。当 |A| <1 时，鲸鱼个体会向着当前位置最优的鲸鱼靠近。收缩包围阶段的数学模型可表示为：

式中，Xbest(t)是当前鲸鱼群体中位置最佳的个体，A|C-Xbest(t)-X(t)|为包围步长，此时|A|越大，鲸鱼游走的步长越大。

在螺旋更新位置阶段，鲸鱼在接近最佳鲸鱼个体的同时，也会以螺旋方式进行游走觅食，搜索鲸鱼个体至最佳个体之间可能存在的最优解。螺旋更新位置过程的初始点为当前鲸鱼个体的位置，它们的目标终点是当前最佳鲸鱼个体的位置。其数学模型可表示为：

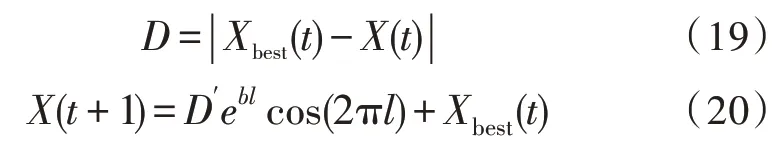
式（20）中，D′表示当前鲸鱼个体与处于最佳位置的鲸鱼之间的距离，b是常量系数，l是[－1，1]之间的随机数。

搜索觅食、收缩包围和螺旋更新位置3 个阶段的选择是由概率因子p和系数|A|的值共同决定的。当p≥0.5 时，进入螺旋更新位置阶段；当p<0.5，进入搜索觅食阶段和收缩包围阶段，数学模型如下：

2.2 改进鲸鱼算法

与其他智能算法类似，鲸鱼算法也存在处理优化过程时全局搜索和局部搜索不能平衡的问题[14-16]。当|A|≥1 时，算法的主要目的是进行全局最优；当 |A|<1时，算法的主要目的是进入局部最优搜索。其中，控制参数线性变化时不能很好地调节鲸鱼算法的搜索能力，因此提出一种非线性的计算方法，即：

算法在后期搜索时，会产生一些问题，即容易陷入局部最优和出现早熟收敛的现象。为了解决该问题，并且对性能进行改善，该文采用的策略为自适应权重，公式可表示为：

则式（21）可变为：

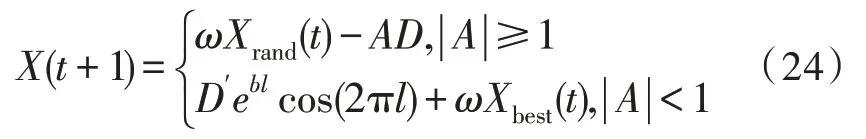
算法的优化流程图如图1 所示。

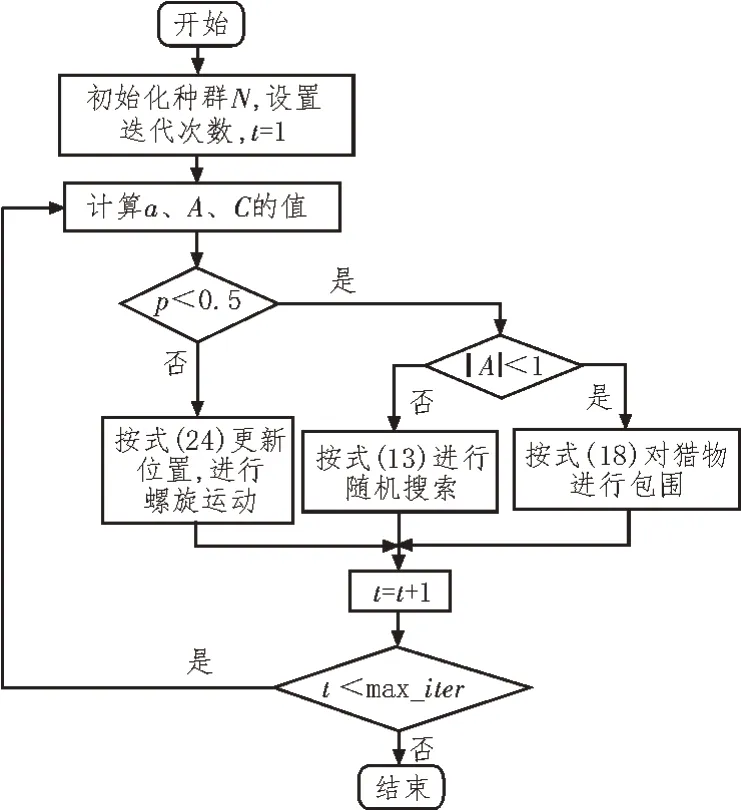
图1 改进鲸鱼算法实现流程图

3 算例分析

3.1 数据采集

VPP 中包括3 个不可控DG，分别是两个500 kW的风力发电和一个100 kW 的光伏发电，其运行参数如表1 所示。VPP 中可控能源的输出功率假设为500 kW，储能装置的容量假设为500 kW。该文燃气轮机出力系数取为1，随机选取我国某地区在某天的数据表进行分析。图2 为某天以30 min 为间隔的预测负荷。

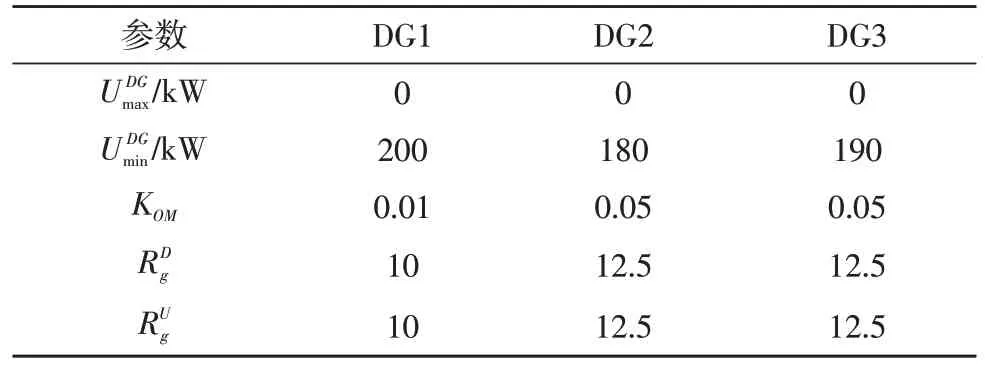
表1 DG运行参数

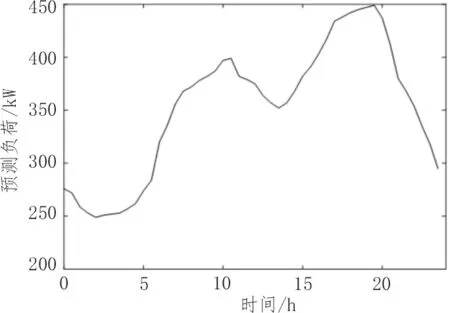
图2 某天预测负荷数据曲线

此外，预测VPP 次日出力还需考虑分时电价。在图3 中，虚线表示实际市场电价价格数据，实线表示日前市场电价价格数据。

图3 某天电价数据曲线

3.2 结果分析

在VPP 优化过程中，储能装置依据负荷的需求及考虑VPP 运行经济成本控制充放电状态。优化调度结果如图4 和图5 所示。

图4 VPP电源输出功率曲线图

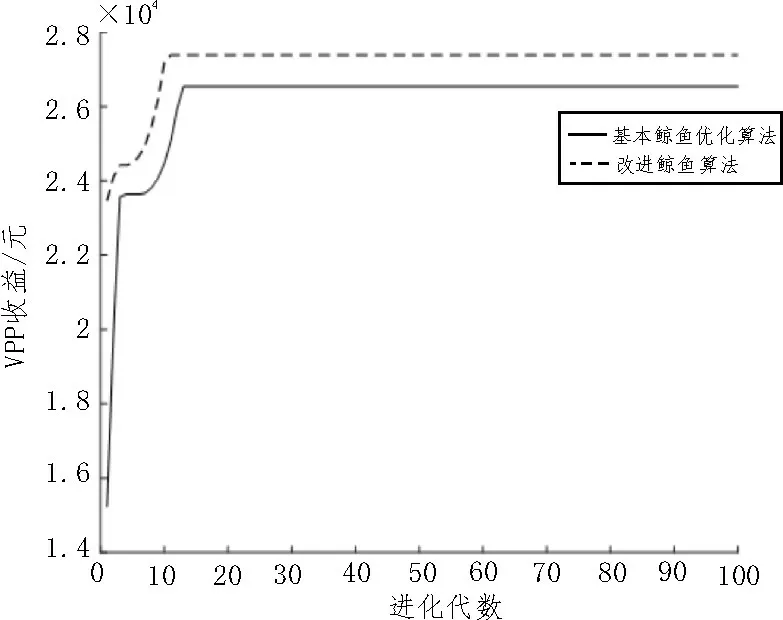
图5 VPP最大经济收益迭代图

图4 所示为VPP 中各电源输出功率的曲线图，在VPP 优化过程中，从储能装置的充放电功率曲线可以看出，当其值大于0 时，表示储能装置此时正处于充电状态；当其值小于0 时，表示储能装置此时正处于放电状态；当其值等于0 时，表示储能装置此时正处于不工作状态。

从图4 中可以看出储能装置在一整天的工作状态，当不可控电源供电不足以满足负荷需求时储能装置就需要放电。由图4 可以看出，10∶00～15∶00，17∶00～21∶00 时储能装置处于放电状态，当不可控电源的供电刚好足以满足负荷的需求，并且有富余，这时可以对储能装置进行充电，0∶00～10∶00，15∶00～17∶00，21∶00～24∶00 储能电池充电。图中的曲线斜率的陡缓，可以反映出储能装置在进行充放电时的速度快慢。

由上述分析可知，储能装置在VPP 运行过程中处于充放电状态，这主要是由于不可控的DG 输出的功率不确定引起的，其中储能装置的作用是稳定功率输出[17]。

图5 为采用鲸鱼算法和改进鲸鱼算法求解VPP在该算例的最大经济收益优化的结果迭代对比图，图中实线为改进后的鲸鱼算法优化迭代过程，由图5可知改进后的鲸鱼算法在VPP 优化调度过程中迭代次数在10 次时已经收敛，而基本鲸鱼算法在VPP 优化调度过程中迭代次数在15 次时已经收敛，采用改进鲸鱼算法收敛速度得到一定的改善。此外，改进鲸鱼算法的收益优化结果为2.738 万元，基本鲸鱼算法的收益优化结果为2.654 万元，收敛精度得到进一步提高。

4 结论

该文基于VPP 的架构，研究了VPP 的基于分时电价的经济优化调度模型。依据负荷需求，合理调度VPP 中各能源系统，考虑分时电价优化VPP 中可控能源的工作状态，目标是获得虚拟电厂最大经济效益，将鲸鱼算法运用到已建立好的VPP 经济优化调度模型中，并且对其进行求解。算例结果表明，建立的优化调度模型的可行性和鲸鱼算法可以很好地完成VPP 的优化调度，使VPP 能较好地参与电能交易。同时，采用鲸鱼算法和改进鲸鱼算法求解VPP在该算例的最大经济收益，通过比较可以看出，改进算法的收敛速度和收敛精度都有所提高。