桂东南容县非饱和花岗岩风化土的土水特征

赵瑞华，韦文智，廖丽萍†，文海涛，杨云川，许英姿

(1.广西大学土木建筑工程学院，530004，南宁；2.工程防灾与结构安全教育部重点实验室，530004，南宁；3.广西防灾减灾与工程安全重点实验室，530004，南宁；4.广西壮族自治区地质环境监测站，530028，南宁)

桂东南容县花岗岩风化土在天然状态下呈硬塑态、抗剪强度高，但遇水易崩解软化，因此，在亚热带季风气候与充沛的降雨激发作用下，花岗岩风化土易失稳诱发崩岗、滑坡等地质灾害[1-2]，不仅造成严重的水土流失，而且掩埋农田、房屋和公路，严重威胁到人民的生命财产安全，制约当地社会经济的发展。崩岗侵蚀、滑坡形成均与降雨入渗过程及其土体自身的渗透性质相关[3]，因此，探明该区域花岗岩风化土的土水特征与非饱和状态时的渗透性是准确理解崩岗侵蚀过程与机理、滑坡形成的重要基础[4]。

土水特征曲线一般用含水率(或饱和度)与基质吸力的关系曲线来定量描述。目前，滤纸法、渗析法、压力板仪法等常用的试验方法虽然能获得一定范围的数据，但是难以描述整个基质吸力范围内的土水特征。因此，国内外学者采用Van Genuchten模型[5](简称VG模型)、Gardner模型[6]和Brook &Corey模型[7](简称BC模型)及各种修正模型等来克服上述缺陷。然而，实际应用中并没有严格划分上述模型的使用范围[8]。

非饱和土渗透系数与饱和土显著不同的是：它与含水率及基质吸力等密切相关，随时间变化。这是因为非饱和土孔隙中气体的存在，使得气液界面形成一层收缩膜，其不仅能堵塞水流动的通道，而且能影响水在土体骨架中的分布。如果工程设计将非饱和土渗透系数当作常量来考虑，计算结果势必会出现较大的误差[9]。可见，准确认识非饱和渗透系数具有重要的工程意义[10]。然而，因基质吸力的存在，稳态法、瞬时截面法及湿润锋前进法等直接测定非饱和渗透系数的方法存在成本高、耗时费力及测量精度不准确等缺点。为了避免上述缺点，国内外学者采用经验模型、宏观模型、统计模型等间接方法获得非饱和渗透系数。此外，在缺乏饱和渗透系数的条件下，叶为民等[10]还针对工程的不同需求，建立了土水特征曲线与相对渗透系数的关系。

花岗岩风化土这类特殊土具有强区域异质性，其土水特征及其非饱和渗透系数是否有别于其他区域的风化土？其特性如何？有待深入探讨。因此，笔者以桂东南容县花岗岩风化土为研究对象，采用压力膜仪法开展脱湿试验，研究各初始干密度条件下花岗岩风化土的土水特征，分析VG、Gardner和BC模型的适用性，预测非饱和风化土的相对渗透系数及探讨渗透系数的差异，旨为崩岗侵蚀过程与机理、滑坡形成研究提供科学支撑。

1 研究区概况

桂东南容县(E 110°15′00″～110°53′00″，N 22°27′00″～23°07′00″)地处北回归线以南，面积2 257.39 km2。岩土体类型为岩浆岩、碎屑岩、变质岩和第四系松散土体，其中，岩浆岩的分布面积最大，占55.83%，岩性为花岗岩。花岗岩风化层最厚可达30 m。因为花岗岩风化土的表层依次为残积土、全风化土，且该层也是崩岗(图1a)发育与滑坡(图1b)滑动面的主要区域[2]，因此，笔者以花岗岩残积土和全风化土为重点研究对象。

图1 容县六王镇野外调研照片Fig.1 Field survey photos of Liuwang town in Rong county

2 试验设计与方法

试验土体为容县滑坡高易发区-六王镇[2]典型滑坡的花岗岩残积土和全风化土，取样剖面自上而下依次为残积土层(揭露厚度为11～20 m，图1c)、全风化土层(揭露厚度为10～15 m，图1d)、强风化层(揭露厚度为1～2 m)及中～弱风化层。根据GB/T 50123—2019《土工试验方法标准》的试验步骤[11]，获得花岗岩残积土和全风化土的最大干密度和最佳含水率分别为1.73 g/cm3和17.20%、1.83 g/cm3和13.77%；2者的物理性质指标和颗粒级配累计曲线如表1和图2所示。由表1可知，残积土与全风化土的液限均<50%，塑限指数分别为14.8和8.7。由图2可知，残积土主要由砂粒(粒径0.075～≤2.000 mm)和细粒(粒径≤0.075 mm)组成，其中，粗砂(0.500～≤2.000 mm)质量分数最高，为36.96%；其次是细粒，为23.54%，而中砂(0.250～≤0.500 mm)和细砂(0.075～≤0.250 mm)质量分数相对较少，分别为10.97%和17.88%。全风化土主要由砂粒组成，其中，粗砂质量分数最高，为36.64%；其次是细砂，为26.33%，而中砂和细粒质量分数仅为11.02%和9.23%。这表明残积土粒度呈现中间小、两边大的特征[12]；全风化土粒度具有“大小”交替变化的特征。根据JTG 3430—2020《公路土工试验规程》[13]划分标准：2种土均属于砂类土；根据细粒含量、细粒土与A线间的位置[13]，残积土为粉土质砂，全风化土为含细粒土砂；不均匀系数Cu和曲率半径Cc分别为26.61、10.40，1.03、0.55；残积土级配良好，而全风化土级配不良。基于上述数据及花岗岩风化土滑坡勘察中土工原位试验数据，本试验土样的初始干密度被设置为1.3、1.4、1.6和1.7 g/cm3；试验均设置2个平行试样，其结果由平均值确定。

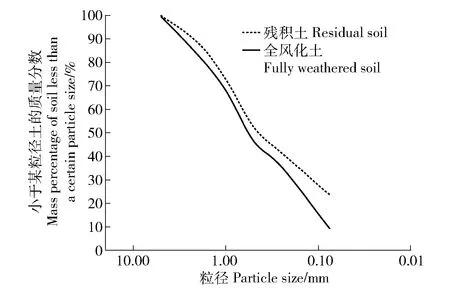
图2 土的粒径级配累计曲线Fig.2 Cumulative curve of grain size grading of soil

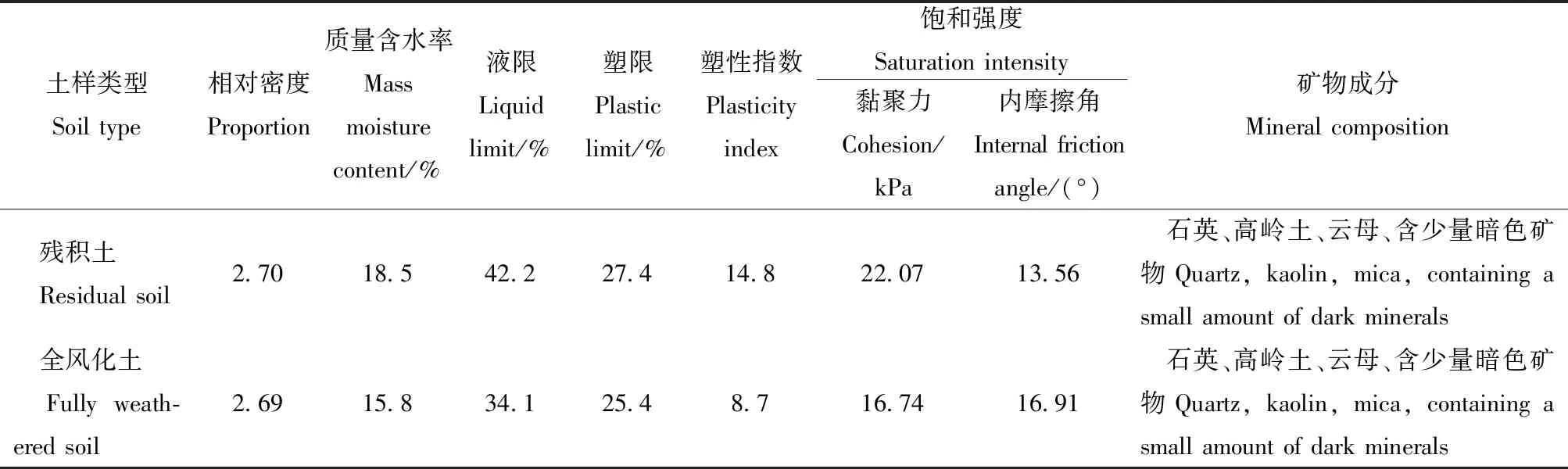
表1 花岗岩残积土、全风化土的物理性质指标Tab.1 Physical properties of granite residual and fully weathered soil

美国麦克AutoPore IV 9500型压汞仪开展压汞试验，得到各初始干密度的残积土与全风化土的孔径分布曲线。因论文篇幅限制，仅展示初始干密度为1.4 g/cm3的残积土与全风化土的孔径分布曲线(图3)。由图可知，全风化土的孔径分布较残积土均匀，且孔径分界点较小；2种土的孔径范围为1～106nm，曲线呈现“双峰”特征。根据Kodikara等人对孔隙的划分标准[14]可知，残积土与全风化土的孔隙主要为颗粒间孔隙(4～103nm)与集聚体间孔隙(104～106nm)。

利用美国1500型15 bar压力膜仪开展土水特征曲线试验(图4，时间：2020年7—11月)，采用击实法制备重塑土样。首先根据初始干密度及质量含水率(均设置为14%)配置土料，然后倒入制样桶中，经均匀锤击后取出土饼，用已涂抹凡士林的切土刀将土饼削成略大于环刀直径的土柱，随后将环刀垂直向下压，边压边削至土样高出环刀，再削平环刀2端土样及擦净环刀外壁，称量环刀和土的总质量并测含水率。不断重复上述操作，直至干密度差值为±0.1 g/cm3和含水率差值为±2%，试样制备完成；紧接着用真空缸对制备好的试样进行抽气并注水饱和，最后放置于陶土板上，逐级加载。每级压力为：1 kPa→10 kPa→50 kPa→100 kPa→250 kPa→500 kPa→750 kPa→1 000 kPa。每级压力加载完毕后保持不变，直至排出的水质量不变，试样被取出称量为mi。当试验结束时，试样被烘干，获得干土质量为ms。体积含水率可通过下式计算：

图4 压力膜仪Fig.4 Pressure film instrument

θ=(mi-ms-m环)/ρwV。

(1)

式中：θ为体积含水率，%；m环为环刀质量，g；ρw为水的密度，ρw=1 g/cm3；V为环刀总体积，cm3。

3 结果与分析

3.1 试验结果分析

由于初始干密度为1.3 g/cm3的残积土在抽气饱和后较难成样，故此研究不讨论该密度。其他试样的试验结果如图5所示。由图5a可知：初始干密度对残积土的土水特征曲线影响显著。当基质吸力<30 kPa时，干密度大的曲线位于干密度小的下方。然而，干密度大的土样中含有较为细致的孔隙，毛细作用影响较大[15]，导致其失水速率较干密度小的小，因此，随着基质吸力的增大，干密度大的土水特征曲线位于干密度小的曲线上方。这一现象在武汉非饱和粉质黏土、宜巴红层软岩泥化夹层中也出现[16-17]。此外，3种干密度的曲线均包含2阶段：第1阶段(1～10 kPa)和第2阶段(10～1 000 kPa)。第1阶段为边界效应段[18]，体积含水率变化较小。第2阶段为过渡段，由2个下降段及1个水平段组成；其中，第1下降段(10～50 kPa)较陡，体积含水率的减小幅度较大，这是因为气体处于孔隙连通或半连通状态。此外，干密度小的土样排水速度快、曲线斜率大。然而，当基质吸力约为30 kPa时，3种初始干密度的曲线出现交汇点。这是因为虽然干密度存在差异，但是土样仍具有相同数量的微小孔隙，所以当大、中孔隙的水分完全消散后，它们仍能具有相似的土水特征[19]。这一特征在玄武岩残积土中也存在[20]。此时，土体内部的优势孔隙主要为集聚体间孔隙。当基质吸力为50～250 kPa时，曲线处于水平段，孔隙处于气体连通的状态[21]。当孔隙到达孔径分界点[18](图5a，基质吸力为100 kPa)后，其优势孔隙转变为颗粒间孔隙，体积含水率再次随基质吸力的增大而减小，曲线进入第2下降段(250～1 000 kPa)。这种现象在初始干密度1.7 g/cm3的土水特征曲线中尤为明显。已有文献将分界点前的曲线称为低吸力段；该点后的曲线称为高吸力段[18]，因此，残积土的低吸力段与高吸力段分别为1～100 kPa和100～1 000 kPa。

由图5b可知，4种干密度全风化土的土水特征曲线均可划分为4个阶段。第1阶段(1～10 kPa)：体积含水率的变化较小。第2阶段(10～500 kPa)：虽然孔隙中存在分散的气泡，但是水气尚未分离，因此，排水通道顺畅，土样脱湿速度快。然而，当基质吸力为50～100 kPa时，体积含水率减幅相对较小，这是因为孔隙水与孔隙气体相互分离，排水通道受气体扰动而受到阻碍。第3阶段(500～750 kPa)：体积含水率的减小幅度较小，这说明全风化土中的孔隙已到达分界点(图5b，基质吸力为637 kPa)，此时虽然土体存在2种密度较高的孔隙，即集聚体间孔隙和颗粒间孔隙，但是起控制作用的孔隙已由集聚体间孔隙转变为颗粒间孔隙。第4阶段(750～1 000 kPa)：体积含水率减小幅度再次增大，且初始干密度为1.3和1.7 g/cm3的体积含水率的减小幅度较1.4和1.6 g/cm3的显著，但孔隙均主要为颗粒间孔隙。可见，4种干密度的第1、2、3阶段分界点前的曲线分别为低吸力段的边界效应段、过渡区的下降段及水平段，第3阶段分界点后的曲线和第4阶段分别为高吸力段中过渡区的水平段和下降段。此外，干密度为1.7 g/cm3的曲线基本位于其他3个干密度的最下方。

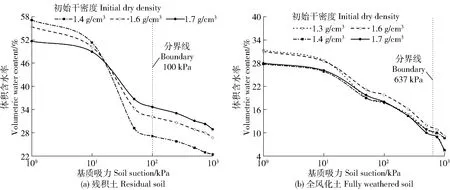
图5 风化土土水特征曲线Fig.5 Soil-water characteristic curve of weathered soil

以上结果表明：残积土与全风化土的土水特征曲线既存在共性，又具有差异性。共性表现在：1)曲线包含边界效应段和过渡段，均未出现残余段，呈现类似于红黏土的“双台阶”特征[22]。当基质吸力为750～1 000 kPa时，体积含水率均处于再次减小阶段，属于高吸力段中过渡区的下降段。2)孔隙均到达孔径分界点[18]，优势孔隙主要为集聚体间孔隙、颗粒间孔隙。差异性表现在：1)在相同的干密度及基质吸力条件下，残积土的体积含水率均较全风化土的大。2)当基质吸力为1～50 kPa时，残积土的脱水速率较全风化土的快。然而，当基质吸力为50～250 kPa时，却呈现相反的规律。3)残积土的曲线在基质吸力约为30 kPa处出现交汇点，因此，曲线与初始干密度的关系呈现2种相反的规律。然而，全风化土的土水特征曲线却未出现交汇点，程的影响较全风化土的显著。4)当初始干密度为1.4 g/cm3时，残积土与全风化土孔径分界点对应的基质吸力分别为100和637 kPa。

3.2 拟合结果分析

VG模型[5]、Gardner模型[6]和BC模型[7]等3个常用的4参数模型如式(2)至式(5)所示，其拟合参数如表2和表3所示。

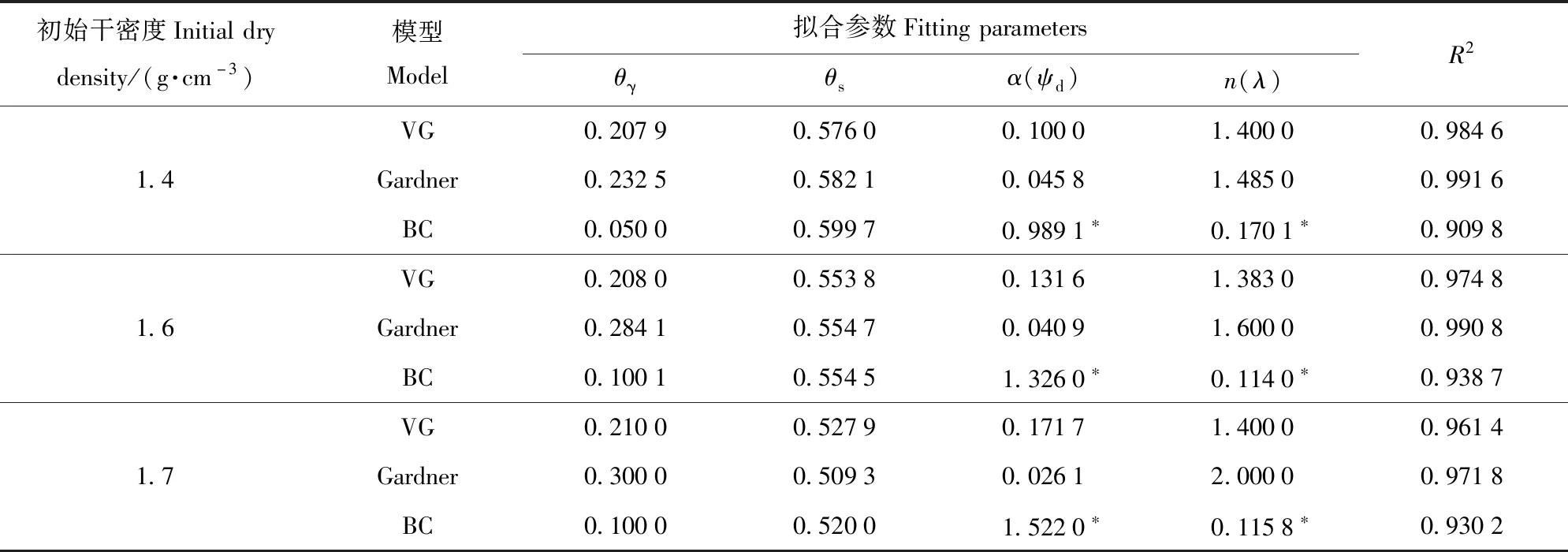
表2 残积土土水特征曲线的拟合参数Tab.2 Fitting parameters of soil-water characteristic curve of residual soil

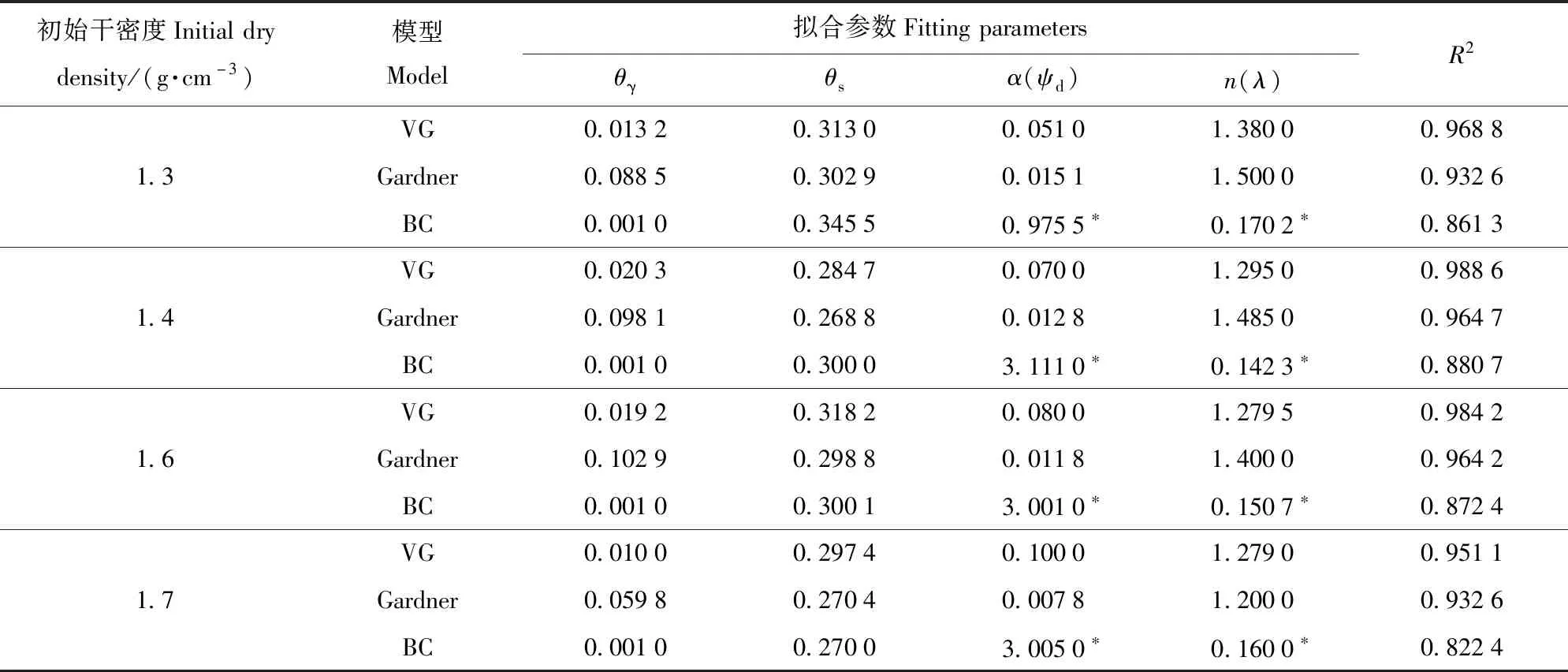
表3 全风化土土水特征曲线的拟合参数Tab.3 Fitting parameters of soil-water characteristic curve of fully weathered soil

VG模型拟合方程：

(2)

式中：θγ为残余含水率，%；θs为饱和含水率，%；α为进气潜能因子；ψ为土体基质吸力，kPa；n为孔径指数；m为曲线密和因子，m=1-1/n。

BC模型拟合方程：

(3)

θ=θs(ψ<ψd)。

(4)

式中：ψd为土壤进气值；λ为孔径分布指数，其他参数含义与VG模型相同。

Gardner模型拟合方程：

(5)

式中参数含义与VG模型相同。

由表2及表3可知：

1)虽然残积土和全风化土孔径指数n与孔径分布指数λ因干密度而变化，但是变化范围均较小。

2)同一干密度的全风化土n较残积土的小，而λ较大。因为λ和n的关系是λ=2/n+3[23]，所以，λ越大，孔径分布就越均匀。可见，全风化土的孔径分布较残积土均匀。该结果也与风化土孔径分布曲线结果相一致。

3)VG及Gardner模型对残积土的拟合相关系数R2均大于0.94，适用性好；而BC模型的适用性次之。对于全风化土，VG及Gardner模型的R2均>0.93，而BC模型对1.7 g/cm3的R2仅为0.82，可见，VG与Gardner模型对全风化土均有较好的适用性，而BC模型次之。原因有2方面：一是拟合参数的多解性；二是BC模型是一个分段函数，基质吸力大于进气值会导致拟合相关系数较低。

4 非饱和花岗岩风化土的相对渗透系数

根据3.2节的结果，选用VG模型[5]与Gardner模型[6]预测风化土的相对渗透系数，结合表2和表3的拟合参数，绘制出相对渗透系数与基质吸力的关系曲线(图6和图7)。

VG模型水力传导表达式[5]：

(6)

Gardner模型水力传导表达式[6]：

(7)

式中:Kr(ψ)为基质吸力为ψ时的渗透系数与饱和渗透系数比值，其余参数含义同3.2节。

4.1 残积土的相对渗透系数

由图6可见，VG与Gardner模型预测的相对渗透系数具有相似的变化特征：1)相对渗透系数均随基质吸力的增大而减小；2)在相同的基质吸力条件下，干密度大的相对渗透系数较干密度小的小。然而，2个模型的预测结果存在较大差异，对于干密度为1.4、1.6和1.7 g/cm3的残积土，VG模型预测的相对渗透系数分别为：8.145×10-8～0.366、4.134×10-8～0.297、1.611×10-8～0.264，而Gardner模型预测的相对渗透系数分别为：7.648×10-4～0.956、3.874×10-4～0.961、3.837×10-5～0.975。特别是当基质吸力为1～10 kPa时，2种模型预测的相对渗透系数最大差距达上100倍，且VG模型预测的相对渗透系数的减小幅度较Gardner模型的大。

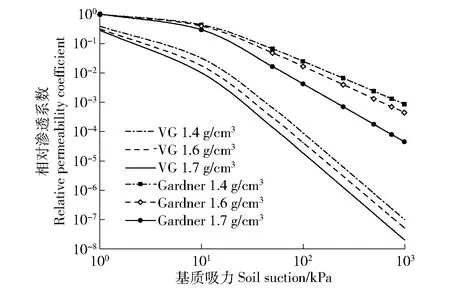
图6 残积土的相对渗透系数Fig.6 Relative permeability coefficient of residual soil

4.2 全风化土的相对渗透系数

由图7可见：1)相对渗透系数均随着吸力的增大而减小；2)对于干密度为1.3、1.4、1.6和1.7 g/cm3的全风化土，VG模型预测的相对渗透系数分别为：6.919×10-7～0.460、4.590×10-7～0.298、3.472×10-7～0.260、1.909×10-7～0.229，Gardner模型预测的相对渗透系数分别为：2.090×10-3～0.985、2.733×10-3～0.987、5.300×10-3～0.988、3.130×10-2～0.992。可见，干密度越大，VG模型的相对渗透系数越小，而Gardner模型的相对渗透系数却越大；3)VG模型的相对渗透系数预测值与Gardner模型的最大差距达数10万倍；4)VG模型预测值的总体减小幅度较Gardner模型的大。

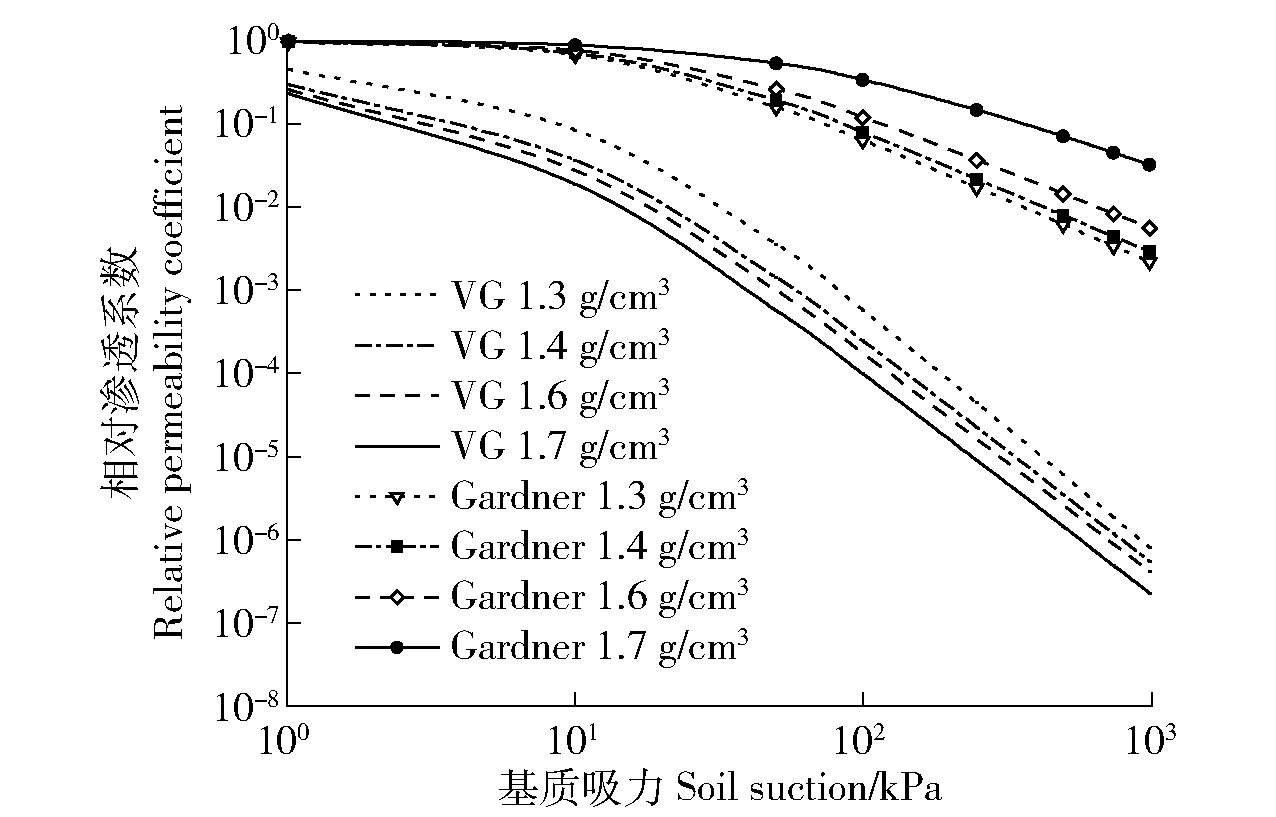
图7 全风化土的相对渗透系数Fig.7 Relative permeability coefficient of fully weathered soil

4.3 讨论

由4.1和4.2节可知，2种土的相对渗透系数均随基质吸力的增大而减小，且Gardner模型的预测曲线较VG模型的平缓。然而，它们却存在显著差异，主要为：1)残积土的VG预测值较全风化土的小，最大差距约10倍，而Gardner预测值的最大差距达上千倍。笔者将VG预测的相对渗透系数与试验的饱和渗透系数(残积土1.4、1.6和1.7 g/cm3分别为5.959×10-5、2.653×10-5和1.452×10-5cm/s；全风化土1.3、1.4、1.6和1.7 g/cm3分别为2.641×10-4、1.461×10-4、1.081×10-4和3.451×10-5cm/s)相乘，得到非饱和风化土的渗透系数(图8和图9)。由图8可知，2种土的渗透系数均随干密度的增大而减小；在相同的条件下，全风化土的渗透系数较残积土的大，且最大差距为30倍。这间接地反映容县花岗岩风化土边坡呈现上弱下强的不均匀空间渗透特性。这类特性与其粒度分布，特别是细粒含量有关[24]。换言之，虽然2种土均由砂粒和细粒组成，但是残积土中细粒含量较全风化土的多14.31%，因此，残积土的渗透能力较全风化土的弱。这类渗透差异会影响雨水转换为土壤水的速率与分布特征，致使斜坡土体抗剪强度空间异质性的发育，不仅在一定程度上决定着斜坡变形破坏模式[25]，而且对土壤侵蚀也有不容忽视的影响[24]。事实上，研究区滑坡的形成模式主要有渐进滑动型与突然整体溃滑型，这与入渗差异引起强度不同程度的丧失有关[26]。此外，崩岗侵蚀形式多样且类型复杂[1]，其中，条型和弧型的数量最多，且部分条形崩岗与滑坡还有着密切的联系，因为它们在滑坡形成后发生，并以滑体作为崩积体；滑体作为主要物源，其表层残积土因被扰动而结构性变差，抗冲蚀能力被削弱，细颗粒被雨水裹挟带走；随后侵蚀沟槽形成并扩大，滑体表层出现明显的水流粗化现象；雨水易穿透至全风化土层内，致使其强度丧失，龛形成并扩大，造成上部含水率大的土体因内力不平衡而塌陷，最终溯源侵蚀不断发生[27]，致使严重的水土流失，影响边坡的长期稳定性。2)残积土相对渗透系数的减小幅度均大于全风化土，且2模型的相对渗透系数均随着干密度的增大而减小；然而，Gardner预测的全风化土相对渗透系数却随着干密度的增大而增大。上述现象的主要因素为：土体类型、预测模型、拟合参数α和n对曲线位置和形态的综合影响[23]、基质吸力和干密度。例如，当α相同时，n越大，土水特征曲线的斜率越小；当n相同时，α越大，相对渗透系数曲线越陡。由表2及表3可见，在Gardner模型中，当残积土的干密度由1.4增至1.7 g/cm3时，α之间仅相差0.005～0.020，而n却增大0.4左右，此时图6中干密度1.7 g/cm3的残积土相对渗透系数曲线斜率较其他2个密度的小，且更靠近坐标系的左下方；当全风化土的干密度由1.3增至1.7 g/cm3时，α之间仅相差0.001～0.007，而n却减小0.2左右，此时图7中全风化土的相对渗透系数呈现与残积土不一致的规律。

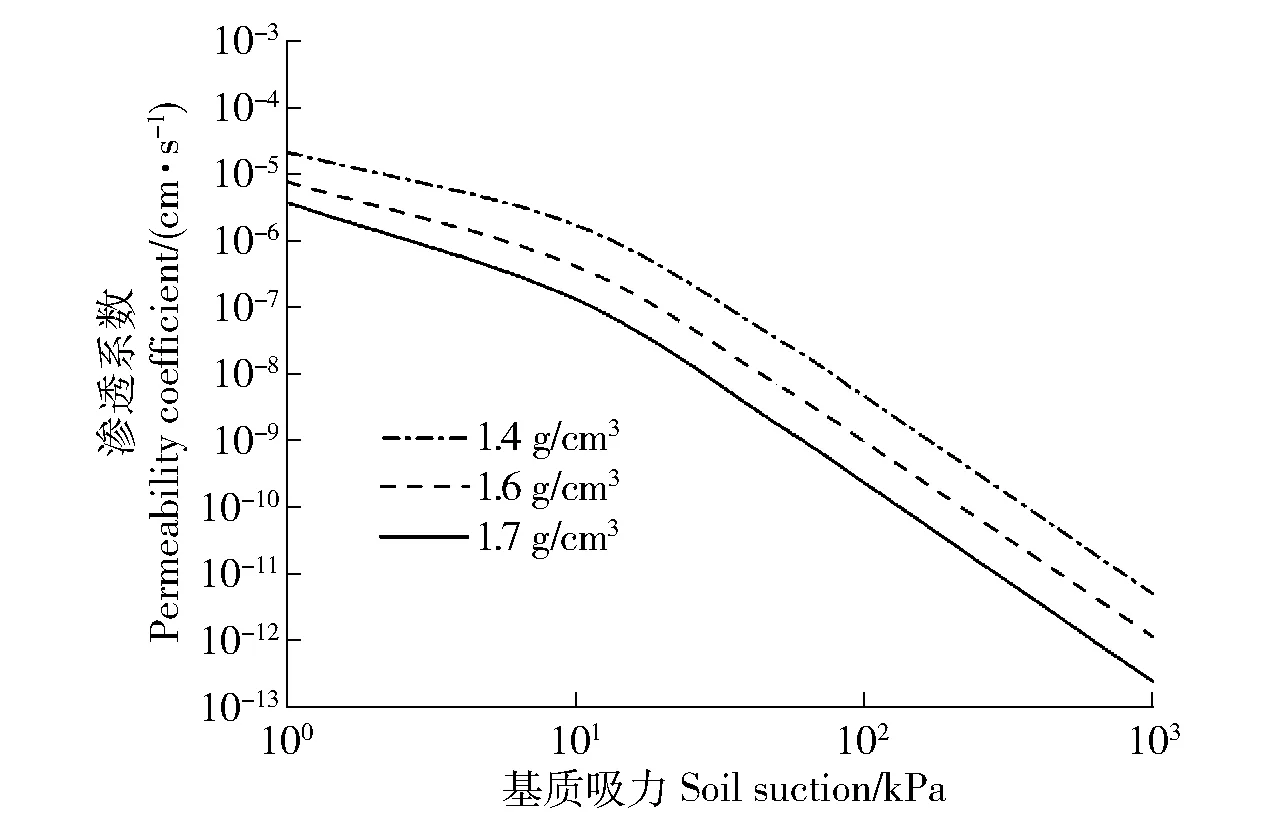
图8 残积土的渗透系数Fig.8 Permeability coefficient of residual soil

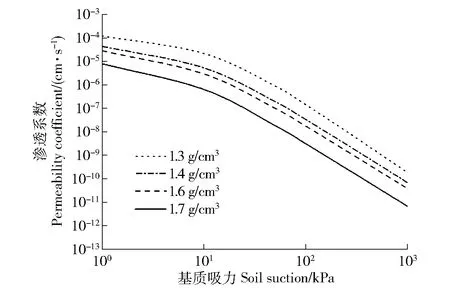
图9 全风化土的渗透系数Fig.9 Permeability coefficient of fully weathered soil

5 结论

1)残积土与全风化土土水特征曲线过渡段包含2个下降段及1个水平段，具有“双台阶”特征，其孔隙主要为集聚体间孔隙、颗粒间孔隙。然而，残积土的孔径分界点却较全风化土的大，其脱湿过程受初始干密度的影响也较全风化土的显著。

2)残积土与全风化土的孔径指数n与分布指数λ变化范围均较小。然而，同一干密度条件下，全风化土仍具有较低的n和较高的λ，孔径分布较残积土的均匀。

3)VG与Gardner模型对残积土与全风化土土水特征曲线拟合的相关系数R2均>0.93，适用性最好；而BC模型的R2最低仅有0.82，适用性次之。

4)非饱和风化土的相对渗透系数与土体类型与性质、预测模型、拟合参数α和n的综合影响等有密切关系。风化土相对渗透系数随着基质吸力的增大而减小；VG和Gardner预测的残积土相对渗透系数随着干密度的增大而减小，而Gardner预测的全风化土相对渗透系数曲线却呈现相反的规律；残积土和全风化土渗透系数的差异间接反映了容县花岗岩风化土边坡的渗透性质呈现上弱下强的不均匀特征，在一定程度上会影响斜坡变形破坏模式与崩岗侵蚀特征。

以上研究成果不但能为花岗岩风化土的非饱和渗流计算提供基础参数，而且将为深入分析花岗岩风化土崩岗、滑坡形成过程中的水土力学作用机制做准备。然而，本研究的脱湿试验未能获得高吸力条件下的残余段，且未探讨分析各影响因子对渗透系数及滑坡不同形成模式的影响，因此，笔者将在后续的研究中深入开展相关工作。