基于复合置信度的不确定条件下循环水系统优化

王艺慧，王彧斐*，冯 霄，韩一杰

（1.中国石油大学（北京），重质油国家重点实验室，北京 102249；2.西安交通大学，化学工程与技术学院，西安 710049;3.国能经济技术研究院有限责任公司，北京 102200）

作为化工行业中重要公用工程的循环冷却水系统，需要耗费大量的电能来维持风机和泵网络的运转以保障系统的稳定[1-2]。其用水量大约占到了工业用水量的七成。因此，循环冷却水系统的优化对于化工行业实现节能节水具有重要的指导意义。

目前循环冷却水系统的优化问题研究主要集中于优化系统的各个部件，如GOLOLO 结合冷却器网络压降、冷却塔操作、管路费用以及操作费用等多素，针对涉及多个冷却塔和冷却器的循环水系统，通过对管路和冷却器压降方程、管路费用、泵和风机的操作费用线性化，提出了一种混合整数线性规划模型，该模型可使优化后的循环水系统收益最大化[3]。SUN 等提出了1 种主辅泵网络结构，通过在指定支路上安装辅泵，使主泵压头不需要大于所有冷却器最小压头需求，从而实现泵压头减小和泵运行成本的优化[4]。CUI 等对冷却塔的喷淋系统进行了优化[5]。还有部分学者对冷却塔进行了实验研究和数值分析，提出了关于冷却塔设计的新想法，如多塔系统设计[6-7]。同时还有部分学者考虑了泵网络和冷却器网络的联合优化。SUN等提出2步法，首先将并联冷却器网络转变成串并联结构，在规定冷却器网络结构和限制水流量的基础上进行泵网络的优化，并在支管上安装辅泵[4]。

以上提及的循环水系统优化大都假设参数固定，优化后的系统存在较大的改进空间。但实际操作过程中，许多参数存在着明显的不确定性。PISTIKOPOULOS 将不确定参数分为4 类并针对一般不确定性问题建立了模型[8]；GROSSMANN 则对当前各种优化方法经历的发展问题给出了建议和解决方案[9]。CHEN等基于近10年的不确定性模型相关研究，主要介绍了3种解决不确定性的方法[10]。在这些学者的研究基础上，在具体的水资源配置问题上，王彪等假设水资源优化配置中参数波动皆服从正态分布，并在优化程序引入病毒遗传算法，以区域水资源配置效益最优和染色体年龄最大为优化目标进行配置研究[11]；李建美等采用基于参考点选择机制的遗传算法NSGA-III 求解红延河调水工程的多目标配置模型得到受水区水资源配置的Pareto优化解[12]。杜佰林等在水资源优化配置中探寻新的求解方法，将模拟退火的思想引入基本粒子群算法当中[13]。

本研究进行动态条件下系统的优化问题，选取热物流的流量为不确定性参数；就如何平衡系统经济性和安全性问题，基于工艺要求，分别为十股物流选择合适的置信度。对比分析确定条件下和基于复合置信度的不确定条件下得出的优化结果，得到了最佳网络配置。

1 问题的提出

研究了1个考虑空气冷却器和串并联冷却水网络的系统，如图1所示。

图1 循环冷却水系统结构Fig.1 Structure of circulating cooling water system

给出冷却目标后，热物流在空气冷却器中完成一次冷却后再由水冷却器进一步冷却，以达到目标温度。完成冷却任务后的高温冷却水返回到冷却塔中降温以保证循环使用，并且冷却塔中部分冷却水存在排污和蒸发损失，因此需要等量补水。本工作中，给出了10 股热物流的初始温度、目标温度和热容量。热物流首先由空气冷却器冷却到一定温度，然后由水冷却器冷却到规定量。为减少冷却水的流量，前面水冷器使用过的冷却水顺流到另一个水冷却器中，达到节水的目的。

在循环冷却水系统的管理和规划中，许多参数在整个运行期间存在着明显的动态性、复杂性以及不确定性，这些不确定性参数将会影响循环水系统模型的构建与求解。在本系统中，工艺热物流由于存在波动而使得其流量不断变化，导致空冷器和水冷器间的热负荷分配随之变化，故将热物流的流量看作不确定性参数。考虑不确定性参数后的循环水系统，目标函数相应的成为了不确定变量，由于需要合理规划冷却器的排列形式，还会存在部分整数变量，故整个问题转变成混合整数非线性问题的求解。对于不确定性优化问题的求解，采用机会约束规划构建模型并基于蒙特卡洛算法解决MINLP问题。

循环水系统以最小化总成本为目标函数，总成本是系统各部分成本的总和，包括空冷器成本，水冷器成本，泵的总成本以及冷却塔成本。具体方程为：

2 模型的建立

2.1 空冷器

在循环冷却水系统中，热物流首先经过空气冷却器进行降温，空气冷却器以环境空气为冷却介质来实现冷却过程。空气冷却器模型常数Ca：

式中，Thin(i)和Thaout(i)分别为热物流i在空气冷却过程中的进出口温度，Fh(i)为热物流i的质量流量，这是不确定性参数。Ta和Thaout(i)分别为空气冷却器i的进口空气温度和出口空气温度，Fa(i)是空气冷却器i中用以冷却热物流的空气流量。

空气冷却器i两侧热物流的温差：

即要求两侧温差应该大于空气冷却器的最小温差ΔTmin。式中，Ta为空气冷却器入口处的空气（环境）温度，影响空气冷却器的表面速度，vNF和vF分别为空气冷却器的实际表面速度和表面速度[11]。

空气冷却器的操作成本是指运行冷却器所消耗的电力成本。空气冷却器操作成本的计算：

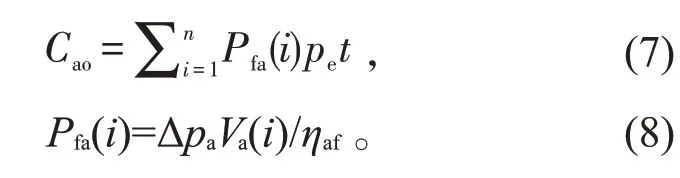
式中，Pfa(i)为空气冷却器i的风扇电力功耗，Δpa为空气冷却器风扇压降，pe为电费，t为操作时间。ηaf为空气冷却器中的风机效率。

空气冷却器风扇消耗的能量主要取决于空气冷却器的空气体积流量、风扇压降和风扇效率。Δpa的计算：

式中，ff为空气冷却器风扇的摩擦系数，Nb为空气冷却器中的管程数，Gmax表示流经空气冷却器狭窄部分时空气的最大速度，G为空气的流速，ρair为空气密度。

空气冷却器的总成本费用在计算过程中会受到不确定参数的影响，所以其在不确定条件下是变化的。

2.2 水冷器

计算水冷却器总成本时只需考虑投资成本。计算方法：

式中，dtwin(i)和d twout(i)分别为水冷却器两侧热物流与冷却水的温差，要求其应大于水冷却器的最小温差ΔTmin。

2.3 冷却水网络

为了提高冷却水的回水温度和冷却塔的效率，降低冷却水的流量，考虑采用串并联结构的冷却水网络。模型中含有一定的约束条件，用以表示进出口物流之间的关系。

Z(i,j)是一个二元变量，描述不同水冷却器之间的连接关系，表示冷却器E-i是否将出口冷却水送至冷却器E-j。每个冷却器，比如冷却器E-i，只能将出口冷却水送至下1个冷却器或将使用过的冷却水送回冷却塔中[14]：

当冷却器的冷却水来源是冷却塔中的新鲜水时，冷却器E-i的入口温度和入口水流量则为新鲜冷却水的温度和流量。当冷却器接受来自其他冷却器E-j的回用水时，此时冷却器E-i的入口温度则为E-j的出口水温，便不再接收来自冷却塔的新鲜冷却水。

冷却水总质量流量的计算：

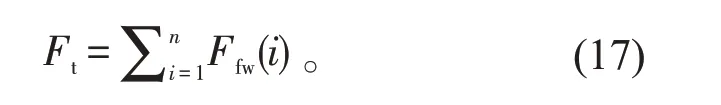
即冷却塔送至冷却器所有鲜冷却水的质量流量之和。

当计算公式中存在不确定性参数时，冷却水网络的结构可能也会随之变化，产生的费用也会不同。

2.4 泵网络

为了将冷却塔中的冷却水送至各个冷却器中，需要水泵的输送。水泵的成本计算：

2.5 冷却塔

冷却塔的总成本包括冷却塔的投资费用Ctc和冷却塔的运行成本Cto：

影响冷却塔性能和成本的因素有很多，包括局部空气湿球温度、空气湿度、大气压力、空气流量、水流量及进出口温度等。

其中冷却塔的运行成本包括风扇的运行成本、补给冷却水的总成本、排污水处理成本以及化学处理费用。在系统运行过程中，在塔底部会聚集一些矿物质和杂质，因此需要将部分冷却水排空，以保持冷却塔能正常操作运行。在工作过程中会存在部分冷却水蒸发，为保持水流量的稳定，应在系统中及时补充冷却水。冷却塔的运行成本的计算：

式中，Ctof为冷却塔的风扇费用；Ft为冷却水的总质量流量，作为本系统中重要的优化参数，水流量的减少可以显著降低冷却塔的费用；Fb和Fm分别为排污水和补给水的质量流量，二者一定程度上可以反应优化后的效果；pm是新鲜补给水的价格，t为年运行时间。

冷却塔风扇费用的计算：

式中，Qto是冷却塔的总热负荷，相当于所有水冷却器热负荷之和；cp为冷却水的比热容。

3 算法设计

选用机会约束规划方法作为求解不确定条件下优化问题的工具。它一定程度上允许所作决策不满足约束条件，但该决策应使约束条件成立的概率不小于某一置信水平α，从而保证系统的正常操作[15]。

机会约束规划模型的求解通常是在已知的置信水平和随机变量概率分布函数的条件下，通过将方程中的目标函数和约束条件转化为与确定性问题相对应的且可以运行的等价模型进行求解。为了降低计算难度，避免复杂的变换过程，采用一种新的基于蒙特卡罗算法的机会约束规划方法。Gams 软件负责目标函数的编写以及算法的调用。

根据确定条件下的流量设定波动范围，保证各流股在流量范围内的概率大于规定的置信度，运用Gams软件对这10组约束建模，得到复合置信度的不确定条件下目标函数的变化，获得优化的冷却网络配置。

4 案例研究

为验证模型的有效性，以MA等的1个案例来说明[16]。共有10 股热物流，物理参数和经济参数已知。主要考虑2 种两种情况系统的设计和优化：确定条件下的优化和基于复合置信度的不确定条件下的优化。

4.1 确定条件下的优化

表1给出了热物流流量、进出口温度和传热系数的数据。当空气温度为25 ℃，热物流特征参数固定时，得到了确定条件下的最佳循环水系统优化设计。

表1 热物流参数Tab 4 Hot stream parameters

优化后的冷却系统热物流首先经过空气冷却器冷却到一定温度，后被水冷却器冷却到目标温度，实现换热。10 股热物流进口温度相对较高，它们与空气之间的温差足以完成部分冷却任务。与仅使用水冷却器的系统相比，空气冷却器的使用减少了对循环水的需求和用量。

采用串联水冷却器结构，提高了最终回水温度，减少了循环水的用量，水冷却器最终出口温度约为55 ℃。在这种情况下，使用了9 个空气冷却器，少于水冷却器的数量，导致水冷负荷比例高，空冷负荷比例低。并且在设计过程中只考虑了经济性，不涉及水资源和环境问题，所以水冷却部分承担较多的冷却任务。

4.2 复合置信度的不确定条件下优化

实际生活中，物流在系统中的流动并不是一成不变的，往往其流量会偏离预期量。所以考虑热物流的流量为不确定性参数，热物流流量波动数据可以用均匀分布函数拟合。采用机会约束规划来解决不确定条件下的优化问题，置信水平越高说明决策的保守性越强，系统会保持更稳定更可靠的操作，但其经济性可能会不佳。机会约束规划通过量化系统盈利性和可靠性之间的关系，为决策者提供了符合约束条件的置信水平和满足经济要求的综合信息。

在考虑物流波动这一不确定性条件下，通过运行软件得到的数据可知，当物流设置的波动区间越大，较确定条件下的总成本来说，增长的越多。波动区间每增加1 个单位会造成总成本1.16%的增加。这是因为热物流流量发生变化后，经换热器冷却过程中相应的热负荷随之改变，从而增加了换热器的换热面积，影响了总成本的大小。

由于不同的物流波动对于系统的影响各异，故通过选取不同的置信度来表达流股波动程度的大小，不同的置信度会根据优化要求给出不同的输出。故基于复合置信度的不确定条件下对循环水系统进行优化。

首先，为了分析单股物流波动对优化系统所消耗的总成本的敏感性，保证其他流股流量固定，采用机会约束规划模型为所要研究的流股设定不同的置信度，运用Gams 软件分别得到10 种情况下总成本随置信度α的变化曲线，结果如图2所示。

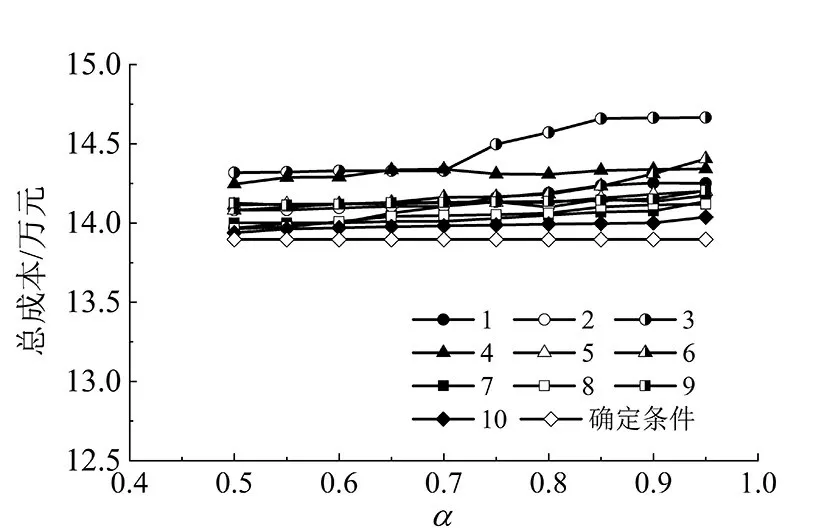
图2 10股物流波动范围内的影响Fig 2 The influence within the fluctuation range of ten streams

由图2可知，当考虑流量的不确定性时，部分物流的置信度对成本没有很大影响，曲线变化幅度不大。而有些物流的置信度会对成本产生较大影响，差值较为明显。原因在于，物流本身的流量和温度不同。对于本身温度较低且流量较大的物流来说，发生流量波动后，冷热物流间的传热驱动力较低，对系统的影响较小，总成本的变化不如高温低流量的物流明显；其次，每股物流设置的波动范围不同，一些物流在随机生成的流量范围内只发生小幅波动，造成热负荷的变化较小，因此总成本的变化没有那么明显。

通过分析10 股物流波动范围内的影响曲线，综合经济性和可靠性2 方面，分别为10 股物流选择了不同的置信度。此外，在实际工业过程中塔顶冷凝器有时会需要冷却水进行冷却，一旦冷却负荷不满足工艺要求，就会影响产品分离效果，从而对整个生产产生影响，因此面对动态的外部参数，此类物流的冷却过程需要更加稳定，故针对这类物流直接指定较高的置信度。而针对其他的产品物流，冷却负荷的波动并不会造成严重的不稳定生产，故可根据前面的分析，采用更为合适的置信度。在综合考虑图表的结果与结合实际状况后，假设第2 股物流和第10 股物流为指定置信度的物流并分别为其设定为0.95。

结合图表以及实际应用过程，分别为每股物流选出了最合适的置信度，使10 股热物流在一定的流量范围内变化且满足在指定范围内的概率大于等于选择的置信度，故得到了10 个机会约束规划的形式。在满足等式（38）的概率（Pr）约束下，对系统进行优化。

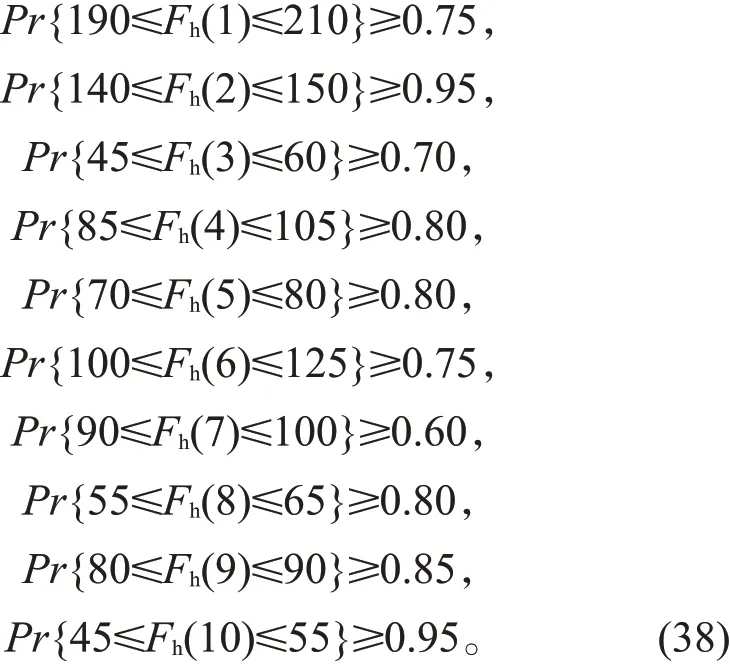
式中，Fh为热物流质量流量。

复合置信度下的优化结果包含9个空气冷却器和4 对串联的水冷却器，除了第2 股物流和第8 股物流以外，所有流股均由空气冷却器和水冷却器进行双重冷却。空气冷却器出口温度为64.9～113.6 ℃，当流股的温度高于113.6 ℃时，采用水冷却器来冷却经济性较差；在温度低于64.9 ℃时，通过空气冷却器来冷却热物流是不合适的。冷却器的排列形式与确定条件下的优化结构存在不同，部分流股仅凭借空气冷却器便能冷却到指定温度，空气冷却器的换热面积明显高于确定条件下。结果的主要差异是由于在不同的研究条件下，考虑流量的波动使得空冷器和水冷器的热负荷分配发生了改变，为实现复合置信度下的最佳优化，换热器的面积的变化引起水冷器串并联结构不同于确定条件下。此外，物流发生波动后经过水冷却器的物流出口温度降低，这也促使水冷器的换热面积减小，影响了冷却器的排列布置。

5 结果与分析

表2显示了2种案例的优化网络配置参数的计算结果。

由表2可知，优化系统的差异主要体现在水冷却器的数量、水冷却器的连接方式、冷却器的换热面积、冷却塔的总水流量等方面。这主要是因为考虑了物流流量的波动，10 股物流由于本身特性以及波动区间各异，导致在不确定条件下水冷却器和空气冷却器的热负荷分配发生了变化，从而引起换热面积的改变。同时，针对流股对系统影响程度的大小，选择不同的置信度，会比确定条件下经济效益更可观。基于复合置信度的不确定条件下的优化结果中，水冷却器的排列方式改变，仅用9个水冷却器便能完成冷却任务。且系统冷却水的用量与确定条件下相比降低6.3%。冷却塔进出口的温差变小以及用水总量的减少使得蒸发水量减少了5.4%。排污水和补充水的用量也相应减小，使得冷却塔的运行成本随之降低。

表2 2种案例的优化网络配置参数Tab 2 Optimal network configuration parameters of the two cases

为了进一步研究考虑不确定性参数的优化效果，比较了2种案例优化后的成本数据，相关结果如表3所示。

由表3可知，基于复合置信度的不确定条件下系统的总用水量低，故冷却塔的总成本费用会相应降低。虽然新的配置会引起空冷器的总成本比确定条件下高出24289.00 美元，但由于冷却塔的费用约占年度总成本费用的50%，故基于复合置信度下考虑物流流量波动可以节省107873 美元的冷却塔费用。由于水冷器排列方式的变化以及循环水用量的减小，冷却器间的压降有所降低，从而减小了水泵的总成本。因此，在循环水系统研究过程中考虑热物流流量这一不确定性参数，并根据波动效果采取不同的置信度，实现复合置信度的不确定条件下的优化，可以使每年的总成本降低10.0%。

表3 2种案例的优化成本Tab 3 The optimization cost of the two cases

综上所述，基于复合置信度的不确定性下研究循环水系统，在完成相同冷却目标的情况下，可以减少系统的总用水量，从而降低冷却塔和水泵的费用，实现节水目标。并且还可以在一定程度上减少水冷却器的数量，节约水冷却器的投资成本。除此之外，综合考虑物流波动幅度、冷却要求以及对系统的影响程度，使得不确定性下的系统在满足经济性的同时还实现了操作的稳定性，更符合工业实际运行情况，应用性更强。

6 结 论

在考虑不确定性参数存在的情况下，研究了循环冷却水系统的优化，之前的文章大多基于确定条件下展开讨论，没有涉及不确定性的问题。在这项工作中，热物流的流量是本设计中的不确定性参数，同时，由于不同物流波动对系统成本产生的影响不同、本身冷却要求各异以及设置波动范围不同，因此根据各流股特点为其选择了不同的置信度。基于复合置信度的不确定条件下，为了满足循环水系统经济合理和操作稳定的要求，采用机会约束规划建立了MINLP 模型。设计了1 种新的基于蒙特卡罗的算法，将复杂的概率约束形式转换成了Gams 软件能求解的程序，降低了计算难度[17]。在Gams 的求解汇总信息部分可以看到，DICOPT被调用来求解这个模型，共耗时397 s。

通过对比分析确定条件下和基于复合置信度的不确定性条件下循环水系统的优化配置参数，可以发现在考虑热物流流量后，流量波动会引起冷却器热负荷的变化，从而导致换热面积的改变。为平衡系统的经济性和安全性之间的关系，通过分析每股物流置信度与总成本的变化曲线，为10 股物流选择了合适的置信度。复合置信度下的循环水系统冷却器排列方式不同于确定条件下，水冷器的数量和换热面积低于后者，冷却要求主要集中在空气冷却方面。对比二者成本数据可知，基于复合置信度下考虑系统不确定性参数的优化，系统的总用水量相比确定条件下降低6.3%，水冷却器的总成本、冷却塔的总成本和水泵的成本均减小，年度总成本费用可降低10.0%，优化后的循环水系统具有良好的经济性和安全性。