一个力学结论引发的教学思考与探索
——临界速度公式的推导与应用
重庆 杨天才
1 问题呈现

图1
L
O
m
h



图2

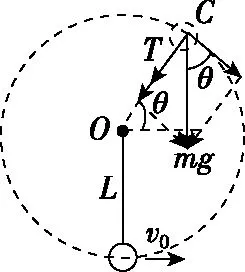
图3
2 临界速度公式的推导
做匀速圆周运动的物体应受到大小恒定的合外力F提供的向心力作用,且合外力F与速度方向垂直,始终沿半径指向圆心(如图4所示);如果物体做变速圆周运动,即线速度的大小和方向都在发生变化,其受力的特点是:合外力F的法向分力Fn,方向始终与速度方向垂直,它的作用效果只改变线速度的方向,不改变线速度的大小(即平常所说的向心力),合外力F的切向分力Fτ,方向始终与速度方向平行,它只起改变线速度大小的作用(如图5所示)。

图4

图5
长为L的轻绳一端拴一个质量为m的小球绕另一固定端点在竖直平面内做圆周运动,小球在圆心等高线上方某点C的受力分析如图6所示,显然Fn=T+mgsinθ提供向心力,只改变线速度的方向,使小球做圆周运动,Fτ=mgcosθ,提供切向力,与线速度方向相反,只改变线速度的大小,所以小球在竖直平面内做变速圆周运动,即小球从最高点A运动到最低点B,线速度逐渐变大,小球做加速圆周运动;从B运动A线速度逐渐变小,小球做减速圆周运动。只有在最高点和最低点才满足合外力提供向心力,在其他点都不成立。

图6


3 用临界速度公式解决问题
3.1 圆周运动接抛体运动问题
【例1】如图7所示,物块m(可视为质点)从半径为R的光滑固定半球面顶端无初速的滑下,求物块m脱离球面处距地面的高度。

图7


图8
3.2 抛体运动接圆周运动问题


图9


图10
3.3 自由落体运动接圆周运动问题
【例3】如图11所示,将一质量为m的小球用长为L的轻绳系住,绳的另一端固定在O点,现让绳子刚好绷直且与水平方向成30°夹角,释放小球,求小球运动到最低点时的速度大小。

图11
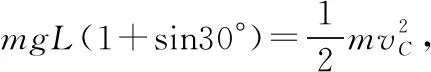


图12
3.4 等效场临界速度问题
【例4】一长为L的绝缘丝线上端固定,下端拴一质量为m的带电小球,小球所带电荷量为q,将它置于水平向左的匀强电场中,当细线偏角为θ=30°时,小球处于平衡状态,如图13所示,试求:

图13
(1)匀强电场的电场强度E;
(2)若将小球拉至右侧水平位置P处,设电场范围足够大,问小球能否摆到左侧与P等高的P′处,如果能够摆到P′处,求小球位于该处时的速度,若不能,求摆动到左侧能达到的最大高度;
(3)仍将小球拉至右侧水平位置P处,小球能否完成完整的圆周运动呢,如果不能,脱离处在哪。


图14


3.5 脱离轨道后最高点问题
【例5】如图15所示,轻质弹簧原长为2l,将弹簧竖直放置在地面上,在其顶端将一质量为5m的物体由静止释放,当弹簧被压缩到最短时,弹簧长度为l,现将该弹簧水平放置,一端固定在A点,另一端与物块P接触但不连接。AB是长度为5l的水平轨道,B端与半径l的光滑半圆轨道BCD相切,半圆的直径BD竖直,物块P与AB间的动摩擦因数μ=0.5。用外力推动物块P,将弹簧压缩至长度l,然后放开,P开始沿轨道运动,重力加速度大小为g。若P能滑上圆轨道,且仍能沿圆轨道滑下,求P的质量的取值范围。

图15




4 结束语
在解题时,凡是物体在圆心等高线上某点做圆周运动的情况,我们首先要判断物体的速度是否达到临界速度,否则物体不再继续做圆周运动,而是做斜抛运动。
学生只有了解了知识的形成过程,才能达成有意义的建构,才能达到深度思维所要求的迁移。对于竖直平面内的绳连体的圆周运动问题,既涉及运动和力的关系,又涉及功和能的变化,本文通过推导圆心等高线以上各点的临界速度,深入剖析几个典型例题,这不仅有助于提高教学效果,也有助于增强学生学习的积极性和主动性。

