FDA MIMO双基雷达主瓣走动矫正距离模糊杂波抑制
王宇卓, 朱圣棋, 李西敏, 兰 岚
(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710017)
0 引 言
双基地雷达采取收发分离的天线阵列架构,在面对“四大威胁”:电子干扰、超低空突防、反辐射导弹、隐身武器时有更高的生存能力和探测优势,将发射平台安置于敌方攻击范围外,利用飞机等设备作为接收平台在战场进行侦查,与传统单基地雷达相比,其探测的隐蔽性和生存能力都大大增强,在现代军事装备革新过程中,被多个军事强国应用于空基、天基、陆基等雷达系统[1-3]。双基地体制在发挥空间优势的同时,也面临着杂波谱分布特性更为复杂的问题(双基地雷达的杂波特性受其收发阵几何分布与速度方向的双重影响)。在单基地正侧视阵雷达架构下,不同距离的杂波在功率谱具有相同分布特性,训练样本数量充足,采用空时自适应处理(space time adaptive processing, STAP)技术[4]能够对杂波进行有效抑制。而在双基地雷达系统中,雷达杂波具有距离依赖性,即杂波分布特性随距离变化而变化,因此传统STAP方法的杂波抑制性能明显恶化,双基地雷达探测面临严峻挑战。
问题1:在无距离模糊的情况下,不同距离门的训练样本杂波分布特性不同,因此同一区域训练样本杂波呈非均匀分布[5]是双基地雷达面临的问题之一;问题2:在高重频脉冲体制下,不同距离的杂波回波在雷达进入稳态工作时,会重叠在一起。由于存在距离模糊,接收端混入了无模糊距离区和模糊距离区的杂波,但双基地雷达杂波存在距离依赖性,这两个区域的杂波特性有很大差异,严重污染了雷达观测区域,慢速目标产生的回波,将会与来自无模糊和距离模糊区域的杂波竞争,导致雷达目标检测性能下降;问题3:多输入多输出(multiple input multiple output, MIMO)双基地雷达系统杂波为发射、接收和多普勒三维空间分布,多维度意味着系统需要更多的STAP独立同分布训练样本,由于双基地雷达杂波距离依赖性,普通采样难以满足所需的样本数目,而且多维度大大提高了STAP自适应权值求解的运算复杂度。
如何克服上述3点问题,进而抑制杂波来提高雷达的检测性能,是MIMO双基地雷达迫切需要解决的问题。针对问题1(训练样本非均匀分布的难题),众多学者提出了不同方法来补偿杂波样本的距离依赖性,以满足独立同分布特性,如:时变权方案[6]、基于导数的更新方法[7]、多普勒频移(Doppler warping, DW)法[8-9]、角度多普勒补偿[10]、自适应角度多普勒补偿[11]、高阶DW[12]、联合时空插值技术[13]、基于配准的补偿技术[14]等。然而,当存在由双基地和高重频引起的多重距离模糊杂波时,上述方法不能有效解决杂波重叠问题,且因为多重距离模糊杂波的存在,不同距离门训练样本对齐的效果也会下降。
近年来,频率分集阵列(frequency diversity array, FDA)技术得以迅速发展[15-17],它通过阵列间频率增量的微调,使雷达在距离维获得了额外的自由度,FDA的这一特点在灵活波束特性、联合参数估计等方面得以具体应用[18-21]。FDA技术的引入为双基地雷达提供了距离维信息,使得距离模糊杂波的抑制变得更加灵活,有望解决双基地雷达面临的上述3点问题。
然而,无论是在相控阵FDA的发射方向图还是MIMO体制下FDA的等效发射方向图的研究中,上述文章中均未曾强调FDA体制雷达不同脉冲间发射方向图主瓣照射角度走动的问题: FDA体制下不同阵元间存在Δf的频率偏差,就同一个阵元而言,前一个脉冲和后一个脉冲相差一个脉冲重复间隔(pulse repetition interval, PRI)时长设为T,导致的相位差φ=ΔfT,不同于传统相控阵发射方向图主瓣不变,FDA体制发射方向图是距离(时间)-角度耦合的,因此积累的相位差导致不同脉冲间发射方向图主瓣照射的角度不同,雷达无法相干积累,更不能进行空时二维处理。传统研究FDA方法的大部分研究均未考虑发射方向图主瓣走动的问题,而多是关注接收后的信号处理方法,或是侧重研究单脉冲和连续波体制下FDA雷达方向图距离角度二维耦合特性。采用多脉冲空时二维自适应处理方法时,如何解决FDA雷达体制下发射方向图主瓣走动的问题,将关系到雷达是否能够正常工作。
针对双基地雷达距离模糊杂波和FDA体制脉间发射方向图主瓣走动的问题,本文将讨论一种新的正侧视阵双基地雷达距离模糊杂波抑制方法,该方法将传统双基地MIMO雷达发射空间角频率,接收空间角频率和多普勒空间三维搜索拆分为先在发射维和多普勒二维搜索,并进行距离模糊杂波抑制,在得到目标发射角度和多普勒信息后,再在接收空间进行降维搜索,即三维搜索拆分为“2+1”的搜索形式。首先,在发射角度和多普勒二维域内,通过在发射端阵元相位加权,抵消阵元因不同脉冲间隔T导致的相位差φ=ΔfT,其次在接收端经过反补偿,消除发射端加权对信号参数的影响。不同于传统FDA雷达和MIMO雷达杂波在功率谱呈现固定的几何分布关系,该方法使非观测区域杂波在功率谱具有低增益离散分布的特性,之后利用其杂波分布特性,通过信号距离耦合相位补偿和DW技术,去除距离模糊区域的杂波,同时对无模糊区域杂波进行补偿对齐。然后,通过杂波自适应抑制,搜索目标的发射角度和多普勒信息,最后再利用上述信息构造降维矩阵,在目标接收角度域进行搜索。通过与传统方法对比,证明了该方法在双基地距离模糊杂波抑制方面的有效性。
该方法的创新之处总结如下:
(1) 针对传统FDA雷达发射方向图主瓣走动的问题,提出FDA-MIMO雷达接收端等效发射方向图主瓣矫正方法,使不同脉冲信号的主瓣均照射在同一角度,能够完成信号脉冲间的相干积累,在此基础上能实现多脉冲FDA体制雷达的正常工作。
(2) 针对双基地距离模糊杂波问题,通过FDA-MIMO雷达等效发射方向图主瓣矫正补偿和接收到信号后的反补偿处理,该方法使得不同距离的杂波因距离耦合的相位项实现相互区分。不同于传统双基地MIMO雷达和双基地相控阵雷达的距离模糊杂波在功率谱内呈固定的几何分布关系,本文方法使功率谱中观察区域内的目标信号与杂波保持高增益,而非观察区域的距离模糊杂波呈现低增益离散分布,对其进行抑制并结合杂波距离依赖性补偿技术实现目标参数搜索。
(3) 针对MIMO双基地雷达三维杂波结构训练样本不足和自适应权值求解运算量大的问题,本文将三维搜索拆分为“2+1”的形式,先在发射角频率域和多普勒域对杂波进行抑制并进行目标参数搜索,再根据得到的目标发射角度和多普勒信息构建降维矩阵,在接收角频率域进行降维搜索,最终得到目标参数。
1 FDA-MIMO双基地雷达主瓣矫正补偿信号模型
图1为距离模糊杂波区域分布图,绿色箭头所指为机载雷达发射阵列的主瓣,在主瓣照射的地面区域内,蓝色表示观察区域,区域内黑色点表示雷达搜索期望目标的位置,斜距RΣ=R0为发射和接收阵列到期望目标距离之和,橙色表示非观测的距离模糊区域,区域内灰色点表示与期望目标位置相对应的距离模糊区域位置,其对应的斜距分别为RΣ=R1=R0+Ru,RΣ=R2=R0+2Ru,其中Ru=c/fPRF为最大不模糊距离,fPRF为脉冲重复频率(pulse repetition frequency, PRF)。
机载正侧视阵FDA-MIMO双基地雷达收发阵列的几何关系如图2所示。

fm=f0+(m-1)Δf,m=1,2,…,M
(1)
式中:Δf是频率增量,(m-1)Δf表示第m个阵元相对于f0的频率差,且Δf≪f0。与传统相控阵雷达类似,FDA-MIMO雷达的第m个阵元发射的窄带信号可以表示为
(2)
式中:rect(·)是矩形窗口函数,表示一个信号脉冲;Tp表示脉冲宽度;sm(t)是对应于第m个阵元的正交波形。当满足理想正交条件时,有
(3)
当式(2)发射的信号到达远场时目标接收的窄带信号表示为

(4)

图3展示了发射阵列阵元在3个脉冲中对应的相位累积情况,以及不同脉冲对应的等效发射方向图主瓣照射角度分布情况。不同脉冲间在PRI对应时间T内由于Δf的相位积累量φ=ΔfT,使脉冲间有不同的发射初相,而FDA雷达发射方向图具有距离(时间)-角度耦合性[22],因此不同脉冲对应的接收端等效发射方向图主瓣照射的角度会走动,图中具体显示了在发射角度和距离二维域3个脉冲主瓣的走动情况,脉冲宽度设为4.7e-05 s,对应的距离为14.1 km,PRI为6.6e-04 s,对应距离为200 km,Δf=1/2fPRF,从图中看出第1个和第3个脉冲,分别位于600 km和200 km处,主瓣高增益照射区域一致为30°到0°,位于400 km处第2个脉冲主瓣方向为-20°~-90°以及70°~90°。因此,脉冲间的回波为不同角度位置目标反射的回波,不能相干叠加,无法杂波相消或者空时二维处理。
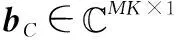
d(Δf/fPRF)= [0,-j2πΔf/fPRF,…,-j2π(M-1)Δf/fPRF]T
(5)
hK1=[0,1,…,K-1]T
(6)
bC=exp{hK1⊗d(Δf/fPRF)}
(7)

图4为等效发射方向图主瓣走动矫正后的示意图,图中通过发射端加入主瓣矫正权值矢量bc,在不同发射脉冲间施加一段相位负延迟(图中红色部分所示),抵消图中的相位累积量,使不同脉冲方向图均照射相同角度范围,图中脉冲内蓝色虚线为经过主瓣走动矫正后的方向图3个脉冲主瓣位置示意图。
通过式(7)对雷达进行主瓣走动矫正后,式(4)变为
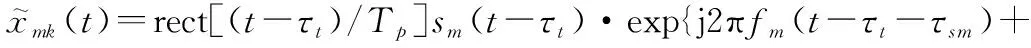
(8)
接收到远场反射信号回波后,第n个阵元接收的第k个脉冲的信号表示为
(9)

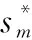

(10)

(11)
因为Δf≪f0, FDA表达式中包含Δf的相位项可以简化[23]为
fm=f0+(m-1)Δf≈f0
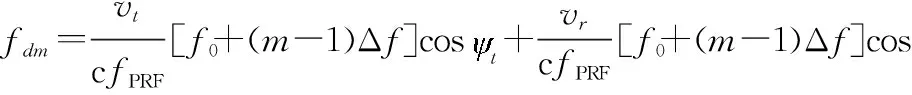
式(11)可以表示为
(12)
相干处理脉冲数为K,接收阵元发射阵元分别为M和N,接收信号的空时快拍表示为
(13)
sd(fd0)=[1,exp{j2πfd0},…,exp{j2π(K-1)fd0}]T
(14)
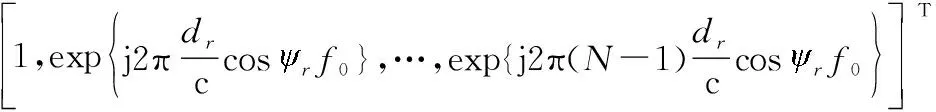
(15)
复合发射导向矢量表示为
sc t(fc t)=sR(fR)⊙st(ft)
(16)

sR(fR)=
(17)
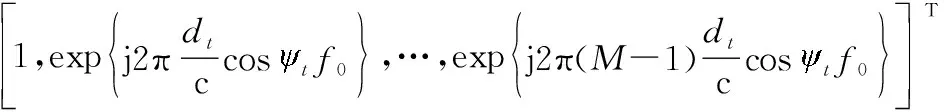
(18)
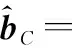
(19)
2 FDA-MIMO双基地距离模糊杂波抑制方法
在普通MIMO双基地雷达中,接收信号回波功率谱在发射角频率、接收角频率和多普勒域内呈现三维分布的特性,因此在功率谱扫描的时候面临两方面的问题:一是算法复杂度大,即N3M3K3,难以实时计算;二是计算自适应权值时,要求满足独立同分布样本的数量大于等于二倍的自由度,对于实际的双基地雷达回波而言难以获取满足数量要求的样本。上述两个问题使得MIMO双基地雷达难以自适应滤波,同时双基地雷达距离模糊杂波在功率谱的叠加以及杂波的距离依赖特性,均为杂波抑制提出难题。因此,本文提出一种基于FDA-MIMO的双基地雷达主瓣矫正距离模糊杂波抑制方法,利用FDA技术实现距离模糊杂波抑制,同时将发射空间角频率、接收空间角频率和多普勒空间三维搜索拆分为先在发射维和多普勒二维搜索,再在接收空间角频率域进行的搜索,即三维搜索拆分为“2+1”的搜索形式。
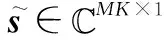
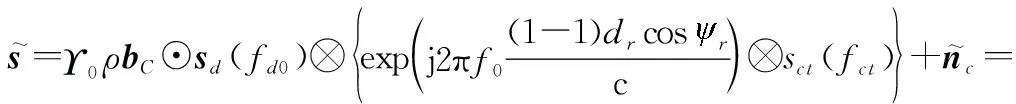
(20)
由式(20)可以看出,信号回波包括多普勒频率和发射空间角频率,由于FDA雷达发射空间角频率中含有距离耦合的相位项sR(fR),接收通道接收的总的杂波回波矢量可以表示为
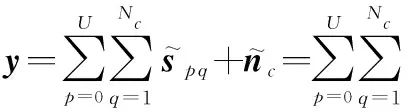
(21)
式中:U表示威力范围内距离模糊区域总数(其中p=0表示无模糊区域);Nc表示同一距离环内杂波块总个数。
图6为第一模糊区域(R1)杂波与无模糊区域(R0)杂波的时域脉冲回波示意图,蓝色矩形表示无模糊区域的信号和杂波回波,桔色表示第一模糊距离区域的回波,回波编号和发射脉冲的编号相对应。可以看出在接收端不同区域的距离模糊杂波重叠在一起,式(21)中的加和符号表示两种回波在接收端被同时接收。
针对不同的模糊或无模糊区域,利用二次距离补偿方法[24],对发射空间导向矢量进行相位补偿,构造距离相位补偿导向矢量:
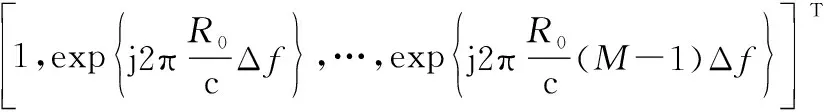
(22)
eR(fR0)=gK1⊗qR[fR(R0)]
(23)

(24)
一次距离模糊区域回波信号写为

(25)
式中:R1=Ru+R0,Ru=c/fPRF。如图6所示,式(24)中与式(25)中第k个脉冲对应的主瓣发射矫正补偿序数分别表示为k-1和mod5|(k-1)+4|,因其回波在接收端相互重叠,所以距离模糊区域脉冲回波与无模糊区域脉冲回波相差一个序号。总回波信号经过二次距离补偿后,无模糊区域和一次距离模糊区域信号依然含有等效发射方向图主瓣矫正补偿项,下面就发射矫正项进行还原补偿。构造与主瓣矫正权值相应的矫正还原补偿矢量:
d(Δf/fPRF)=[0,j2πΔf/fPRF,…,j2π(M-1)Δf/fPRF]T
(26)
bRC=exp{hK1⊗d(Δf/fPRF)}
(27)
式中:hK1=[0,1,…,k-1]T,将其代入式(24)和式(25)进行补偿,无模糊区域回波信号写为

(28)
一次距离模糊区域回波信号写为

(29)
由于Ru=c/fPRF,一次距离模糊区域回波式(29)可以进一步写为

(30)

图7为前视阵空时杂波功率谱示意图,显示了3个采样距离门在无模糊区域(R=R0,图中为实线表示)和第一距离模糊区域(R=R1,图中为虚线表示)的杂波回波曲线,其中黑色-蓝色-红色分别表示同一区域斜距由小到大的3个距离门。观察图7(a)可以看出,传统MIMO雷达多普勒频率和发射角频率在功率谱中有固定的几何关系,杂波呈曲线形状分布,而本方法的杂波回波如图7(b)所示,无模糊区域杂波回波与传统MIMO相同,第一模糊区域回波由于存在与Δf和fPRF相关的相位项,因此多普勒频率和角频率的几何关系不再固定,同一距离R1不同角度对应的杂波块回波在角度域和多普勒域的位置无固定的几何关系和分布形状,呈低增益的离散分布,因此通过补偿,在保持无模糊距离区域信号回波高增益的情况下,使距离模糊区域回波呈现低增益的离散分布,从而起到距离模糊杂波抑制的效果,之后,信号处理方式与传统MIMO雷达类似。在雷达多输入单输出(multiple input single output, MISO)阶段,选取一个接收阵元的数据,将原本NKM三维数据经过降维得到MK维数据,抑制距离模糊杂波后再使用DW等方法将杂波脊进行对齐补偿,从而减小无模糊区域不同距离门杂波的距离依赖性对自适应权值的影响,最终实现前视阵雷达距离模糊杂波抑制。结合式(21)、式(23)和式(27),接收端总补偿表达式表示为
(31)
式中:距离补偿项eR(fR0)通过哈达玛⊙与发射导向矢量距离耦合相位项相乘,使发射导向矢量距离耦合频率fR(pRu/c)为距离模糊区域数p耦合的项,过程如式(24)、式(25)所示,之后再与主瓣矫正补偿矢量bC对应的频率项fbC和矫正还原补偿矢量bRC的频率项fbR C相乘,过程如式(28)、式(30)所示,得到αp耦合的相位项,其与模糊区域数相关。
通过上述步骤,再使用传统STAP方法对双基地的发射角度域和多普勒域进行扫描,得到目标的发射角度和多普勒两个维度的信息,下一步再估计接收角度。根据上一步得到的发射角度和多普勒频率参数构造多波束矢量:
T=dT⊗bT⊗aT
(32)
式中:
(33)

(34)
式中:WT=THW;ST=THS;RT=THRT。通过将原本MIMO双基地雷达回波的三维结构拆分为“2+1”的形式进行搜索,减小了双基地杂波距离耦合性对于传统STAP算法的影响,减小了训练样本数量的要求,降低了自适应权值计算的算法复杂度。同时FDA雷达抑制了距离模糊杂波对雷达探测区域的污染,使得双基地雷达有更优的参数估计能力。整个FDA-MIMO双基地雷达的系统处理流程框图如图8所示。
3 仿真实验与对比讨论
本节将对所提出的方法进行模拟仿真,并与其他方法进行比较。首先,针对不同距离模糊区域,对不同雷达结构下的回波功率谱进行了仿真比较。其次通过雷达改善因子(improved factor, IF)指标,对比不同方法距离模糊杂波抑制的效果和降维搜索效果。最后通过不同训练样本数目下各个雷达的性能对比,说明本文方法的有效性。仿真参数如表1所示。

表1 双基地雷达仿真参数
图9显示了主瓣校正补偿前后FDA MIMO雷达的等效发射方向图,其方向图有距离角度的耦合性,因此主瓣在角度距离二维区域呈现S型,图中期望信号位置为0°,显示了连续3个脉冲周期的方向图主瓣分布情况,脉冲宽度为4.7e-05 s,对应距离为14.2 km,脉冲重复间隔为6.6e-04 s,对应距离为200 km,观察图9(a)可以看出,第一个脉冲周期方向图主瓣高增益角度位于0°~30°之间,由于FDA MIMO雷达不同阵元间载频不同,经过一个PRI的积累后,在发射第二个脉冲时,各个阵元的初相不同(如图3所示,第m个阵元积累初相为2π(m-1)ΔfT),再加上FDA MIMO方向图具有S型距离角度耦合分布特性,因此在第二个脉冲周期时方向图主瓣高增益角度位于-23°~-110°,由于角度周期性,在图中[-90°,-110°]显示在[70°,90°]位置。仿真中Δf=1/(2T),因此在第3个脉冲周期时,第m个阵元积累初相为2π(m-1)Δf2T=2π(m-1),各个阵元初相相同,因此与第一个脉冲周期情况相同。图9(b)为FDA MIMO雷达经过主瓣校正补偿后的等效发射方向图,由式(7)可知,第一个脉冲周期初相补偿为0,因此与图9(a)相同,第二个脉冲周期第m个阵元补偿量为-2π(m-1)ΔfT,与Δf积累初相相同,因此其方向图与第一个脉冲周期的相同,同理第三个脉冲周期经过补偿也与第一个脉冲周期一致。
图10(a)和图10(b)分别为传统MIMO和主瓣矫正FDA双基地雷达在多普勒和发射角度维的CAPON扫描功率谱,仿真中在无模糊区域RΣ0=60 km和第一距离模糊区域RΣ1=183 km处均有杂波回波。由于双基地雷达几何位置的分布,因此杂波呈斜曲线分布,图10(a)为传统MIMO雷达杂波功率谱,可以看出杂波具有距离依赖特性,不同距离的杂波回波形状不同,虽然两处距离的杂波重叠在一起,但是在归一化发射角频率ft=0.2和归一化多普勒频率fd=0.15附近能看出因不同模糊区域杂波形状不同而存在的凹陷。图10(b)是本文方法的杂波谱,图中仅呈现出无模糊区域RΣ0的杂波,通过两次补偿,此时位于ft∈[-0.6,0.6]区域内的杂波回波来自我们所关心的无模糊区域,通过对比观察可以看出,第一模糊区域的杂波增益被抑制。对比图10(a)的传统双基地雷达,本文方法能实现不同区域距离模糊杂波的完全分离,与传统FDA雷达相比,不同分离效果不受雷达参数影响,并具有有效的抑制效果。
由于距离模糊杂波的存在,传统双基地雷达重叠杂波的频谱在发射空间和多普勒频率域内严重展宽,导致目标检测性能下降。图11是对应于归一化角频率ft=0.16的杂波谱的IF曲线。IF曲线是用于评估雷达有效性的指标,其定义为输出和输入的信噪比之比:
(35)
式中:s表示信号矢量;w表示接收端导向矢量权值;Q为噪声协方差矩阵。
观察图11可以看出,本文的方法对问题有了实质性的改进。观察两雷达DW补偿前的IF曲线可以看出,由于无模糊区和第一模糊区的杂波回波,MIMO雷达IF曲线在-0.22和0.18处有两个凹口,其中-0.22处的凹口是由无模糊区杂波引起的,0.18处是由第一模糊区域距离模糊杂波引起的,距离模糊杂波具有距离依赖性,因此不同区域的两处杂波脊形状不同,相互叠加。从图中可以看出,雷达的多普勒域检测性能在杂波凹口处及其周围位置存在严重下降,因此,杂波凹口越多,污染的检测区域越大。对于传统的MIMO双基地雷达,由于杂波距离依赖性和不同区域距离模糊杂波重叠的影响,其性能明显下降。而本文的方法抑制了非观测区域外的模糊距离杂波,观察红色虚线可以看出,FDA双基地雷达IF曲线只有一个-0.22处凹口,这是由无模糊区域内的杂波引起的,性能损失凹陷宽度小于MIMO方法。结果表明,该方法能显著降低雷达距离模糊杂波在功率谱中的重叠现象,抑制距离模糊杂波。图中实线为经过DW方法补偿后的雷达IF曲线对比图,蓝色为经过DW方法补偿后传统MIMO双基地雷达的IF曲线,由于距离模糊杂波的存在,无模糊区域杂波(fd=-0.22)和距离模糊区域杂波(fd=0.18)依然存在重叠现象,补偿的结果使无模糊区域杂波展宽现象被抑制,经过DW补偿后曲线凹口位置由原来的0.18变为0.16,其IF曲线依然存在两处凹口,且凹口之间的区域性能也同样受其影响。而红色的主瓣矫正FDA-MIMO双基地雷达IF曲线,由于距离模糊杂波被抑制,因此仅有一处凹口的IF曲线经过DW方法补偿后,杂波展宽被抑制,对比MIMO双基地雷达,其探测性能得到明显改善。
图12为MIMO双基地雷达无模糊区域杂波脊在发射角度域、接收角度域和多普勒域的三维空间结构图,选取红绿蓝黄4种颜色分别表示距离由近到远的距离门对应的杂波脊。在前面双基地MISO阶段,通过杂波抑制和自适应搜索已经得到目标的多普勒、发射角度信息,根据二维信息,我们依据式(32)和式(33)构造降维矩阵对MIMO双基地雷达的三维结构进行降维搜索。图13为MIMO双基地雷达三维结构中发射角频率ft=0.16时杂波的多普勒-接收角度二维域CAPON功率谱图,其可以看作图12三维结构在发射空间域ft=0.16处的切片,横坐标为归一化接收角频率域,纵坐标为归一化多普勒频率域。再结合期望目标的多普勒信息,我们对三维的MIMO双基地雷达信号进行降维搜索,并和传统3DT降维方法进行对比。
图14表示训练样本数目分别为300和500时,本文降维搜索方法和传统3DT降维方法性能的IF曲线对比图,横坐标为归一化多普勒频率,纵坐标为功率,并在图中标出理想全维自适应方法在充足训练样本时的性能曲线作为参考(依据RMB准则理想训练样本数为1 536)。观察可以看出,在两种不同样本数目情况下,本文降维方法和3DT降维方法在杂波存在(归一化多普勒频率fd=0.24)处有相同探测性能,均小于理想情况,而在其他多普勒位置,本文方法均优于3DT降维方法,相比之下和理想情况的曲线更加接近,同时注意到随着样本数的增加,3DT性能和本文方法的差距减小。图15遍历了训练样本数目在[300,800]范围内,位于ft=0.16,fd=-0.56,fr=-0.288处不同方法对应的IF值,图中横坐标为样本数,纵坐标为对应IF值,本文方法和3DT降维方法、普通全维自适应方法分别用红色、紫色、蓝色表示。可以看出在样本数远低于二倍雷达自由度的情况下普通全维自适应方法的雷达探测性能最低,本文方法和3DT降维方法性能随着样本数的增加而增加,且在样本数不变的情况下本文方法均优于3DT降维方法,此结果与图14结果一致,因此从图15可以看出在训练样本数稀少的情况下,3种方法中普通全维自适应方法性能最低,其次是3DT降维方法,本文方法最优。
4 结 论
本文介绍了一种FDA雷达脉间主瓣走动的矫正算法,并提出了一种距离模糊杂波抑制方法。针对MIMO双基地雷达回波的三维结构,将三维数据拆分成二维和一维数据分别进行处理,在二维的MISO阶段,FDA-MIMO雷达在发射端通过主瓣走动矫正相位加权,使不同脉冲的主瓣照射区域相一致,然后在接收端进行恢复补偿。由于FDA信号回波的距离耦合特性,可以区分不同距离模糊区域的信号。通过补偿,观测区域的信号与传统的MIMO信号相同,而来自非观测区域的距离模糊信号在功率谱中呈现低增益离散分布,从而达到抑制距离模糊杂波、提高雷达探测性能的目的。之后再与相应的降维方法相结合,利用MISO阶段扫描得到的发射角度和多普勒信息构造降维矩阵,在接收角度域进行降维搜索,在双基地雷达独立同分布训练样本不足的情况下,改善了传统STAP方法的探测性能,仿真结果证明了该方法的有效性并与传统方法进行对比。需要强调的是,该方法适用于一般阵列几何。
未来进一步研究需要考虑的领域包括扩大FDA在双基地雷达中应用的策略、提高距离、角度和多普勒域目标参数估计精度以及拓展高分辨率成像观测等功能。需要注意的是, FDA-MIMO双基地雷达在正交波形不完全正交和目标反射系数的实际误差会导致性能下降,这将对未来的研究方向产生影响[25-28]。

