基于Mathematica的弹簧摆内共振现象研究*

赵文丽 张 红 厉桂华 高 峰

（山东农业大学信息科学与工程学院 山东 泰安 271018）

1 引言

弹簧摆是由轻质弹簧和悬挂的小球构成，在铅直平面内运动的弹簧可以看成是一个双自由度振动系统，是典型的非线性运动之一.关于弹簧摆的混沌行为引起了人们的广泛关注［1～6］.这些报道从理论求解、数值分析和计算机模拟等方面对弹簧摆的运动作了一定的研究.弹簧摆的运动可以分解为振动和摆动两种模式的合成，对应于这两种运动模式有两个固有频率，当这两个频率满足一定条件时，两个振动模态强烈地耦合，一种振动会激发另外一种振动，这种现象就是弹簧摆的内共振现象.本文从系统的动力学方程出发，利用Mathematica数值计算和模拟功能描绘了弹簧摆运动的轨迹图、振动曲线和能量曲线，从而使得弹簧摆的运动更加直观.

2 弹簧摆的动力学方程

如图1所示，弹簧摆是由质量忽略不计的轻质弹簧与悬挂着的质量为m的小球构成.弹簧劲度系数为κ，原长为l0，弹簧的瞬时长度为l，小球的直径可以忽略不计.取O点为摆球的平衡位置，沿水平方向为x轴，竖直方向为z轴，建立直角坐标系.系统的势能为

图1 弹簧摆

根据式（1）可以得到系统的动力学方程为

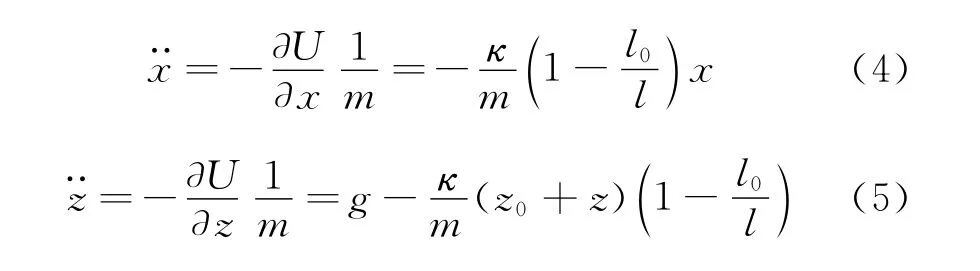
理论上来讲，求解式（4）和式（5）构成的方程组，就可以分析弹簧摆的运动行为，而实际上，这两个方程没有严格的解析解，研究该体系的动力学行为需要对这两个方程进行数值计算.

3 弹簧摆内共振的Mathematica仿真

数学软件Mathematica具有强大的数值计算功能［7］，利用Mathematica的NDSolve命令可以在不作任何近似的情况下直接求得弹簧摆的动力学微分方程（4）、（5）的数值解.考虑到小球运动速度不大，可以认为过程中阻力与速度成正比，因此对方程（4）、（5）修正如下

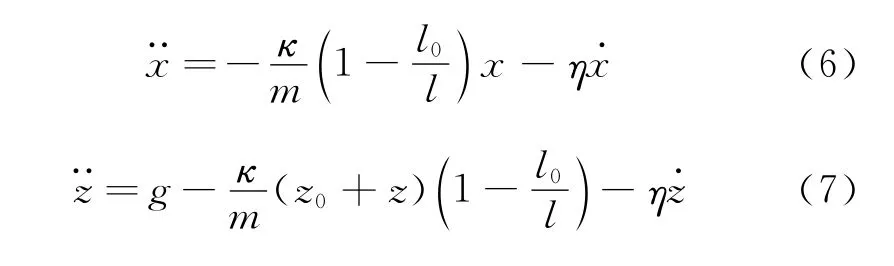
其中η是阻力系数，这主要考虑的是空气摩擦阻力.为了检验数值计算的精确性，计算中直接选取文献［6］中的实验数据，m=4.86×10-2kg，κ=2.30 N／m，z0=0.82 m，此时，ωp=3.46 rad／s，ωs=6.89 rad／s，满足内共振条件.两种不同的初始条件为

初始条件1：x（0）=14.1 cm，z（0）=10.9 cm（对应于小摆幅振动）

初始条件2：x（0）=19.6 cm，z（0）=5.74 cm（对应于大摆幅振动）

分别在两种不同的初始条件下考察弹簧摆运动轨迹、两个方向的位移和能量随时间的变化.

图2为弹簧摆的运动轨迹，结果显示初始条件不同，轨迹所形成的轮廓不同，弹簧摆的运动范围不同，表明弹簧摆的实际运动轨迹取决于初始条件.但是无论对应哪一种初始条件，弹簧摆的伸缩摆动都只能在一定的空间范围内，其活动范围都是有界的.

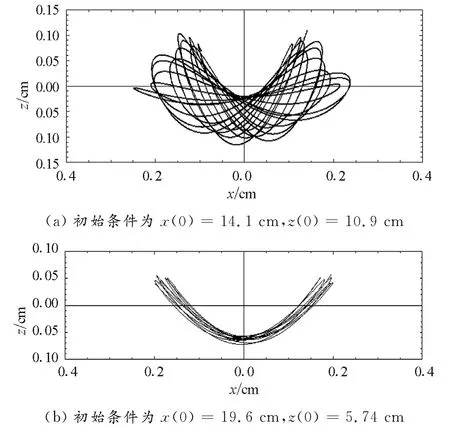
图2 弹簧摆在不同初始条件下的运动轨迹

图3和图4是两种初始条件下两个模态的振动曲线，从图中可以看出，弹簧摆无论是做小摆幅摆动还是做大摆幅摆动，x模态和z模态都有倍频关系的内共振现象，但是唯有小摆幅的振动，才有强烈耦合的情形.由图3（b）可以看出，当在z方向的振幅趋于零时，z模态的相位发生了突变，而x模态的相位是连续的.这些现象都与文献［6］中的实验结果一致.

图3 初始条件为x（0）=14.1 cm，z（0）=10.9 cm下的振动曲线及相位情况

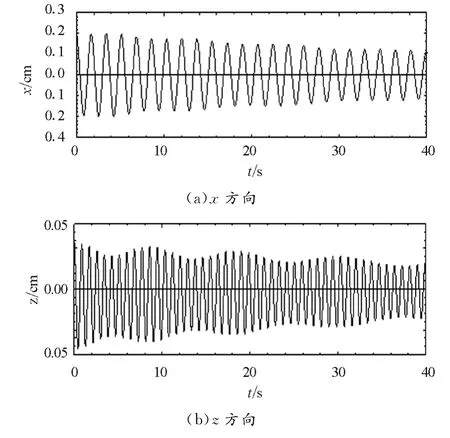
图4 初始条件为x（0）=19.6 cm，z（0）=5.74 cm下的振动曲线及相位情况

由于我们只关心各能量之间的相对关系，而振动系统的能量与振幅的平方成正比，所以可以用振幅的平方代替能量.图5和图6画出了不同初始条件下两种模态能量随时间的变化曲线，需要说明的是，图（5）和图（6）中的纵坐标实际上是振幅的平方.

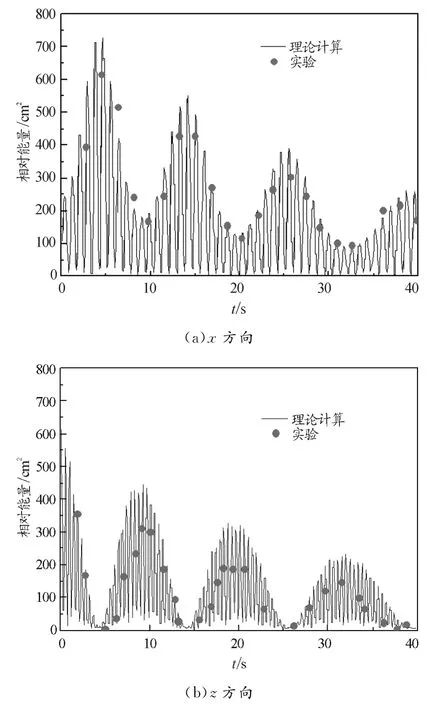
图5 初始条件为x（0）=14.1 cm，z（0）=10.9 cm下的相对能量

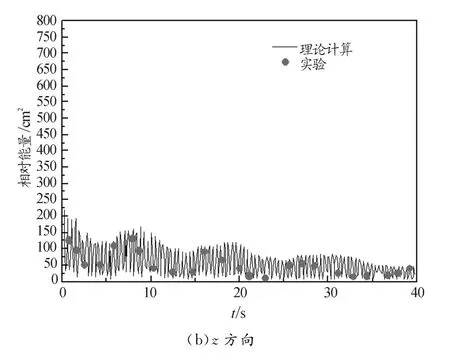
图6 初始条件为x（0）=19.6 cm，z（0）=5.74 cm下的相对能量

由图（5）和图（6）可知，随着时间的推移，能量在两个模态之间不断传递和转换，因为有阻力的存在，能量并不守恒，总能量逐渐减小.在初始条件1的振动中，两个模态的能量变化幅度较大，而在初始条件2的振动中，能量的变化幅度则相对较小，能量曲线相对平缓.图中黑色曲线为理论模拟结果，点为文献［6］的实验值，可以看出，两种实验条件下，理论值和实验值都吻合得非常好.

4 结论

本文应用一种弹簧摆系统模型，通过计算机数值模拟方法分析了弹簧摆的内共振现象，通过描绘运动轨迹和振动曲线，将弹簧摆的运动特征直观地呈现出来，数值模拟结果与实验结果表现出高度的一致性，再一次验证了应用Mathematica对系统动力学数值仿真的正确性与可靠性.