钢筋非均匀锈蚀导致混凝土开裂的研究

刘继睿，商怀帅，王玮钊，李树良，胡忠存

(青岛理工大学 土木工程学院，青岛266525)

钢筋混凝土内部钢筋锈蚀产物体积是原锈蚀钢筋的2～4倍[1]。锈蚀产物体积膨胀将导致混凝土保护层开裂，裂缝的存在加速有害物质对钢筋的侵蚀，进一步促使锈蚀的产生。锈蚀产物及保护层裂缝对钢筋及混凝土间黏结性也将产生不利的影响，破坏钢筋与混凝土协同工作的前提。钢筋锈蚀导致保护层开裂是影响钢筋混凝土结构耐久性及承载力的重要因素。因此确定混凝土保护层开裂时的钢筋锈蚀程度及开裂后钢筋锈蚀程度与保护层裂缝宽度之间的关系尤为重要。

对于钢筋锈蚀导致混凝土开裂的研究已有很多，这些研究可以划分为3个类型：试验、解析、模拟。在试验研究中大多采用通电加速锈蚀来到达缩短试验时间的目的，ALONSO等[2]通过试验研究了混凝土保护层裂缝宽度与钢筋锈蚀深度之间的关系，并建立两者之间的线性函数；KIM等[3]通过试验分析锈胀裂缝的开展；NABI等[4]通过试验对锈蚀开裂时间做出研究。理论解析层面上为简化计算，大多采用均匀锈蚀模型，CHERNIN等[5]将保护层简化为厚壁圆筒提出均匀锈蚀下开裂预测模型；ZHANG等[6]建立了初始缺陷下的锈蚀开裂模型。数值模拟上多采用有限元方式计算锈蚀开裂，DU等[7]通过有限元模拟分析锈蚀开裂及裂纹的发展；SANZ等[8]建立膨胀连接单元来对锈蚀产物的体积膨胀进行模拟；涂熙等[9]通过格构式模型对锈胀力引起的混凝土开裂进行模拟。

但之前的研究大多是基于钢筋横断面上的锈蚀是均匀的前提下进行的，未考虑钢筋锈蚀的不均匀性。而在实际情况下，混凝土中的钢筋锈蚀是非均匀的，往往是靠近保护层一侧锈蚀率较高，而背离保护层一侧锈蚀率较低。本文将根据锈蚀三阶段模型，基于钢筋的非均匀锈蚀，应用弹性力学理论，对锈蚀导致混凝土保护层开裂时的钢筋锈蚀深度及开裂后的裂缝发展做出预测模型。

1 钢筋非均匀锈蚀三阶段模型

1.1 锈蚀三阶段模型

钢筋混凝土内钢筋从脱钝开始锈蚀到保护层开裂主要经历3个阶段[10]：①铁锈填充混凝土孔隙阶段。此阶段钢筋的锈蚀产物填充在钢筋与混凝土交接面的混凝土孔隙中，钢筋的锈蚀不引起内力的变化；②锈胀力发展阶段。当混凝土内孔隙被锈蚀物填充满后，进一步的钢筋锈蚀膨胀将引起在钢筋与混凝土交界面上的锈胀力，此阶段锈蚀产物外轮廓与混凝土保护层内轮廓相接触并保持变形一致；③混凝土保护层开裂阶段。钢筋锈蚀膨胀最终将引起混凝土保护层的开裂，开裂后将有部分铁锈会对裂缝进行填充。

根据锈蚀三阶段模型，钢筋的锈蚀深度将由三部分构成：填充混凝土孔隙对应的锈蚀深度δ1；锈胀力发展阶段对应的锈蚀深度δ2；保护层开裂后对应的锈蚀深度δ3。其中第1阶段独立于其他2个阶段的计算，第2、第3阶段由于混凝土保护层开裂状态的不同而采用不同的计算模型。因此钢筋的总锈蚀深度δmax按式(1)计算：

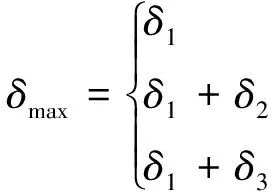
(1)

3个式子分别对应3个不同锈蚀阶段的钢筋总锈蚀深度。

1.2 孔隙填充阶段δ1计算

在铁锈填充混凝土孔隙阶段，钢筋的锈蚀深度主要取决于混凝土内部孔隙的大小和数目，这与混凝土的配合比及养护状况有关。LIU等[10]假定在钢筋与混凝土交界面上存在12.5 μm厚的多孔待填充区域，在锈蚀产生膨胀压力前必须填充满锈蚀产物。非均匀锈蚀孔隙填充模型如图1所示，根据几何关系可得待填充区被填满时的锈蚀深度：

图1 非均匀锈蚀孔隙填充模型

(2)

式中：m为填充区域厚度；n为锈蚀膨胀率；P为填充区混凝土的孔隙率，根据文献[11]的研究取P=12%。

1.3 锈胀力发展阶段δ2计算

1.3.1 钢筋锈蚀非均匀分布特征

钢筋锈蚀引起混凝土的开裂不仅与钢筋的锈蚀率有关，而且与钢筋的锈蚀分布有关。国内外的研究表明混凝土中的钢筋锈蚀多为不均匀的。锈蚀的主要分布特征为面向保护层一侧锈蚀较严重，而背离保护层一侧的锈蚀较轻。YUAN等[12]的试验表明混凝土锈蚀开裂前的锈蚀产物仅分布在面向混凝土保护层侧钢筋的半圆周上，且分布呈半椭圆形。ZHAO等[13]提出了模拟钢筋锈蚀层不均匀分布的高斯函数模型。由于混凝土保护层开裂时背离保护层一侧钢筋锈蚀率很小，本文的钢筋锈蚀模型采用假设如下：①不考虑背离保护层一侧钢筋的锈蚀；②面向保护层一侧钢筋锈蚀后轮廓为椭圆形；③锈蚀产物体积正比于被锈蚀钢筋体积。钢筋非均匀锈蚀形态如图2所示。

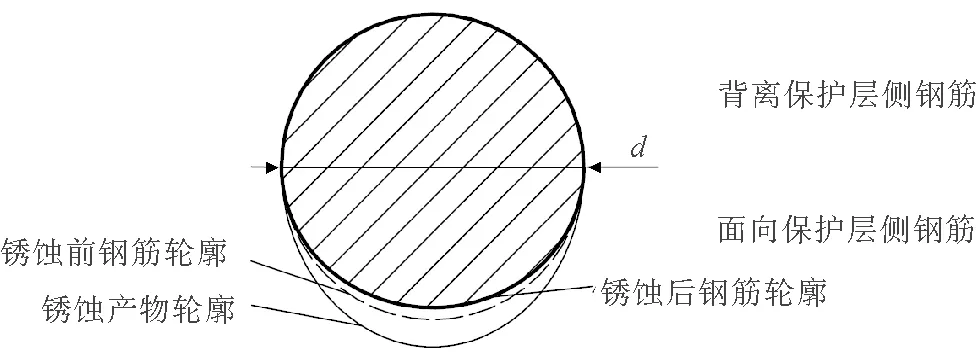
图2 钢筋非均匀锈蚀形态

1.3.2 非均匀锈蚀锈胀力分布模型

钢筋锈蚀体积膨胀必将产生作用于混凝土的锈胀力。对于非均匀锈胀力的分布已有很多研究，刘荣桂等[14]假定锈胀力为椭圆形分布并分解为均匀锈胀力与偏差锈胀力叠加计算。赵羽习等[15]提出3种非均匀锈胀压力用于反映不同的锈蚀情况。在本研究中取半圆筒状混凝土保护层，锈胀压力作用于面向保护层一侧钢筋与混凝土的接触面上，根据保护层的平衡条件取均布荷载代替其他部分混凝土对保护层的约束作用。为简化计算将保护层沿横向展开为矩形板，锈胀压力假定按正弦函数形态分布于展开的保护层表面。锈蚀产生的锈胀力如图3所示。

图3 非均匀锈胀力简化模型

建立空间直角坐标系(图4)，作用于保护层上表面的锈胀力分布取：

图4 展开板计算坐标系

(3)

其中，展开宽度a=π(c+d)/2，c为保护层厚度，d为钢筋直径。

取展开前保护层进行受力分析，根据保护层部分的受力平衡条件计算q′0与最大锈胀力q0的关系：

(4)

(5)

1.3.3 锈蚀膨胀力-应力关系

在锈胀力计算部分已考虑其他部分混凝土对保护层的约束作用，并将约束转化为力的形式。故可将展开的保护层视为两边简支的弹性板，其表面受到垂直于板面的锈胀力作用。由于钢筋纵向长度远大于钢筋直径及混凝土的保护层厚度，故弹性板纵向可假设为无限长。计算简图如图5所示。

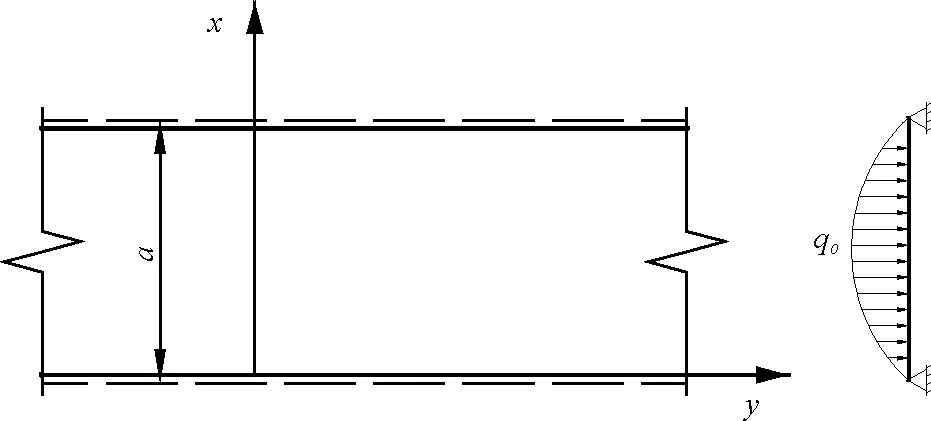
图5 展开板约束及荷载分布

由于不考虑锈胀力沿纵长方向的不均匀性，则荷载沿y方向不发生变化，即荷载函数q0=q(x)只是关于x的函数。此时弹性板的挠度函数ω(x)也仅与x有关，所以挠度函数对y的各阶导数均为0，因此弹性板的控制方程为

(6)

(7)

式中：D为弹性板的抗弯刚度；E为杨氏模量；μ为泊松比。

考虑边界条件，在x=0，a边界上：

(8)

对式(6)进行积分，得

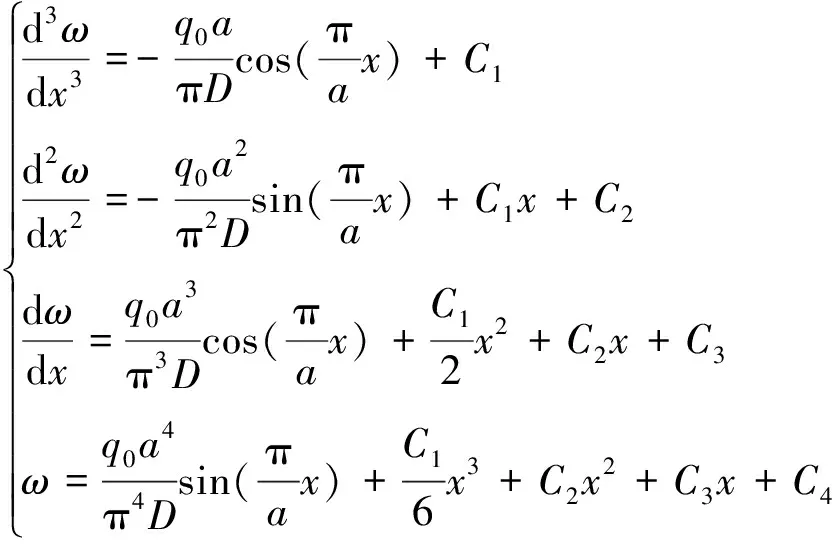
(9)

由式(8)板的边界条件，得

x=0时，(ω)x=0=0，得C4=0；

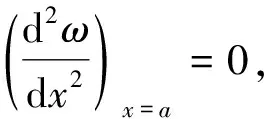
x=a时，(ω)x=a=0，得C3=0。

于是按照两边简支的无限长弹性板理论计算得到挠度函数：

(10)

不考虑泊松比μ的影响，则锈胀力函数(式(3))产生的应力为

(11)

计算由q′0产生的应力：

(12)

则在弹性板中的总应力：

(13)

(14)

(15)

在式(15)中，当σx,max=fct时，混凝土表层会因钢筋锈蚀膨胀而开裂，且裂纹开展方向平行于钢筋纵长方向，其中fct为混凝土抗拉强度。此时q0为

(16)

1.3.4 锈蚀率-变形关系

基于1.3.1章节对锈蚀模型做出的假设，取最大锈蚀深度为δ2，则在横断面上发生锈蚀的钢筋面积为

(17)

此时的名义锈蚀率为

(18)

由于钢筋锈蚀产物体积膨胀，其锈蚀产物的增长量即在横截面上面积的变化量S2为

(19)

根据前期的荷载分布假设模型，由钢筋锈蚀膨胀边界与混凝土保护层展开板内边界的变形协调条件，将锈蚀产物面积增量按照总量不变的原则，以正弦分布的方式分散到展开面上，则将引起混凝土保护层的变形。根据模型假设，产生的变形发生在坐标系z方向上且沿y轴不发生变化，于是弹性板的挠度可假设为

(20)

结合式(19)可求出待定系数A，进而求出锈蚀产物膨胀产生的挠曲线方程：

(21)

(22)

(23)

1.3.5 开裂时锈蚀深度计算

由锈胀力引起的挠度方程(式(10))与锈胀产物体积变化引起的挠度方程(式(23))，根据挠度函数的唯一性，可得锈蚀膨胀力与钢筋最大锈蚀深度的关系：

(24)

由混凝土开裂时的锈胀力(式(16))与锈胀力与最大锈蚀深度关系(式(24))可得混凝土开裂时钢筋的最大锈蚀深度：

(25)

将混凝土开裂时的最大锈蚀深度(式(24))代入名义锈蚀率(式(18))可得由已知量表示的混凝土保护层开裂时的名义锈蚀率：

(26)

1.4 保护层开裂阶段δ3计算

混凝土保护层一旦锈蚀开裂，上述弹性平板模型将不再适用。由于开裂后的混凝土保护层在中部断开，此时要考虑其他部分混凝土对保护层的约束作用，可将开裂后的保护层展开板视为两端底部简支跨中分离的两部分，并将其他部分混凝土对保护层的约束视为弹簧支座。同时考虑铁锈对裂缝的填充，为简化计算，由于铁锈对裂缝的填充量较小，故可先不考虑铁锈对裂缝的填充估算保护层外表面开裂宽度l′，再通过扣除填充部分的铁锈对l′进行修正得到裂缝宽度l。在图6中阴影部分的面积应等于锈蚀产物的增长量，开裂后由变形条件可得保护层中点的竖向位移ω2：

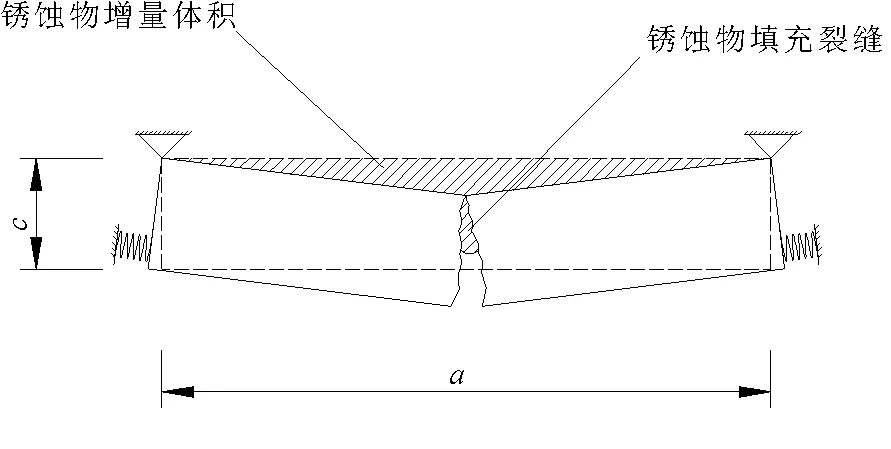
图6 保护层开裂后计算模型

(27)

通过几何关系可得保护层表面修正前裂缝宽度l′：

(28)

将式(27)代入式(28)，由于锈蚀引起的位移量很小，故式(28)可化简为

(29)

考虑铁锈对裂缝的填充对式(29)进行修正求得修正后的裂缝宽度l：

(30)

式中：λ为铁锈对裂缝的填充率。

移项得出最大锈蚀深度与混凝土表面裂缝之间的关系式：

(31)

由于锈蚀层依然按照半椭圆假设，故锈蚀率与锈蚀深度之间的换算公式式(18)在此时依然适用。

2 试验验证

2.1 锈蚀开裂时的裂缝宽度

保护层在恰好开裂时刻，钢筋的锈蚀率与恰好开裂前相同，即δ2=δ3，但开裂前后的模型假设不同。可根据开裂前的锈胀模型计算开裂时刻的名义锈蚀率，再根据此时间点的锈蚀率不变的原则，将名义锈蚀率代入锈蚀开裂后的模型，计算恰好开裂时混凝土保护层外表面的裂缝宽度。现取钢筋直径d=(18±5) mm，保护层厚度c=(40±5) mm，锈蚀膨胀率n=3±1，混凝土抗拉强度标准值fck=(2.0±0.5) MPa，混凝土弹性模量E=(30±2) GPa。将以上参数代入式(25)、式(26)估算开裂时的最大锈蚀深度及名义锈蚀率：

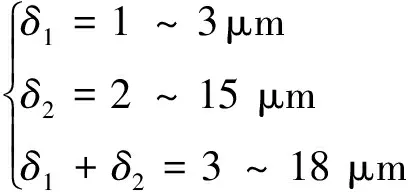
(32)

结合式(25)与式(30)可推算锈蚀开裂时刻的混凝土保护层外表面裂缝宽度：

(33)

l=3～8 μm

(34)

通过上述检验可以看到初始开裂时刻的最大锈蚀深度在3～18 μm。这与文献[16]的试验结果(保护层开裂时钢筋锈蚀深度一般为10～20 μm)基本一致。保护层外侧初始裂缝宽度在3～8 μm，由于开裂时刻的裂缝宽度较小，可观测裂缝的最小宽度一般在50～100 μm，因此在试验中很难及时观察到，且已有的研究表明保护层裂缝只有发展到一定的宽度后才会对混凝土结构的耐久性及钢筋与混凝土间的黏结力产生不利影响。因此本文将模型验证重点置于不均匀锈蚀开裂后的保护层外表面裂缝宽度与钢筋锈蚀程度的关系上。

2.2 开裂后的裂缝宽度

开裂后钢筋锈蚀深度为δmax=δ1+δ3，采用文献[17]数据对模型进行检验。该试验通过全浸泡通电加速锈蚀的方法研究了保护层厚度、钢筋直径、混凝土强度对锈蚀开裂的影响。试验结果发现锈胀产生的裂缝均产生在平行于钢筋方向，这与本模型的计算结果相一致。由于该试验是在全浸泡环境下进行的，且试验中观测到裂缝处有锈蚀产物渗出，故需考虑保护层开裂后部分锈蚀产物的溶出。铁锈溶出率取15%，锈蚀膨胀率n=2.0，铁锈裂缝填充率λ=1.0。

对试验中每种情况的3个试件裂缝宽度及锈蚀率结果取平均值，并根据锈蚀率按式(18)反推钢筋的锈蚀深度。试验及模型计算结果见表1及图7。

表1 保护层裂缝宽度与钢筋锈蚀深度

从图7可以看出公式推导结果与试验数据基本一致，两者的相关系数为0.90，非均匀锈蚀模型可以在一定程度上对锈蚀开裂状况做出预测。但是对于锈蚀深度较大的钢筋预测值偏低，分析原因主要是锈蚀程度增大，产生的锈蚀物填满裂缝后将产生更多的溶出，消散部分锈胀力，而预测模型未考虑铁锈溶出率的变化。其次铁锈在裂缝的填充过程中也将对裂缝路径边缘的混凝土孔隙进行填充，由于实际情况下裂缝路径复杂，该部分锈蚀填充量难以计算。

3 结论

1) 在非均匀锈蚀模型中应用传统的锈蚀三阶段理论，使用不同的模型对不同锈蚀阶段的钢筋进行计算，使分析明确，结果可靠。

2) 采用弹性板理论，通过非均匀锈蚀模型对锈蚀第2阶段与第3阶段的交接点，即保护层开裂时刻的钢筋锈蚀深度及保护层表面裂缝宽度进行估算，并与试验结果对比，发现该计算模型可以较准确地估计混凝土开裂时刻的锈蚀深度，也发现此时保护层裂缝宽度较小，在试验中很难加以观测。

3) 对第3阶段的锈蚀开裂状况进行计算，建立非均匀锈蚀条件下的钢筋锈蚀最大深度与保护层外表面裂缝宽度之间的关系。通过试验数据对计算结果进行验证，发现该非均匀锈蚀模型与试验结果较为符合，但对于高锈蚀程度钢筋锈蚀深度预测偏低，有待进一步研究。