2021 年高考“空间位置关系”问题聚焦

■杨 立 刘大鸣(特级教师)

2021 年高考对立体几何的考查主要是围绕“空间问题平面化,模型化和代数化”展开的。下面以2021 年高考题为载体,探究“空间位置关系”问题求解的思维方法,希望对同学们的学习有所启示。

聚焦1：“平行移动线段法”求异面直线所成的角

例1 (2021年高考全国卷)如图1,在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为( )。

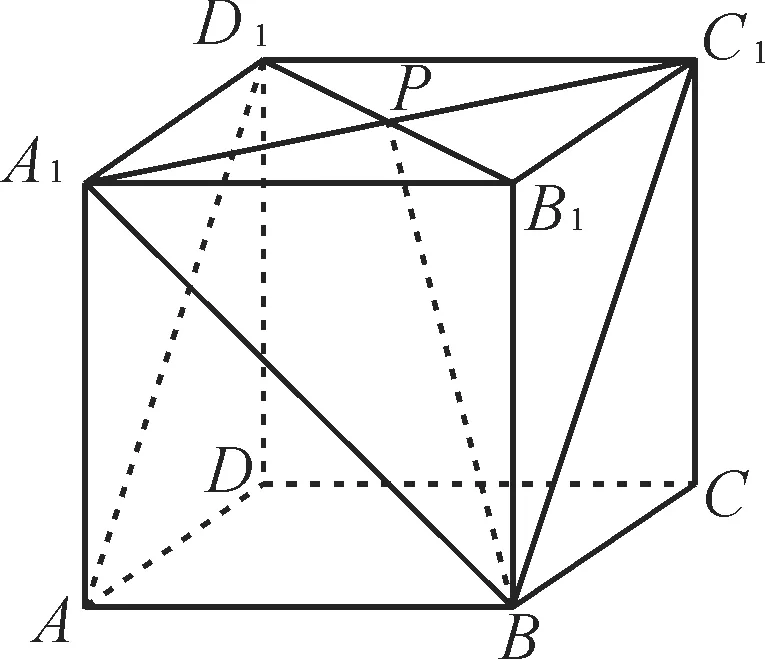
图1

聚焦2：几何法证明空间中的“垂直或平行关系”

例2 (2021 年高考全国卷)如图2 所示,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM。

图2

(1)证明:平面PAM⊥平面PBD。

(2)若PD=DC=1,求四棱锥P-ABCD的体积。

解：(1)寻找线面垂直,再利用判定定理证明面面垂直。

因为PD⊥底面ABCD,AM⊂平面ABCD,所以PD⊥AM。因为PB⊥AM,PB∩PD=P,所以AM⊥平面PBD。又因为AM⊂平面PAM,所以平面PAM⊥平面PBD。

(2)通过解三角形,求出矩形的另一边,然后求出体积。

回味：证明线线垂直的常用方法:两条直线所成的角为90°;等腰三角形三线合一;勾股定理的逆定理;菱形对角线互相垂直;线面垂直的定义及性质定理。证明线面垂直的常用方法:线面垂直的判定定理;面面垂直的性质定理;两平行线中的一条与平面垂直,则另一条也与这个平面垂直;一条直线垂直于两平行平面中的一个,则与另一个也垂直。证明线线平行的方法:三角形中位线法;平行四边形法;公理4;线面平行的性质定理;面面平行的性质定理;线面垂直的性质定理。判断线面平行的方法:线面平行的定义;线面平行的判定定理;面面平行的性质定理。

聚焦3：几何法求二面角的平面角

例3 (2021年新高考卷)如图3,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点。

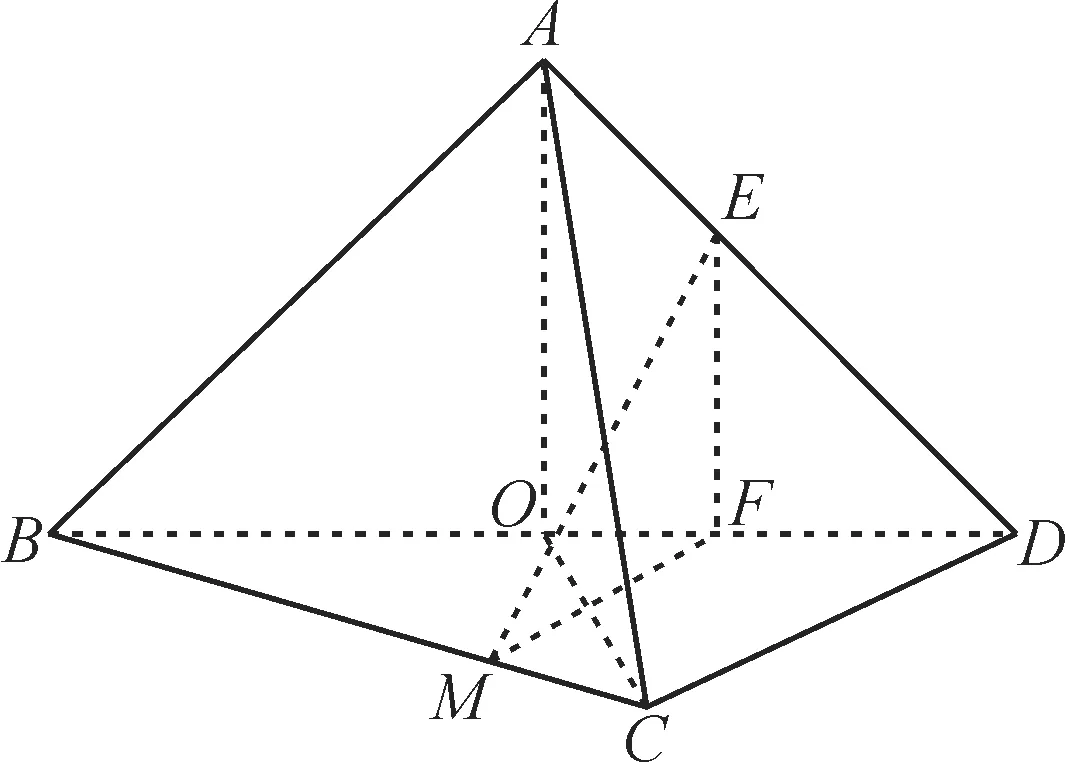
图3

(1)证明:AO⊥CD。

(2)若△OCD是边长为1 的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积。

解：(1)由AB=AD,O为BD中点,可得AO⊥BD。因为平面ABD⊥平面BCD,所以AO⊥平面BCD。又CD⊂平面BCD,所以AO⊥CD。

(2)作EF⊥BD于点F,作FM⊥BC于点M,则EF//AO。

回味：利用定义法求作二面角的平面角,要合理选择棱上的点,且过这点在两个平面内分别引棱的垂线,这两条射线所成的角,就是二面角的平面角。

若PB的中点为M,BC的中点为N,求AC与MN夹角的余弦值。

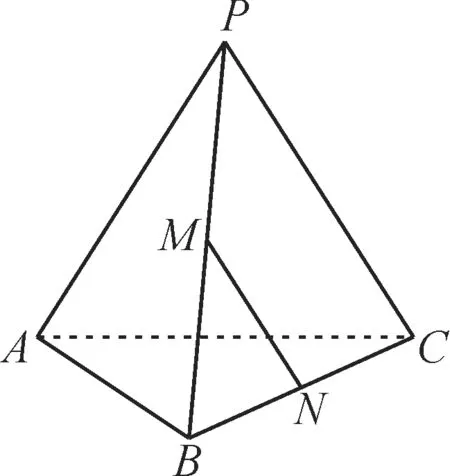
图4