空间几何体求解中的“思维误区”

■杨 汉

在空间几何体的学习中,由于同学们缺少“空间问题平面化,模型化和代数化”的意识,解题时容易出现思维误区,下面结合实例剖析之。

误区1：三棱锥的体积求解中忽视“等积变换”

例1 如图1,在棱长为5 的正方体ABCD-A1B1C1D1中,EF是棱AB上的一条线段,且EF=2,Q是A1D1的中点,点P是棱C1D1上的动点,则四面体PQEF的体积( )。

图1

A.是变量,且有最大值

B.是变量,且有最小值

C.是变量,且有最大值和最小值

D.是一个不变量

错解：应选A 或B或C。

剖析：上述解法错选的原因是:忽视了三棱锥体积求解中的“合理变换底面和高”。

由AB⊥侧面AA1D1D,可知QA为点Q到AB的距离。

由EF=2,可知S△QEF为定值。

由C1D1//AB,结合线面平行的判定定理得C1D1//面QEF,则C1D1到面QEF的距离为定值。而P是棱C1D1上的动点,所以点P到平面QEF的距离也为定值。

由上可知,四面体PQEF的底面积和高均为定值,则四面体PQEF的体积为定值。应选D。

警示：求三棱锥的体积问题,可任选一面作为底面,目标是易求出该底面的面积和对应的高。

误区2：不善于将空间问题转化为平面问题,缺少割补法的意识

例2 如图2,一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D,E,F,且知SD∶DA=SE∶EB=CF∶FS=2∶1,若仍用这个容器盛水,则最多可盛原来水的( )。

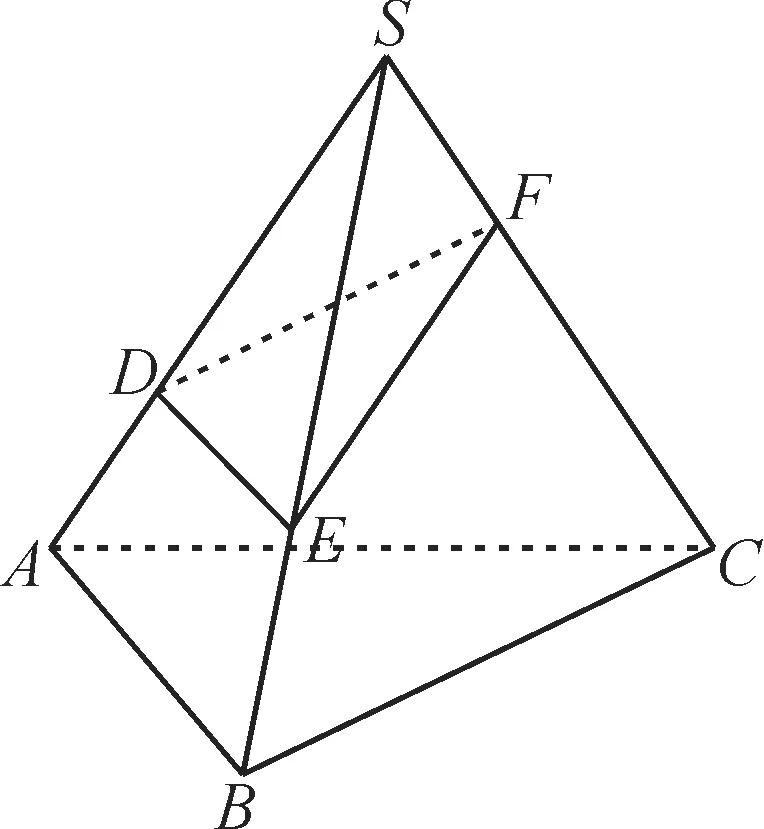
图2

当平面EFD与水平地面平行时,容器盛水最多。

由SD∶DA=SE∶EB=CF∶FS=2∶1,可设F,C在平面SAB上的射影分别为G,H,则FG∶CH=SF∶SC=1∶3。

警示：理解这个容器盛水最多的意义,再结合三角形的相似比是解答本题的关键。

误区3：忽视题设或定理中的条件

例3 设a,b为两条直线,α,β为两个平面,且a⊄α,a⊄β,则下列结论中不成立的是( )。

A.若b⊂β,a//b,则a//β

B.若a⊥β,α⊥β,则a//α

C.若a⊥b,b⊥α,则a//α

D.若α⊥β,a⊥β,b//a,则b//α

错解：应选A。

剖析：上述解法错选的原因是:不能准确把握条件a⊄α,a⊄β,忽视了空间中平行、垂直关系的判定定理的条件。

对于A,由b⊂β,a//b,且已知a⊄β,根据线面平行的判定定理得a//β,A 正确。对于B,由a⊥β,α⊥β,根据线面位置关系得a⊂α或a//α,而已知a⊄α,所以a//α,B 正确。对于C,由a⊥b,b⊥α,可得a⊂α或a//α,而已知a⊄α,所以a//α,C正确。对于D,由a⊥β,b//a,可得b⊥β,因为α⊥β,所以b⊂α或b//α,即不能得到b//α,D 错误。应选D。

警示：利用直线与平面平行或垂直,平面与平面平行或垂直的判定定理时,一定要注意定理成立的条件。

误区4：两直线位置关系判断中忽视“反证法”的应用

例4 已知m,n为异面直线,m⊂平面α,n⊂平面β,α∩β=l,则直线l( )。

A.与m,n都相交

B.与m,n中至少一条相交

C.与m,n都不相交

D.至多与m,n中的一条相交

错解：应选A。

剖析：忽视题设条件,缺少反证法研究问题的意识。

假设直线l与m,n都不相交,因为m⊂平面α,n⊂平面β,所以m//l,n//l,所以m//n//l。这与m,n为异面直线矛盾,则假设错误,所以直线l与m,n中至少一条相交。应选B。

警示：简单的空间位置关系的判断,可根据题设条件,结合反证法容易得到答案。

误区5：线线、线面、面面平行关系转化不当

例5 如图3所示,平面α//平面β,AC与BD为异面直线,且AC⊂α,BD⊂β,M,N分别为AB,CD的中点,求证MN//平面β。

图3

错解：由α//β,AC⊂α,可得AC//β。由BD⊂β,可得AC//BD。

因为M,N分别为AB,CD的中点,所以MN//BD。又MN⊄β,BD⊂β,所以MN//平面β。剖析：上述解法认为两个平行平面内的两条直线必平行,忽视了异面的情形。

由AB∩AC=A,可得AB,AC确定一个平面γ,则γ∩α=AC。

由B∈AB,AB⊂γ,B∈β,可得B是γ与β的公共点,于是可设β∩γ=BE。取CE的中点P。由α//β,α∩γ=AC,β∩γ=BE,可得AC//BE。

由M,P分别为AB,CE的中点,可得MP//BE。因为BE⊂β,MP⊄β,所以MP//平面β。

在△CED中,P,N分别为CE,CD的中点,可得PN//DE。

因为PN⊄β,DE⊂β,所以PN//β。

又因为MP∩PN=P,所以平面MNP//平面β。

因为MN⊂平面MNP,所以MN//平面β。

警示：在证明线面平行时,一定要强调直线不在平面内,否则会出现错误。在解决线面、面面平行时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”。