“三法”化解表面积与体积问题

■孙建国

空间几何体中的有关表面积与体积问题是高考的一个热点。这类问题,常用的解题方法有三种,即公式法,构造法,参数法。下面就空间几何体中的有关表面积与体积问题进行举例分析,供同学们学习与参考。

一、公式法

例1 如果有一个正四棱柱,它的体积是16,它的高是4,它的八个顶点都在一个球面上,那么这个球的表面积为_____。

二、构造法(或补形法)

例2 如图1所示,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,边AB的中点是E,现将△ADE与△BEC分别沿虚线ED与EC向上折起,使得A、B两点都与点P重合,那么三棱锥P-DCE的外接球的体积是( )。

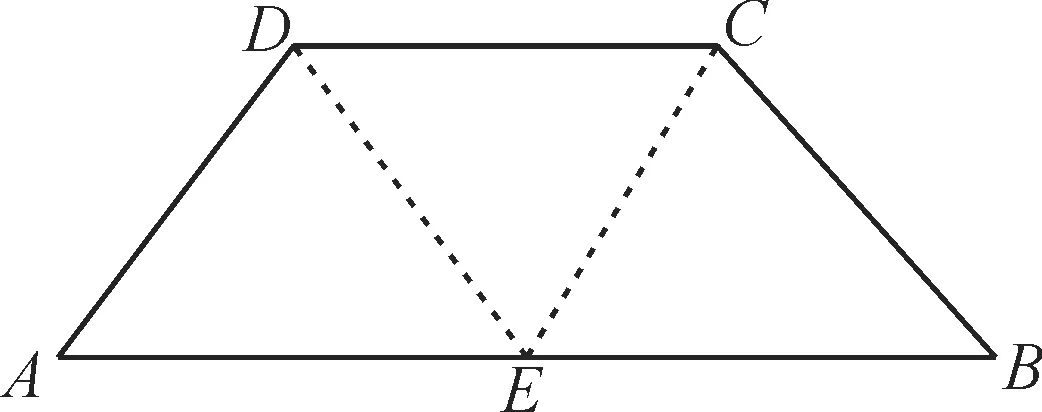
图1

评析：解题时,将正四面体构造成正方体,就容易求出外接球的体积了。

三、参数法

评析：所谓参数法,其实就是方程与函数思想在这类问题中的应用。