基于FWA-DBN的航空发电机偏心故障诊断
杨占刚, 徐海义, 成博源, 石旭东
(中国民航大学电子信息与自动化学院, 天津 300300)
0 引 言
航空发电机作为航空电源系统的主电源,为各机载用电设备提供能源,保障着电源系统的稳定运行。航空发电机故障会严重影响整个飞机系统的安全性,其早期故障主要分为以定、转子绕组短路为代表的电气故障与以转子偏心为代表的机械故障。据统计,偏心故障在凸极式同步发电机总故障中占比近40%,偏心故障包含静态偏心与动态偏心:静态偏心主要由定子铁芯形变与轴承定位不良导致,动态偏心主要由轴承疲劳、不平衡磁拉力、机械共振以及转子过热等导致。偏心故障会造成发电机气隙磁场不对称,进而导致三相感应电动势(electromotive force, EMF)、负载电流不平衡,影响飞机电网的电能质量,并且不平衡磁拉力将加深偏心程度,造成更严重危害。为此,需要对航空发电机早期微小偏心故障进行在线监测,避免航空发电机故障可能造成的重大安全事故。
目前针对发电机转子偏心故障诊断方法的核心思想是对易于测量的电磁特征(气隙磁密、电磁力波、反EMF、定子电流等)与机械特征(振动噪声)进行时频域分析。根据气隙磁密、电磁力波等参数的空间阶次与时间频率谐波次数变化的不同,可实现偏心类型的识别,但无法准确判断偏心的程度。定子空载反EMF与定子电流在偏心后将出现三相幅值不平衡,同时增加转频谐波,当每相绕组支路数大于1时,将导致单一支路的故障幅值差异在并联支路结构下被抵消,三相输出波形故障变化不易识别。此外,在相同偏心程度下,不同负载特性与容量对故障后产生的谐波幅值也存在影响,同样使得频域特征不易区分。为了提高传统时频域分析方法故障特征提取与诊断的准确性,许多研究将传统特征提取方法与智能诊断算法相结合。文献[10]利用小波包分解(wavelet packet, WP)提取故障电压频率特征,通过长短时记忆(long short term memory, LSTM)网络诊断偏心转子马达故障。文献[11]利用集成经验模态分解(ensemble empirical mode decomposition, EEMD)提取偏心转子振动信号特征,通过支持向量机准确诊断电机偏心故障。但由于WP、EEMD等信号分析方法易出现频率混叠与高频分量丢失问题,导致此类方法在多并联支路绕组的偏心同步发电机故障频率特征提取时效果不佳。目前在电机、变压器、齿轮箱、传感器等故障诊断中多采用深度学习方法,典型算法为深度置信网络(deep belief network,DBN)。DBN算法可实现航空发动机、发电机短路故障诊断,其改进算法被应用于飞机旋转整流器故障、滚动轴承故障诊断。DBN网络结构一般由经验定义,其层数或节点数过多会造成训练时间过长,相反则会造成训练精度不足与特征丢失,因此有必要优化DBN结构以提升特征提取与诊断效率。
基于此,本文针对具有多并联支路绕组结构的航空发电机偏心故障,搭建发电机模型与负载场路耦合模型进行仿真。针对DBN结构中各隐藏层节点数选取问题,采用烟花算法(fireworks algorithm,FWA)建立最优DBN,对航空发电机偏心故障进行特征提取与诊断。
1 发电机偏心故障建模
如图1所示,在静态偏心下,转轴旋转中心为,即转轴几何中心,空间各处气隙大小不随旋转变化;在动态偏心下,转轴旋转中心为,非转轴几何中心,空间各处气隙大小随旋转变化。
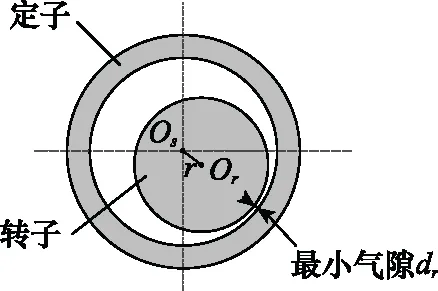
图1 转子偏心结构图Fig.1 Rotor eccentric structure diagram
定义发电机转子偏心度为
=
(1)
式中:为转子中心与定子中心的距离;为凸极发电机正常最小气隙长度。
建立航空发电机有限元仿真模型,主要参数如表1所示。
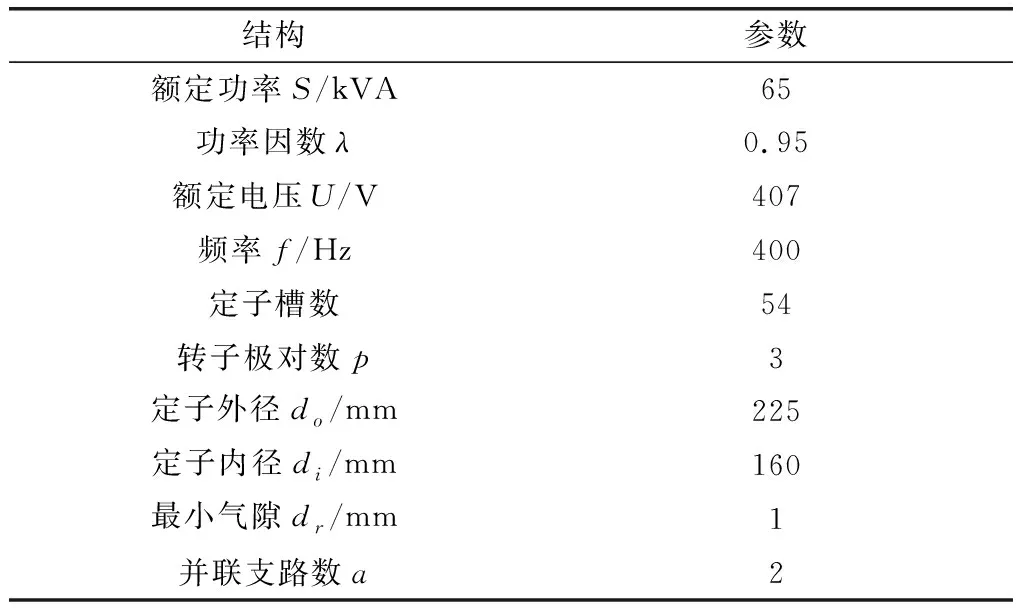
表1 同步发电机主要参数
2 发电机偏心故障分析
2.1 空载分析
定子各槽导体空载反EMF解析表达式为
()=()
(2)
式中:为每槽导体匝数;为导体有效长度;为定子内圈半径;()为第槽处径向气隙磁密。
无偏心时,气隙磁密沿圆周径向等幅分布,各槽内导体EMF叠加得到的三相空载反EMF幅值相等。静态偏心时气隙磁密分布仅与偏心方向有关,不随转子旋转变化,三相绕组各支路的反EMF波形如图2所示。
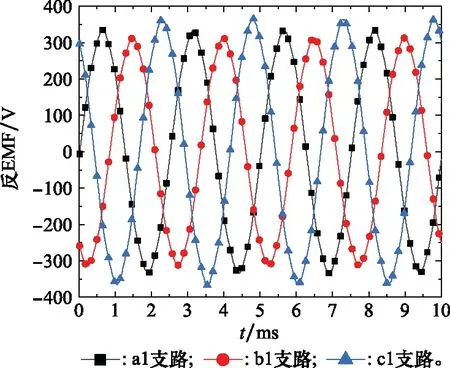
图2 静偏心绕组支路反EMFFig.2 Back EMF of winding branches under static eccentricity
动态偏心时气隙磁密分布随转子旋转呈周期性变化,各支路反EMF在静态偏心的基础上还增加了周期性下凹特征,波形如图3所示。
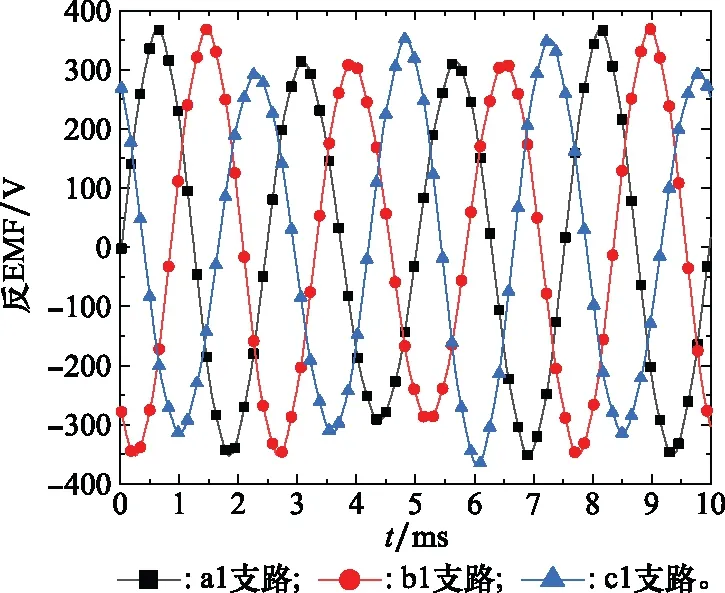
图3 动偏心绕组支路反EMFFig.3 Back EMF of winding branches under dynamic eccentricity
由于每相绕组的两条支路在空间上分别处于靠近偏心位置处与远离偏心位置处,每条支路上的反EMF波形变化不同。经并联绕组结构对各支路反EMF叠加输出,各支路反EMF的不平衡将被抵消。图4以A相绕组为例,当发生动态偏心时, A相并联输出端反电动势幅值在多个电周期内没有明显波动。
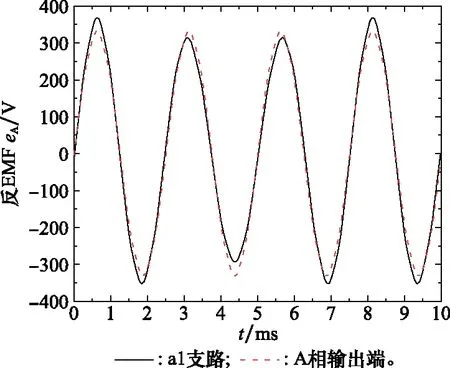
图4 反EMF对比Fig.4 Comparison of back EMF
图5中对比了动态偏心分别为025、05、075与静态偏心分别为025、05、075时的A相并联输出空载反EMF波形与局部放大波形。根据波形对比,不同偏心故障对输出波形影响均较小。
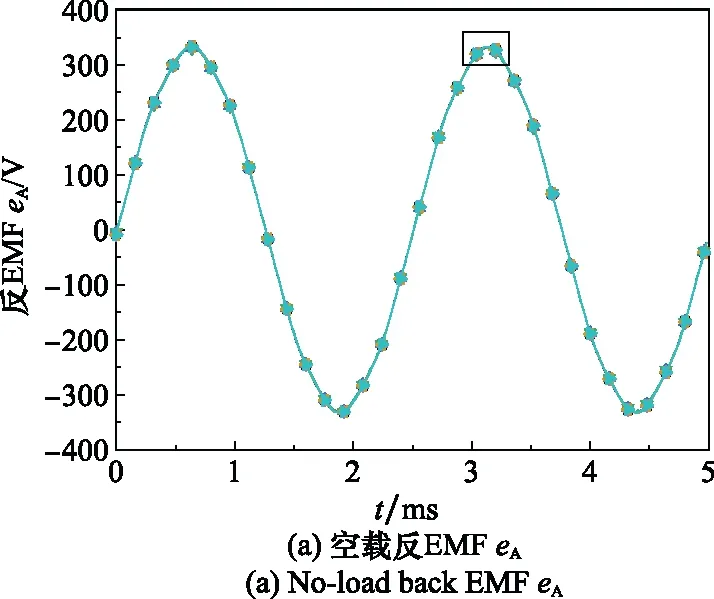
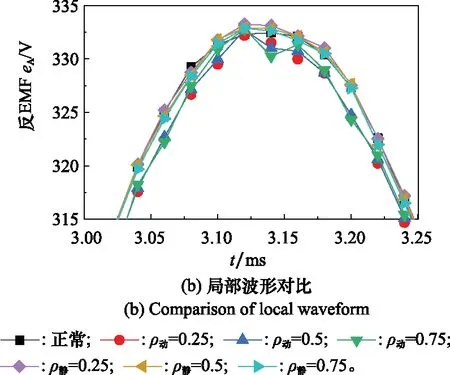
图5 不同偏心故障A相空载反EMFFig.5 No-load back EMF eA under different eccentricity
当励磁电流=186 A,无偏心三相空载反EMF幅值约为33246 V。表2中对比了不同偏心故障前后的三相空载反EMF幅值,可见不同类型与不同偏心程度造成幅值差异较小,且故障幅值与故障程度不呈线性关系。
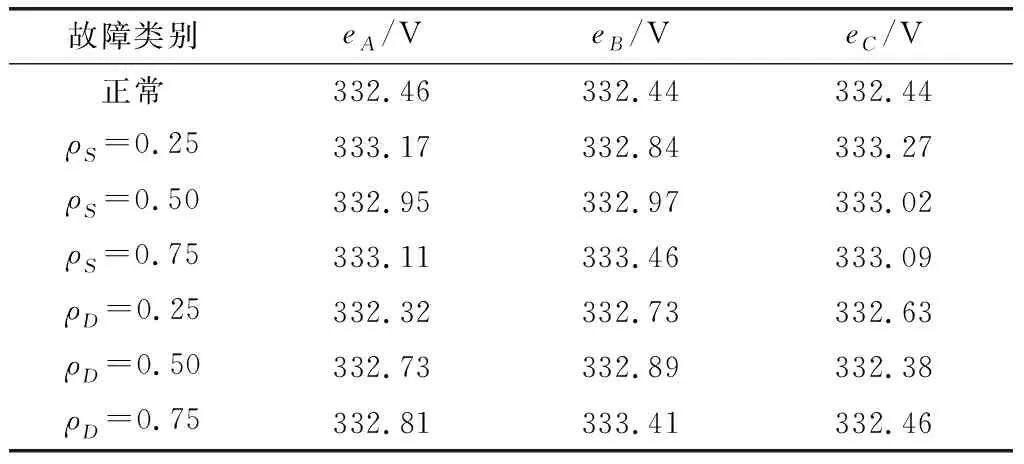
表2 三相反EMF幅值对比
并联支路绕组对三相不平衡度的抵消作用使得空载反EMF故障变化较小且无明显规律,这对区分发电机偏心类型与偏心程度造成困难。
2.2 额定负载分析
搭建发电机额定负载场路耦合外电路,负载为纯阻性,如图6所示。其中定子三相绕组每条支路电感=0112 mH,电阻=0126 Ω,负载阻值=275 Ω。
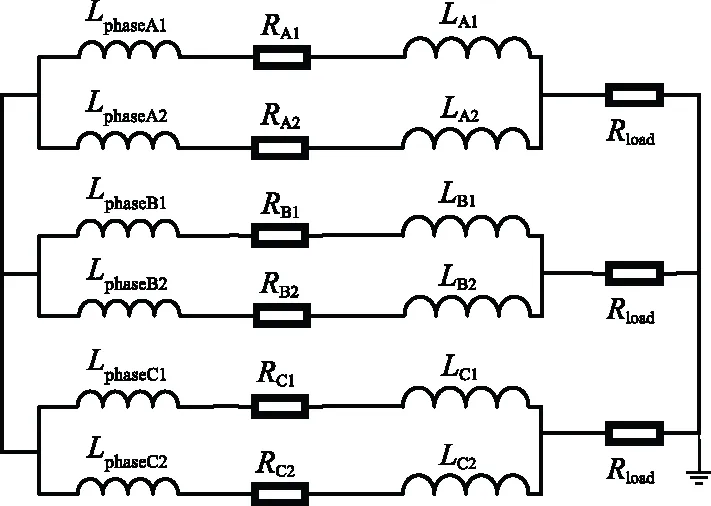
图6 场路耦合外电路Fig.6 Field-circuit coupling circuit
当发电机带负载运行时,输出电压谐波主要包含由凸极转子绕组磁场、电枢电抗等引入的奇数次谐波以及故障后产生的分数次转频谐波和负载感应谐波,这将使得三相输出波形变化相对明显。不同偏心故障时定子A相输出电压变化如图7和图8所示。偏心故障时单支路绕组电流波形也存在不平衡现象,不同偏心故障造成的支路电流波形变化规律与反EMF波形变化一致,并联叠加后的输出电流不平衡度下降。图9和图10分别为静态偏心=075下定子支路电流、输出端电流波形。
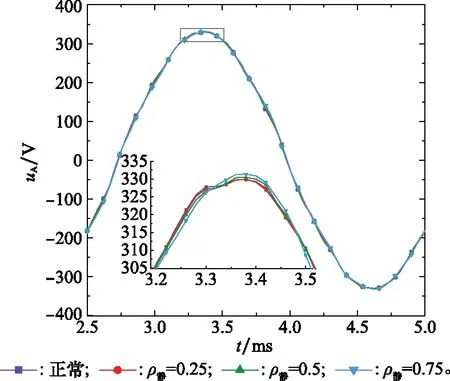
图7 不同静偏心程度下A相输出电压uAFig.7 Output uA under different static ρ
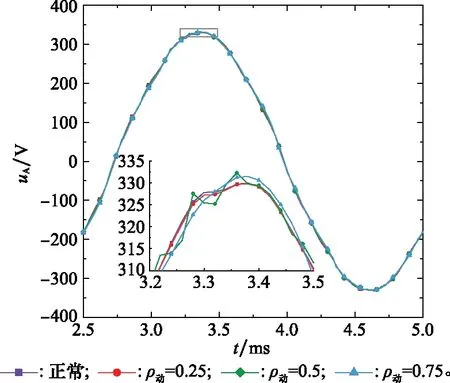
图8 不同动偏心程度下A相输出电压uAFig.8 Output uA under different dynamic ρ
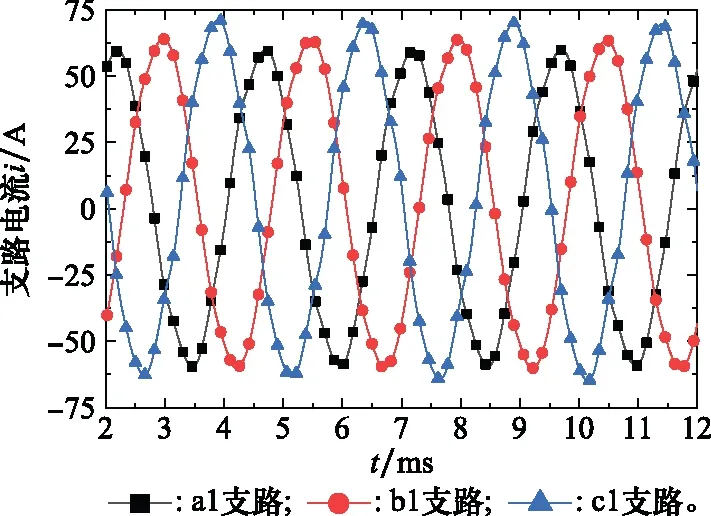
图9 静偏心绕组支路电流Fig.9 Current of winding branches under static eccentricity

图10 静偏心输出电流Fig.10 Output current under static eccentricity
表3为额定负载运行时发电机发生不同偏心故障前后输出电压、电流最大幅值,由幅值变化可知静态偏心与动态偏心造成输出幅值变化规律不同。静态偏心下,当故障程度=025时,三相输出最大幅值略小于正常幅值,当故障程度较大时,三相输出最大幅值大于正常幅值,且三相间幅值不同。当故障程度加深时,输出幅值有增大趋势。动态偏心下,当故障程度=025时,三相输出最大幅值同样略小于正常幅值,但当故障程度较大时,三相输出最大幅值变化较大,且没有明显变化趋势规律。可见,较小程度的偏心故障对发电机输出几乎没有影响,但是当偏心程度持续增大时,将对飞机电网电能质量有较大影响。恒励磁负载运行下,发电机偏心故障输出特征差异相较于空载运行时更易区分。
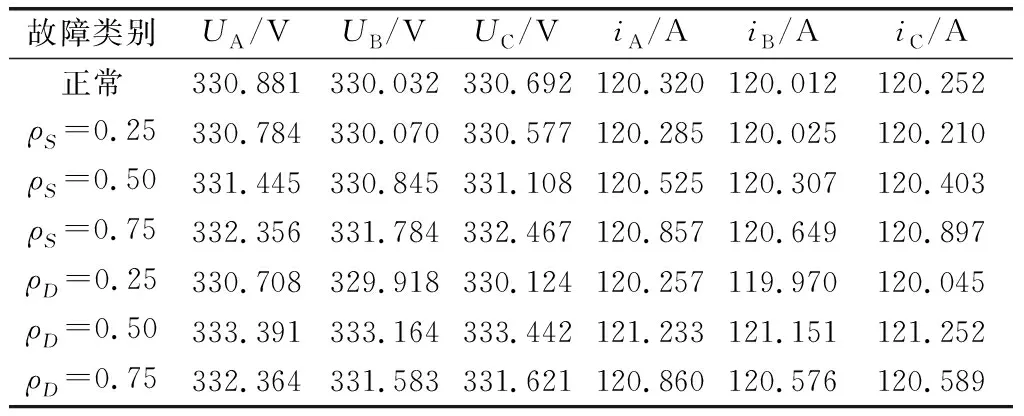
表3 三相幅值对比
当发电机不同负载容量运行时,发生不同类型与程度偏心故障的时域输出变化差异不同,造成故障不易识别。因此,可以借助深度学习算法挖掘不易区分的故障特征,实现不同运行工况时偏心故障诊断。
3 偏心故障特征提取与诊断算法
3.1 DBN算法
DBN由多个受限玻尔兹曼机(restricted Boltzmann machine,RBM)叠加构成,在预训练阶段逐步提取输入数据的原始特征信息,并以输出均方根误差最小化为目标进行反向微调,模型结构如图11所示。
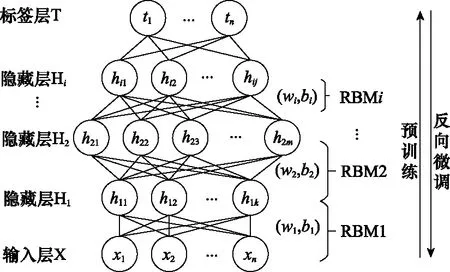
图11 DBN结构Fig.11 DBN structure diagram
单个RBM是由可视层和隐藏层组成的概率生成模型,仅不同层间神经元通过权值向量和偏置向量、连接,结构如图12所示。
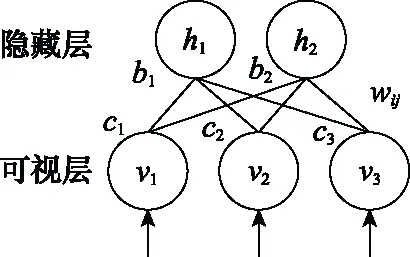
图12 RBM结构Fig.12 Structure of RBM
可视层神经元和隐藏层神经元间的能量函数定义为
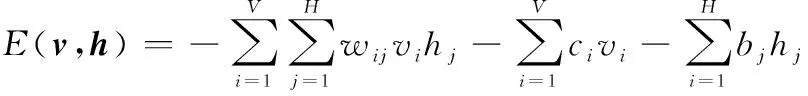
(3)
式中:和分别为两层神经元的输入与输出状态;为各层神经元间权值;和分别为两层的偏置;和为神经元数量。由式(3)可得两层间联合概率分布为
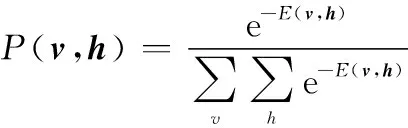
(4)
根据对比散度算法计算可视层与隐藏层各神经元状态,隐藏层向量和可视层向量的条件概率分布可用激活概率表示,代表数据正向训练过程与数据反向重构过程,分别为
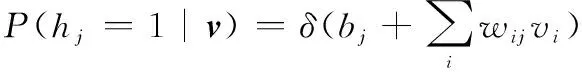
(5)
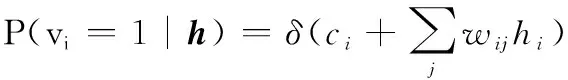
(6)
式中:激活函数采用非线性Sigmoid函数,表达式为
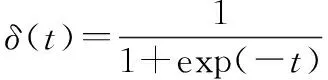
(7)
将负对数似然函数作为训练过程中的目标函数如下:
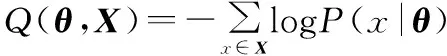
(8)
式中:(={,,};为训练数据。
为达到重构数据期望误差最小化,根据梯度下降法将目标函数对参数迭代求导,训练得到的参数可最大程度保留原始数据特征。
在DBN结构[X-H-H-…H-T]的输出标签层T前采用极限学习机ELM作为分类器,ELM结构为[H-1-H-T]。H-1层输出的故障特征即ELM输入,ELM随机设定权重与偏置向量计算得到隐藏层H,并根据最小二乘解确定训练输出,快速完成故障特征与诊断标签间的转化。
选择合适的RBM数量与神经元数可提升DBN网络的训练速度与特征提取准确性,因此可利用FWA优化确定最适合于航空发电机偏心故障数据的DBN网络结构。
3.2 FWA
FWA属于群体智能优化算法,由烟花爆炸产生火花现象启发得到,算法通过控制每个烟花爆炸半径和子火花数量,搜索更优的目标。
爆炸半径和爆炸子火花数目可以定义为

(9)
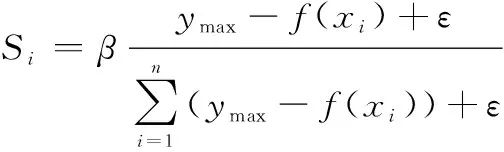
(10)
式中:和为爆炸半径和子火花数目的预设最大值控制因子;、为烟花种群适应度极值;()为误差适应度函数;为烟花数量;为极小的非零常数。
爆炸通过位置偏移在维搜索空间内产生新的子火花,新爆炸子火花生成公式如下:
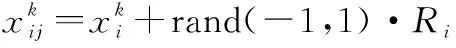
(11)
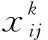
随机选取一个子火花进行多样性高斯变异,生成高斯变异子火花如下:
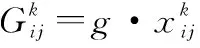
(12)
式中:表示服从N(1, 1)分布的随机数。
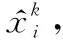
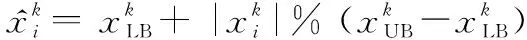
(13)
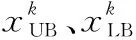
适应度最优的烟花将被选择为下一代烟花,剩余烟花采用轮盘赌策略择优保留并传递给下一代。每个烟花个体被选择的概率()如下:
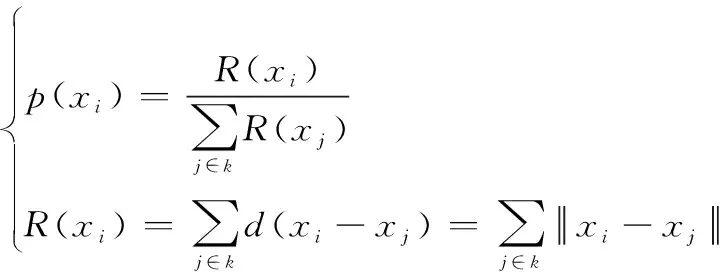
(14)
式中:(·)为当前个体与其他个体的距离之和。
综上,基于FWA-DBN的航空发电机偏心故障特征提取与诊断流程如图13所示。
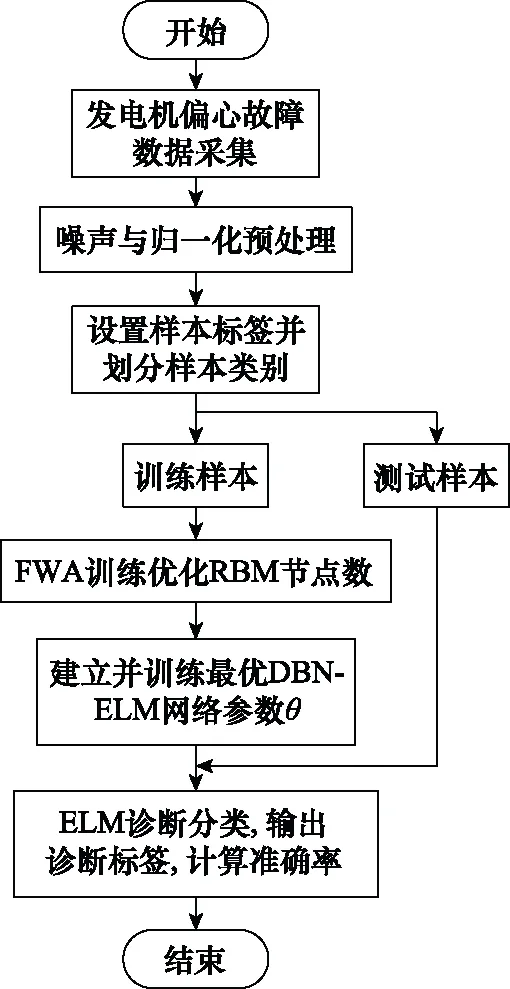
图13 基于FWA-DBN的航空发电机偏心诊断流程Fig.13 Aviation generator eccentricity diagnosis diagram based on FWA-DBN
3.3 数据采集与诊断
诊断类别共7种,包括正常状态、3种程度动态偏心故障与3种程度静态偏心故障,仿真采集航空发电机三相空载反EMF、额定负载输出三相电压与电流原始数据。设置采样频率为50 kHz,单次采样时间0.1 s,将同种故障模式下的9个时域数据样本混合为1组,共45 000个样本点,每种故障模式采集30组数据,共采集210组,构成210×45 000原始数据集。考虑到实际采样中的信号干扰,将原始数据经噪声破坏与归一化预处理后,在每种类别的30组故障数据中选择25组故障数据作为训练样本,由FWA根据175组发电机故障数据训练得到最优DBN诊断模型参数,对其余35组测试数据进行诊断,对比样本真实故障情况,计算诊断准确率。
FWA适应度函数取样本训练输出误差函数,适应度函数如下:
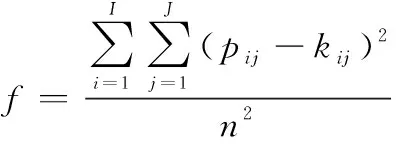
(15)
式中:为RBM层数;为隐藏层神经元个数;为烟花与子火花总数目;为样本期望输出值;为样本实际值。
利用FWA训练确定每个隐藏层的最佳神经元数量,FWA初始参数设定如表4所示。

表4 FWA参数
深度学习网络多采用三层隐藏层叠加结构,可使数据重构误差较小,本文DBN模型同样选用三层RBM与ELM组合结构[X-H-H-H-H-T],设置每层RBM迭代计算20次。训练过程中选用不同FWA初始动量与学习率,并根据所有烟花与子火花平均适应度进行多次迭代寻优,适应度曲线如图14所示。由适应度曲线可知,随着迭代次数增加与烟花种群更新,训练误差逐渐下降。当第一层神经元数量较多时,初始误差较小,曲线收敛较快,反之亦成立;当第三层神经元数较少时,最终收敛误差较大,反之亦成立。
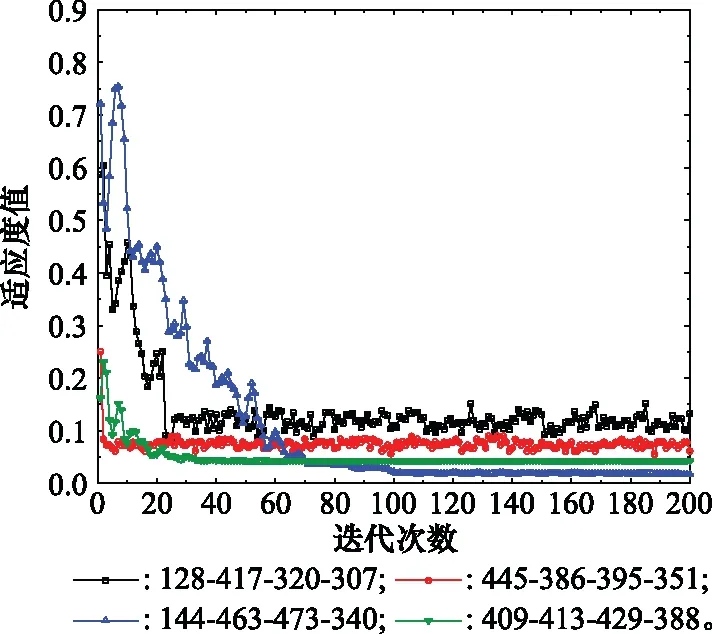
图14 参数寻优适应度Fig.14 Parameter optimization fitness
最终确定各隐藏层神经元数量为[144-463-473-340],最佳适应度达9994%。根据此结构建立最优DBN-ELM网络模型,并对训练集与测试集样本进行诊断。
单次诊断结果如图15所示,纵轴为7种故障类别编号,编号1代表发电机正常运行,编号2-4代表发电机3种程度动态偏心故障,编号5-7代表发电机3种程度静态偏心故障。单次训练样本准确率达到97714%,单次测试样本诊断准确率达到97.143%。
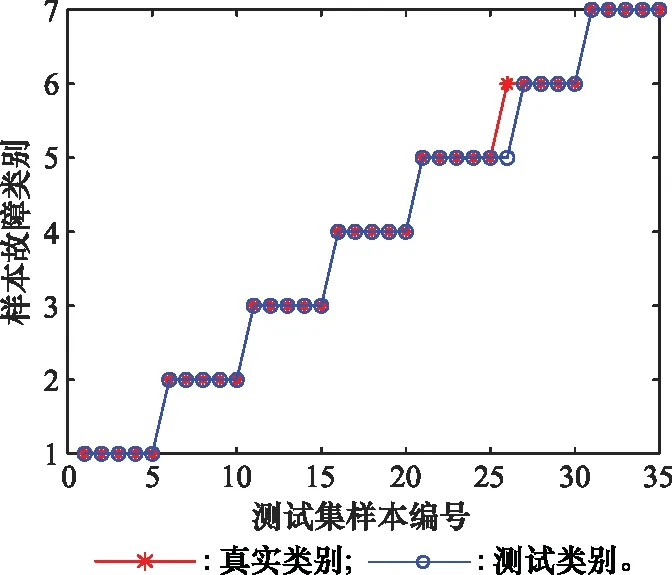
图15 测试集故障诊断结果Fig.15 Fault diagnosis results of testing set
为表明采用FWA优化算法确定RBM神经元数的优势,表5对比了不同RBM神经元数下模型20次平均诊断准确率与训练时长,对比结构均为4层RBM,各层均迭代20次。
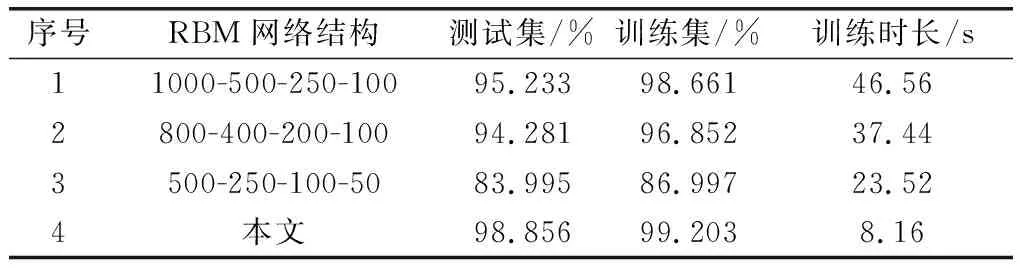
表5 不同RBM网络结构对比
第一组对比结构准确率较高,但是由于神经元数最多,训练时间也较长;第二组对比结构神经元数相比第一组略有减少,准确率有所下降;第三组对比结构神经元数较少,提高了训练速度,但是损失了训练准确率。可见较多的神经元数能够提升训练与诊断准确率,但会消耗训练时长。FWA能够提升DBN特征提取性能,从而保证DBN-ELM网络诊断准确率与训练速度。
3.4 其他算法对比
为了进一步验证FWA-DBN算法的故障诊断效果,采用不同诊断算法进行对比。
(1) FFT+FWA-DBN:利用快速傅里叶变换(fast Fourier transform, FFT)对故障前后三相电压、电流数据进行初步特征提取,将前20次谐波幅值特征用于训练与诊断,网络结构不变。
(2) SDAE+SVM:利用堆叠降噪自动编码器(stacked denoised autoencoder, SDAE)对原始故障数据实现快速特征提取与数据降维,设置网络隐含层神经元数为[150-75-20],稀疏系数为0.15,惩罚项权重为3,并使用支持向量机(support vector machine,SVM)进行故障分类。
(3) LSTM+Softmax:利用LSTM提取原始故障数据中的有效特征,设置网络隐含层神经元数为[150-75-20],学习率为0.01,使用Softmax层对故障样本进行精确故障诊断。表6为3种对比方法诊断结果平均准确率与训练诊断时长。
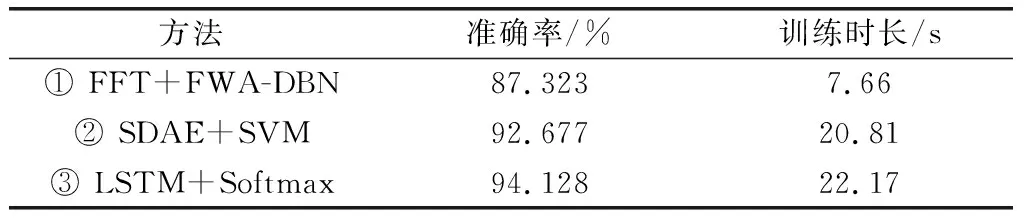
表6 3种方法的诊断准确率
分析表6可知,采用不同算法的诊断结果有明显差异:方法①与本文方法的不同点在于对训练数据预先进行了信号处理,由于采用FFT仅提取故障的主要次数谐波特征,训练数据较少,训练时长较短,但是存在部分频域特征丢失的问题,造成诊断准确率较低;方法②和方法③都与本文方法类似,同样对原始故障数据进行训练,能够避免方法①中人工特征提取的弊端,准确率更高,但是模型结构参数或分类器参数都由经验定义,容易出现局部最优或过拟合,训练时长也远大于本文方法。因此,本文FWA-DBN方法在航空发电机偏心故障诊断方面明显优于其他方法。
4 结 论
本文提出一种基于FWA-DBN的故障诊断方法,实现对航空发电机空载与额定负载运行工况进行偏心故障诊断。本方法根据发电机故障输出数据,利用群体优化算法训练得到最佳DBN结构,能够解决多并联支路绕组结构与较小偏心程度带来的诊断困难问题,更快速且准确地提取难以区分的故障特征,提高了航空发电机偏心故障诊断效率。本改进算法适用于实际航空发电机故障检测,能够提供最优训练与诊断模型。

