基于分布式深度学习的边缘服务放置策略
邹 虹, 白陈阳, 何 鹏,*, 崔亚平, 王汝言, 吴大鹏
(1. 重庆邮电大学通信与信息工程学院, 重庆 400065; 2. 重庆高校市级光通信与网络重点实验室,重庆 400065; 3. 泛在感知与互联重庆市重点实验室, 重庆 400065)
0 引 言
随着5G网络的快速部署,增强现实(augment reality, AR)、虚拟现实(virtual reality, VR)等新型应用场景不断涌现,这些应用往往具有低时延和大带宽的需求,给计算、存储能力不足且电量受限的移动设备带来了极大的挑战。根据思科的预测,2023年5G用户将达到14亿,平均5G连接速度将达到575 Mb/s。2013年欧洲电信标准组织(European Telecommunications Standards Institute, ETSI)提出移动边缘计算(mobile edge computing, MEC),通过在无线接入网侧部署基站和边缘服务器,从而为这些应用需求提供支持。如何为移动设备提供低时延的持续服务是制约移动边缘计算网络持续发展的瓶颈之一。
在移动边缘计算网络中,由于边缘服务器的通信、计算、缓存等资源受限,且用户需求多样性、区域热点差异性等问题的存在,导致边缘计算服务器负载不均衡,从而使接入到高负载边缘服务器的用户服务质量大大下降,边缘服务放置技术则是解决这一问题的关键技术之一。合理的边缘服务放置能够保证用户的服务质量要求,并且平衡部分高负载服务器的工作负担。如何根据用户服务质量要求以及资源限制等信息进行合理的边缘服务放置成为移动边缘计算网络服务放置中亟待解决的关键问题之一。由于应用服务提供商(application service provider, ASP)的成本限制及服务能力有限,只能在边缘服务器中部署部分热点服务,因此在实际进行边缘服务放置时,需要考虑用户当前接入的边缘云是否具有其请求的服务。将服务放置到某一个边缘云后,需要进一步为放置的服务分配计算、存储等资源,从而支持服务的正常运行并保证持续高质量的用户服务。
关于移动边缘计算的服务放置问题,国内外研究人员已开展研究。文献[6]根据ETSI模型设计了一种新的MEC服务放置方案,建立了整数线性规划问题,提出了一种禁忌搜索算法,在满足计算资源、延迟要求和服务可用性的约束条件下有效平衡了计算负载,但禁忌搜索算法的缺点可能使其陷入局部最优。文献[7]提出了一种动态服务放置策略,该策略在考虑平均服务放置延迟和成本的情况下最大化ASP的利益。所提算法根据延迟和成本等参数的阈值进行迭代,并重新进行服务放置,在一定程度上减少了延迟,但时间复杂度过高。文献[8]考虑了长期成本约束下的多用户服务放置场景,建立了长期成本约束条件下平均时延最小化问题,并提出了集中式的Markov近似策略和分布式的最佳响应更新策略,解决了单节点覆盖的用户服务请求决策问题,实现了次优解。文献[9]考虑了ASP预算约束下的服务放置,以时隙为单位,在所有边缘服务器中租用部分资源进行服务放置,利用组合上下文多臂赌博方法进行边缘服务放置决策,有效降低了服务时延。文献[8-9]仅考虑了资源限制,但是未考虑资源分配问题。当服务被放置到某一边缘云后,需要进一步为服务分配合理的资源从而支持服务的正常运行。文献[10]考虑了边缘节点可用计算资源有限情况下车载无线通信技术(vehicle to everything, V2X)的服务放置,为了解决核心网与边缘计算混合环境中的最佳V2X服务放置问题,提出了一种低复杂度的贪婪算法解决方案,达到了接近最优的性能。文献[6-10]主要考虑了单一类型的服务放置,以及针对多边缘节点的服务迁移,但均未考虑服务异构性问题,在实际服务放置过程中,服务类型往往是多样化的,对单一类型的服务进行优化无法满足实际场景的需求。文献[11]考虑了边缘计算系统节点特征和用户位置的异构性问题,在每个边缘节点中放置多种类的服务,以最大化服务放置奖励为优化目标,提出了一种近似算法,但未考虑服务放置成本以及资源分配问题。
针对以上现存问题,本文从用户的服务质量要求等实际情况出发,提出了一种基于分布式深度学习的边缘服务放置策略。考虑到用户服务请求类别的多样性及ASP的服务放置成本,对边缘服务放置策略与移动边缘计算网络的计算-存储资源进行了联合优化。为克服用户服务请求发送至ASP远端云服务器的响应时间过长,严重降低用户服务体验等问题,通过在靠近用户侧的边缘云部署一定数量的热点应用服务,从而快速响应用户的服务需求,提高用户的服务质量。其次,考虑到移动边缘计算网络的计算-存储资源有限,为降低用户服务请求的响应时间及ASP的服务部署成本,设计了最小化所有用户服务请求的时延与加权服务放置成本总和的优化目标,将优化问题建模为混合整数非线性规划问题。为求解所设计的优化目标问题,首先使用凸优化理论求解出了给定服务放置策略情况下边云最优的计算资源分配方案。由于传统数值优化方法在求解最优服务放置策略时存在算法时间复杂度过高等问题,本文设计了基于分布式深度学习的边缘服务放置算法。该算法不仅降低了用户服务请求时延及ASP的服务放置成本,而且能随着时间的推移逐渐逼近全局最优的服务放置策略。
1 系统模型
MEC网络能够为电量和计算资源不足的用户设备提供分布式计算资源和低时延服务,合理的边缘服务放置策略可以提高MEC网络中的用户服务质量。由于资源受限,导致延迟敏感型任务和重流量负载型应用的服务质量降低。因此,本文在距离用户较近的网络边缘部署MEC服务器,利用MEC的计算能力处理靠近网络边缘的用户服务请求。本节首先介绍了MEC网络的异构服务网络架构,然后根据用户接入网络情况建模服务放置模型和通信模型。
1.1 网络模型
系统的网络架构如图1所示,在宏基站(macro base station, MBS)覆盖范围内存在多个小基站(small base station, SBS),SBS均带有边缘云增强,令集合={1,2,…,,…,}表示全部边缘云集合。
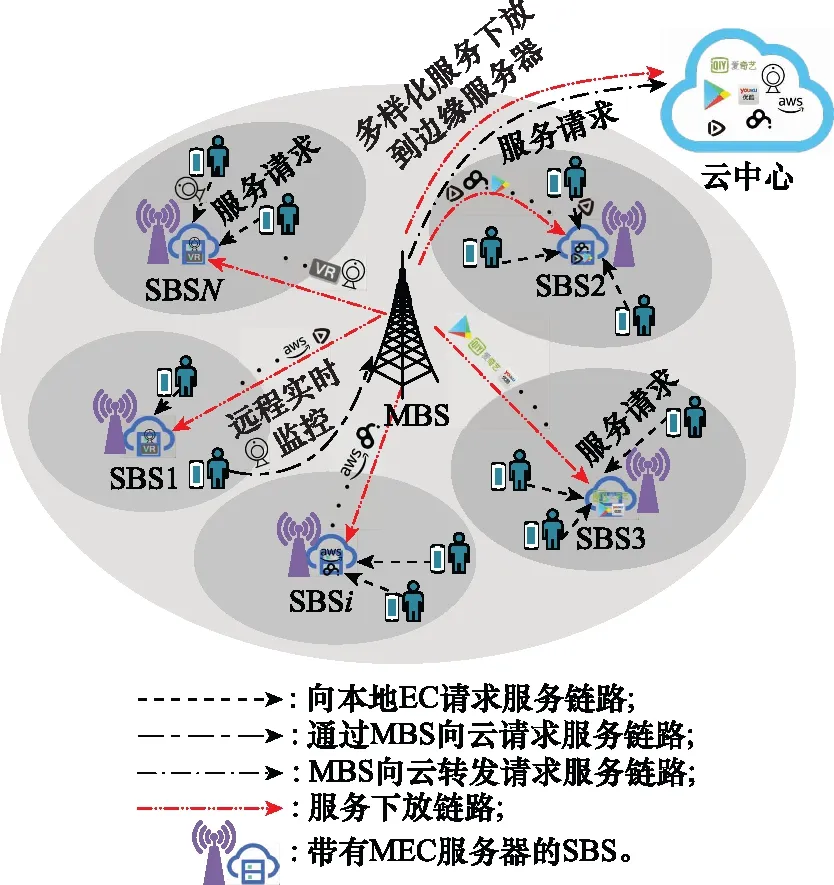
图1 网络架构Fig.1 Network architecture

1.2 服务放置模型
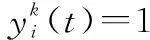

(1)
式中:表示服务所需要的存储资源;表示边缘云全部的存储资源。
1.3 无线通信模型
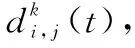
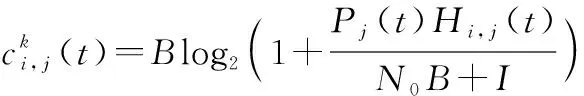
(2)
式中:是信道带宽;是加性高斯白噪声双边功率谱密度;是信道中的随机噪声。
2 问题公式化
2.1 上行传输时延模型
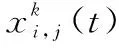

(3)
此外,本文考虑到边缘服务器的计算-存储资源有限,因此ASP在每个边缘云上只能部署有限的服务。当用户所在的边缘云没有该用户所需要的服务时,该用户只能通过所在的SBS上传自身的服务请求至拥有所有服务的云服务器。因此,用户的上行传输时延主要有两种情况:
(1) 边缘云具有第个用户所请求的第种服务。在该种情况中,边缘云所服务的第个用户的上行传输时延为

(4)
(2) 当边缘云不具有第个用户所请求的第种服务时,边缘云所服务的第个用户的服务请求只能通过边缘云上传到MBS,再通过核心网转发至云中心。因此,边缘云所服务的第个用户上行传输时延为

(5)

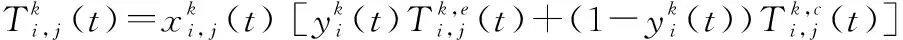
(6)
2.2 计算时延模型
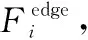
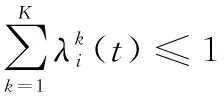
(7)
因此,边缘云所服务的第个用户的计算时延为
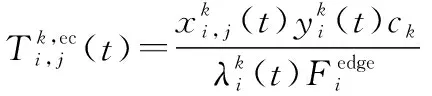
(8)
值得注意的是,当用户的服务请求不能被本地边缘云所响应时,该用户的服务请求只能通过本地的SBS上传至ASP的云服务器。令表示云服务器的计算能力,可得边缘云所服务的第个用户的服务请求被云服务器所计算的时延为
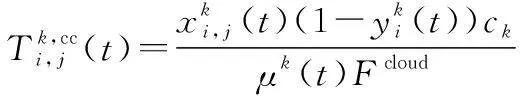
(9)
式中:()∈[0,1]表示时刻云服务器分配给第种服务的计算资源比例。云服务器分配给全部服务的计算资源比例需满足:
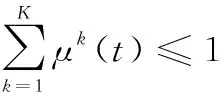
(10)
针对于云服务器存储服务的条件,本文假设ASP的云服务器具有全部类型的服务。
综上所述,边缘云所服务的第个用户的最终计算时延为
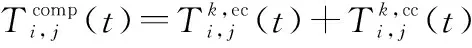
(11)
2.3 问题公式化
首先,为缓解大量服务请求上传到远端云服务器对核心网造成的流量拥塞以及解决如何进一步提高用户的服务体验等问题,部署在边缘服务器上的服务应最大化满足用户的需求。但如果每个边缘服务器都部署所有的服务将导致部署成本过高等问题。针对于该问题,本文制定了如下的优化目标:
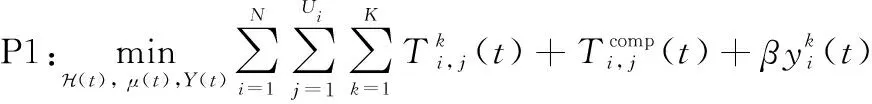
s.t. 式(1),式(3),式(7),式(10)
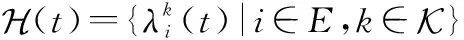
3 问题解耦
本文求解问题P1的总体思路如下。首先令时刻ASP已经作出最优的服务放置策略()。在该条件下,问题1将转化为不含整型变量的边云计算资源分配问题P2,其表述如下:
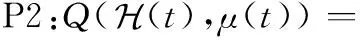
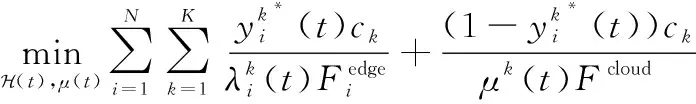
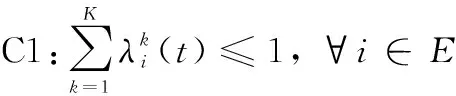
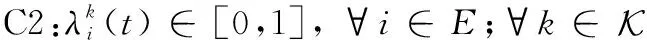
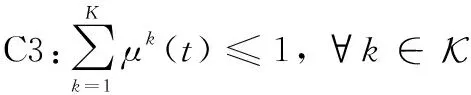
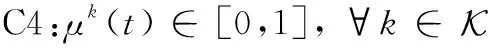
式中:C1表示边缘云分配给所托管的服务的计算资源不能大于其最大计算资源;C2表示边缘云分配给第种应用服务的计算资源比例;C3表示云服务器分配给所托管的服务的计算资源不能大于其最大计算资源;C4表示边缘云分配给第种服务的计算资源比例。
P2为凸优化问题。
为证明问题P2为凸优化问题,首先将验证目标函数和约束条件分别为凸。可以看出,约束条件C1~C4为线性约束,因此满足凸函数性质。
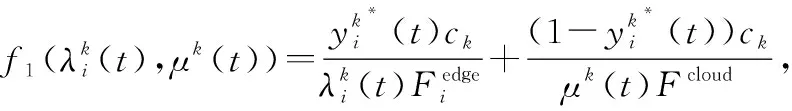

通过相关的计算,得到:
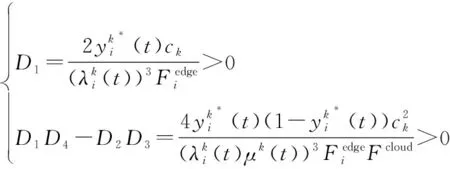
证毕
边缘云与云服务器分别分配给服务的最优计算资源比例为
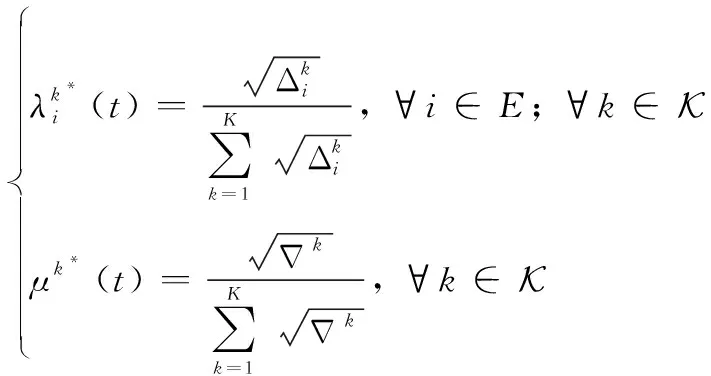
(12)
观察问题P2可以看出,优化目标的第一项只与约束条件C1与C2相关,第二项与约束条件C3与C4相关。因此,问题P2可以分解为两个子问题,分别为边缘云的计算资源分配问题P2_1与云服务器的计算资源分配问题P2_2。下面将求解子问题P2_1,并在其基础上求解问题P2_2。问题P2_1表述如下:
C1, C2
(13)
运用拉格朗日乘子法消去约束式,得优化算子为
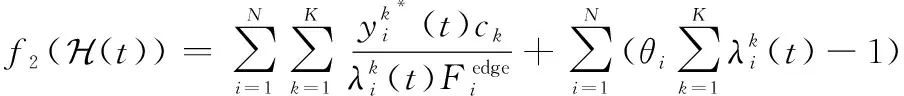

(14)
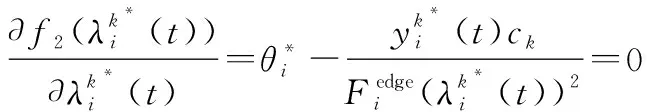
(15)
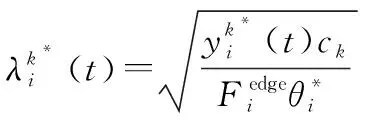

(16)
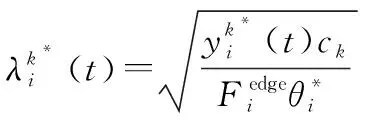
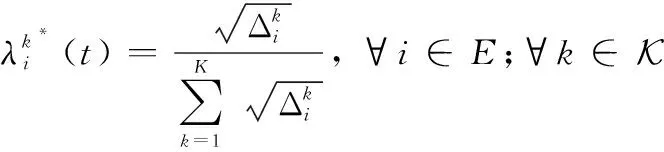
(17)
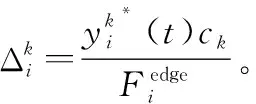
接下来将求解问题P2_2。问题P2_2表述如下:
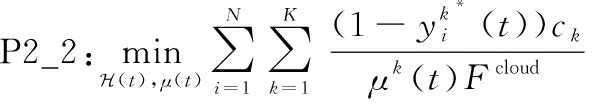
C3, C4
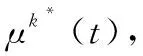
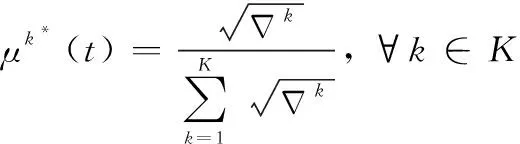
(18)
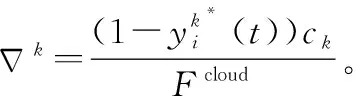
证毕
通过以上的理论推导,证明了在任意时刻,已知ASP的最优服务放置策略()条件下的最优边云计算资源分配策略。下面将求解在任意时刻,ASP最优的服务放置策略()。首先通过观察可知,问题P1是一个混合整数非线性规划问题(mixed integer nonlinear program, MINLP)。如果通过穷举法寻找最佳的服务放置策略(),所需要的计算时间随着用户、边缘云和服务请求种类的数量成指数级增长,显然不利于实际的移动边缘计算网络。因此本文的目标是设计一种时间复杂度较低且能通过学习随着时间的推移逐渐逼近最优解的解决方案。基于此,本文提出了一种基于分布式深度学习(distributed deep learning, DDL)的边缘服务放置策略。
4 基于DDL的边缘服务放置策略
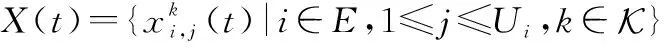
(19)
由于所求解的二进制服务放置集合()可能存在的组合数为2种,随着边缘云和服务种类数量的增加,该组合数大小将呈指数增长,导致在任意时刻寻找最优的服务放置行为()是一个NP难问题。基于此,本文使用基于深度神经网络(deep neural network, DNN)的参数化函数近似表示服务放置策略。不同于经典的深度学习方法,本文使用了基于DDL的边缘服务放置(DDL based edge service placement, DDL-ESP)策略,通过个并行的DNN获得种候选的二进制的服务放置行为。该方法不仅具有更快的收敛速度,且能获得更高的服务放置准确度。
4.1 基于DDL的边缘服务放置模型
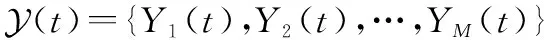
4.2 边缘服务放置动作生成
如图2所示,对于时刻的输入(),使用个DNN生成个候选的边缘服务放置行为,其中每个DNN将对应生成一个边缘服务放置行为。令第个DNN输入与输出的关系函数为(,()),可得第个DNN输出的服务放置行为:
(20)
式中:表示第个DNN内部各层神经元之间的连接权重与偏置集合。具体解释为由于DNN的各层之间的神经元通过简单的线性函数进行前向传递,其表达式如下:

(21)
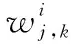
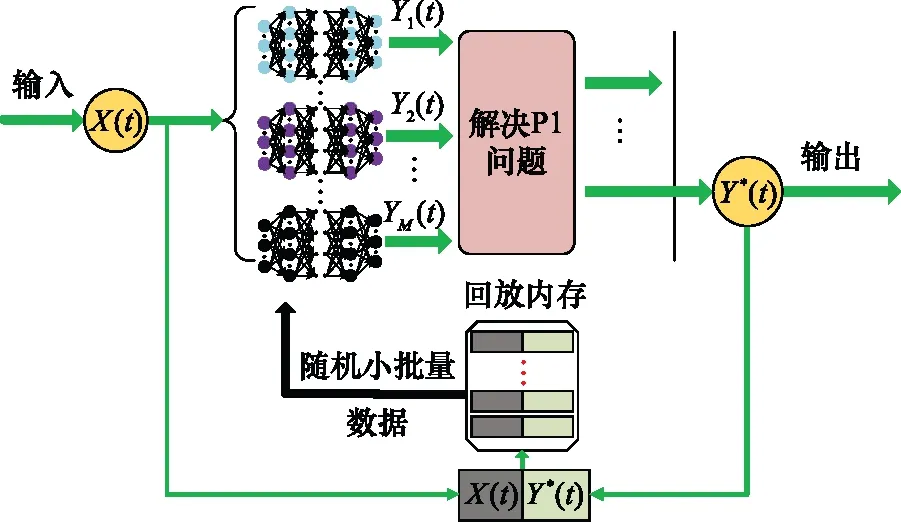
图2 DDL-ESP模型Fig.2 DDL-ESP model
通过以上对所提模型的输入与输出关系的理论推导知道,当第个DNN在任意时刻所观察的环境状态(),都可根据式(20)做出响应的服务放置行为()。基于此,问题P1转化为边云计算资源分配问题P2。前面的工作已经研究了已知边缘服务放置策略()情况下,最优的边云计算资源分配策略如式(12)所示。最后,服务放置动作生成的具体流程如图3所示。
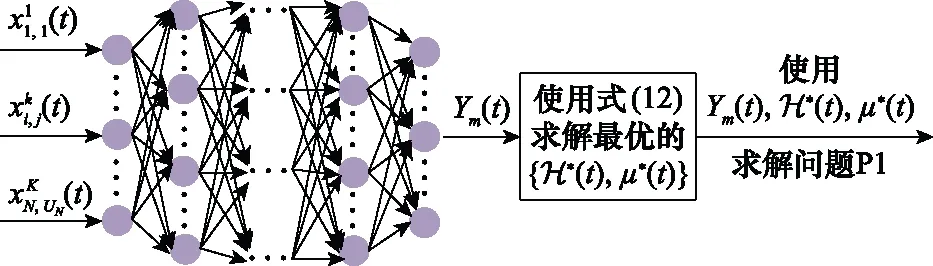
图3 服务放置动作生成过程Fig.3 Process of service placement action generation
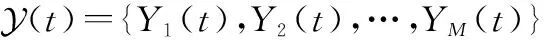
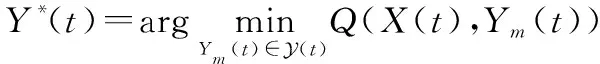
(22)
根据式(22)获得的最优服务放置行为()将作为所提服务放置策略的最终输出。
4.3 DDL在线学习过程
为了让DDL方法能够随着时间的推移渐进地学习接近全局最优解的边缘服务放置策略,本文使用了深度强化学习的经验回放机制。DDL方法完成在线学习过程如下所述:首先,在当前任意时刻,根据式(22)获取最佳边缘服务放置决策(),然后将环境状态()拼接为带有标签的数据((),())并存入有限容量的记忆回放内存。当记忆回放内存被标签数据占满,其中最为陈旧的数据条目将被记忆回放内存所丢弃。为了使个DNN能在线学习最优的边缘服务放置策略,每隔时间,从记忆回放内存为每一个DNN随机选取大小为的标签数据,用于训练DNN,从而实现在线学习最优的服务放置策略过程,其流程如图4所示。其中,每个DNN采用梯度下降算法最小化当前标签与最优标签的损失函数来优化每个DNN的参数值,其损失函数表述为
(,(),())=-()log(,())- (1-())log(1-(,()))
(23)
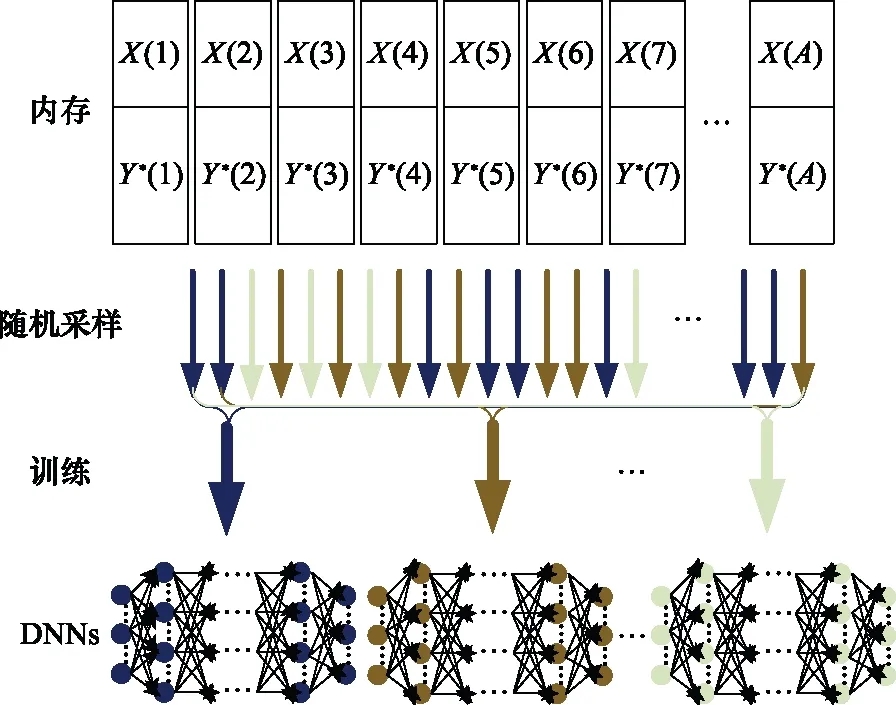
图4 DDL-ESP在线学习过程Fig.4 Online learning process of DDL-ESP
通过对基于DDL的边缘服务放置策略详细的介绍与说明,推导出了任意时刻,最优的服务放置行为()产生过程及如何在线学习渐近最优的边缘服务放置策略,最终的实现流程如算法1所示。

算法1 DDL-ESP算法输入 时刻t,用户的服务请求集合X(t)输出 时刻t,边缘云最优的服务放置行为Y*(t)1. 随机初始化每个DNN的内部参数ξm;2. for t=0,1,…,+∞ do3. 以X(t)作为每个DNN的输入,得到边缘服务放置行为集合(t);4. 使用式(22)挑选出最优的服务放置Y*(t);5. 以Y*(t)作为该环境状态X(t)的标签;6. 检查记忆回放内存是否占满,如果占满删除时间最为陈旧的标签数据,并存入该时刻最新的数据(X(t),Y*(t));7. ift>0 and t%τ==0 do8. 随机从记忆回放内存中为每一个DNN选取大小为A的数据集,使用式(23)作为损失函数,然后使用随机梯度下降算法训练每一个DNN更新内部参数ξm,从而实现在线地学习最优服务放置策略π*;9. end if10. end for
首先随机初始化个DNN的内部参数值并保证每个DNN内部参数不能完成相同。此外,还需初始化记忆回放内存为空。通过大量的仿真分析可知,当>1时,DDL-ESP算法能快速收敛到最佳的服务放置策略。
5 仿真分析
本文采用Python IDE Pycharm作为实验的仿真软件。当前Pycharm有两个版本,分别为专业版与社区版。专业版功能强大,主要是为Python和Web开发者而准备的。由于社区版具备完成仿真实验所需的全部模块(如numpy、scipy、tensorflow、keras等),所以使用版本为Pycharm Community Edition 2019.2.5的IDE进行仿真实验。与此同时,为缩短仿真时间,使用戴尔易安信PowerEdge R730机架式服务器(Xeon E5-2603 V3/8GB/1.2TB)搭建仿真平台。
在边缘计算网络中,本文假设MBS覆盖范围内存在的SBS数量=3且每个SBS覆盖的用户数=3(∈)。每个SBS分配给每个用户的上行传输带宽=10 MHz。此外,假设系统中服务请求的种类数量=4。其他仿真参数设置如表1所示。
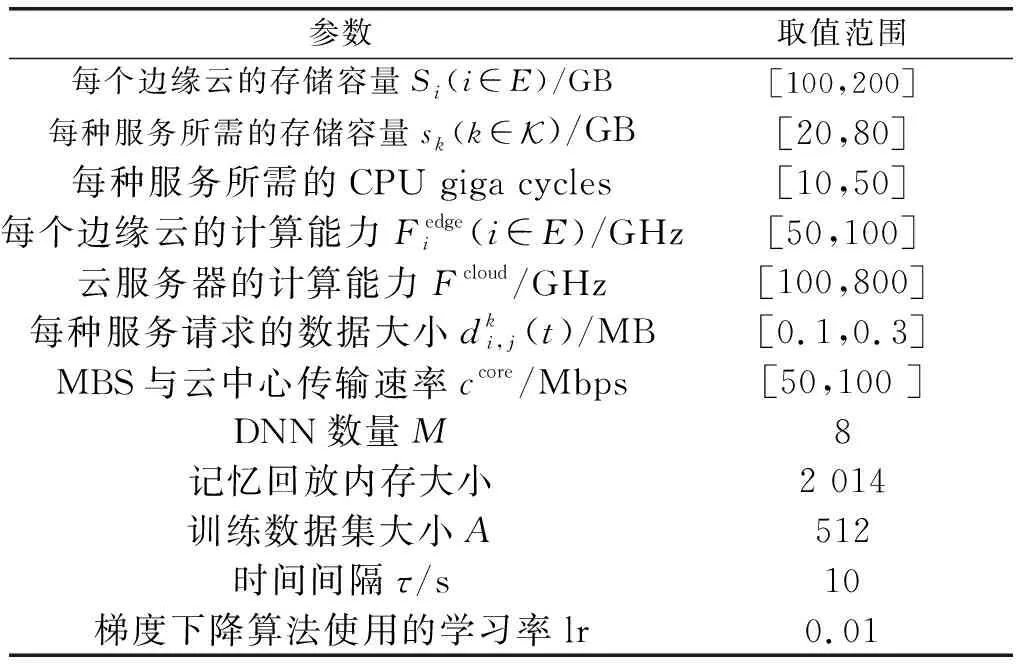
表1 仿真参数
图5仿真了在不同DNN数量情况下,DDL-ESP算法所产生的所有用户加权时延总和与穷举法所计算的全局最优的加权时延总和比值(在图中用时延增益表示)随时间推移的变化曲线。可以看出,随着时间的不断推移,当≥8时,所提出的DDL-ESP算法最终能以大约98%的时延增益逐渐逼近穷举法所产生的全局最优解。即,所提算法最终所计算出的所有用户加权时延总和与全局最优解之间的误差大约为2%。此外还可以看出,随着DNN数量的不断增大,所提算法的收敛性也不断变快。其产生的主要原因在于,随着值的增大,DDL-ESP算法在任意时刻的服务放置行为生成过程中将会产生更多的服务放置行为。即,在这些服务放置行为中,将可能出现更好的服务放置行为,使得问题P1的值更小,从而使得DDL-ESP算法在线学习过程中更容易接近全局最优的服务放置策略。但值得注意的是,增大值也意味着算法在学习过程中将需要训练更多的DNN,导致训练时间过程变长等问题。因此,在实际运用中,值的设置需要结合设备的计算能力及外部环境变化的快慢,才能使训练时间与算法收敛性达到最佳的平衡状态。
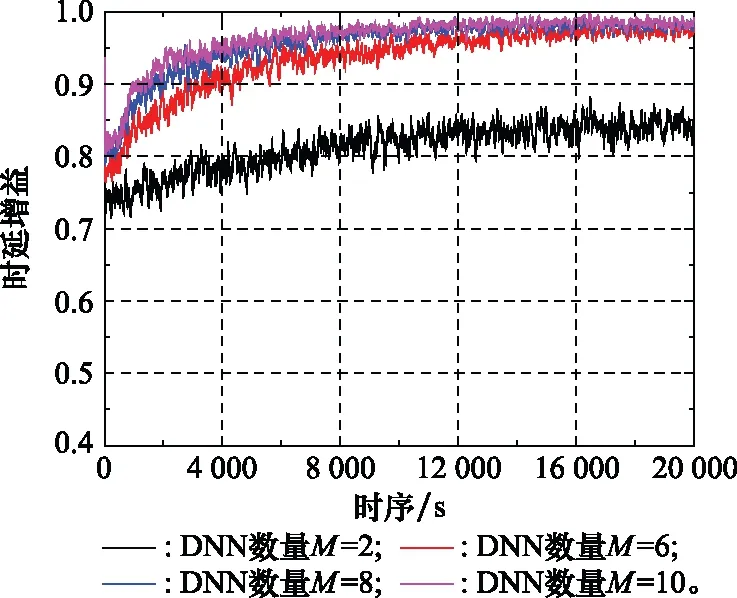
图5 DNN数量与DDL-ESP算法收敛性Fig.5 Number of DNNs and the convergence of DDL-ESP algorithm
图6仿真了在不同学习率lr情况下,DDL-ESP算法的时延增益,其中设置DNN的数量=8。同理可知,随着时间的不断推移,当lr=0.01时,所提出的DDL-ESP算法最终同样能以大约为98%的时延增益逐渐逼近穷举法所产生的全局最优解。当学习率lr分别为0.000 1,0.001与0.01时,可以看出,适当地增大学习率lr能加快DDL-ESP算法的收敛速度。对比于学习率lr分别为0.000 1与0.001,当lr=0.01时,所提算法分别能提高平均时延增益0.058%与0.015%。当lr=0.1时,数据表明过大的学习率lr值不但不能使算法收敛,并且对比于lr=0.01所得到的时延增益反而降低大约0.136%。其产生的主要原因在于,在DNN训练过程中过大的lr值容易导致所使用的梯度下降算法在接近最优解附近来回震荡,导致算法无法准确地收敛到最优解,从而导致时延增益曲线出现不收敛现象且时延增益相对较低。但值得注意的是,如果学习率lr值过小,意味着算法在学习过程中将需要更多的训练时间找到最优解。同理,在实际运用中,学习率lr值的设置需要结合数据集的特征及大量的实验才能使训练时间与算法收敛性达到最佳状态。
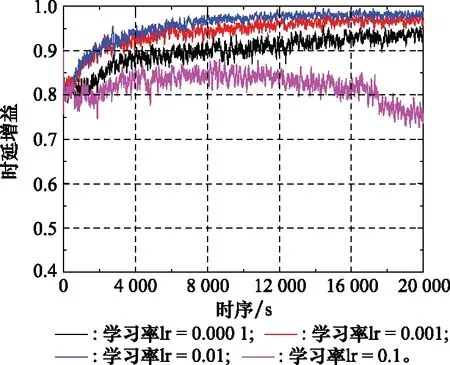
图6 学习率lr与DDL-ESP算法收敛性Fig.6 Learning rate lr and the convergence of DDL-ESP algorithm
为了验证所提算法的可行性,本文考虑了3种基准对比算法,分别为云服务方案、边缘云服务方案与穷举法。其中,在云服务方案中,所有用户的服务请求通过本地SBS上传至ASP的云服务器,因此边缘云不为任何用户提供服务。相反,在边缘云方案中,ASP在每一个边缘云放置用户需要的所有服务,云服务器将不会为任何用户提供服务。对比于DDL-ESP算法而言,穷举法将列举出所有可能的服务放置行为,然后挑选出使得优化目标最小化的服务放置行为作为当前时刻最优的边缘服务放置行为()。显然,在任意时刻,穷举法都能获取全局最优解,但该算法的时间复杂度将随着边缘云及服务种类的数量增加成指数式增长,不利于在环境实时变化的动态网络中应用。
图7仿真了在不同折扣因子值情况下,4种方案所得到的平均用户加权时延。可以看出,随着折扣因子的不断增大,DDL-ESP算法所产生的平均用户加权时延比穷举法所产生的全局最优解约高23.3 ms。在不同值情形下,通过对DDL-ESP算法与其他两种方案加权时延的数值差进行相加并求平均值,然后除以所有用户,得出DDL-ESP算法能够分别将平均用户加权时延降低为0.31 s与0.48 s。此外还可以看出,当≤001时,4种方案所产生的平均用户加权随着折扣因子的增大出现缓慢增长。其原因在于,当相对较小时,意味着ASP将在边缘云部署更多的服务,从而保障用户服务质量,也即牺牲更多的服务放置成本换取更好的服务质量。但≥001时,ASP为节约服务放置的部署成本,选择牺牲用户服务质量,从而导致用户的加权时延急速增大。因此,在实际运用中,ASP如果想节约服务放置的部署成本或者为用户提供更好的服务质量,都可以通过调控折扣因子值来完成。如果ASP既要保持用户服务质量不低于某一阈值的情况下降低其边缘服务部署成本,显然需要结合用户的服务请求密度及采集大量的用户数据等才能达到部署成本与服务质量相对折中的状态。
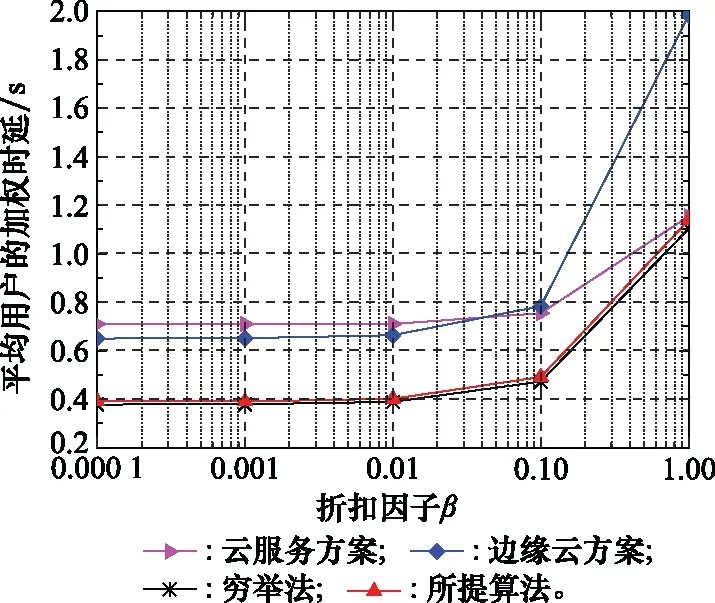
图7 折扣因子β与用户的加权时延Fig.7 Discount factor β and users’weighted delay
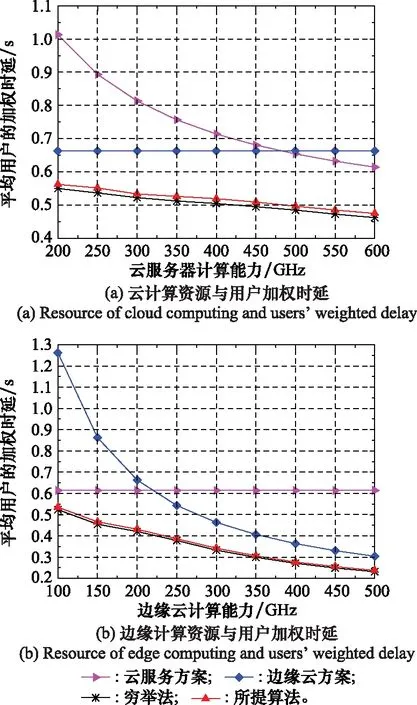
图8 边云计算资源与用户加权时延Fig.8 Resource of edge-cloud computing and users’weighted delay
结合图8(a)与图8(b)可知,虽然所提算法得到的平均用户加权时延高于穷举法,但是算法时间复杂度却远低于穷举法,使得所提算法的运行时间远低于穷举法。该结论将在图9进行验证分析。对比于其他两种算法,虽然所提算法的复杂度相对较高,但可以大幅度降低平均用户的加权时延,提高用户的服务质量。显然,所提算法不仅克服了云服务与边缘云方案容易导致用户的服务体验降低问题,而且解决了穷举法时间复杂度过高问题。
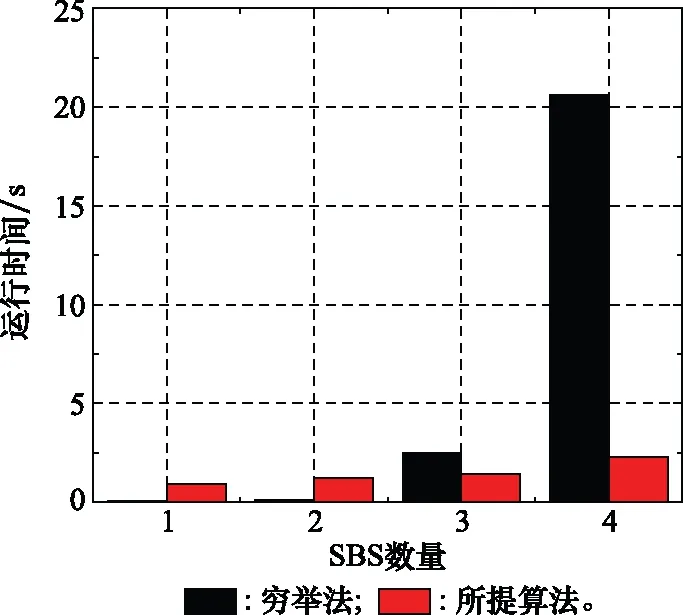
图9 平均运行时间Fig.9 Average running time
为进一步验证所提出的算法在放置行为生成过程中需要的运行时间与穷举法的运行时间的差异,仿真了不同SBS数量下两种算法的运行时间,如图9所示。本文设置每个SBS服务的用户数相等。从图9可以看出,随着SBS数量的不断增加,两种算法所需的平均运行时间也随之变大。需要注意的是,穷举法所需要的运行时间随着SBS数量的不断增加,呈现指数式增长。显然在实际的多用户多基站的边缘计算网络中,该方法不利于处理最优的服务放置行为生成过程。对比于穷举法,所提算法增加了3.47%的用户加权时延,但所提的DDL-ESP算法在运行时间上远低于穷举法,且每个用户的平均运行时间缩短了0.29 s。
6 结 论
为了满足MEC网络中多用户服务放置的需要,同时降低ASP的服务放置成本,提出了一种基于DDL的边缘服务放置策略。该策略考虑了用户服务请求时延以及服务放置成本两个因素,首先解决了计算资源分配问题,然后通过DDL解决了边缘服务放置问题。仿真结果表明,对比于云服务方案与边缘云方案,所提算法可以有效地降低平均用户加权时延,提高用户的服务质量。与穷举法相比,所提算法增加了少量加权时延,但大幅度缩短了算法的平均运行时间。在未来的工作中,将研究带有用户需求预测的移动边缘计算服务放置及小基站重叠覆盖对服务放置策略的影响等问题。

