多类型体系贡献率评估的综合问题研究
王茂桓, 刘泽苁, 梁浩哲, 张英朝,*, 孙 蕾
(1. 中山大学系统科学与工程学院, 广东 广州 510275; 2. 军事科学院系统工程研究院, 北京 100101)
0 引 言
随着智能化时代的到来,武器间的信息交互在战场上所产生的作用越来越举足轻重。这使得战争胜负不再由单一武器性能所决定,更加依赖于作战体系内部的有机协同。因此,着眼于体系视角评估和分析武器装备,是体系化战争背景下的一个重要评估思想变化。在武器装备规划论证时,必须考察装备是否能适应未来的军事能力要求,必须充分考虑装备是否能有效纳入现有装备体系中并形成有效战斗力,必须分析评估装备对现有体系形成的涌现效益。简言之,必须充分分析把握装备对现有体系的影响作用。为了有效评估这种影响效益,我军创新性提出“体系贡献率”的概念。由此,评价装备对体系的贡献率成为装备评价的重要标准。
目前,对体系贡献率的研究呈现出多个维度。
在理论研究维度,李怡勇等阐述了贡献率、体系对抗等问题概念,研究并提出了体系贡献率研究的一般特点;吕惠文等提出了体系贡献率的多层评估指标体系;李小波等对体系贡献率的问题域、技术域等方面进行详细论述,并综述了国内外研究的进展;闫海港等提出了体系贡献率的6个评估维度,并分析了体系贡献率在全寿命周期的运用;Liu等对4种贡献率的描述形式进行对比分析;卜广志提出了AOE模型,建立装备、活动、效果之间的描述,分析装备对作战体系的贡献机理,进而支撑贡献率评估建模。
在评估对象维度,可以分成对装备体系作战能力、对装备体系作战效能、对装备体系结构优化、对装备体系技术贡献等方面的研究。
在评估应用背景维度,可以分为对具体的交战背景的研究、对装备计划规划的研究、对装备项目(群)遴选的研究。
在方法使用的维度,可以分为从体系结构的视角,运用作战网络进行评估分析;从任务执行的视角,运用仿真、探索性分析、系统动力学等方法技术进行分析;从指标建模的角度,运用层次分析法(analytic hierarchy process, AHP)、网络分析法(analytic network process, ANP)、数据包络分析(data envelopment analysis, DEA)、结构方程模型(structural equation modeling, SEM)、逼近理想解排序法(technique for order preference by similarity to an ideal solution, TOPSIS)、证据理论、贝叶斯网络、粗糙集等方法进行分析。
综合看来,目前对装备体系贡献率的研究已形成初步成果。但随着技术发展和战场形式的变化,装备的运用产生了巨大变化,信息力成为致胜的主导要素,这种“隐式”效益成为未来装备规划中不可忽略的要素。而体系问题作为一类复杂系统问题,也使得决策者不得不从多个维度进行全面充分的分析。这些现象使得体系贡献率的类型逐渐多元化。
在分析过程中产生的多个贡献率结果,通常采用线性加权求和或是取极值的方式进行。然而,由于贡献率自身的数学含义,采用以上方式进行综合,其结果会对评估结论产生重大影响。因此,必须对贡献率数理内涵做进一步梳理,研究出合适的综合分析方法。
为了解释体系贡献率的综合问题,本文首先对多类型贡献率的产生机理进行分析,并进一步对其多样化与层次化特性进行研究,最终给出相应的综合模型。本文的贡献如下:
(1) 通过对贡献率的机理进行研究,得出了3种产生多样化类型的原因;
(2) 在目标多样化和目标层次化特性上,运用数理分析研究其综合计算问题;
(3) 提出了3种适宜解决多类型贡献率综合的求解分析模型。
本文的结构如下:第1节论述多类型体系贡献率的产生原因;第2节论述由多样化特性产生的体系贡献率不可线性综合的原因;第3节阐释层次化特性产生的体系贡献率不可线性综合的原因;第4节给出相应的综合模型;第5节对本文工作进行总结,并展望下一步研究工作。
1 多类型体系贡献率概述
1.1 体系贡献率概念及综合
贡献率可以描述如下:假设目标背景为,(·)是在该背景下的评估函数。设原装备体系为,经过建设规划后,装备体系变化为′,假设到′的变化为。使用符号⊕表示变化的加法,于是′=⊕。对于变化,其体系贡献率的基本形式如下:
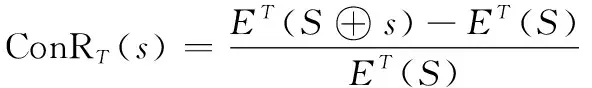
(1)
值得说明的是,这种变化不仅是增添装备,还包含替换和退役装备。因此,广义上,装备体系贡献率表征原体系的变化所产生的作用程度。
在分析过程中,产生的多种类型体系贡献率通常采用线性加权求和或是取极值的方式进行综合,求解模型如下:
(1) 加权和假设ConR表示不同类型的贡献率结果,表示对应的权值,于是综合贡献率表达式为
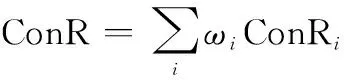
(2)
其中,均值是加权和的一种特殊形式。
(2) 取极值
假设ConR表示不同类型的贡献率结果,于是综合贡献率表达式为
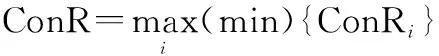
(3)
事实上,取极值的计算方式可以看做一种特殊的线性加权求和,对于式(3)可以描述如下:
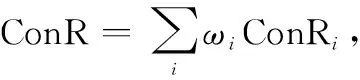
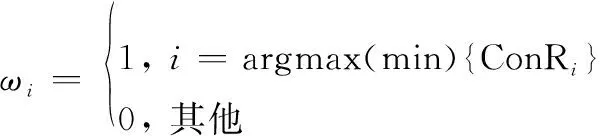
(4)
因此,上述综合方式归根到底是在讨论多类型体系贡献率的线性加权求和问题。
1.2 多类型体系贡献率产生机理
多类型贡献率的产生有以下3个主要原因:
(1) 评估目标的多样化
体系贡献率存在多样化的评估对象,当决策者期望较为全面地了解一个装备方案时,会从多个维度进行分析,这产生了多个决策目标,不同目标对应不同类型的贡献率。由此,产生多类型体系贡献率。多样化评估目标示意图如图1所示。
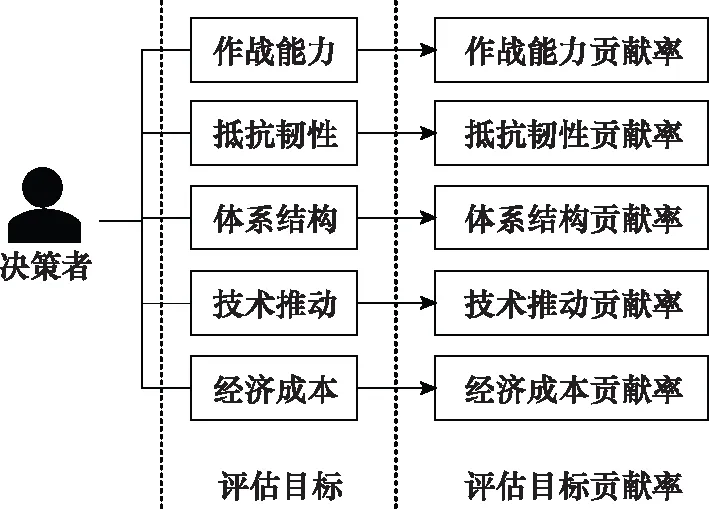
图1 多样化评估目标示意图Fig.1 Diagram of diversified evaluation targets
(2) 目标层次化分解
一个顶层目标可以分解为多个信息粒度更高的因素,其贡献率的产生来源于各因素的作用。因此,一个顶层目标可以分解细化,转化成多个低一层的要素,各要素又会形成各自的贡献效果,从而形成多类型贡献率。目标分解示意图如图2所示。
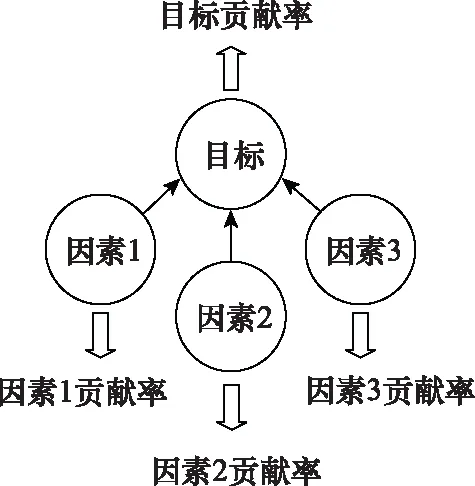
图2 目标分解示意图Fig.2 Diagram of target decomposition
(3) 多维度的贡献机理
评价对象可能从多个维度对体系产生贡献。体系的层次划分可以分为体系层、系统层、平台层、单元层4个层次,评估对象可能与同一层次上其他要素之间发生作用,包括单向影响和双向交互,从而呈现出横向的贡献。同时,评估对象自身的作用效果逐层涌现,形成纵向的贡献。
例如,研制生产某一型具有新型技术的装备,可能带动其他装备的技术进步,从而产生横向的推动。同时,该型装备自身的技术进步也在体系层面上展现,形成纵向的贡献。
评估对象的多维度贡献(见图3)机理所产生的不同类型的贡献率,彼此之间可能存在着交互关系,因此逻辑上不能直接线性加权综合。需要梳理不同类型贡献率之间的具体交互关系,从而选择合适的综合方法。
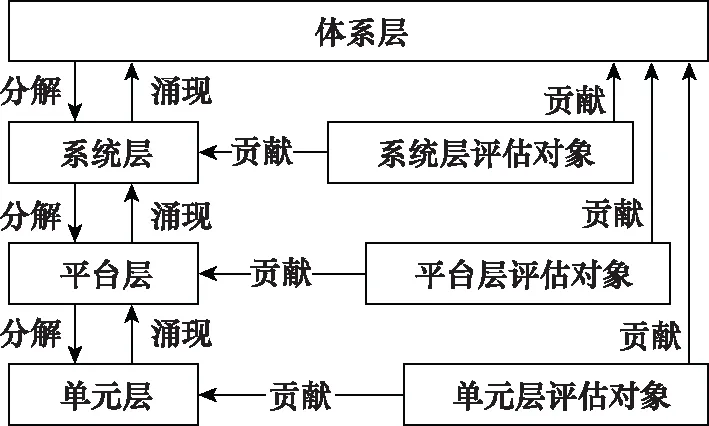
图3 评估对象的多维度贡献Fig.3 Multi-dimension contribution of evaluated objectives
从贡献率的多类型来源看,还需要进一步分析评估目标多样化和目标层次化对线性综合的影响。下文将通过数理分析说明通过线性加权求和对多类型体系贡献率综合的方法存在的局限性。
2 多样化目标特性
2.1 示敏性函数及其灵敏度作用
不同的评估目标,对应的评估标准与评估范式可能存在差异。在装备体系发生单位变化时,这样的差异可能使得各类型体系贡献率对变化的响应存在差异。
根据式(1),贡献率可以表示如下:
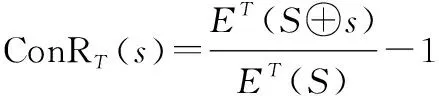
(5)
可以得到,贡献率的大小完全由变化前后体系的评价值的比值决定。
假设定义为单位变化,设映射
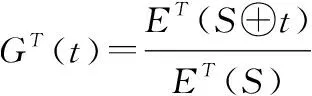
(6)
于是一个单位差下的贡献率变化为
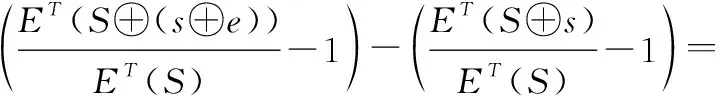
(7)
由于(·)的数值导数可以表示为
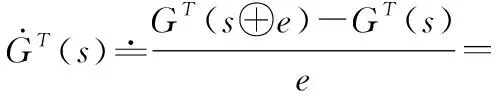
(8)

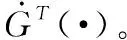
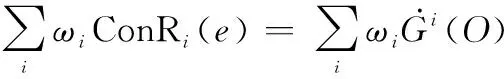
(9)
于是,其结果受到示敏性函数(·)在原点的灵敏度的影响,灵敏度差异会极大影响结果的倾向性。
以文献[12]为例,文献从能力、连接性、冗余性3个角度对贡献率进行描述,其部分结果如表1所示。从表中数据可知,3种贡献率的量级存在差异。冗余贡献率和连接贡献率的结果远远高于能力贡献率,若使用线性加权求和进行贡献率综合,则能力贡献率所产生的影响十分微弱。
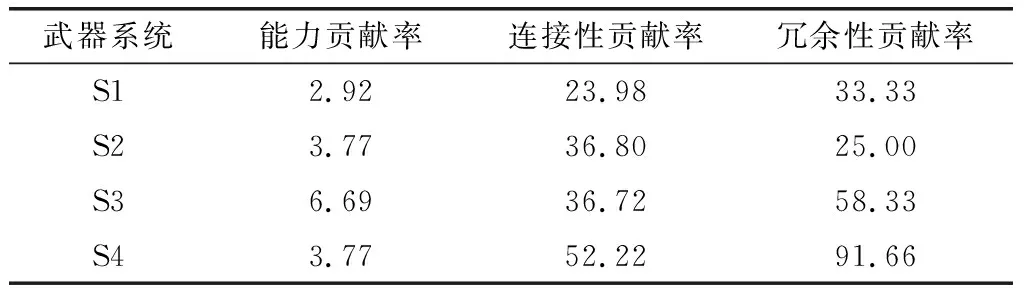
表1 文献[12]中的贡献率信息(节选)
因此,在进行多类型贡献率评估时,需要考虑其评价准则示敏性函数的灵敏度的影响。
2.2 规范化计算问题
不同类型的贡献率均为相同的度量单位,即为百分比。由于示敏性函数所表征的灵敏度差异,使得每个目标下贡献率的度量存在差异,导致贡献率评估目标之间的不可公度性。
为了消除不可公度性对评估造成的影响,在评价开始前需要规范化数据。然而,这样会失去贡献率本身的含义。
贡献率为收益型指标。假设为原指标数据,为规范化后的指标数据。数据规范化主要的处理方法具体如下:
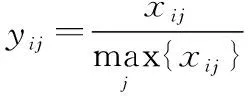
(10)
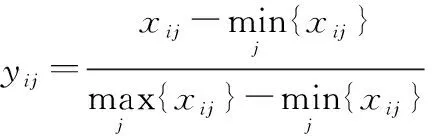
(11)
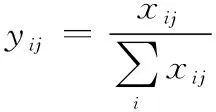
(12)
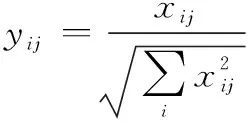
(13)
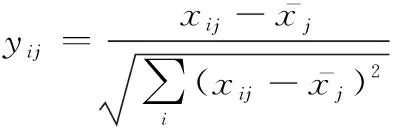
(14)
下面以式(10)为例进行说明。
针对目标所对应的贡献率为ConR,根据式(1),评价对象在下的贡献率可以描述为
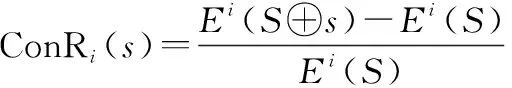
(15)
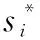
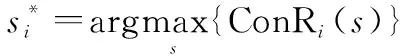
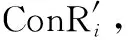
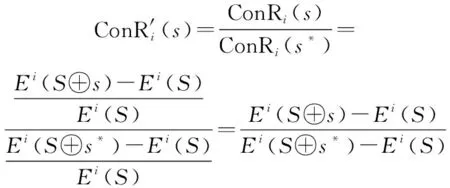
(16)
其他的规范化处理方法也可类似证明。
因此,在目标多样化特性下,所形成的多类型贡献率,由于其示敏性函数的灵敏度差异,以及规范化后的数学含义变化,使得其不能通过线性加权的方式进行综合。
3 目标层次化特性
体系贡献率评估目标具有分级层次特性,一个顶层指标可以进一步细分为粒度更细的指标,由此产生了多类型体系贡献率。以文献[32]为例,其将体系贡献率评估指标体系分为3个层级,如图4所示。
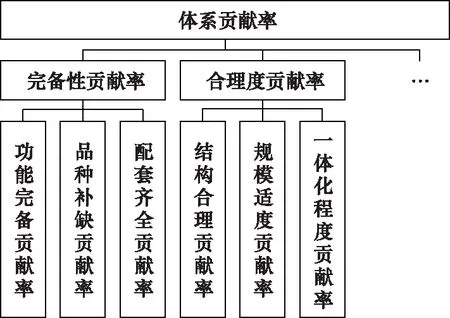
图4 文献[32]体系贡献率层次化指标体系(节选)Fig.4 Layer index system of contribution rate to system-of-systems in [32] (part)
与目标多样性特性不同,层次化引起的多类型体系贡献率,同层指标之间可以理解为是同纲规范的。因此,当下一层指标之间关系相互独立时,通常采用加权求和的形式进行综合。
但在贡献率问题中,下层指标贡献率的线性和不等价于指标线性和的贡献率,通过定理1证明。
对于某一顶层指标,可以分解为多个下一层指标(=1,2,…,;≥2),且同属于顶层指标范畴。若指标可以表征为的加权和,即
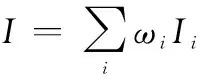
(17)
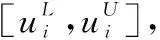
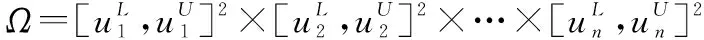
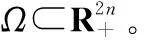
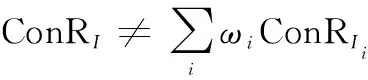
(18)
几乎处处成立。
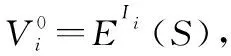
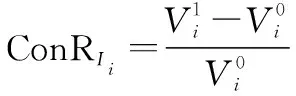
(19)
于是,得
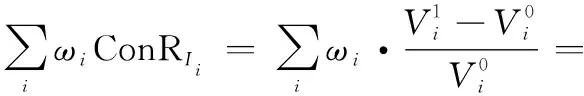
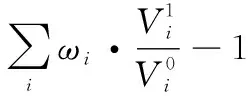
(20)
对于指标,原体系的评价结果为,新体系的评价结果为,根据式(17),有
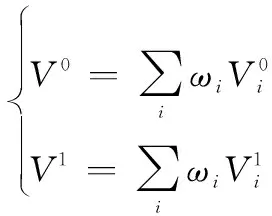
(21)
于是,得
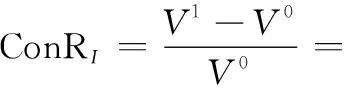
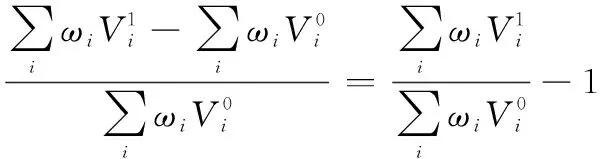
(22)
设
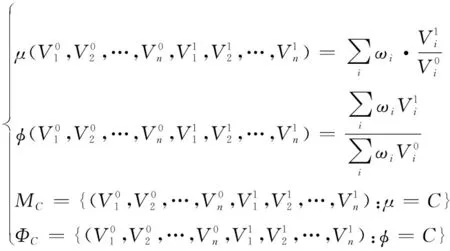
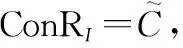
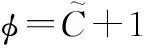
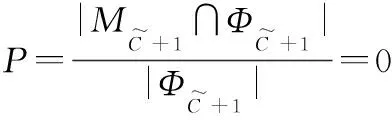
(23)
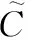
证毕
定理1说明在进行体系贡献率评估时,综合贡献率几乎不等于各项贡献率的线性加权求和。
值得一提的是,在贡献率评估过程中,所研究的评估空间可能为连续型空间,即存在指标取值为连续型;也可能为离散型空间,即所有指标取值均为离散值。虽然在不同的空间中,可能存在贡献率之和等于和的贡献率的情景,但是该场景很少,因此不能直接进行线性加权综合。
4 多类型贡献率评估的综合模型
对装备的体系贡献率评估的研究,需要把握以下几个要点:第一,需要落实到具体的支撑使命任务上,展现出决策者所关注的要素的增益,以展现装备是如何产生贡献的,供决策者有效分析;第二,体系贡献率是支持装备论证规划、建设发展的重要指标,因此需要能为装备发展重点方向选择、建设方案优化、方案遴选提供参考。
基于以上要点,结合前文提出的多类型体系贡献率综合存在的计算问题,本文提出3种多类型体系贡献率评估的综合模型。
为了进一步说明各模型的内容和使用场景,给定案例背景如下:在现有装备体系S上进行规划论证,并有8个可行方案S,S,…,S。需要对各个方案的能力效益进行分析。在进行规划遴选时,还需要考虑每个方案的技术效益。
4.1 过程终点求解模型
过程终点求解模型是指,在计算贡献率时,上层贡献率的结果不通过下层贡献率综合而得,应该在整个决策评估的最后进行求解。不同层的体系贡献率,应该分别进行求解。
这一求解模型适用于“分解-综合”的贡献率评估场景,可以处理层次化体系贡献率的多类型问题。但当多类型贡献率指标无法合理进行综合时,过程终点的求解模型便不适用。
过程终点求解模型案例
在某使命背景上,需要考虑侦查能力、指控能力、打击能力、防御能力4项能力要素,体系作战能力分解图如图5所示。
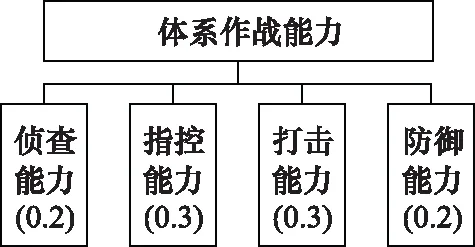
图5 体系能力分解图Fig.5 Decomposition of system-of-systems capability
于是,在该使命背景下,原装备体系的评价结果与可行备选方案的评价结果如表2所示,各项贡献率结果如表3所示。

表2 体系能力评价结果

表3 体系能力贡献率评价结果
根据表3的结果,方案S的能力贡献率最大,其次是方案S,再次是方案S,其在侦查能力方面产生了巨大的提升。根据图5可知,指控能力和打击能力的提升影响效果更大,方案S在打击能力方面也获得了较大的提升,使得其相应的贡献率最大。
从结果上看,各项贡献率加权和并不等于能力贡献率的综合结果。逐级求解贡献率,可以很好展示每一个指标的增益情况。
4.2 基于多目标优化的求解模型
基于多目标优化的求解模型是将每类型贡献率作为一个评估的目标,运用多目标优化算法进行求解,找出相应的最优解。
多目标优化的最优解称为Pareto解,或称非支配解。对任何目标,非支配解均优于支配解。由于多目标特性,Pareto解通常为一个解集而非单一解。
多目标优化的求解模型,可以应用于多样化目标形成的多类型体系贡献率综合问题中。该求解模型的解集结果,可以给决策者更多的决策备择,使得决策者能依据偏好进行选择,避免了单一结果形成的偏颇性。同时,由于多目标优化关注于目标结果本身,因此可以运用在由于机理产生的多类型贡献率评估中。
然而,Pareto解无法得出每个方案的优劣对比,因此依赖决策者自身进行更为细化的分析。
多目标优化的方案获取案例
在计算出使命任务下对应的作战能力贡献率的结果,并分析每个方案的技术效益,其技术贡献率的结果如表4所示。在众多方案中,决策者需进一步根据已有结果筛选出可行的方案集合。通过多目标优化算法,决策者可以获得一组非支配的方案群。该方案群的Pareto解如图6所示,因此最终共筛选的方案群为{S,S,S,S,S}。

表4 各方案技术贡献率评价结果
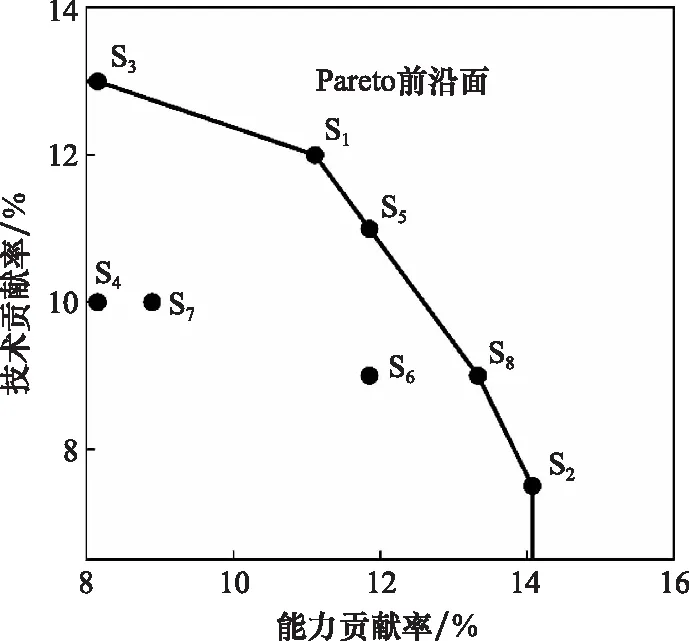
图6 Pareto解示意图Fig.6 Diagram of Pareto solutions
4.3 基于贴合度的求解模型
基于贴合度的评估方法主要有TOPSIS、VIKOR、灰色关联分析等,这类方法的主要思想是确定参考方案,计算各个方案与参考方案之间的贴合程度或者靠近程度。
运用基于贴合度的求解模型,是将多个贡献率类型看做方案不同的指标,由此设置参考方案,并计算各方案与该目标方案之间各类贡献率的贴合度。
基于贴合度的求解方法存在逆序问题,即备选方案变化时,各个方案之间的优劣对比结果可能发生变化。这一现象是由于方案变化时参考方案的变化造成的。为了避免逆序问题,可以人为设定参考方案的信息。
基于贴合度的求解方法获得的结果,不再以贡献率的形式进行展现,而是方案之间优劣信息的比较结果。贡献率评估的目的,是为了揭示装备方案对体系的效益,从而对装备方案进行排序。从结果上看,基于贴合度的求解方式具有适用性。
基于贴合度的求解方案,适用于多样化目标构成的多类型贡献率综合问题。同时,基于贴合度的求解能够包容研究对象复杂内在交互,使得方案通过参考方案进行整体性比较,因此也可以应用于多维度贡献机理形成的多类型贡献率综合情景。
基于TOPSIS方法评估遴选案例
在案例2中,决策者获得了可行的备选方案群{S,S,S,S,S}。共包含5个非支配的方案,但还无法获得方案之间的优劣。因此需要进一步分析。在本案例中,采用TOPSIS方法在方案之间进行对比排序。
将能力贡献率与技术贡献率作为方案的两个参数。为了避免逆序问题,人为给定正理想解的两项贡献率值为20%,负理想解的两项贡献率值为0%。这里给定能力的权重为0.6,技术的权重为0.4。由此,求解出各方案的贴合度如表5所示。

表5 各方案贴合度
从结果上看,各方案的优劣排序如下:
Sffff
可以得到为最优方案。从各方案的体系贡献率结果中看,的能力表现和技术表现虽然均不是最优的,但相对均衡,因此更适合纳入建设规划中。相较之下,具有最高能力贡献率的的技术效益过低,拥有最高技术贡献率的的能力效益过低,两个方案均不够均衡,如图7所示,方案与处于最两端的“偏科”位置,因此并不适合纳入建设发展中。
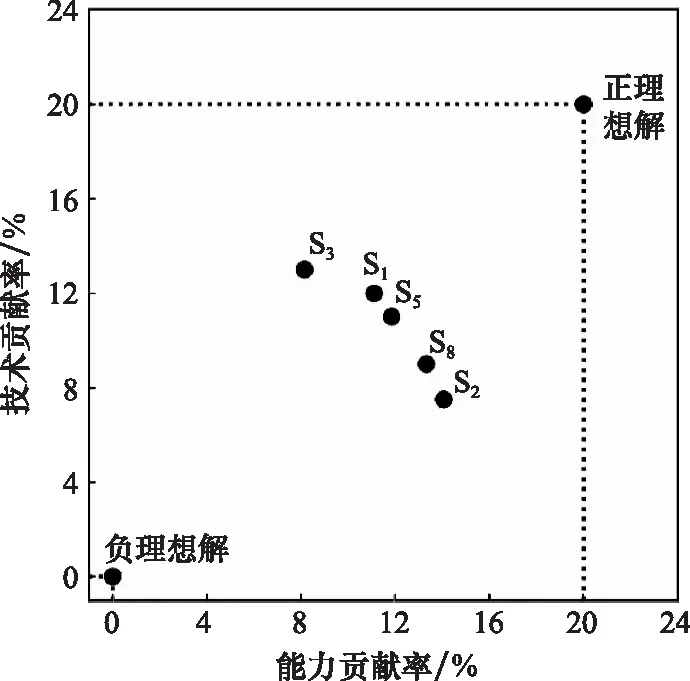
图7 TOPSIS示意图 Fig.7 Diagram of TOPSIS
从案例中可以看出,基于贴合度的方法可以兼顾多个目标需求,在方案间进行对比排序,为决策者遴选提供有效参考。
4.4 小结
根据多类型贡献率存在的不能通过线性加权进行综合的问题,本节提出了3种贡献率分析的模型:过程终点的求解模型、基于多目标优化的求解模型、基于贴合度的求解模型。并通过案例对3种模型进行详细说明。
根据上文分析,3种模型的优劣对比如表6所示。

表6 3种模型的对比
5 结束语
本文对多类型体系贡献率评估的综合问题进行了详细论述。说明了多类型贡献率的产生机理,包括评估目标的多样性、评估目标的层次性、产生机理的多维性,并进一步地对目标多样性和目标层次性两种原因进行数理分析。得出多类型贡献率不宜通过线性加权求和的形式进行综合的结论。
根据分析结果,提出了3种适宜的决策模型,包括过程终点模型、基于多目标优化的模型、基于贴合度的模型,并利用案例进行说明。最终对3种模型进行比较分析。
从本文分析来看,下一步可以引入灵敏度分析,进一步剖解各个类型贡献率之间的关系。同时,利用多目标决策理论的丰硕成果,对体系贡献率的评估进行进一步研究。

