基于低复杂度多项式乘法器的智能电能表椭圆曲线加密系统的设计

孙艳玲，邢宇，董贤光，翟晓卉，孙艳凤，张宏生

(1.国网山东省电力公司营销服务中心(计量中心)，济南 250001； 2.国网天津市电力公司蓟州供电分公司，天津 301900； 3.国网安徽省电力公司营销服务中心，合肥 230088)

0 引 言

近年来，随着国家电网的大规模建设，智能电网作为国家电网系统交通终端一环已经变得越发重要了[1-2]。由于智能电网的规模大，智能电能表与各个环节的网络存在很多的数据交换，这些数据交换在通信过程中隐存很多安全问题。如何恰当地设计智能电能表适应的安全系统是学术界和工业界一个当前的研究热点。

围绕智能电能表的安全问题已经在各个方面逐步展开[3-14]。故障预警系统的设计与开关在最近的文献[3]中有涉及。基于同态密码体制的智能电能表安全协议在文献[4]也有所报道。特别一提的是，文献[5-10]提出了关于智能电能表的数据安全采集和用户隐私保护问题。另外，文献[11-14]展示了智能电能表的安全算法和相关电路系统的研究。总体而言，对于如何给智能电能表配置适当的密码系统的研究还是有待继续加强。

椭圆曲线密码系统(Elliptic Curve Cryptography (ECC))安全问题如图1所示，由于能够提供比传统的密码系统更强的效果，现在已经成为智能电能表中的安全系统的理想候选者[15-19]。但是由于椭圆曲线密码系统的计算复杂度较大，并且智能电能表中还有其它的应用资源需要考虑[20]，目前，距离具体应用还有大量的研究工作。

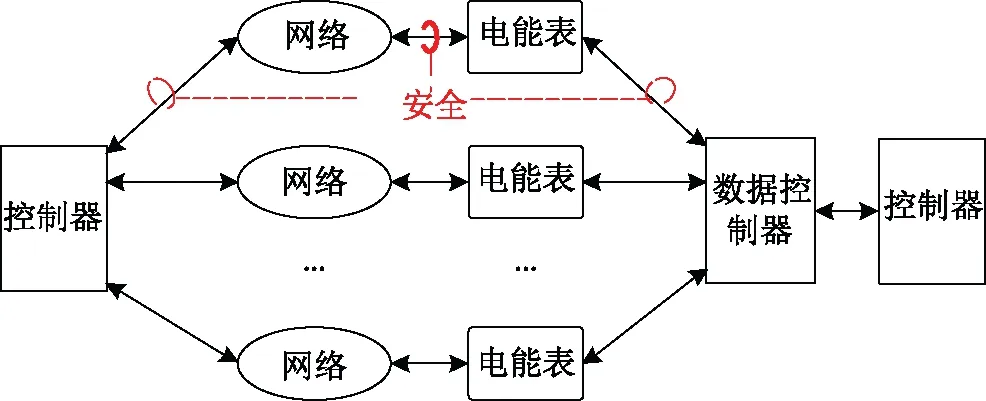
图1 智能电网中关系于数据通信系统的安全问题Fig.1 Security issues related to a typical data communication system within smart grid

在椭圆曲线密码系统中最主要的一个运算是基于椭圆曲线上的点加法运算，其中包含了在二进制域(GF(2m))中的加法、开方和乘法运算。在二进制有限域中加法和开方运算都能比较简单且快速，然而二进制有限域的乘法运算就显得比较复杂。这就使得密码系统占有资源面积变大、整体运算时间加长和运算速度减慢。文献[15-19]相继推荐了5个不可约多项式用于椭圆曲线密码器的计算，目前许多的研究工作集中在如何有效实现基于有限域GF(2m)上的乘法器。

基于有限域GF(2m)(二进制域)的多项式乘法器的实现可以主要分为三个基的运算：多项式基、正规基、和复基。对于椭圆曲线密码系统，特别是对于基于Koblitz曲线的密码器，基于正规基的多项式运算比其它两种基具有明显的效果：基于正规基的GF(2m)开方不需要任何硬件资源(只需要简单的移位)。但从另一面来说，一个有效的椭圆密码系统的实现也由一个密码系统中的主要运算单元的平行度所决定。因此，一个好的密码系统的实现需要同时优化底层结构和上层算法。

可编程逻辑器件(Field-Programmable Gate Array (FPGA) Device)具有操作简单和易于重复编程等特点，目前正在智能电网中越来越多地使用。文中根据这一发展趋势，提出了一种基于FPGA平台的新型椭圆曲线密码系统设计方式(适用智能电能表平台)。该设计从底层的乘法器设计创新出发，扩展到高层椭圆曲线的点计算。设计的结构在具体的FPGA器件上进行验证通过。该密码系统与现有的系统相比具有资源占用率低、速度快等特点。因而该设计系统值得在智能电网建设中大力推广并使用。

1 椭圆曲线密码系统

椭圆曲线密码系统是由文献[21]在1985年提出的。该系统的具体组成和数学背景陈述如下：

1.1 高斯正规基(Gaussian Normal Basis)

高斯正规基是正规基中的一种，由于它的运算复杂度低，近年来受到学术界越来越多的关注[22]。高斯正规基在GF(2m)域下的定义如下：

设N={β,β2, …,βn}，其中，n=2m-1;m是域的次数(β是一个正规基的基本单位)。那么对于任何的一个多项式A在该域下的表达式可为：

(1)

式中A=(a0,a1, ....,am-1)和ai∈GF(2)。高斯正规基的运算较普通的正规基要简单一点，但是它的开方运算仍然遵循不需要硬件资源这一规则。对于在该基下的两个多项式A和B，它们的乘积C可以表示为：

(2)

式中R(i,j), 0≤R(i,j)≤m-1, 1≤i≤m-1, 1≤j≤T表示乘法矩阵R(m-1)×T，该乘法矩阵的具体过程可参考文献[18]。

1.2 椭圆曲线(Koblitz曲线)

一般说来，一个Koblitz曲线可以通常表示为：

Ea,b:y2+xy=x3+ax2+b

(3)

式中a,b∈GF(2m)并且b≠0。取椭圆曲线上的两个点P和Q，使得Q=kP(k>1是整数)。那么，点P称为曲线的基点，Q称为结果点。一般来说，在曲线上点的运算包含点加运算和点乘运算(点乘运算可以转为点加运算)。

1.3 点加运算

有很多方法已经被提出来去有效地实现Koblitz椭圆曲线上的点加运算。其中最主要的包括Jacobian投影、标准投影和Lopez-Dahab投影方法。文中设计参考的是Lopez-Dahab投影方法，它的主要过程如下：

假设X、Y和Z表示曲线上的点的坐标，那么整个点加运算的过程如下：

(4)

(5)

(6)

通过这些点的依次运算，就可以得到椭圆曲线密码系统的综合运算过程。

2 椭圆曲线密码系统的新型设计方案

2.1 乘法器和加法器的新型混合设计方式

椭圆曲线密码系统的硬件实现一般都会用到底层基于GF(2m)域的高斯正规基乘法器和加法器。为了达到较好地实现效果如资源占用低、速度快等，乘法器一般都采用多位串行处理的方法(Digit-Serial)，如图2所示。图2中包含了一个乘法器的乘法核心单元和累加单元以取得最终的乘积(其中的一个输入是以分段的方式接入到乘法器核心单元里面)。累加单元则需要对这些分段得到的乘法结果进行累加并且输出最终结果。

图2 一个基于GF(2m)域的高斯正规基乘法器Fig.2 One Guassian normal basis multiplier based on GF(2m)

由于基于高斯正规基的开方运算是没有硬件资源消耗(只有位的位置转换)，那么有：

(7)

式中I1和I2为输入；I为输出。按照传统实现方法，式(7)需要先进行I2的开方运算，然后再进行下一步的乘法运算来取得最终结果。

为减少具体应用过程的计算延迟，文中提出一种新型的乘法器和加法器混合设计方法：即把这个开方运算合并到乘法运算里面(因开方只有位的移位而已)。这样，原来两个运算就可以合并成为一个新的单独运算，相对应的设计如图3所示。

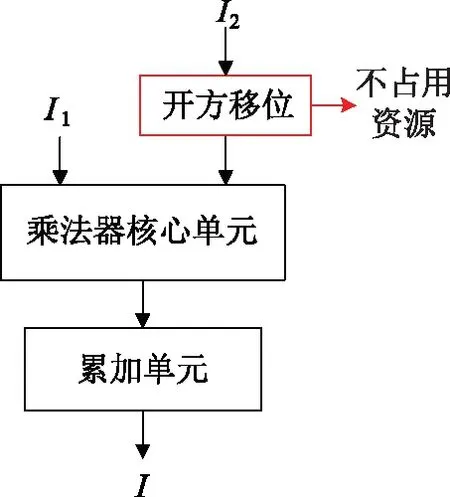
图3 混合结构的乘法器(新型设计)Fig.3 Hybrid structure based multiplier (new design)

如图3所示，由于开方的运算不占用资源，原先需要两个周期的运算(指乘法和开方)现在就可以在一个周期内完成。这样的设计安排将对整个密码系统的涉及到乘法和开方的运算进行优化。

同样，对于以下的运算方式：

I=(I1+I2)2

(8)

式中I1和I2为输入；I为输出。按照传统的实现方法，式(8)需要先进行I1和I2的加法运算，然后再进行下一步的开方运算。

为此，文章提出一种新的混合设计方法，即把这个开方运算合并到加法运算里面(开方只有位的移位而已)。这样原先的两个运算就可以转换成为一个单独的运算如图4所示。

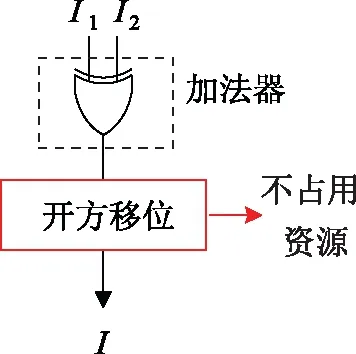
图4 新的混合运算加法器Fig.4 New hybrid adder

为验证文中提出的混合结构的优势，文章对图3和图4的混合结构采用硬件描述语言(Very High-Speed Integrated Circuit Hardware Description Language, VHDL)进行建模仿真。这两个设计在FPGA(Altera Cyclone II芯片)平台上进行仿真验证，并且通过Altera Quartus II 12.1 软件测得结果。本设计采用m=100作测试，所得的FPGA结果(主要指占用逻辑资源)如表1所示。

表1 FPGA测试结果Tab.1 FPGA testing result

LE: Logic element，FPGA平台上的逻辑资源。

由表1可知，采取了混合结构的资源占有和非混合结构(FPGA平台上)是一样的。这显示本设计可以在具体算法中进行使用而不增加额外资源消耗。

2.2 椭圆曲线算法的新型优化

为了更好地融合所提出的混合乘法器和加法器结构，该设计将之前的算法式(4)～式(6)改进如下：

(9)

(10)

(11)

其中，H1=y2Z12，H2=A2和H3=B2这三个运算都可以用之前提出的混合结构来实现。

2.3 信号流程图

根据文献[18]，式(4)～式(6)椭圆曲线系统的整体运算，可以用图5的信号流程图来表示，如图5所示。

由图5中可以看到，整个椭圆曲线系统的算法运行可以由13个阶段组成，其中三个阶段的主要运行是乘法器(每个阶段有M+1个运算周期)。综合而言，乘法器的执行所占用时间远远大于其它运算所占用的时间。所以，整个椭圆曲线密码系统的计算时间实际上主要由乘法器的执行时间决定。

图5 信号流程图Fig.5 Signal flow chart

为降低密码系统的整个执行时间，文中采用所提出的新设计方式如式(9)～式(11)。如图6所示，文中采用的新型混合结构的椭圆曲线密码系统的整个算法的计算时间由之前的12个阶段减少到10个阶段。这样，整个算法的计算时间得以有效减少。此外，由于减少了2个计算阶段，相应的硬件控制环节和涉及的硬件资源消耗也会降低。

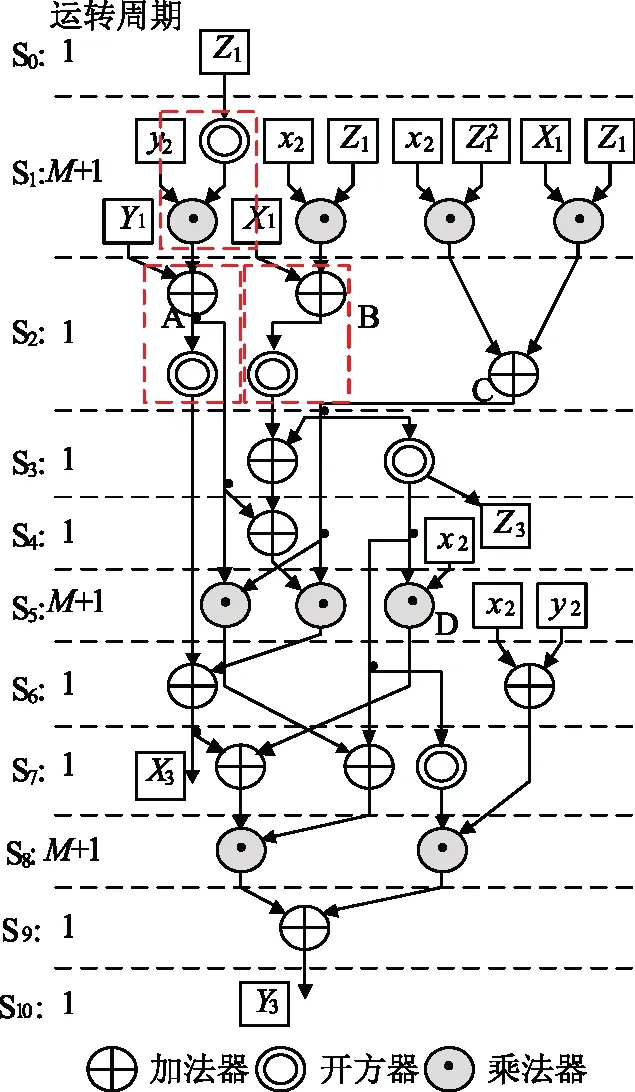
图6 新的信号流程图(虚线框内是混合结构)Fig.6 New signal flow chart (dotted block is the hybrid structure)

2.4 椭圆曲线密码系统的新型结构

该硬件结构是由图6的信号流程图直接印射而得，基于新的信号流程图上的椭圆曲线密码系统的新型硬件结构如图7所示。

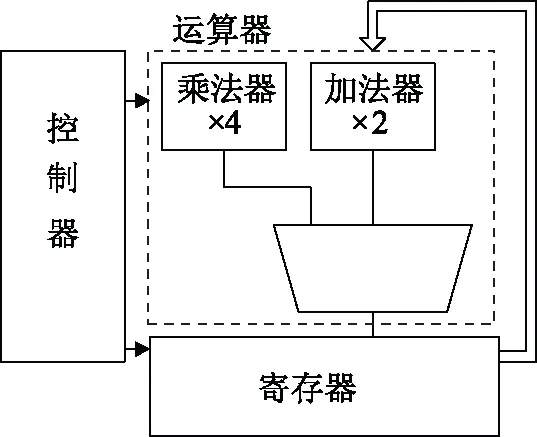
图7 最终的椭圆曲线密码系统架构Fig.7 Finalized structure for ECC

由于图6所示的整个的椭圆曲线密码系统需要4个乘法器和2个加法器，图7中的硬件结构主要由三大块组成：控制器、运算器和寄存器。控制器主要是产生相对应的控制信号以进行各个运算周期的调配。运算器则是包含了基本的运算单元如乘法器和加法器。寄存器主要的作用是进行各个运算周期之间的数据读入和读出。在具体的运行过程中，该三大块组件需要进行合理协调以得到正确结果。

3 FPGA平台上的测试和验证

为验证本设计的优异性能，设计好的结构如图7所示，用硬件描述语言(VHDL)进行编程建模。然后，所设计的结构在FPGA Altera Stratix II EP2S180F10 20C3芯片上进行测试和验证(在具体的测试中文章采用了m=163和m=233)。为展示本设计的优异性能，文章把所测试的结果与现有的文献[15-18]进行比较，结果展示在表2中。值得注意的是现有的文献主要报导了m=163的结果。但随着安全技术的进步，选择较大的m(与安全级别直接相关)将有更广泛的应用空间。

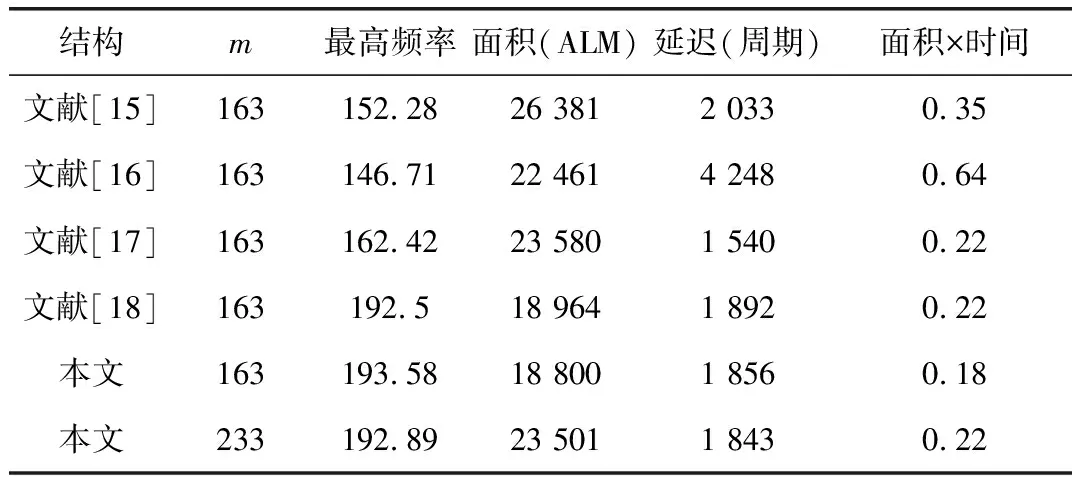
表2 FPGA平台测试结果比较Tab.2 Comparison of testing results on the FPGA platform

其中，面积的大小由ALM(Adaptive Logic Module，FPGA平台上的基本逻辑资源)的数量决定，最高频率的单位是MHz。m值的大小主要反应密码系统的安全级别(通常m越大系统越安全)。但是比较则是需要按相同的m值下的性能进行比较。现有文献[15-18]只报导了m=163时的结果。面积×时间=ALM的数量×(延迟周期/频率)。该参数通常用来衡量一个设计的综合面积和时间复杂度。

由表2可知，文章所提出的结构与之前的结构相比(相同的m值情况)具有更好的时间和资源利用效率。考虑到本设计也降低了椭圆曲线的计算周期，最终的时间使用改进力度将大幅超过之前报道的结果。同时，由于本设计采用了高斯基的多项式乘法器，本设计的最终占用逻辑资源与之前的设计相比也有较大幅度的降低(比如，在m=163情况下，相比文献[15-18]，文中设计有164-7581ALM的节省)。

除此之外，该设计也具有延迟时间低的特点(延迟时间=延迟周期/频率)。如表2所示，文中的频率比之前的结构具有较好的可比性。同时，该设计的延迟周期相对比较少。因此，该设计的综合延迟时间小于其它参考设计的延迟时间。

综合而言，文中所提出的椭圆曲线密码系统比之前的报道结果在时间和资源使用上都有较大幅度的改进。如表2所示，文中采用了面积×时间的综合复杂度指标来衡量各个方案的实现复杂度(该指标在其它参考文献中也被使用[15-18])。表2的数值表明文中设计的密码器比现有结构至少低了18.2%的综合复杂度(面积和时间上)。

除此之外，文章所设计的椭圆曲线密码系统结构也在智能电能表上进行验证测试。文中将所设计的结构嵌入智能电能表的测试平台进行输入输出测试。在进行1 000次的输入测试过程中，得到的输出结果与预想完全吻合(正确率达到100%)。

终上所述，该设计的新型椭圆曲线密码系统具有计算周期少、运算速度快和占用面积小等特点。因此，该设计方案比较适合于在智能电能表(或者类似平台)上的应用。考虑到智能电网同时还包括了其它方面的组成部件[20-23]，未来在这一方面的研究可以扩展到如何更好的与周围的部件协同运行。此外，考虑到智能电能表的具体应用环境(客户终端一环)，加强所设计密码系统的防攻击能力(如侧道攻击等)也是未来研究的一个主要方向。

4 结束语

文章提出了一种应用于智能电能表平台的新型椭圆密码系统设计方法。该密码系统的设计方案主要由底层的运算单元结构设计创新、上层算法流程的优化更新和最终新型硬件结构设计而组成。文中对所得到的相对应硬件结构进行了基于FPGA平台上的具体测试，并且取得了比之前文献所报导结构更好的结果。此外，该密码系统在具体的测试也验证了其在智能电能表中的应用可行性。

文章的具体创新点为：(1)提出新的有限域乘法器和加法器混合结构设计方式；(2)提出新的椭圆曲线算法实现方式；(3)提出基于新算法的椭圆曲线密码硬件设计方案和整体架构。文章所提出的密码系统新型设计方案具有延迟少、速度快和面积小等特点，适合在智能电网中的智能电能表上大规模推广使用。