基于流体力学原理的绝缘子覆雪三维数值模拟

胡玉耀，宗春郁，蒋兴良，咸日常，耿凯，杜钦君

（1.山东理工大学电气与电子工程学院，山东淄博 255000；2.输配电装备及系统安全与新技术国家重点实验室（重庆大学），重庆沙坪坝区 400044；3.山东汇能电气有限公司，山东淄博 255089）

由于我国负荷中心和能源中心分布不平衡，为实现大范围的资源优化配置，满足日益增长的电力需求，建设了多条特高压交、直流输电线路.截至2020 年3 月，我国已有10 条交流、15 条直流特高压输电线路投入运行.特高压输电线路在输送容量、电能损耗、经济性等方面具有明显优势，但由于输送距离远，不可避免地需要穿过覆冰积雪地区.绝缘子作为线路的重要设施，其电气特性对电力系统的安全起着决定性作用.在正常环境下，绝缘子的性能能够满足线路运行的要求.但在降雪天气，覆雪将严重降低绝缘子的电气强度［1］.

2013 年1 月，山东滨州地区突降大雪，积雪桥接了绝缘子迎风侧伞裙，随着温度回升，绝缘子发生多次闪络.2014 年2 月，南方地区迎来降雪天气，南方电网所辖地区10 kV 和110 kV 输电线路积覆湿雪，发生雪闪跳闸事故.2015 年5 月，黑龙江大兴安岭地区遭遇强降雪，导致66 kV、35 kV 以及10 kV 输电线路先后跳闸，部分城区断电.2020 年11 月18 日夜间至19 日白天，吉林省遭受有气象记录以来最强冻雨暴雪大风天气侵袭，受其影响，吉林长春、四平、松原等地区电网500 kV、220 kV 和10 kV 输电线路分别停运5 条、27条和320条，导致50万余户居民停电.2021年2 月15 日，美国得克萨斯州暴发雪灾，众多天然气、风能和火力发电厂因结冰停运，造成电力供应急剧下降，而为满足取暖需求用电量却激增，导致该州超400万人失去电力供应［2］.

绝缘子覆冰积雪降低其电气性能，关于覆冰（雪）绝缘子的闪络特性及放电发展过程国内外开展了大量的研究［3-8］，但对绝缘子积雪的规律研究相对匮乏.在寒冷环境条件下，过冷却水滴随气流运动并与输电线路等结构物碰撞形成覆冰积雪的过程是一个涉及流体力学、热力学、电磁学等多学科的复杂问题［9-10］.文献［11］提出用碰撞系数、捕获系数和冻结系数分别表征结构物覆冰积雪形成的过冷却水滴碰撞、捕获以及冻结过程.文献［12］基于流体力学原理，通过数值求解分别获取了悬垂绝缘子串的气流场分布、水滴运动轨迹，进而获得了过冷却水滴的整体碰撞系数.文献［13-14］采用区域分割方法将绝缘子表面划分为4 个局部区域，基于Lagrange 法，模拟了绝缘子外部气液两相流特性，分别计算了各区域的碰撞系数，但未得出三维覆冰积雪模型.

现阶段针对绝缘子覆雪增长特性及其电气性能的研究主要有三种方法［15-19］，即现场试验、人工模拟试验和数值模拟.现场试验能直观地反映绝缘子覆雪的真实状态，可有效地评估绝缘子自然覆雪后的电气性能，其结果可直接用于冰雪地区输电线路外绝缘的设计；但缺点是要求试验场所处于冰区，而且试验受气候条件制约，试验周期长.人工模拟试验克服了现场试验的缺点，试验环境参数可调且可重复，短期内可以获得大量的试验数据，便于研究绝缘子覆冰积雪的规律以及电气性能的变化趋势，但是人工模拟试验和现场试验之间的等效性仍需进一步研究.数值模拟方法不受试验设备、场地及气候条件的制约，可任意改变环境条件及绝缘子结构参数，而且能够真实地再现绝缘子的覆雪过程.

由于绝缘子的外形结构复杂，相同环境条件下绝缘子表面不同位置的碰撞系数不一，因此建立绝缘子覆雪三维数值模拟的关键在于如何获取雪晶颗粒局部碰撞系数.本文基于CFD 原理，采用数值模拟方法计算得到了XP-70绝缘子表面不同位置的颗粒局部碰撞系数；根据质量平衡和能量守恒方程，建立了绝缘子三维覆雪数值模型，得到了覆雪量与覆雪形态随时间的变化规律，研究了风速、液态水含量以及颗粒直径等参数对覆雪增长过程的影响，并通过人工气候室试验验证了模型的有效性.本文的研究期望推动绝缘子覆雪由人工或自然试验研究向数值模拟研究方向发展，并为后续构建雪闪模型提供支撑.

1 绝缘子及外流场模型建立

本文以XP-70 为研究对象，依据表1 的结构参数建立了如图1（a）所示的三维几何模型，边界条件设置如图1（b），计算域设定为5 000 mm×3 000 mm×3 000 mm.为避免计算过程中出现出口回流问题，使绝缘子串适当远离计算域出口.为准确模拟空气流场在绝缘子表面的热量传递情况，绝缘子表面网格尺寸加密至10-3m，绝缘子表面边界层首层网格厚度设置为10-6m，并以1.1的增长率向外延伸5层.

表1 XP-70绝缘子结构参数Tab.1 Structural parameters of XP-70 insulator

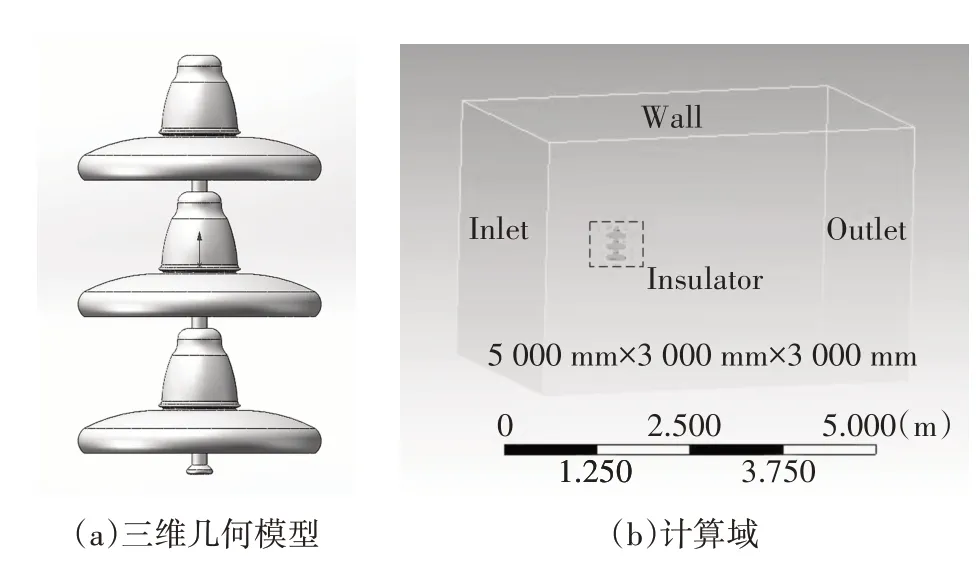
图1 计算模型建立Fig.1 Establishment of calculation model

2 绝缘子外流场特性分析

2.1 绝缘子周围两相流

绝缘子周围气流雷诺数较大且流速低，因此常被视为不可压缩的湍流流动.空气携带雪晶颗粒在绝缘子表面发生绕流，从本质上可以作为计算流体力学中的两相流进行处理.欧拉两相流模型在进行流场计算时，将流场中离散的颗粒视作连续流体.外流场特性可用如下方程进行表征［20-21］：

式中：ρa、va、Ta和κa分别是空气的密度、速度、静态温度和热导率；σij是应力张量；Ea是总能量；Ha是总熵量；τij是空气静态温度；t是时间；g是重力加速度.

气流绕过绝缘子形成绕流的过程中，绝缘子会影响气流的流动，导致流场中流体质点的速度和压力重新分布.图2、图3、图4 分别为绝缘子外流场特性图、绝缘子表面静压分布云图和绝缘子外流场速度矢量分布图.

如图2（a）所示，气流在远离绝缘子沿x正方向运动时，其流线是一组均匀分布的平行直线.当气流靠近绝缘子，受其扰动作用，原本平行的流线开始发生弯曲，直至气流绕过绝缘子后，弯曲的流线又恢复为平行状态.受黏滞性的影响，气流绕流过程中会在绝缘子表面形成边界层.当气流流近前驻点时，因绝缘子的扰动，气流速度逐渐降低，前驻点处的气流速度为0，如图2（b）所示.当气流从前驻点沿绝缘子表面向两侧继续流动，边界层随之发展变厚.边界层中的压力梯度使得在绕流过程中，气流压力随着速度的增大而逐渐降低（图3），此现象称为降压增速流动.但当气流绕过绝缘子迎风侧后，变成增压减速流动.气流向绝缘子背风侧流去时，增压减速更为严重，背风侧速度几乎为0［图2（b）］.受逆压梯度的影响，在绝缘子背风侧易形成涡流区，如图4所示.

图2 绝缘子外流场特性图Fig.2 Flow field characteristics around the insulator

图3 绝缘子表面静压分布云图Fig.3 Surface static pressure distribution of the insulator

图4 绝缘子外流场速度矢量分布图Fig.4 Velocity vector distribution of external flow field of the insulator

2.2 绝缘子表面局部碰撞系数

雪晶颗粒相的连续相和动量方程为［22］：

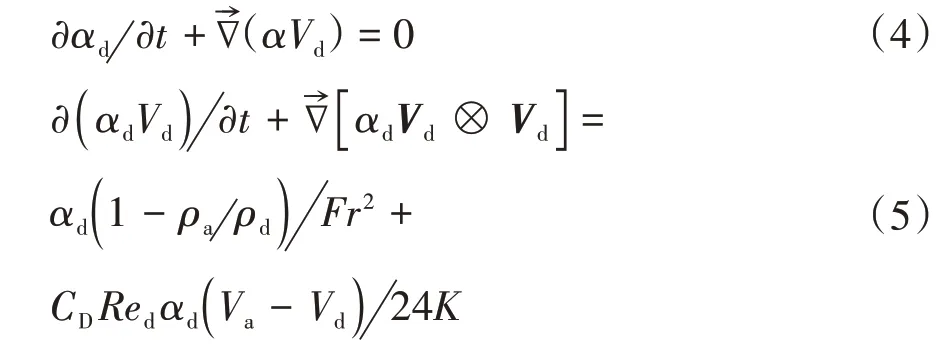
式中：αd、Vd和ρd分别是雪晶颗粒的体积分数、速度和密度；CD、Red、Fr和K分别是阻力系数、雷诺数、局部弗劳德数和惯性系数.

式中：Rd是颗粒直径；v∞是初始空气流速；μα是空气运动黏度；L∞是物体的特征长度；g∞是重力加速度.

覆雪过程中的雪晶颗粒直径一般比较小，因此在计算颗粒运动轨迹时做如下假设：

1）雪晶颗粒在随气流流动时外界环境介质参数恒定，且在绕流过程中不变形、不聚集、不破裂.

2）颗粒的初始运动速度与空气流速相等，且在绕流过程对空气流场无扰动作用.

3）除作用在颗粒上的重力和曳力外，其他力较小，可忽略不计.

图5 为绝缘子钢帽处和伞裙边缘处的雪晶颗粒运动轨迹.由于气流的黏性作用，颗粒在远离绝缘子时其轨迹与流线一致.当颗粒运动到绝缘子附近时，因颗粒的分子质量和运动惯性较大，颗粒偏离气体流线而与绝缘子碰撞.由于绝缘子结构复杂，不同位置处的气流特性不一，对颗粒的作用力也不一致，进而影响覆雪分布.因此有必要计算雪晶颗粒在绝缘子表面的局部碰撞系数.

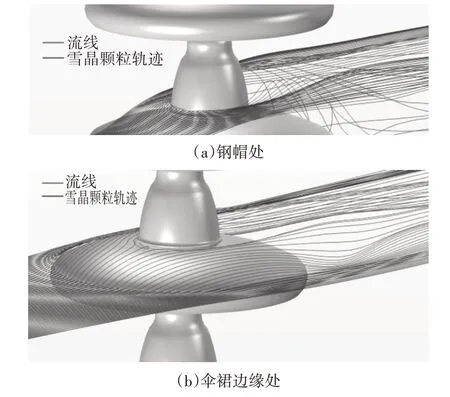
图5 雪晶颗粒运动轨迹图Fig.5 Trajectories of the snow particles

雪晶颗粒在风力作用下绕流绝缘子表面，部分颗粒因受到的气流曳力较小以致无法克服自身惯性作用而与绝缘子表面碰撞.在文献［11］中，碰撞系数定义为结构物实际积聚的雪晶颗粒质量与假定颗粒不绕过结构物而可能积聚的质量之比.上述定义适用于求解颗粒整体碰撞系数，而不适用于计算局部碰撞系数.本文绝缘子表面雪晶颗粒局部碰撞系数的计算方法如图6 所示.假设雪晶颗粒在远离绝缘子之前沿气流均匀分布，3 个相邻颗粒W1、W2、W3围成面积为S0的三角形，并均以V的初始速度向绝缘子运动，最终3 个颗粒被绝缘子捕获形成点，围成的微元面积为S1，对应的碰撞速度分别为V1、V2、V3，则此时对于绝缘子表面微元中心点P的局部碰撞系数β可以表示为：

图6 雪晶颗粒局部碰撞系数计算示意图Fig.6 The calculation method of local collision efficiency

当风速v为6 m/s、颗粒直径MVD（Median Vol⁃ume Diameter）为50 μm 时，绝缘子表面局部碰撞系数如图7所示.由图7可知：

图7 绝缘子表面局部碰撞系数分布Fig.7 Local collision coefficient distribution on insulator surface

1）钢帽前驻点处的局部碰撞系数最大，可达0.74，沿气流方向逐渐降低.

2）绝缘子伞裙表面颗粒碰撞特性呈现两种趋势，一是沿伞裙表面切线方向，局部碰撞系数的变化规律与钢帽类似；二是沿伞裙表面径向方向，从伞裙边缘到伞裙与钢帽交界处，局部碰撞系数逐渐减小，最大的碰撞系数为0.56.

为进一步对比分析绝缘子表面不同位置颗粒局部碰撞系数的差异，以中间绝缘子为例，在其表面定义了5个不同截面［图8（a）］，5个截面的碰撞系数分布情况如图8（b）所示.由图8（b）可看出：

图8 不同截面局部碰撞系数分布Fig.8 Local collision coefficient distribution for different sections

1）与绝缘子碰撞的雪晶颗粒主要集中在迎风侧伞裙边缘和钢帽处，而且所有截面的碰撞系数在迎风侧驻点处最大，沿流线方向的两侧逐渐减小.

2）截面B 的碰撞系数略高于截面A 对应的碰撞系数.这是由伞裙对气流的扰动作用所致，截面A 的等效直径较小，扰动作用明显，使得雪晶颗粒易随气流绕流通过绝缘子.与截面A 相比较，截面B 的气流稳定性较好，雪晶颗粒绕流数量较少，易被绝缘子表面捕获.

3）伞裙边缘（截面E）的碰撞率明显大于伞裙表面（截面C、截面D），这是因为伞裙边缘的倾斜角度远大于伞裙表面，雪晶颗粒对气流的跟随性较差，易偏离气体流线而与绝缘子碰撞，因此雪晶颗粒的碰撞系数和碰撞范围明显增大.

4）对于同处在伞裙表面的两个截面，截面D 的碰撞系数略高于截面C.这是因为与截面C 相比，截面D 的倾斜角度略大，故其碰撞系数和碰撞范围增大.

综上所述，根据局部碰撞系数大小就可以预测绝缘子表面不同位置的覆雪状态，即伞裙边缘和钢帽处覆雪最严重，因此下文重点分析截面E和截面B的颗粒局部碰撞特性.

绝缘子表面不同位置局部碰撞系数与环境参数有关.本文在温度为-10 ℃，液态水含量为0.6 g/m3的条件下，设置不同风速和颗粒直径，计算了绝缘子伞裙边缘（截面E）和钢帽处（截面B）的局部碰撞系数，结果如图9（a）、图9（b）所示.

由图9（a）可知，当MVD=50 μm 时，随着风速的增加，雪晶颗粒在伞裙边缘和钢帽处的碰撞系数逐渐增大.当风速为3 m/s 时，绝缘子钢帽处和伞裙边缘局部碰撞系数最大值分别为0.49 和0.42.而当风速增大到12 m/s 时，局部碰撞系数分别增至0.87 和0.66，分别增加了77.6%和57.1%.这是因为当风速增大时，随气流运动的雪晶颗粒速度也增大，导致气流曳力作用时间较短，雪晶颗粒来不及绕流更容易碰撞到绝缘子表面.

从图9（b）可以看出，当风速一定时，MVD 对局部碰撞系数的影响与图9（a）中风速对碰撞系数的影响规律相似，即随着MVD 的增加，两个截面的局部碰撞系数均增大.在MVD 从20 μm 增大至60 μm 的过程中，绝缘子钢帽处和伞裙边缘局部碰撞系数最大值分别从0.16 和0.14 增大至0.83 和0.63.同时，随着MVD 的增大，碰撞系数增长趋势变缓.其原因可以解释为：当颗粒直径较小时，气流曳力起主要作用，颗粒对气流的跟随性较好，易随气流绕过绝缘子；随着颗粒直径的增大，在惯性作用下，更多的颗粒与气流分离碰撞绝缘子表面，当颗粒直径增大到一定程度时，与绝缘子碰撞的颗粒数目达到饱和.

图9 不同环境因素对局部碰撞系数的影响Fig.9 Influence of different environmental factors on the local collision coefficient

3 绝缘子覆雪形态三维数值模拟

覆雪过程取决于绝缘子表面的质量守恒方程和热平衡方程［23］：

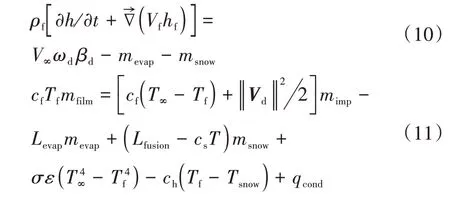
式中：ρf、hf、Vf、cf分别是雪层的密度、厚度、速度矢量和比热容；V∞是空气初始速度；ωd是空气中的液态水含量；βd是雪晶颗粒的碰撞系数；mevap是蒸发的液水质量；msnow是覆雪的液水质量；Tf是环境温度；T∞是空气远场温度；Levap是蒸发潜热；Lfusion是融化潜热；cs是雪晶的比热容；T是覆雪温度；σ是Stefan 常数；ε是雪层的辐射率；ch是雪层对流换热系数；Tsnow是雪层表面温度；qcond是传导热流量.

通过式（1）～（11）的求解，可以得到绝缘子表面每个网格单元上的覆雪质量.通过Jones 模型计算绝缘子覆雪密度后，就可以得到绝缘子表面的覆雪形状分布［24］.

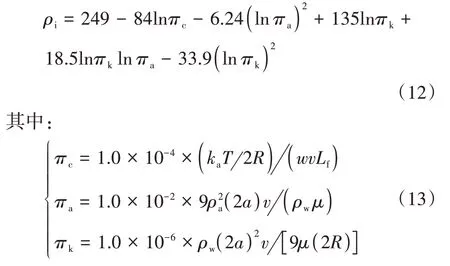
式中：ρi为雪晶的密度（kg/m3）；ka为空气的热导率，等于2.4mW/（m·K）；ρw、ρa分别为雪晶颗粒密度和空气密度（g/cm3）；μ为空气冻黏滞系数；a为雪晶颗粒半径（μm）；v为风速（m/s）；T为雪层表面与环境温差（℃）；w为空气中液水含量（g/cm3）；R为覆雪结构物半径（cm）；Lf为雪晶颗粒冻结释放的潜热（W/kg）.

当风速为6 m/s、MVD为50 μm、温度为-10℃、液态水含量为0.6 g/m3时，绝缘子表面覆雪分布随时间的变化如图10所示.

图10 绝缘子表面覆雪形态随时间的变化Fig.10 Variation of snow accretion on the insulator surface with time

从图10 中可以看出，覆雪主要形成在绝缘子的迎风侧，且随着覆雪时间的增加，绝缘子迎风侧伞裙边缘和钢帽处的覆雪量增加最为明显，绝缘子背风侧几乎没有覆雪存在，这与前述求解的绝缘子表面局部碰撞系数分布规律一致.

图11 为从绝缘子中轴线上提取的覆雪形态，可更加直观地看出相较于绝缘子背风侧，覆雪主要集中在绝缘子迎风侧伞裙边缘和钢帽处，而且随着时间的增加，覆雪厚度和范围逐渐增大.由前述分析可知，绝缘子背风侧受逆压梯度的影响，易形成涡流区，因此伞裙下表面的伞棱凹槽处有少量覆雪.

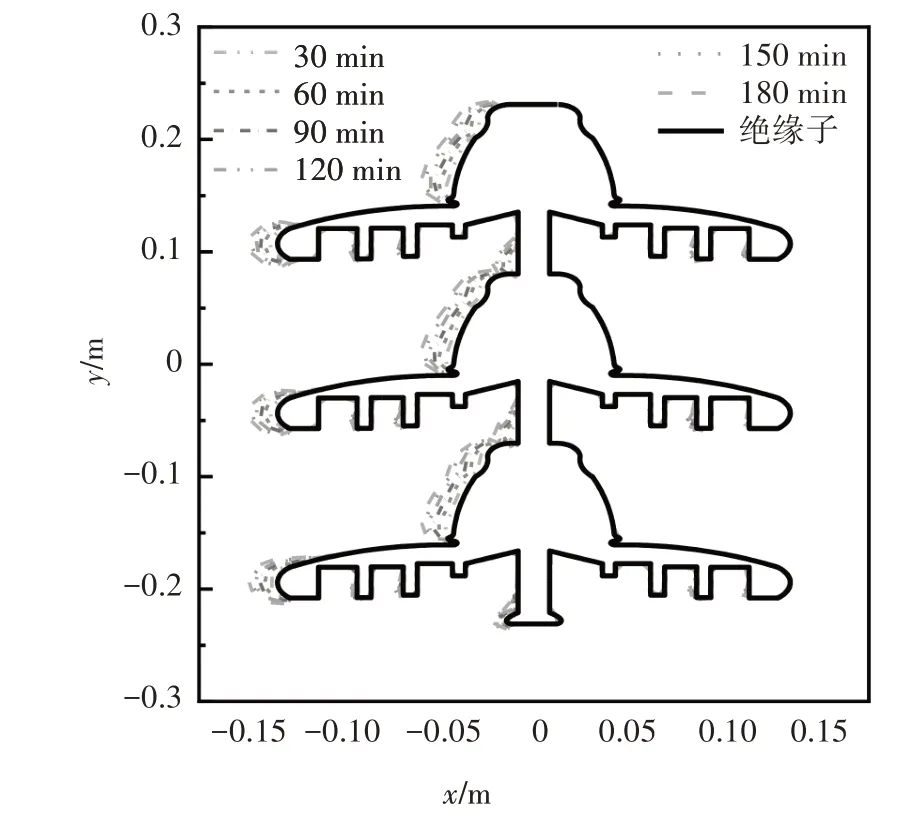
图11 绝缘子表面覆雪形态截面图Fig.11 Section diagram of snow accretion on insulator surface

4 不同环境条件下绝缘子的覆雪增长特性

自然条件下，绝缘子覆雪过程与周围环境参数密切相关.因此，本节重点研究覆雪环境参数包括风速（v）、颗粒直径（MVD）和液态水含量（LWC）对绝缘子覆雪量的影响.

4.1 风速的影响

为对比分析不同风速下绝缘子表面的覆雪增长特性，分别仿真计算了风速为3 m/s、6 m/s、12 m/s 时绝缘子的覆雪质量，结果如图12 所示.覆雪时间为120 min 时，3 种风速下绝缘子表面的覆雪形态如图13所示.

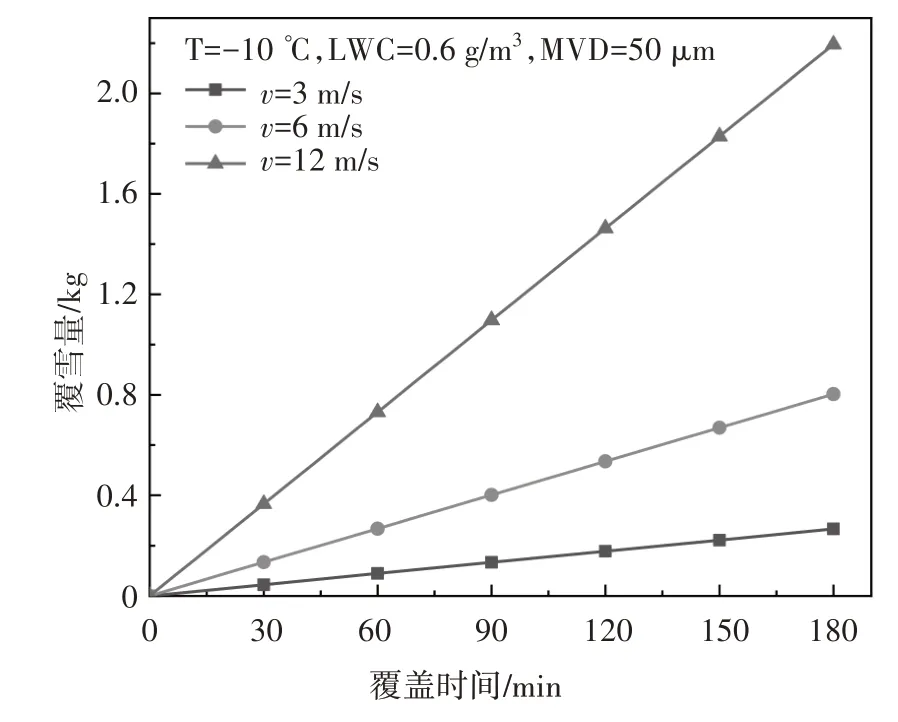
图12 风速对覆雪量的影响Fig.12 Influence of v on snowing weight

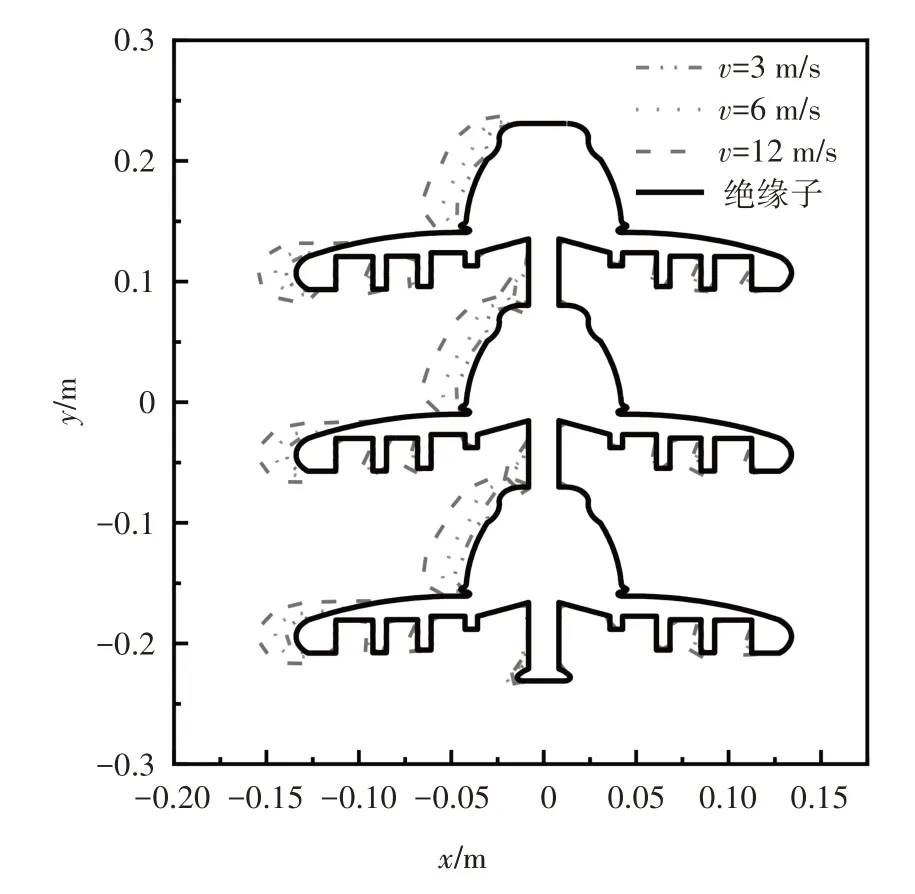
图13 不同风速下绝缘子表面覆雪形态截面图Fig.13 Section diagram of snow accretion on insulator surface under different variant wind velocity

由图12 可知，在不同风速下，绝缘子表面的覆雪量均随覆雪时间的增加而增大，且风速越大，覆雪越多.如，当覆雪时间为180 min、风速为3 m/s 时，绝缘子表面的覆雪量为0.27 kg；而当风速达到12 m/s时，覆雪量增至2.19 kg，增加了7倍之多.结合图12、图13 可以发现，随着风速的增大，绝缘子伞裙边缘和钢帽处相较于其他位置覆雪增长明显.这是由于在更大的风速下，单位时间内输送到绝缘子表面的雪晶颗粒增多，而且颗粒动能增大，易偏离气体流线与绝缘子表面碰撞.

4.2 颗粒直径的影响

当MVD 分别为20 μm、40 μm 和60 μm 时，覆雪量随覆雪时间的变化趋势如图14所示.不同MVD下绝缘子表面覆雪120 min后的形态如图15所示.

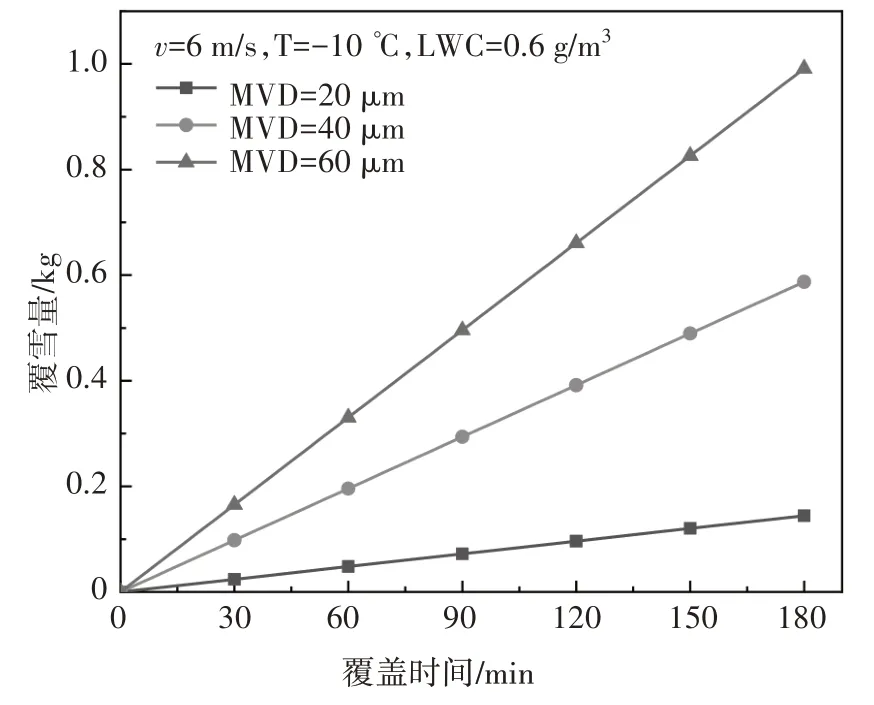
图14 MVD对覆雪量的影响Fig.14 Influence of MVD on snowing weight

图15 不同MVD下绝缘子表面覆雪形态截面图Fig.15 Section diagram of snow accretion on insulator surface under different MVD

由图14 和图15 可以看出，在相同的覆雪时间内，颗粒直径越大，绝缘子表面的覆雪量越多.例如，当覆雪时间为180 min，MVD 从20 μm 增大到60 μm时，绝缘子表面的覆雪量从0.14 kg 增至0.99 kg.MVD 越大即雪晶颗粒越大，其具有的动能越大，更容易碰撞到绝缘子表面，且雪晶颗粒在自身惯性作用下趋于保持原有运行轨迹，绕流雪晶颗粒数量减少，碰撞雪晶颗粒数增多.由于伞裙边缘和钢帽处局部碰撞系数最大，这两处覆雪最严重.

4.3 液态水含量的影响

当LWC 分别为0.3 g/m3、0.6 g/m3和1.2 g/m3时，覆雪量随时间的变化规律如图16所示.不同LWC 下绝缘子表面覆雪120 min后的形态如图17所示.

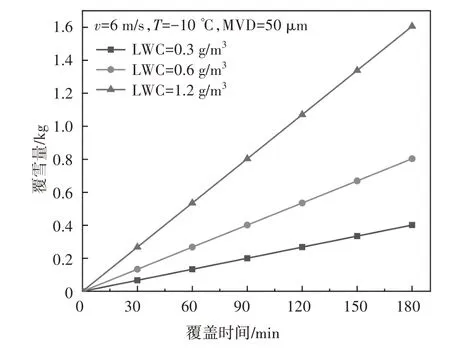
图16 LWC对覆雪量的影响Fig.16 Influence of LWC on snowing weight

图17 不同LWC下绝缘子表面覆雪形态截面图Fig.17 Section diagram of snow accretion on insulator surface under different LWC

如图16、图17所示，随着LWC的升高，绝缘子的覆雪量增大.例如，绝缘子覆雪180 min 后，当液态水含量为0.3 g/m3时，对应的覆雪量为0.40 kg；当液态水含量增大至1.2 g/m3，覆雪量为1.61 kg，增加了3倍.当空气中液态水含量增大时，相同时间内碰撞到绝缘子表面的雪晶颗粒数量会相应增加，导致覆雪量的增加.

5 试验验证

为验证绝缘子覆雪三维数值模型，在图18 所示的多功能人工气候室进行绝缘子覆雪试验.试验中采用粒径50 μm、液态水含量0.6 g/m3的雪晶颗粒，风速设为3 m/s、6 m/s，每隔0.5 h 测量一次绝缘子覆雪量，并与模型仿真数据进行对比，结果如图19 所示.图20所示为覆雪过程中绝缘子表面覆雪量.

图18 多功能人工气候试验室Fig.18 Multifunctional artificial climate chamber

图19 绝缘子人工试验覆雪形态图Fig.19 Snow morphology of artificial tests

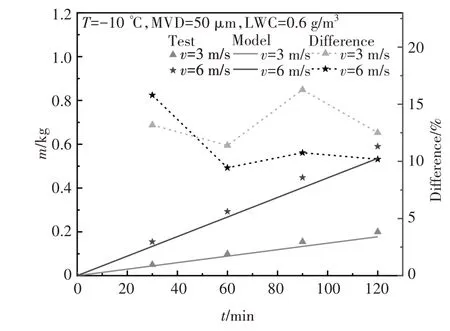
图20 数值模拟与人工试验覆雪量的比较Fig.20 Comparison of snow amount between numerical simulation and artificial tests

从试验结果可以看出，绝缘子串在多功能人工气候实验室中覆雪以后，覆雪主要沉积在绝缘子串迎风侧伞裙边缘，并且绝缘子钢帽迎风侧也有较多的积雪.对比发现，数值模拟中绝缘子表面积雪形态相对平滑，而多功能人工气候实验室内湿度较高，绝缘子表面积雪形态较为粗糙.

由图20 可知，数值模拟和人工试验结果均表明，绝缘子表面覆雪量随时间线性增长.此外，在本文研究范围内，两者之间的误差小于16.3%，表明该数值模型能够有效反映绝缘子表面覆雪过程.在积雪2 h内，人工试验中绝缘子表面覆雪量始终大于数值模拟覆雪量.主要原因有以下两个方面，一是多功能人工气候实验室是封闭环境，背风面可能会形成涡流，导致此处积雪.数值模拟中设置了出口边界，雪晶颗粒可以通过气流绕过绝缘子，背风面覆雪较少；二是由于多功能人工气候实验室内湿度较高，更加有利于雪晶颗粒的积聚和黏附.

6 结论

1）由于流体具有黏性，气流在绕流绝缘子时形成边界层，在其内部形成压力梯度.气流流近绝缘子前驻点处速度为0，沿流线方向速度增大，压力减小.当气流绕过绝缘子迎风侧时，转变成增压减速运动，背风侧速度几乎为0.

2）沿伞裙表面径向方向，从伞裙边缘到伞裙与钢帽交界处，局部碰撞系数逐渐减小；沿伞裙表面切线方向，从绝缘子迎风侧前驻点处沿气体流向向伞裙两侧降低，前驻点处局部碰撞系数最大，可达0.56.钢帽处的局部碰撞系数变化规律与伞裙表面类似，最大碰撞系数为0.74.

3）由于绝缘子钢帽和伞裙边缘处的局部碰撞系数最大，因此覆雪主要集中在这两个位置.受绝缘子背风侧逆压梯度形成的涡流区影响，绝缘子伞裙下表面凹槽处存在少量覆雪.

4）风速、颗粒直径和液态水含量通过影响雪晶颗粒的粒径、动能、惯性等因素，进而影响绝缘子的覆雪量，总体趋势是随着v、MVD和LWC的增大，覆雪量随之增大.180 min后，覆雪量最大可达2.19 kg.

5）数值模拟和人工试验结果表明，绝缘子迎风面伞裙边缘和钢帽处雪晶颗粒碰撞系数最高，积雪最严重.在不同环境条件下，两者误差小于16.3%，表明该仿真模型能够较好地模拟降雪过程.本文的研究期望推动绝缘子覆雪由试验研究向数值模拟研究方向发展.