虚拟同步控制的港口岸电电源阻抗建模及稳定性分析

陈辉，潘雄文，曾灿林，宋先勇，蒲贞洪，郭健，陈燕东†

（1.国网湖南省电力公司岳阳供电分公司，湖南岳阳 414000；2.湖南大学国家电能变换与控制工程技术研究中心，湖南长沙 410000）

水路运输作为传统的交通运输方式，对生态环境的影响极大.国际海事组织的数据显示，全世界以柴油为动力的各类舰船每年向大气排放1 000 万吨氮氧化物和850 万吨硫氧化物.由于常年采用柴油发电机作为浮吊的动力，油污、油烟、噪音给环境和大气造成严重影响.并且船舶在待闸锚泊期间，也需要通过辅机发电满足船舶值班、生活、照明设备等用电需求，持续排放出有毒有害物质，如硫化物、碳氧化物、PM2.5，这些严重影响了内陆湖泊的生态环境和浮吊产业的经济发展.我国内陆湖泊急需从现在低效、粗放、污染的柴油机供电体系逐步转变成洁净、高效、节约、多元、安全的现代化岸电供电体系［1-2］.

船舶岸电供电系统一般由10 kV 架空线路作为输入电压，经过变压器和变频器等装置输出400 V/50 Hz、440 V/60 Hz 和6.6 kV/60 Hz 三种电压等级的船舶供电电压.如图1 所示，本文主要针440 V/60 Hz的情况进行研究.为了增强惯性和阻尼，虚拟同步控制已逐渐应用于港口岸电供电电源［3］，以模拟同步机的外部特性，提供惯量和阻尼［4-7］.然而，随着大量电力电子化船舶负载接入岸电系统，恒功率负荷的负阻尼会削弱岸电电源的稳定裕度［8］，并可能导致系统振荡.因此，虚拟同步控制的港口岸电电源和船舶PWM 整流器负荷之间的控制相互作用有待进一步研究.

图1 低压港口岸电系统Fig.1 The low-voltage port shore power system

基于阻抗的稳定性分析是处理此类问题的有效方法，其基本原理是将广义奈奎斯特稳定判据（GNC）应用于系统的源荷阻抗比［9-15］.根据坐标系的不同，阻抗形式可分为如下几类：αβ轴阻抗，极坐标阻抗，序阻抗［15-16］和dq阻抗.其中，dq阻抗和序阻抗的研究较为广泛，考虑频率耦合后，序阻抗和dq阻抗都为二维矩阵，且基于序阻抗和dq阻抗的稳定性分析方法本质上是相同的［17］.然而，在dq坐标系下，三相平衡的变流器是线性时不变系统.因此可对各环节直接线性化，对所得的线性时不变模型进行拉普拉斯变换即可推导dq阻抗.因此，dq阻抗建模更简单，阻抗模型表达也更简洁.

目前，考虑锁相环（PLL）、直流电压等环节［18］，已有大量文献建立了变流器的dq阻抗模型.并且，文献［19］分析了逆变电源、PWM 整流器负荷和电网之间的控制作用，并从PWM 整流器的角度提出了抑制振荡的方法.文献［20］利用测量的dq阻抗探讨了逆变电源和PWM 整流器负荷之间的控制相互作用.此外，文献［21］建立了含dq轴控制器的虚拟同步机的dq阻抗模型.一方面，上述文献都忽略了控制延时和采样滤波器在dq坐标系和静止坐标系下的模型差异性.另一方面，由于港口供电电源存在多时间尺度控制特性，在各个频段的阻抗特性呈现显著的差异性.因此，在保证模型精度的前提下，可对基于虚拟同步控制的港口岸电电源进行分频段阻抗建模，进一步探索虚拟同步控制的港口岸电供电系统的小信号稳定性.

为解决上述问题，本文基于虚拟同步控制的港口岸电电源的多时间尺度控制特性，建立了其分频段dq阻抗模型.此外，通过阻抗测量［22-23］直接验证了所提阻抗模型的准确性和有效性.最后，本文基于所建dq阻抗模型和广义奈奎斯特稳定判据（GNC）分析了虚拟同步机控制的港口岸电系统的小信号稳定性.

1 虚拟同步控制的港口岸电系统

1.1 系统描述

图2 展示了基于虚拟同步控制的港口岸电供电系统的简化电路，其中，Lf、Rf和Cf分别为港口岸电电源逆变侧的交流侧滤波电感、电阻和电容；ea、eb和ec为岸电供电电源的输出电压；ia、ib和ic是岸电供电电源的电感电流；uab和ubc是PCC电压.

如图2 所示，Udc1是船舶PWM 整流器的直流侧电压；ia1、ib1和ic1是PWM 整流器的电感电流；Lf1、Rf1和Cd为PWM 整流器滤波电感、寄生电阻和直流侧电容.本文研究岸电电源与船舶负荷的控制交互作用，因此对实际系统进行简化.考虑到港口岸电电源的逆变器直流侧电压由强电网经二极管整流及电容滤波所得，视为常数；船舶负荷类型多样，含大量PWM整流器负荷（电动机负荷），在后文的分析中，考虑最恶劣的情况，即船舶负荷选取为PWM 整流器，忽略其他类型负荷（Rload，Lload）.港口岸电电源逆变侧的主电路可表示如下：

图2 440 V/60 Hz港口岸电供电系统的简化电路图Fig.2 The simplified circuit diagram of 440 V/60 Hz port shore power supply system

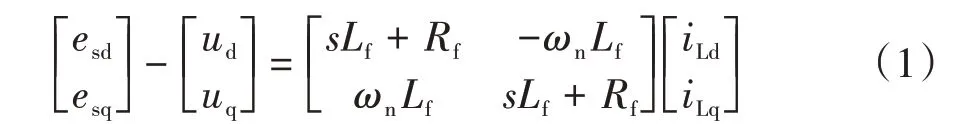
式中：esd，esq是港口岸电电源的端口电压；iLd，iLq为输出电流的dq分量；ud，uq是PCC电压的dq分量.

1.2 港口岸电电源的虚拟同步控制

港口岸电电源的逆变器采用虚拟同步控制，其有功环模拟了同步发电机的惯性和一次调频特性.

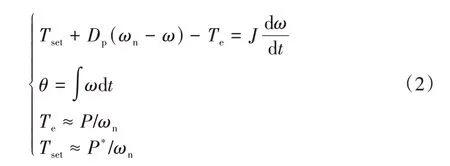
式中：J为虚拟转动惯量；ω和ωn分别为虚拟同步控制的输出角频率和额定角频率；Te是电磁转矩的给定值；Dp为有功阻尼系数；θ是VSG的相位.

无功环模拟同步电机的一次调压特性.

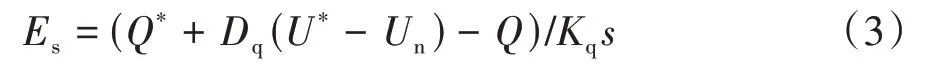
式中：Es为内电势有效值；Q*为瞬时输出无功功率Q的指令值；Dq是无功阻尼系数；Kq是无功环惯性系数；Un是电压幅值U的额定值.

其中，瞬时有功和无功功率的计算方式如下：

由无功环输出的电压幅值和有功环输出的相角可得αβ轴电压的给定值.

电压环采用准比例谐振控制器.

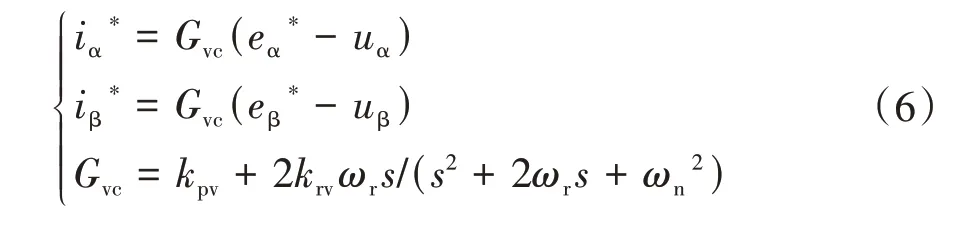
式中：kpv，krv和ωr分别为比例系数、谐振系数和低通截止频率.

电流环采用比例控制.

式中：kpi是电流控制器的比例系数.

2 港口岸电电源的阻抗建模

2.1 控制延时与采样滤波器的dq建模

控制延时在αβ轴下的小信号模型表示如下

根据静止坐标系到dq坐标系下传递函数的转换关系，可推导港口岸电电源控制延时的dq模型如式（9）所示.

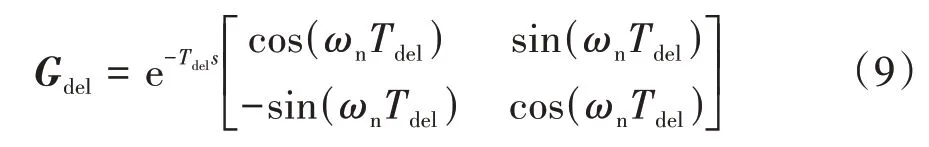
电压或电流采样低通滤波器的表达式如下：

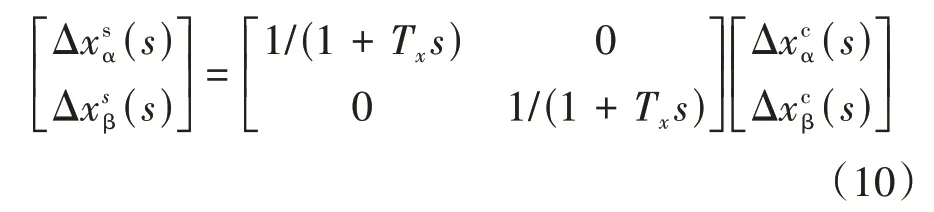
式中：x表示电流（i）或电压（v）；Tx=1/ωxc，ωxc是电压或电流信号低通滤波器的截止频率.

近似地，电压或电流的低通滤波器的dq模型可推导如式（11）所示.

2.2 虚拟同步控制的港口岸电电源的分频段dq 阻抗建模

岸电电源的虚拟同步控制具有多时间尺度特性，不同频段下对应不同的环节动态.在1～20 Hz 的低频段主要的动态环节为功率控制器与电压控制器；20～100 Hz 的中低频段主要动态环节为电压环、功率环和电流环；100 Hz 至几百赫兹的中频段主要动态环节为电压环和电流环；几百赫兹至2 kHz的高频段主要的动态环节为电流环、采样滤波器、控制延时和电压环.因此，在dq阻抗建模过程中，可在不同频段内考虑主要动态环节进行建模.

图3 展示了基于虚拟同步控制的港口岸电电源的宽频带小信号模型，港口岸电电源的输出电压与PCC 点电压之间存在稳态相位差δ0，因此港口岸电电源的输出电压转换为PCC 点电压时存在如下转换关系：

图3 港口岸电电源的宽频带dq小信号模型Fig.3 The broadband dq-frame small signal model of port shore power supply

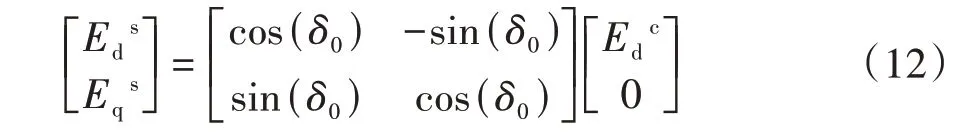
式中：δ0=P*/(3U0E0ωnLf)；U0是PCC 点的额定电压；E0是港口岸电电源输出端口的额定电压.

当港口岸电电源的端口注入dq轴的电压扰动时，其输出电压可表示为式（13）.

通过抵消式（13）中的稳态分量，并消除二次扰动分量可得dq轴向的电压扰动变化量.

由式（14）可得有功无功功率的小信号模型如式（15）所示.

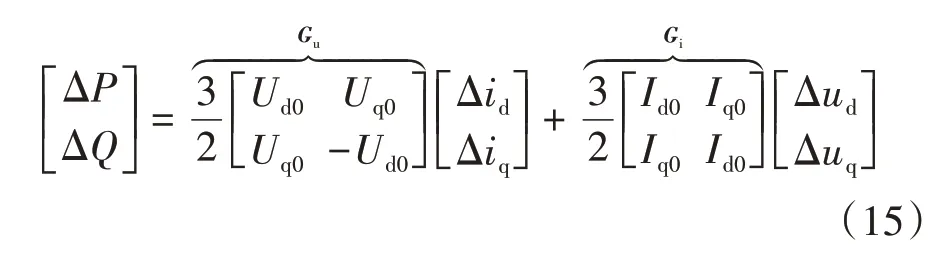
式中：Ud0和Uq0为PCC 点电压的dq分量；Id0和Iq0是输出电流的dq分量.

根据式（2）和式（3），有功和无功功率控制器的小信号模型表示如下：

根据控制器从αβ轴到dq轴的转变方式［24］，电流比例控制器及电压准比例谐振控制器的dq模型可推导如式（17）和式（18）所示.

在低频区域，控制延时和电压电流信号的低通滤波器等环节可忽略.此时，电流环可等效为“1”.港口岸电电源的dq模型可简化为图4所示.

图4 港口岸电电源在中频段的简化dq小信号模型Fig.4 The simplified dq-frame small signal model of port shore power supply in medium frequency band

根据图4，在低频区域，港口岸电电源的dq阻抗模型推导如下：

式中：Zc和Zl分别是滤波电容和电感的dq阻抗.

在中低频区域，控制延时和采样滤波器的dq模型可以忽略.此时，港口岸电电源的dq阻抗模型如式（20）所示.

在中频区域，考虑电压电流控制环，忽略功率环、采样滤波器和控制延时，港口岸电电源的δθ阻抗可推导如下：

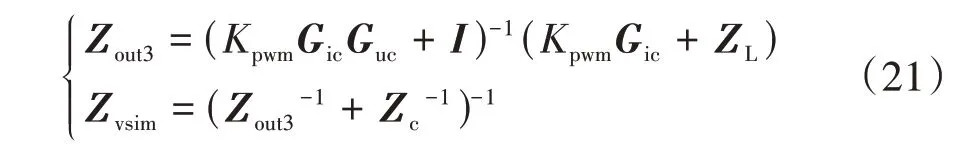
在高频区域，虚拟同步控制的港口岸电电源的功率控制环可以忽略，此时，其dq阻抗模型可推导如下：

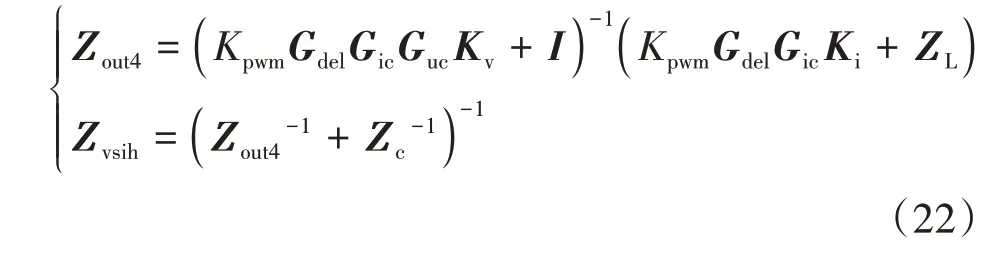
为验证本文所建分频段dq阻抗模型的准确性，基于图5 所示的硬件在环实验平台搭建了虚拟同步控制的港口岸电电源给PWM 整流器负荷供电的系统，其中虚拟同步控制和PWM 整流器的控制分别在两个TI DSP28335控制器中执行，控制器通过输入输出接口与RT_LAB 连接，系统主电路及扰动电流源由RT_LAB 仿真实现.表1 和表2 分别展示了港口岸电电源和PWM 整流器的控制及系统参数，采用并联注入理想电流源扰动的方式测量虚拟同步控制的港口岸电电源的dq阻抗.图6 展示了港口岸电电源的分频段阻抗模型和基于RT_LAB 实验平台的测量结果.由图6可知，尽管低频段模型与测量值有细微差异，港口岸电电源的分频段阻抗模型与测量值基本吻合，这证实了所建分频段dq阻抗模型的准确性.

图5 基于RT_LAB的实验系统平台Fig.5 Experimental system platform based on RT_LAB

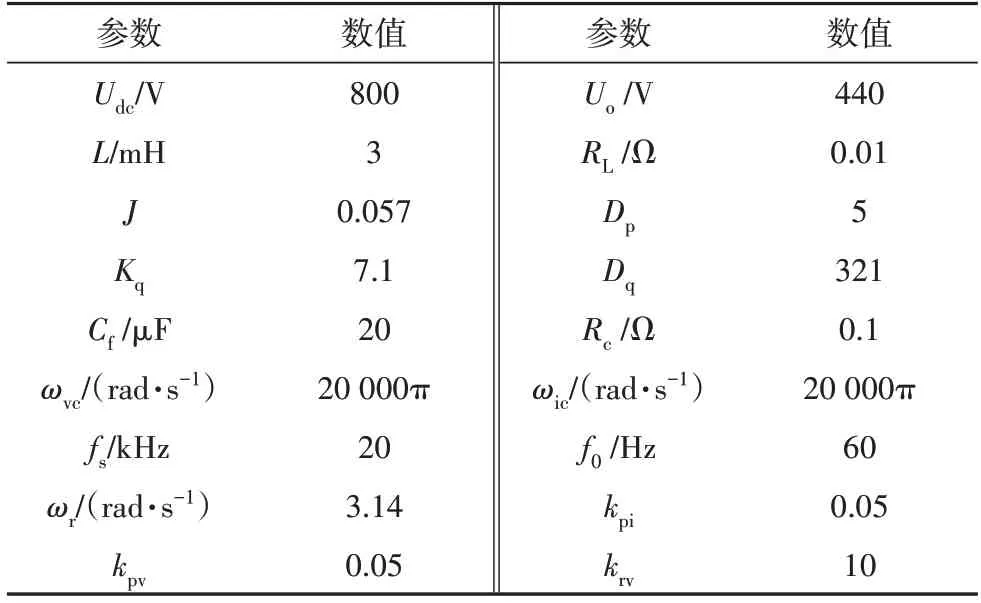
表1 港口岸电电源的控制及系统参数Tab.1 Control and system parameters of port shore power supply

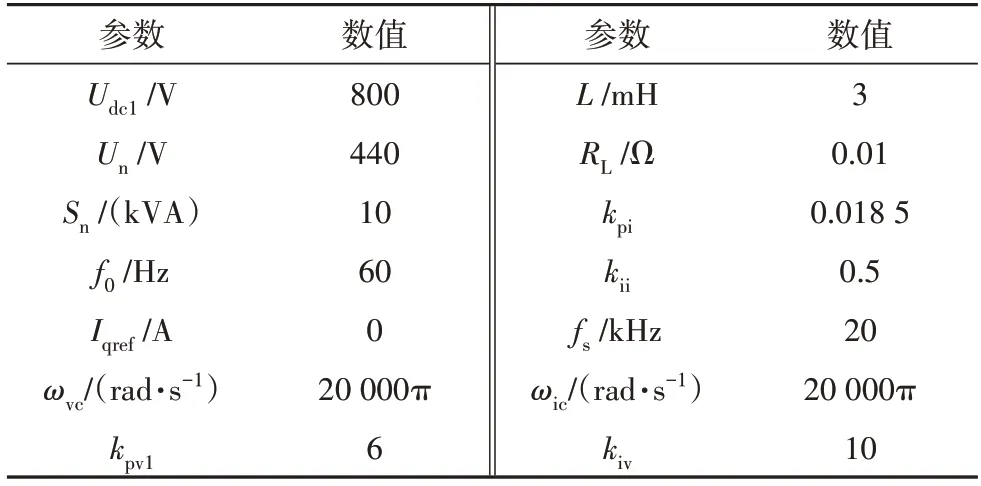
表2 船舶PWM整流器负荷的系统参数Tab.2 System parameters of ship PWM rectifier load

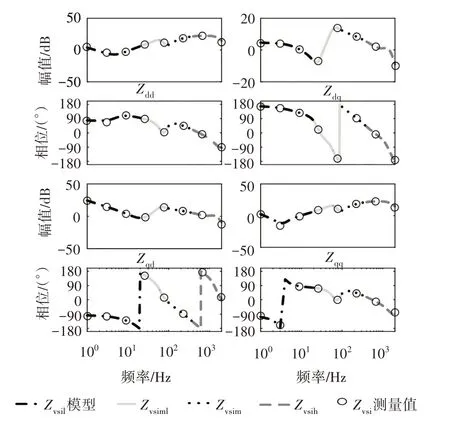
图6 港口岸电电源的分频段dq阻抗模型和测量验证Fig.6 Frequency division dq-frame impedance model and measurement verification of port shore power supply

3 港口岸电系统的稳定性分析

3.1 基于分频段dq阻抗模型的系统稳定性分析

受篇幅限制，本文不展示PWM 整流器的阻抗模型Zvsr，读者可参考文献［24］.由图7 可知，PWM 整流器的dq阻抗模型与仿真测量结果是吻合的.

图7 船舶PWM整流器负荷的dq阻抗模型和测量验证Fig.7 The dq-frame impedance model and measurement verification of ship PWM rectifier load

港口岸电电源和PWM 整流器负荷的dq轴耦合阻抗不可忽略.因此，GNC需应用于其阻抗比：

当且仅当Q（s）的特征根逆时针包围（-1，0）的次数等于Zvsi和Zvsr-1的右半平面极点个数时，系统才稳定.考虑到Zvsi和Zvsr-1不存在右半平面极点，当Q（s）特征根的奈奎斯特曲线不逆时针包含（-1，j0）时，系统是稳定的.而Q（s）的特征根的解如下：

3.2 港口岸电电源与船舶PWM 整流器负荷的控制相互作用分析

将式（19）～式（23）代入式（24），图8 展示了参数变化时，Zvsi/Zvsr的特征根.同时，为了验证系统的稳定性分析，在RT_LAB 中进行了实验验证.参数基于表1～表2，图9 显示了与图8 对应的系统交流接口电压的仿真波形.图8（a）显示了仅改变港口岸电电源的交流电压比例系数时，Zvsi/Zvsr的特征根的奈奎斯特曲线.随着港口岸电电源的kp_vsg的降低，λ1和λ2逐渐包围（-1，j0），这意味着减小港口岸电电源的电压比例系数，系统变得不稳定.图9（a）、（c）证明图8（a）分析的正确性，kp_vsg等于0.01，系统振荡；当仅增大kp_vsg为0.03 时，系统由不稳定变为稳定.图8（b）显示了仅改变港口岸电电源的电压谐振系数时，Zvsi/Zvsr的特征根的奈奎斯特曲线.随着kr_vsg的降低，λ1和λ2逐渐包围（-1，j0），这意味着减小港口岸电电源的电压谐振系数，系统同样变得不稳定.图9（a）、（d）证实了图8（b）分析的正确性.图8（c）显示仅改变船舶PWM 整流器负荷的直流侧电压比例系数时，Zvsi/Zvsr的特征根的奈奎斯特曲线.随着kr_vsr的增大，λ1和λ2逐渐包围（-1，j0），这意味着增大船舶PWM 整流器负荷的直流侧电压比例系数，系统变得不稳定.图9（a）、（b）证实了图8（c）分析的正确性.

图8 改变控制器参数时，Zvsi/Zvsr的特征根Fig.8 The characteristic roots of Zvsi/Zvsr when changing controller parameters

图9 改变控制器参数时，港口岸电电源的三相电压波形Fig.9 Three phase voltage waveform of port shore power supply when changing controller parameters

4 结论

本文采用dq阻抗分析法对虚拟同步控制的港口岸电系统进行了稳定性分析，得出以下结论：

1）根据虚拟同步控制的港口岸电电源的多时间尺度控制特性，本文提出了虚拟同步控制的港口岸电电源的分频段dq阻抗模型，并通过阻抗测量验证了模型的准确性.

2）船舶PWM 整流器负荷呈现负阻尼特性，虚拟同步控制的港口岸电电源的交流电压环与船舶PWM 整流器负荷的直流电压环之间的相互作用可能导致系统不稳定.增加港口岸电电源电压比例和谐振系数，或减小船舶PWM 整流器负荷的直流侧电压比例系数可增强系统的稳定性.