基于混合生成网络的软件系统异常状态评估

2022-05-06 06:06杨宏宇李译张良

湖南大学学报（自然科学版） 2022年4期

杨宏宇，李译，张良

（1.中国民航大学安全科学与工程学院，天津 300300；2.中国民航大学计算机科学与技术学院，天津 300300；3.亚利桑那大学信息学院，图森美国AZ 85721）

软件系统作为社会生产方式和信息化发展的成果之一，正朝着复杂化的方向不断发展，系统一旦产生异常［1］，将对软件系统的安全稳定运行造成影响［2］.为克服软件系统异常解决方案中存在的盲目性和被动性，需要对软件系统进行及时、有效的状态评估.软件系统异常状态评估是从异常的角度对系统状态进行评估，分析异常事件对系统造成的危害程度，为制定科学合理的软件系统安全保障方案提供客观依据和基础支持.

现有系统状态评估方法主要包括基于数学模型、基于逻辑规则推理和基于神经网络的方法［3-5］.基于数学模型的状态评估方法通过对影响系统正常运行的因素进行分析，建立影响系统运行因素与系统状态之间的对应关系.由于易受主观因素影响且实时性较差，基于数学模型的评估方法的评估结果不够理想，与实际情况偏差较大［6-7］.基于逻辑规则推理的状态评估方法根据先验知识构建模型并使用逻辑规则推理方法对系统状态进行评估，凭借先验知识对状态指标设置阈值判断系统状态，使得评估结果主观性强［8-9］.此外，由于软件系统运行过程中产生的状态信息量较大，基于逻辑规则推理的状态评估方法适应性较差.与基于数学模型和基于逻辑规则推理的状态评估方法相比，基于神经网络的状态评估方法由于具有高效和易拓展等特点应用更加广泛，该类方法利用训练数据集对特定模型进行训练后可以对系统状态进行分类，实现对系统状态的评估［10-12］，常用的方法包括AVE［13］、深度挖掘［14］、卷积神经网络［15］等.基于神经网络的状态评估方法虽然对系统状态的评估效果较好，但该类方法的通用性和可扩展性较差，对系统状态的量化分类效果不佳.

针对上述问题，本文提出一种基于混合生成网络的软件系统异常状态评估方法.首先，通过对长短期记忆网络（long short-term memory network，LSTM）和变分自动编码器（variational auto-encoder，VAE）的融合，设计一个LSTM-VAE 混合生成网络，以此为基础构建一种基于LSTM-VAE混合生成网络的系统异常状态检测模型.然后，采集系统关键特征参数数据，利用建立的LSTM-VAE异常状态检测模型对关键特征参数进行检测并获取其相应的异常度量值.最后，利用耦合度方法［16］对线性加权和方法进行优化，根据优化后得到的加权耦合度方法计算系统异常状态的量化值，实现对软件系统异常状态的量化评估.

1 软件系统异常状态评估方法

1.1 方法设计

基于混合生成网络的软件系统异常状态评估由基于长短期记忆网络-变分自动编码器（LSTMVAE）的系统异常状态检测模型（简称LSTM-VAE 异常检测模型）构建和系统异常状态评估两部分组成，如图1 所示.LSTM-VAE 异常检测模型构建为系统异常状态评估提供系统异常状态检测模型、异常阈值和最大重构误差；系统异常状态评估利用已构建完成的异常检测模型获取系统关键特征参数的异常度量值，然后通过加权耦合度方法对系统异常状态的量化值进行计算，根据系统异常状态的量化值实现软件系统异常状态评估.本文方法中两个部分的处理过程设计如下：

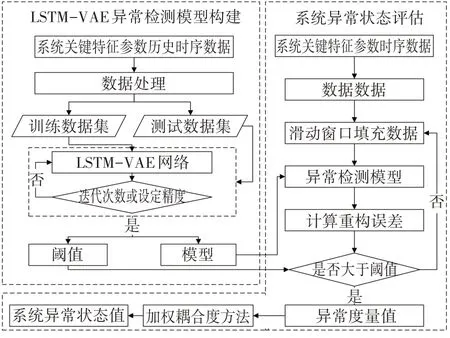
图1 软件系统异常状态评估方法Fig.1 Software system abnormal status evaluation method

1.1.1 基于LSTM-VAE 的系统异常状态检测模型构建

首先，筛选出系统正常运行时序的关键特征参数历史时序数据，输入LSTM-VAE 混合生成网络中进行训练，由训练完成后的LSTM-VAE 混合生成网络获取系统正常运行状态下的关键特征参数时序数据的长短期依赖关系和分布形式.

然后，将含有异常标注的关键特征参数的历史时序数据输入LSTM-VAE 混合生成网络中，获取系统关键特征参数的重构误差，此时的重构误差表示关键特征参数偏离正常状态数据的分布程度.

最后，利用标注的异常信息与模型检测结果统计模型准确率与召回率，选择准确率等于召回率时的阈值为异常阈值，选择重构误差中最大的数值为最大重构误差.其中，异常阈值为该关键特征参数偏离正常状态下数据分布程度的下限，用于判断系统关键特征参数是否异常，最大重构误差为关键特征参数偏离正常状态下数据分布程度的上限.

1.1.2 系统异常状态评估

首先，采集系统关键特征参数的时序数据，利用已构建的LSTM-VAE 异常检测模型对采集到的系统关键特征参数时序数据进行检测，获取系统各关键特征参数的异常度量值.

然后，依据AHP 的权重评定原则，采用1-9 标度法［17］确定系统各关键特征参数的相对重要度，对系统各关键特征参数进行权重赋值.

最后，利用加权耦合度方法计算系统异常状态的量化值，实现软件系统异常状态评估.

1.2 LSTM 与GRU的对比分析

目前，采用门控机制的神经网络模型主要包括长短期记忆网络（LSTM）和门控循环单元（gated re⁃current unit，GRU），LSTM 和GRU 的特点对比如表1所示.LSTM 和GRU 均是作为长、短期记忆的解决方案而提出的，两者都具有称为门的内部机制.不同之处在于：LSTM 具有3个门控单元，而GRU 相比LSTM少了一个门控单元，故从计算角度来看，GRU结构简单，效率更高.但是在数据集较大的情况下，与GRU相比，LSTM具有更强的表征能力［18］.

表1 LSTM 与GRU的比较Tab.1 Comparison of LSTM and GRU

本文的研究是在数据集较大的场景下开展的，故选择使用LSTM.虽然LSTM 牺牲了部分时间及计算的简便性，但LSTM对关键特征参数的表征能力更强也更灵活，对大数据环境的适应性更好.

2 基于混合生成网络的系统异常状态检测模型

2.1 变分自动编码器和长短期记忆网络

VAE 的基本结构如图2 所示.作为经典的无监督异常检测方法，VAE 在模型训练时无须大量标注数据，可通过辨识输入数据与重构输出数据间的差异来达到异常检测的目的.首先，由编码器对输入样本X=｛xk|k=1，2，…，n｝中的元素Xk进行拟合，使其服从均值为u和方差为σ的正态分布.然后，通过对所得正态分布进行采样得到隐变量Z=｛zk|k=1，2，…，n｝，其中，元素Zk服从均值为0 和方差为1 的标准正态分布.最后，由解码器对隐变量Z进行解码，生成输出样本Y=｛yk|k=1，2，…，n｝，通过计算X与Y之间的均方误差获得输入样本与输出样本之间的重构误差：

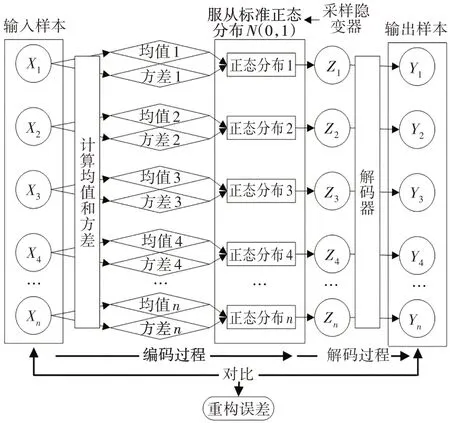
图2 VAE基本结构Fig.2 Structure of VAE

LSTM 通过记忆单元和门机制提取时序数据内部的长短期依赖关系，其神经元结构如图3 所示.LSTM 的遗忘门和输入门控制单元Ct的输入，输出门控制单元Ct的输出.其中，遗忘门和输入门分别控制上一时刻的状态Ct-1和当前时刻的状态输入记忆单元Ct中，输出门控制当前记忆单元Ct输入当前时刻的输出ht中.

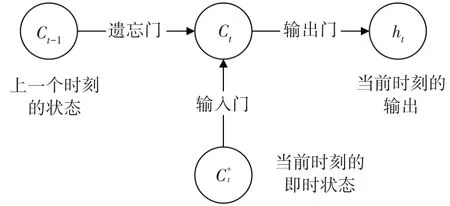
图3 LSTM神经元结构Fig.3 Structure of LSTM neurons

由上文分析可知，VAE和LSTM分别具有鲜明的特点，如表2 所示.VAE 的训练无须大量标注数据并且采样过程具有随机性，有助于提高模型的泛化能力.但是，VAE 对系统时序数据的时序特征不敏感，无法获取并表征系统时序数据内部的长短期依赖关系.由于系统关键特征参数数据具备明显的时序特征，LSTM 可以通过遗忘门、输入门和输出门控制记忆单元的状态，使其能够获取并表征系统时序数据内部的长短期依赖关系.

表2 VAE和LSTM 的特点Tab.2 Characteristic of VAE and LSTM

2.2 基于LSTM-VAE的混合生成网络设计

为解决现有异常检测方法在训练过程中需要大量标注数据和缺少对时序数据内部长短期依赖关系关注的问题，本文将LSTM 与VAE 融合，设计一个LSTM-VAE 网络（图4）.在该网络中，用LSTM神经元对VAE 的编码层和解码层中的神经元进行替换，即采用LSTM 对输入时序数据内部的长短期依赖关系进行提取，通过VAE 的变分推理对系统时序数据的分布进行建模.

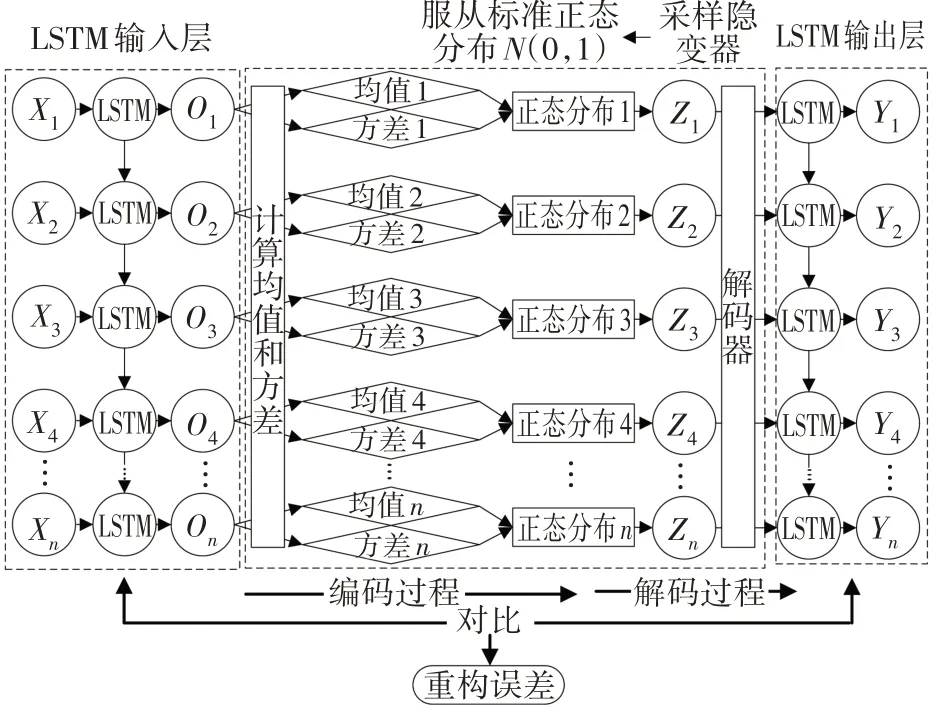
图4 LSTM-VAE网络结构Fig.4 Structure of LSTM-VAE network

与单一的LSTM 或VAE 相比，LSTM-VAE 网络可以对系统关键特征参数时序数据的长短期依赖关系进行提取，无须大量标注的关键特征参数数据训练模型，同时模型在隐变量学习过程中利用采样的随机性起到正则化作用，可以防止网络过拟合，使得LSTM-VAE 混合生成网络在提取时序数据特征和提高模型泛化能力方面更具优势.

2.3 基于混合生成网络的系统异常状态检测模型构建

以本文设计的LSTM-VAE 混合生成网络为基础，构建一个系统异常状态检测模型.该异常检测模型的构建步骤设计如下.

输入：系统关键特征参数的历史时序数据.

输出：异常检测模型.

步骤1：选取与系统状态相关的关键特征参数.

选择系统CPU 利用率、内存利用率、磁盘利用率和网卡吞吐率等特征参数作为系统状态异常检测和评估系统异常状态的关键特征参数，获取系统各关键特征参数的历史时序数据.

步骤2：系统关键特征参数预处理.

对系统关键特征参数进行归一化处理，抑制取值范围差异对训练产生的负面影响，

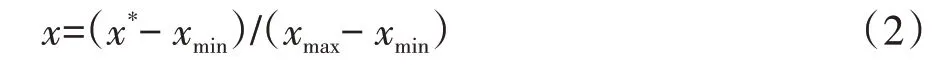
式中：x表示经过归一化之后的关键特征参数值，x*表示初始关键特征参数值，xmax表示关键特征参数中的最大值，xmin表示关键特征参数中的最小值.

步骤3：数据集划分.

将系统关键特征参数历史时序数据划分为训练集与测试集，训练集中不含异常标签的数据，测试集中含有异常标签的数据.

步骤4：模型训练.

利用训练集对LSTM-VAE 混合生成网络进行训练.采取滑动时间窗口法对关键特征参数的训练集序列进行子序列提取，假设时间窗口长度为l，关键特征参数序列长度为L，则可以从中提取L-l+1 个子序列.假设｛x1，x2，…，xl｝为系统CPU 利用率训练集中部分运行数据序列片段，其中，xi为i时刻系统CPU利用率，l为序列片段长度，LSTM-VAE 混合生成网络对｛x1，x2，…，xl｝进行网络重构后的输出序列为｛y1，y2，…，yl｝，采用均方根误差函数计算得到输入序列｛x1，x2，…，xl｝与重构输出序列｛y1，y2，…，yl｝之间的重构误差e

由混合生成网络输出的重构误差集合E为

式中：m=L-l+1，m为CPU 利用率训练集中数据序列片段个数，L为CPU 利用率训练集中数据序列长度，l为序列片段长度也即滑动时间窗口长度.

同样地，采用相同方法，得到系统的内存利用率、磁盘利用率和网卡吞吐率等关键特征参数的重构训练误差集合.当关键特征参数重构训练误差集合的所有重构误差均达到设定的精度要求或模型达到设定的迭代次数时，结束训练.

步骤5：异常阈值选择与最大重构误差.

将含有标签的系统各关键特征参数测试集输入已训练完成的LSTM-VAE 异常检测模型中.｛X1，X2，…，XL｝为系统CPU 利用率测试集中部分运行数据序列片段，其对应的标注信息序列片段为｛B1，B2，…，BL｝，其中，Xi为i时刻系统CPU 利用率数值，Bi为测试集中对应序列Xi的标注信息（Bi=1 表示i时刻该系统CPU 利用率数值异常，Bi=0 表示该时刻系统CPU利用率数值无异常），L为序列片段长度.

首先，将CPU 利用率测试集数据输入训练完成后的LSTM-VAE 异常检测模型中获取相应的重构输出序列，由公式（3）和公式（4）计算得到该关键特征参数测试集的重构误差集合Ecpu=｛e1，e2，…，em｝.

然后，定义CPU 利用率阈值ζ，将CPU 利用率测试集重构误差集合Ecpu中第i个数据序列片段的重构误差ei与CPU 利用率阈值ζ进行比较，若ei＜ζ，则表示异常检测模型判定该序列片段无异常，用Ci=0 表示；若ei≥ζ，则表示异常检测模型判定该序列片段异常，用Ci=1 表示.为评估模型性能，引入准确率和召回率指标.

准确率P：CPU利用率测试集中检测为异常的序列片段中标注为异常的序列片段的比例.

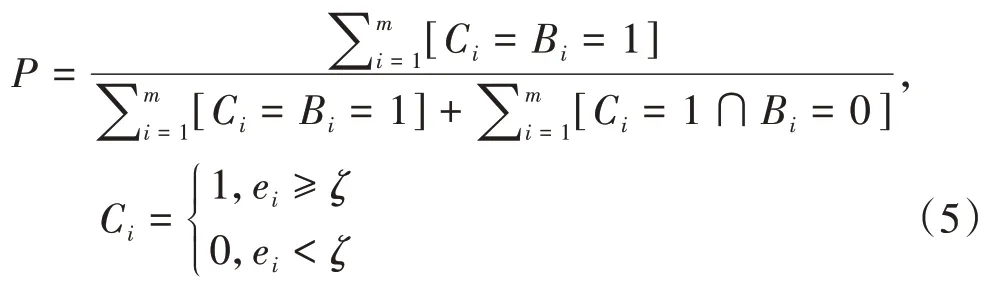
召回率R：CPU利用率测试集中标注为异常的序列中检测为异常的序列片段的比例.

最后，由准确率P和召回率R的定义可知，准确率P随阈值ζ的增大而增大，召回率R随阈值ζ增大而减小.当准确率P等于召回率R时，模型性能最佳.因此，定义此时的阈值ζ为CPU 利用率的异常阈值ζ*，其中，CPU 利用率的异常阈值ζ*表示该关键特征参数偏离正常状态下数据分布程度的下限.同时，定义该关键特征参数的最大重构误差ecpu为

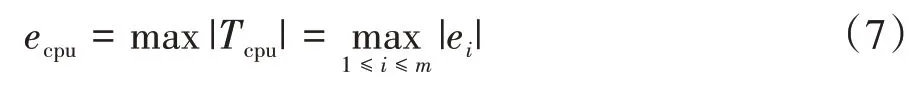
式中：ecpu为CPU 利用率的最大重构误差，表示该关键特征参数偏离正常状态下数据分布程度的上限.

同样地，采用相同方法，得到系统的内存利用率、磁盘利用率和网卡吞吐率等关键特征参数的异常阈值和最大重构误差.

3 系统异常状态评估

在完成LSTM-VAE 异常检测模型构建并获得系统各关键特征参数的异常阈值和最大重构误差后，将系统各关键特征参数的时序数据输入LSTM-VAE异常检测模型中，获取系统各关键特征参数的异常度量值.然后对系统各关键特征参数的权重进行赋值.最后利用耦合度方法对线性加权和方法进行优化，通过加权耦合度优化方法计算得到系统异常状态值.

系统异常状态评估部分的具体步骤设计如下：

输入：各关键特征参数的时序数据.

输出：系统异常状态值.

步骤1：获取各关键特征参数的异常度量值.

将系统关键特征参数时序数据输入LSTM-VAE异常检测模型中，计算输入序列与输出序列之间的重构误差.当重构误差小于异常阈值时，重新获取时序数据进行异常检测；否则，判断该关键特征参数为异常.然后，基于已获得的重构误差、异常阈值与最大重构误差，计算该关键特征参数的异常度量值

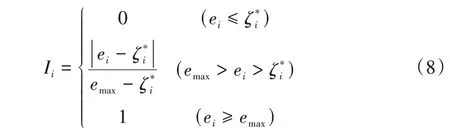
式中：Ii为系统第i个关键特征参数的异常度量值，ei为该关键特征参数此时的重构误差，为系统第i个关键特征参数的异常阈值，emax为系统第i个关键特征参数的最大重构误差.

步骤2：各关键特征参数权重赋值.

依据AHP 的权重评定原则，采用1-9 标度法确定系统各关键特征参数的相对重要度，构造决策矩阵M=（mij）n×n，决策矩阵M为

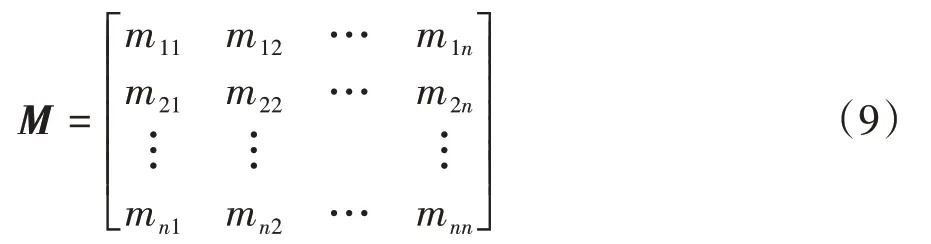
式中：n为系统关键特征参数的个数，元素mij表示第i个关键特征参数与第j个关键特征参数的重要程度之比，当i=j时，mij=1.

计算决策矩阵M的最大特征根λmax及其特征向量W=（w1，w2…，wn），

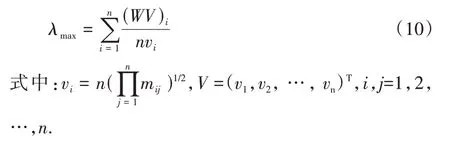
最大特征值λmax对应的特征向量W即为各关键特征参数的权重集合（w1，w2…，wn）.

步骤3：改进加权耦合度方法计算系统异常状态值.

线性加权和方法仅强调变量之间的独立性，不考虑变量间数值差异与相互作用问题，耦合度方法常用于表示变量间数值差异与相互作用.软件系统作为一个整体，其不同组件及关键特征参数之间的相互作用可能影响系统的正常运行.忽略不同组件及关键特征参数之间的差异和相互作用将导致系统状态评估时结果出现较大的差异.因此，本文在线性加权和方法的基础上融入耦合度方法计算系统异常状态值，即在量化系统异常状态时关注不同关键特征参数异常度量值间的差异给量化结果带来的影响.

首先，基于步骤1 获取的系统各关键特征参数的异常度量值Ii，计算系统耦合度H

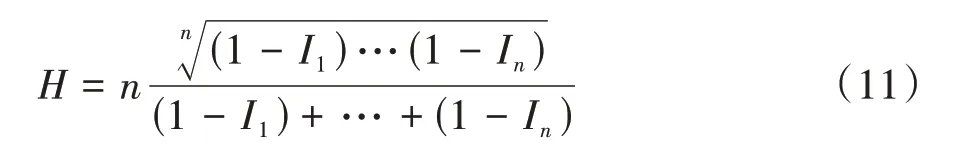
然后，利用系统各关键特征参数权重wi和系统各关键特征参数的异常度量值Ii，计算系统关键特征参数异常度量值的线性加权和S

最后，基于系统耦合度H和系统关键特征参数异常度量值的线性加权和S，计算系统异常状态值Sa

其中，系统耦合度H与系统关键特征参数异常度量值的线性加权和S的值均在［0，1］范围内.

根据指数函数的定义可知，式（13）在［0，1］范围内为单调递减函数，在S一定的条件下，H越小，则Sa越大；同样地，在H一定的条件下，S越大，则Sa越大.因此，根据该方法计算得到的系统异常状态量化结果符合本文的评估思路，即在计算系统异常状态值时关注不同特征参数的异常度量值之间的差异对评估结果造成的影响.

4 实验与结果分析

4.1 实验数据

实验数据集采用百度公司联合清华大学公开的运维数据集，选择其中的CPU 利用率、内存利用率、磁盘利用率与网卡吞吐率这四项关键特征参数进行异常检测验证实验.数据集中每个关键特征参数均包含连续4 周的数据，时间间隔为5 min.在实验中，将各关键特征参数的前三周数据划分为训练集，将最后一周数据划分为测试集，其中，训练集中数据均为系统正常运行时序数据且无异常数据，测试集中含有异常数据且异常数据已经标注.部分关键特征参数的数据格式如表3所示.

表3 关键特征参数数据格式Tab.3 Data formats for key feature parameters

4.2 LSTM-VAE混合生成网络配置及模型训练

LSTM-VAE混合生成网络由LSTM和VAE构成，输入向量维数等于输出向量维数，具体网络的配置如表4所示.

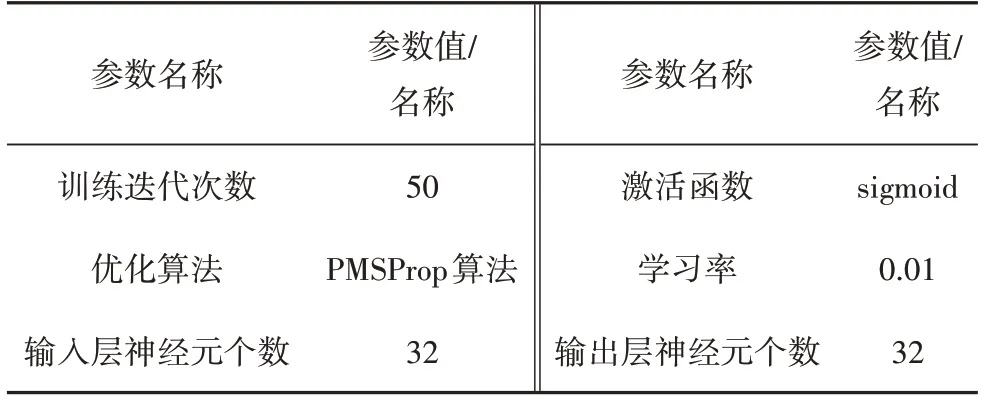
表4 LSTM-VAE网络配置Tab.4 Configuration of LSTM-VAE network

在训练过程中，各关键特征参数的训练误差与迭代次数关系如图5 所示.由图5 可见，各关键特征参数的训练误差随着迭代次数的增加而迅速减小.其中，各关键特征参数的误差曲线在经过35 次迭代后趋于平稳，表明模型达到较好的收敛效果，能够对系统正常的关键特征参数时序数据的长短期依赖关系和数据分布形式进行学习并实现数据重构.

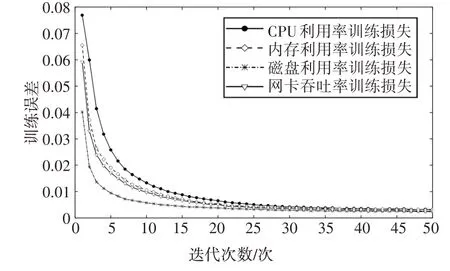
图5 训练误差与迭代次数Fig.5 Diagram of training error and number of iterations

4.3 异常阈值选择与评估效果

在实验中，通过遍历所有的可取阈值，确定异常阈值.可取阈值范围为0 到该关键特征参数的最大重构误差.设置初始阈值为0，若关键特征参数的重构误差大于0，将其视为异常；否则，首先计算阈值为0时的准确率和召回率，然后增加阈值并计算对应的准确率和召回率，当阈值设置为该关键特征参数的最大重构误差时结束.利用训练完成后的LSTMVAE 异常检测模型对系统各关键特征参数的测试集进行异常检测，得到相应的阈值与准确率、召回率的变化关系，如图6所示.

由图6 可见，当CPU 利用率的异常阈值为0.102时，CPU 利用率的准确率与召回率相等，因此选择CPU 利用率的异常阈值为0.102；当内存利用率的异常阈值为0.088时，内存利用率的准确率与召回率相等，因此选择内存利用率的异常阈值为0.088；当磁盘利用率的异常阈值为0.190时，磁盘利用率的准确率与召回率相等，因此选择磁盘利用率的异常阈值为0.190；当网卡吞吐率的异常阈值为0.122 时，网卡吞吐率的准确率与召回率相等，因此选择网卡吞吐率的异常阈值为0.122.

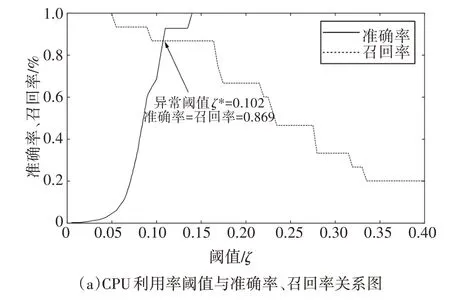
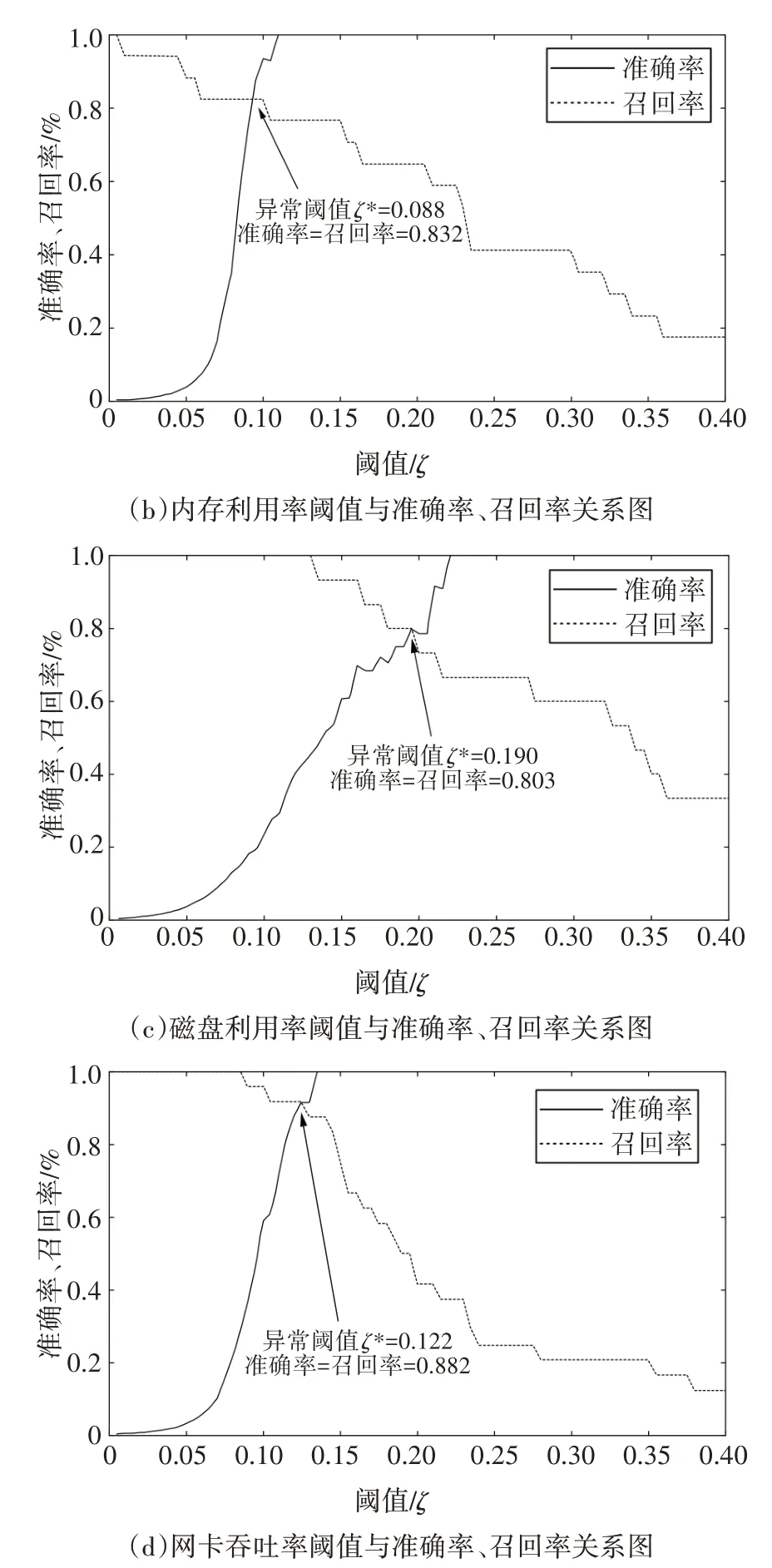
图6 各关键特征参数的阈值与准确率、召回率关系图Fig.6 Diagram of relationship between threshold values and accuracy rate，recall rate

基于系统各关键特征参数测试集，计算得到各关键特征参数对应的最大重构误差，结果如表5所示.

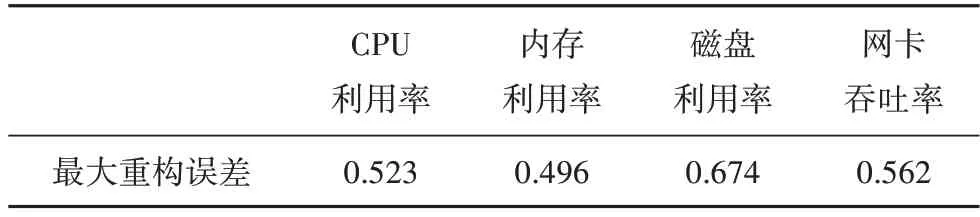
表5 各关键特征参数的最大重构误差Tab.5 Maximum reconstruction error of each key feature parameter

为评价本文异常检测模型的效果，分别采用VAE、AE、LSTM-AE 和LSTM-VAE 网络得到不同关键特征参数评估的F1-score 值，F1-score=（2×P×R）/（P+R）.各模型的F1-score值如表6所示.

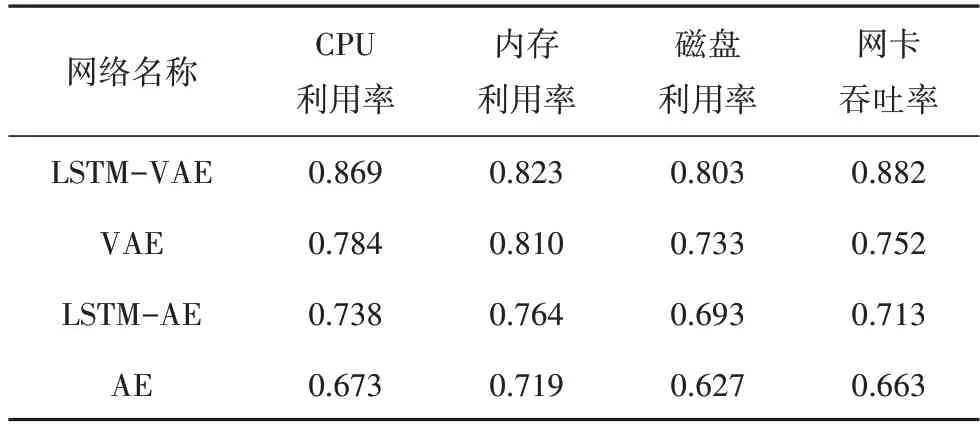
表6 不同网络在不同关键特征参数测试集中的F1-score值Tab.6 F1-score values of different models in different key feature parameter test sets

由表6 可见，针对测试集中的CPU 利用率、内存利用率、磁盘利用率和网卡吞吐率4 个关键特征参数测试数据，LSTM-VAE 网络模型的F1-score 值均优于其他模型.与VAE、AE 模型相比，LSTM-VAE 模型利用LSTM神经网络的时序特征提取能力，能够有效挖掘关键特征参数时序数据内部的长短期依赖关系，显著提升异常检测精度；同时，LSTM-VAE 网络可以利用VAE的隐变量空间，减少LSTM-AE网络中神经网络的过拟合对异常检测效果的影响，也有助于提升异常检测效果.

4.4 滑动时间窗口长度确定

由于滑动时间窗口长度L的取值会影响LSTMVAE 模型的异常检测效果，为了验证滑动时间窗口长度对LSTM-VAE 模型的异常检测效果的影响并确定最佳的滑动时间窗口长度值，有必要进行滑动时间窗口长度影响实验.

在实验中，选取不同窗口长度L的值并计算其对应的F1-score 值，选择窗口长度值从长度4 到20依次增加2个单位长度进行实验.选择最高F1-score值所对应的窗口长度作为LSTM-VAE 模型的滑动时间窗口长度L的值，不同滑动时间窗口长度L与对应的F1-score值如图7所示.

由图7 可见，当滑动时间窗口长度L为12 时，LSTM-VAE 模型对各关键特征参数测试数据的F1-score 值均大于其他滑动时间窗口长度对应的F1-score 值，表明滑动时间窗口长度为12 时，LSTMVAE 模型对系统状态的异常检测效果最佳，所以，在LSTM-VAE 模型中，将滑动时间窗口长度L的值设定为12.

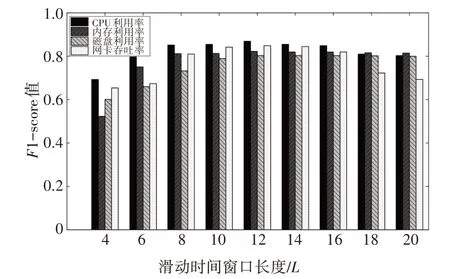
图7 滑动时间窗口长度与F1-score值Fig.7 Sliding time window lengths and the corresponding F1-score values

4.5 异常状态评估

4.5.1 关键特征参数异常度量值与关键特征参数赋权

在确定系统各关键特征参数的异常阈值和最大重构误差后，为保证实验结果具有可比性，选取10组关键特征参数异常时序数据组成测试集，用本文模型的方法对该数据集进行检测并计算关键特征参数的重构误差，由公式（7）计算测试集中关键特征参数的异常度量值，由公式（11）计算各测试集的系统耦合度，测试集中各关键特征参数的异常度量值如图8 所示，测试集中各关键特征参数的系统耦合度如图9所示.

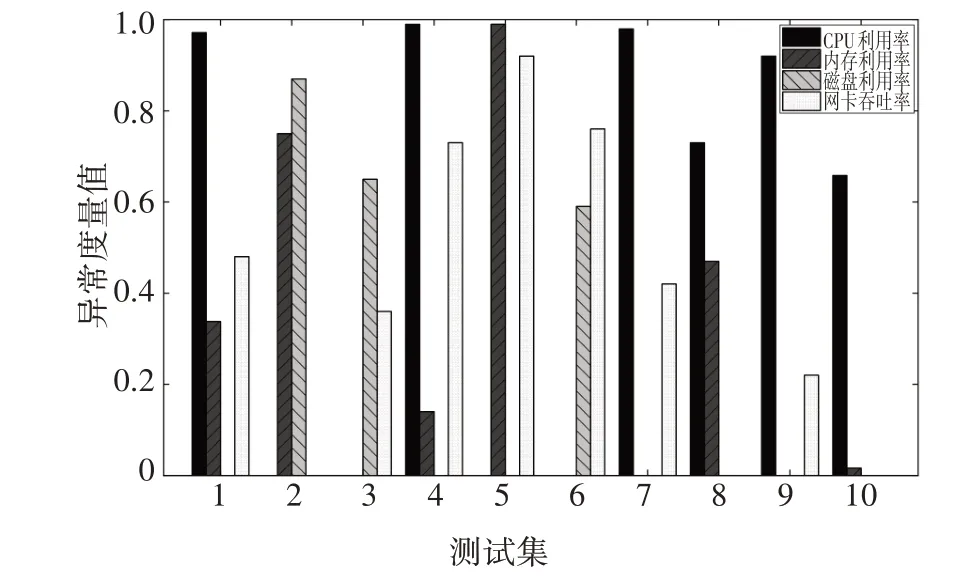
图8 测试集中各关键特征参数的异常度量值Fig.8 Key feature parameters anomaly metric value in the test group

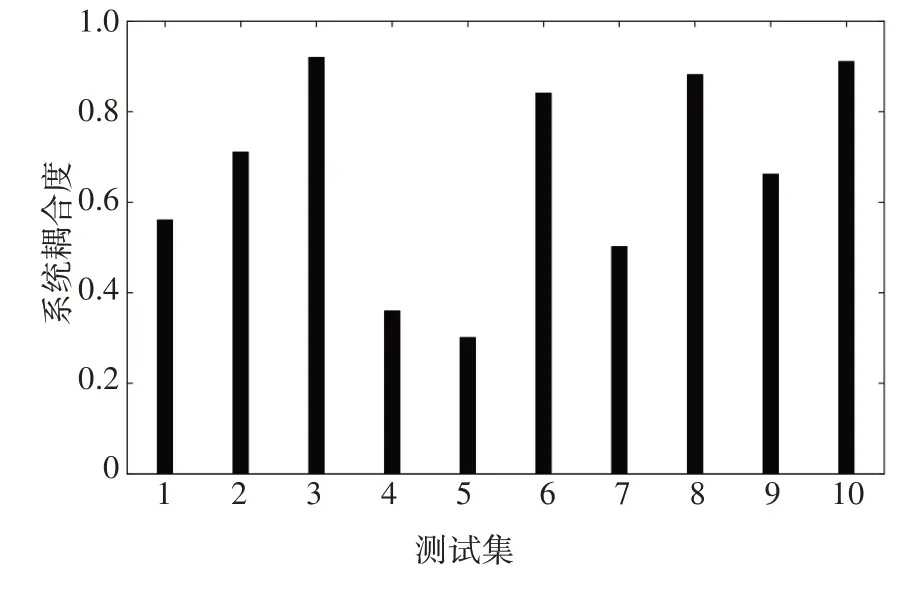
图9 各测试集的系统耦合度Fig.9 System coupling degree of each test group

采用加权耦合度方法计算系统异常状态值时，需要对系统各关键特征参数进行赋权.利用AHP 方法对系统关键特征参数进行主观赋权，根据AHP 权重评定原则，采用1-9 标度法确定系统各关键特征参数的相对重要度，建立决策矩阵如表7所示.

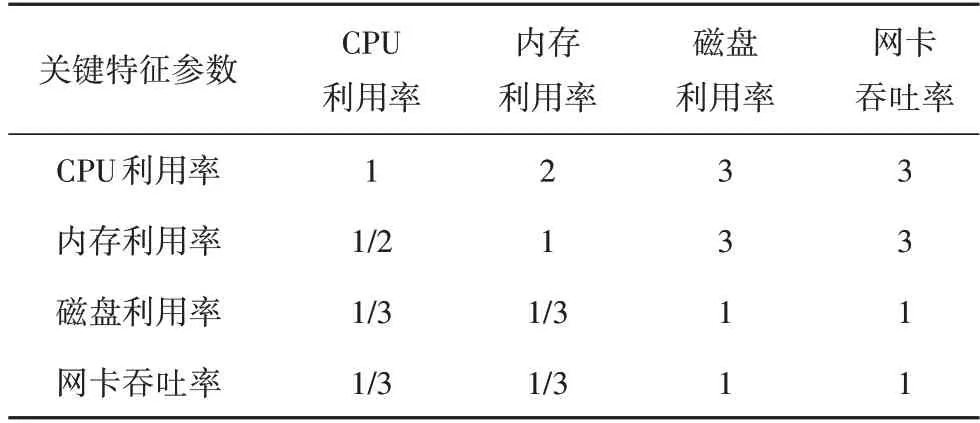
表7 决策矩阵Tab.7 Decision matrix

计算得到决策矩阵的最大特征根及其对应的特征向量，如表8所示.

表8 最大特征值及其特征向量Tab.8 Maximum eigenvalue and its eigenvector

由表8 可见，CPU 利用率权重为0.443 5，内存利用率权重为0.312 1，磁盘利用率权重为0.122 2，网卡吞吐率权重为0.122 2.

4.5.2 系统异常状态评估

由4.5.1 节的实验过程得到测试集中各关键特征参数的异常度量值、各测试集的系统耦合度和相应的关键特征参数权重，由公式（13）计算各测试集的系统关键特征参数异常状态值.在系统异常状态评估阶段，使用线性加权和方法、TOPSIS 方法和本文方法计算得到系统的异常状态结果，如图10所示.

由图10 可见，在测试集4、5 和7 中，与线性加权和方法和TOPSIS 方法得到的异常状态值相比，本文方法得到的异常状态值差异较为明显.同时由图8可见，在测试集4、5 和7 中，多个特征参数的异常度量值较高，且不同特征参数的异常度量值之间差异较大.同时由图9 可见，与其他测试集的系统耦合度值相比，测试集4、5 和7 的系统耦合度值较小，在系统特征参数异常度量值的线性加权和一定的条件下，耦合度值越小的测试集，其系统异常状态值越大.因此，与其他方法计算得到的异常状态值相比，本文方法计算得到的测试集4、5 和7 的异常状态值差异较为明显.

图10 实验结果对比图Fig.10 Comparison of experimental results

同样地，在测试集3、6和10中，与线性加权和方法和TOPSIS 方法得到的异常状态值相比，本文方法得到的异常状态值差异较小.同时由图8 可见，在测试集3、6 和10 中，其总体特征参数的异常度量值较低，且不同特征参数的异常度量值之间差异较小.同时由图9 可见，与其他测试集的系统耦合度值相比，测试集3、6 和10 的系统耦合度值较大，在系统特征参数异常度量值的线性加权和一定的条件下，耦合度越大的测试集，其系统异常状态值越接近特征参数异常度量值的线性加权和.因此，与其他方法计算得到的异常状态值相比，本文方法计算得到的测试集3、6和10的异常状态值差异较小.

上述结果的原因在于，本文方法在计算系统异常状态值时考虑了系统耦合度因素.由于耦合度能够反映系统各关键特征参数异常度量值间的差异，但不能反映系统异常状态值大小，因此本文方法在计算系统异常状态值时，在线性加权和的基础上融入耦合度因素，即在计算系统异常状态值时能够关注不同关键特征参数异常度量值之间的差异，故本文方法得到的结果更为合理.

5 结论

针对现有软件系统异常状态评估方法过度依赖数据标注、对时序数据的时间依赖性关注较低和系统异常状态难以量化等问题，本文提出一种基于混合生成网络的软件系统异常状态评估方法.首先，针对异常检测方法过度依赖数据标注和对时序数据的时间依赖性关注较低等问题，设计一种基于LSTMVAE 混合生成网络的异常检测模型，解决异常检测模型应用场景受限和准确率较低的问题.然后，利用LSTM-VAE 异常检测模型对系统关键特征参数进行检测并对其异常度量值进行计算，为后续系统异常状态评估提供可靠的数据支撑.最后，通过加权耦合度优化方法计算系统异常状态值，解决传统软件系统状态评估方法难以对系统异常状态进行量化的问题.实验结果表明，本文方法对系统异常时序数据的时间特征更为敏感，评估结果也更为合理、有效.

由于本文在系统关键特征参数权重赋值过程中存在一定的主观因素，可能导致软件系统异常状态的评估结果随评估主体的不同而改变，下一步将重点研究采用主客观相互结合［19］的赋权方法以减少主观因素对软件系统异常状态评估的影响.