始于举例 走向推理——《和的奇偶性》教学设计

文|陈志睿

【教学内容】

苏教版五年级下册第50、51页。

【教学过程】

一、猜想：基于经验，推测结论

1．猜想两个自然数相加和的奇偶性。

课前布置如下研究任务：

2.猜想多个自然数相加和的奇偶性。

课前布置如下学习任务：

二、验证：始于举例，走向推理

1．验证两个自然数相加和的奇偶性。

师：一定会有同学对课题有疑问，什么是和的奇偶性呢？谁来说说？

（学生各抒己见）

师：是的，自然数相加，和什么时候是奇数，什么时候是偶数，是有规律的，而这个性就是规律的意思。我已经在大家的发言里听到了一些这样的规律，谁再来具体说一说？

（板书：偶数+偶数=偶数

偶数+奇数=奇数

奇数+奇数=偶数）

师：这三个结论我们还没有经过验证，目前还是一个猜想，可能是对的，也可能是错的，我们这节课的重点就放在验证上。

师：进行6分钟讨论，还没有完成的同学，如果有人给了你启发，请及时记录想法。完成好的同学，在举例验证的基础上，尝试画图、推理验证。

（1）举例验证。

师：你是怎样验证“偶数+偶数=偶数”的？

预设：都是一些很简单的例子：2+2=4，2+6=8，4+6=10。

师：同学们仔细观察这三个例子，其实它们是同一类型的例子。（分别指一指两个加数）你们发现了吗？

预设：都是一位数加一位数的。

师：在举例验证的时候要尽量把例子考虑得全面一点，你还能找一个与这个不同类型的例子吗？

预设：一位数加两位数的，8+12=20，20是偶数。

预设：24+238=262，262也是偶数。

师：还可以考虑一些数位更多的数或者特殊的例子吗？

预设：1576+578，3900+740……

（2）推理验证。

师：1576+578和3900+740这两个算式里的数这么大，你是通过计算出结果验证它们的和是偶数的吗？还有什么别的方法？

预设：我不用计算就知道，只要看它们的个位，6+8等于12，和的个位是2，我们知道个位是0、2、4、6、8的数就是偶数，因此和就是偶数。

师：看来用只加个位的方法就能帮助我们快速判断。

出示PPT：

师：这么多例子能举得完吗？会不会出现一个反例，两个偶数相加的和却不是一个偶数？同桌之间商量一下。

预设1：不会有反例的，偶数的个位是0、2、4、6、8，因为它们相加的结果个位还是偶数，所以和是偶数。

预设2：我们之前学过，偶数都是2的倍数，因为2的倍数加2的倍数和仍然是2的倍数，所以和是偶数。

（根据学生的回答相机出示PPT。再验证“偶数+奇数=奇数，奇数+奇数=偶数”，学生自然地想到从个位思考）

总结：在举例的基础上，我们根据偶数、奇数的特点，只要考虑个位相加的情况，和的个位是偶数就是偶数，和的个位是奇数就是奇数。就把所有的可能性都考虑到了，同学们，这就是推理。

（3）图形验证。

师：还有哪些同学用图形验证的呢？

学生用画图验证“奇数＋奇数”。

预设：单独的两个圆又可以组成一对，所以结果是偶数。

师：仔细观察这些图，结合刚刚有同学提到一双一双的筷子就是偶数，一双筷子加一支就是奇数，所以你们认为什么样的图形可以代表奇数，什么样的图形可以代表偶数？

明确：偶数除以2没有余数，因此总是两个一对的、没有落单就是偶数；奇数除以2会余1，余数1就是那个落单的，把奇数想成那一个落单的即可。

出示PPT：

偶数÷2 没有余数

奇数÷2 余1

总结：偶数和偶数在一起永远都没有落单，偶数+奇数会有一个落单，结果就是奇数。奇数和奇数两个落单的可以配对。这样我们就把数转化成形，通过图形去说理，特别有说服力。

2．验证多个自然数相加和的奇偶性。

师：多个自然数（0除外）相加，什么情况下和是奇数，什么情况下和是偶数？请大家在四人小组里讨论。小小提醒，可以利用上面三个结论帮助思考，当然如果刚才讨论的画图法、推理法对你有启发，也可以和同学们分享。

判断1：多个偶数相加，和一定是偶数。

预设1：这句话是对的，因为我们已经知道了“偶数+偶数=偶数”，那么再多的偶数相加仍然是偶数。

预设2：刚刚我们知道了偶数的图形就是两个两个配对的，那么不管多少个偶数相加，都不会有一个落单的，所以多个偶数相加，结果仍然是偶数。

判断2：多个奇数相加，和一定是奇数。

预设：这句话是错的。举一些例子：1+1+1+1=4，1+1+1+1+1=5，3+5+7+9=24，3+5+7+9+11=35。和有时候是奇数，有时候是偶数。

师：你举的例子虽然简单，但确实说明了这句话是错的，那到底什么情况和是奇数，什么情况和是偶数呢？

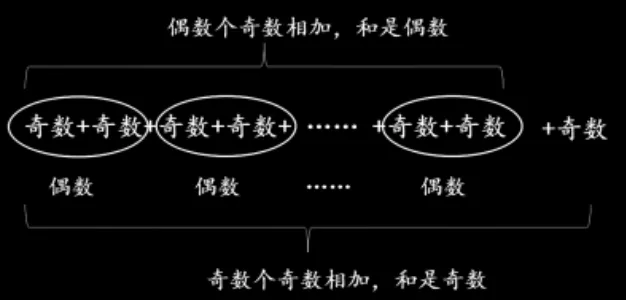
预设：有奇数个奇数相加的时候，和是奇数；偶数个奇数相加的时候，和是偶数。

师：我们来验证大家的发现。同学们写的这么多式子，我用一道式子就能表示出来，猜猜看是什么样的式子？

呈现：

三、回顾反思：提炼方法，巩固提高

师：回顾刚刚的探究过程，你有哪些收获？

预设：一开始只会举例，但是上完这节课我知道可以用画图和推理的方法去验证结论。