利用教材题组发展学生数学思维的实践与反思

文|戴梦竹

题组设计是浙教版《数学》教材的重要特色之一。好的题组能有效帮助学生在学习新知时降低探究难度，在应用概念时避免机械操练，感受自主创造、自觉内化的乐趣，促进数学思维和数学情感的积极发展。

以下尝试对教材中的题组编写策略进行一定的整理和反思，以方便一线教师共同读懂、用好，乃至借鉴创编相应的练习。

一、一题多变设计题组

一题多变是最常见的题组形式，为了凸显知识的本质，培养学生分析、综合、抽象、概括的能力，教材设计了大量变式练习调动学生思维。

（一）改变叙述方式，强化抽象与概括。

1.情境变化型。

一些学生在解决问题时，常常被题目的情境所迷惑，不能识别出问题的根本模型。针对学生只会解一道题，而不是一类题的情况，可有意识地以题组形式呈现情境变化的问题。如，在学习工程问题时，我们进一步改编浙教版《数学》五年级下册第76页练习数据，构造题组——

（1）一条道路，甲队单独修12天能完成，乙队单独修18天才能完成，如果两队合修，多少天能修完？

（2）甲车从A地开到B地需要12分钟，乙车从B地开到A地需要18分钟，两车同时从两地相向开出，经过几分钟相遇？

（3）一笔钱单独买衣服可以买12件，单独买裤子可以买18条，如果一件衣服和一条裤子配成一套，这笔钱最多可以买几套？

引导学生在具体练习的基础上，建立不同情境之间的对应，感悟相同的数量结构。

2.表达变化型。

通过不同的叙述方式呈现题目中的某个条件，有利于学生对不同的数学概念、公式、工具进行链接。如——

（1）西山苗圃中松树苗占地2.7公顷，比柏树苗的占地面积多。柏树苗占地多少公顷？

（2）西山苗圃中松树苗占地2.7公顷，柏树苗的占地面积比松树苗少。柏树苗占地多少公顷？

（选自浙教版《数学》六年级上册第41页）

学生通过对两题的关系句进行分析，发现不同的表述方式反映出相同的数量关系，即松树苗占地面积是9份，柏树苗占地面积有这样的8份，数量关系式都可以写成：松树苗占地面积×=柏树苗占地面积。放手让学生继续改编题组，学生还会联想到倍、比等知识，这样在不知不觉中对知识进行了扩展和串联。

3.问题变化型。

利用相同信息发展出不同的问题，使一道题目变成一组题目，有助于培养学生思维的灵活性。如，在学习四则运算应用问题时，原教材配有题组——

某食品厂计划18天生产饮料540箱，实际前4天生产144箱。照这样计算：

（1）可以提前多少天完成？

（2）18天可以多生产多少箱？

（3）剩下的还要生产多少箱？

（4）剩下的时间还可以生产多少箱？

（5）生产12天后，还剩多少箱没完成？

（选自浙教版《数学》四年级上册第79页）

根据信息，这道题中有两个归一量，即“计划每天生产箱数”和“实际每天生产箱数”，学生需要根据问题，灵活选择信息，找准归一量进行解题。这样的题组练习对学生整体把握和辨析数量关系提出了更高的要求。

（二）增加推理层次，强化分析与综合。

1.隐藏信息型。

数学学习中，在学生掌握了基本的概念和结构以后，不妨将题目中的一些直接信息变为间接信息，为学生提供“化归”的学习机会。例如——

（1）有5盒同样的玻璃球，每盒的个数一样。如果各取出12个，取出的个数正好是原来2盒玻璃球的个数。原来每盒有多少个玻璃球？

（2）5只桶里的水一样多，如果从每只桶里倒出6千克水，5只桶里剩下的水相当于原来2只桶里的水。原来每只桶里有多少千克水？

（选自浙教版《数学》四年级上册第83页）

第（1）题是第（2）题的基础，第一题取出个数对应的盒数已知，利用取出个数除以对应盒数就能解题。第二题将倒出质量对应的桶数隐藏起来，学生解题时要先将“剩下的水相当于原来2只桶里的水”转化成“倒出的水相当于原来3只桶里的水”，增加了推理层次，丰富了化归的体验，突出了“对应”的思想。

2.综合运用型。

在练习过程中，教师如果仅呈现知识点比较单一的问题，学生会依靠思维惯性，不假思索地写出答案，失去了锻炼思维的价值。而随着学习的推进，把同一领域不同方面的知识，不同领域的知识，乃至不同学科的知识，不断整合、迭代，则可帮助学生不断升级自己的知识结构和能力水平。如下面这组题——

（1）如图所示，这个物体的体积是多少立方分米？

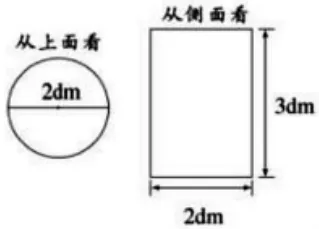
（2）一个立方体钢坯的棱长是0.5m，把它锻造成横截面面积是10dm2的长方体钢材。锻造成的钢材有多长？（用方程解答）

（3）一个圆锥形的容器高15cm，底面直径是8cm，容器装满水后，将水倒入底面直径为16cm、高为15cm的圆柱形容器中。水面距圆柱形容器上端多高？

（选自浙教版《数学》六年级下册第71、72页）

这样的题组，从易到难，既考查了圆柱体积的知识，又考查了立方体体积、圆锥体积、体积单位、方程等知识。在练习过程中，学生需要辨析概念之间的差别和联系，对空间想象能力的要求不断攀高，思维得到了锻炼。

二、利用对比设计题组

为了打破思维定势，教材通过将顺向思维的题目逆向化或将本节课的内容与前面所学内容进行比较等方式设计一批对比题组，使学习效果事半功倍。

1.正逆对比型。

很多所谓的基本问题，都是顺着情境发生发展就可以顺理成章得到答案的问题。这时，只要把情境事实稍微加以符号化就可以了。而只有当学生对于逆向问题也能够头头是道地展开分析，我们才认为他的头脑中具备了相应的数学结构，使得他们可以超越具体情境的限制，基于数学关系，进行多向度的推导。

例如，将“相遇问题”中的条件和问题进行轮换，帮助学生从整体上把握速度、时间和路程之间的关系。

（1）货车和客车分别以60千米/时和80千米/时的速度行驶。它们同时从A、B两城市出发，相向而行，3小时后相遇。A、B两城市相距多少千米？

（2）货车和客车同时从相距420千米的A、B两城市出发，相向而行，速度分别是60千米/时和80千米/时。几小时后相遇？

（3）货车和客车同时从相距420千米的A、B两城市出发，相向而行，3小时后相遇。货车的速度是60千米/时，客车的速度是多少？

（选自浙教版《数学》四年级上册第24页）

2.相似对比型。

数学学习过程中，还经常会发生将新知识与之前学过的相似知识混淆，用同种思维去解决性质不同的题目的错误。将涉及相似知识点的题目组织起来，进行对比分析，可以帮助学生做好基本概念的强化和分化。如，学习正比例和反比例后，提供题组——

（1）浓度一定，水和药的用量成（ ）比例。

（2）长方体的体积一定，长方体的底面积和（ ）成反比例。

（3）ab=c，当a一定时，b和c成（ ）比例；当c一定时，a和b成（ ）比例。（a、b、c均不等于0）

（选自浙教版《数学》六年级下册第38页）

通过对正比例、反比例的辨析，学生容易发现正比例和反比例的区别与联系，掌握概念的本质。如果进一步让学生对正比例和反比例进行相互的转化与改编，学生在应用过程中，还能概括出：凡是成分总关系的一组数量，必定存在着正、反比例的关系。

三、利用开放因素设计题组

数学教学应体现开放性，倡导学生多视角看问题，拓展他们思考和创新的空间。教材在问题的提出和解答方式上挖掘开放因素，给学生留有充分的自由度。

1.开放条件或问题。

学生不但应具备解决问题的能力，更应具备创造性提出问题和改编问题的能力，后者对学生的思维要求更高。设计条件或问题不唯一的题组，让学生在不断尝试中增进思维的发散性和系统性。例如——

先把下列各题的条件补充完整，再计算。

（1）白兔有34只，________。白兔和黑兔一共有多少只？

（2）李师傅修理了34把椅子，____________。张师傅修理了多少把椅子？

（3）书架上原来有25本书，____________。现在有多少本？

（选自浙教版《数学》二年级上册第53页）

由于学生思维层次不同，对数量关系的理解水平存在差异，他们编的题目有难有易。实际教学时，通过小组讨论和全班交流，大家可以相互借鉴，既生成共同概括，又体验不同变化，每个人都能在自己原有思维水平的基础上有所突破。

2.开放解题结果型。

结果不唯一的练习除了要求学生能解题外，还要求学生积极考虑存在的其他可能性，甚至所有的可能性，不断挖掘学生潜力。如，浙教版在《除数是两位数的除法》单元中配有如下练习——

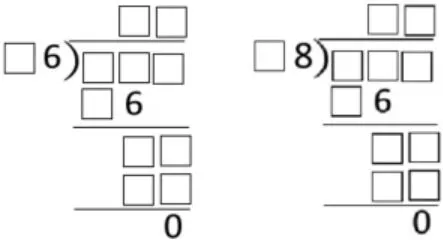
（选自浙教版《数学》四年级上册第29页）

像这样的开放设计，学生为探究不同结果，会主动去尝试大量的计算，而在尝试的基础上，逐渐生成反思和归纳，巧妙应用有序思考，理性分析所有可能。从普遍的尝试——检验策略自主过渡到更高思维层次的组合——推理策略，体现了创新思维的发展。

题组练习是创建小学数学整体教学、差异发展的有效途径。教师在教学中，自觉运用上述策略，不仅能增强数学教学的趣味性，更能为学生建构良好的数学知识结构，发展思维的深刻性与灵活性提供机会。