基于行波理论的配电线路漏电点检测与定位

涂志威

（国网电力科学研究院武汉南瑞有限责任公司，湖北武汉 430074）

配电线路能够很好地承载电压，实现电力能源输送。配电线路在传输电能的过程中会受到外界环境、介质的干扰，加速线路老化的速度。如果干扰程度较大，经过一段时间配电线路就会出现局部漏电的现象，从而影响输配电工作的稳定性。而及时对配电线路漏电点进行检测是保证配电线路持续工作的有效方法[1-2]。

就目前配电线路的发展情况来看，配电线路主要分为单行电子线路和多行电子线路。传统的配电线路漏电点检测与定位方法应用于单行电子线路中时可以达到应用标准，但是对于多行电子线路漏电点的检测与定位的误差偏大，从而影响线路漏电点的最佳维修时间，易造成严重的电力事故。

为了解决以上问题，该文提出了基于行波理论的配电线路漏电点检测与定位方法。

1 配电线路漏电点检测

行波理论中认为：当波的振动作用于卵圆窗时，基底膜会随之产生振动。振动的幅度会随着波的推进而逐渐增加。当波运动到基底膜的某一位置时，振幅可达到最大。在这之后，振动停止并消失。

行波理论表示，所有的声音、信号在基底膜的传输下都具有独特、唯一的振动频率，反之根据基底膜反馈的振动频率，可以完成相应事物状态的检测[3-4]。行波理论传播的折反图如图1 所示。

图1 行波理论传播的折反图

因此，将行波理论运用于电力领域，可以认为，行波理论概述了信号波和振动频率之间的关系。对于该文设计的配电线路漏电点的检测方法来说，配电线路正常运行时不会产生外部电流，一旦线路出现漏电现象，会引起线路周边的电磁场发生变化，而其反馈的振动频率也会随之出现波动，由此可以判断配电线路的漏电状态[5-6]。

对于正常工作的配电线路，线路振荡波所放电的脉冲波根据线路承载电压的大小，在一定数值上下进行波动，一旦脉冲波动值出现大幅度的降低和升高，代表线路出现内部冲突，此冲突会导致配电线路的漏电。经过研究分析，具体的配电线路振荡脉冲放电波的波动特征如下：

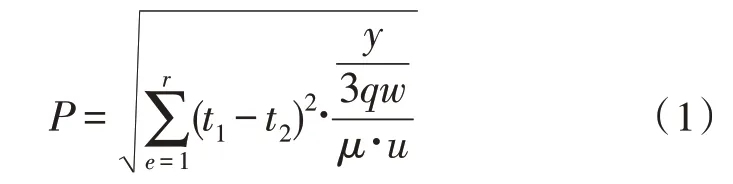
其中，q表示基础波形与脉冲峰值；t1表示线路振荡波所放电的脉冲上升时间；t2表示线路振荡波所放电的脉冲下降时间；r、e分别代表特征处理的上、下限物理积分数值；y代表脉冲时间内远距跨越电缆放电波形的总形变量，μ表示振荡波的平均放电系数，u表示电缆线路中振荡波的传输幅值[7]。

配电线路内部每帧振动脉冲都对应一个振动等效频率，根据两个变量之间的关系，可以准确地确定配电线路各个测试点的行波波动情况。如果两个变量相对参数匹配错误，那么所计算配电线路的行波振动频率值就是异常的[8-9]。线路振荡所放电的脉冲波的等效频率计算公式如下：

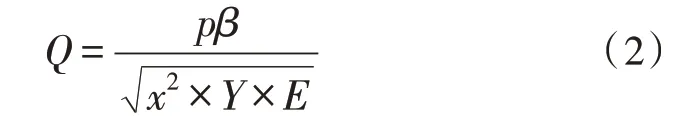
其中，x表示线路承载量；β表示等效置换系数；Y表示电缆线路能承载的最大振荡波动量；E表示局部漏电位置对于振荡波的平均负载条件。

对于线路振动脉冲的等效频率与脉冲特征量对应参考公式如下：

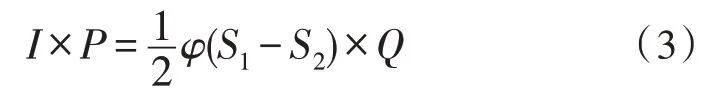
其中，φ表示配电线路的脉冲数值；Q表示电缆线路振荡波等效时频的基础寻优系数；S1、S2分别表示两个不同的振荡波脉冲向量[10-12]。

对于需要检测的配电线路来说，只需要计算出线路振荡波所放电的脉冲特征量和等效振动频率，然后将变量代入计算公式（3）。若等式两边的数值不相等，那么待测配电线路存在漏电点；若等式两边的数值相等，那么待测配电线路为安全线路。

2 配电线路漏电点定位

通过对配电线路内的脉冲信号进行特征提取，为建立配电线路漏电点定位模型提供数据基础。该文采用小波变换与奇异性检测方法获得配电线路内各个线路段的波动脉冲信号，具体配电线路漏电点定位信号的特征提取过程如下：

首先对需要定位的输电线路进行等段均分，然后采用小波变换算法获取和分解每段线路的振动脉冲信号。分解的数量根据实际线路长度而定，要保证信号的完整性和清晰性；

然后对分解的每段线路内的脉冲信号进行能量计算，计算公式如下：

其中，n表示线路切分的数量；k表示每段线路内切分信号的数量；xi为配电线路振动脉冲信号能量系数。

线路的分割长度是均等切分的，正常情况下，每段线路内脉冲信号的能量值都相同，一旦出现不同的线路段，那么此线路段一定存在漏电点[13-14]。根据计算的线路能量数值，舍弃与多数能量值相差数值较大的数据，计算出线路平均脉冲信号能量作为此线路正常脉冲信号的特征。配电线路漏电点线路运行电路图如图2 所示。

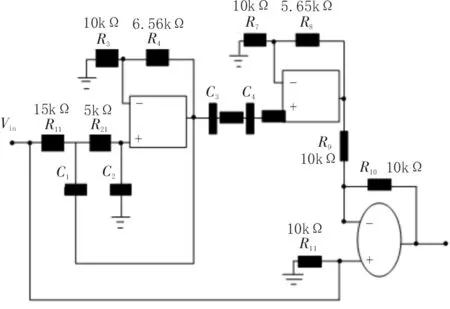
图2 配电线路漏电点线路运行电路图

将配电线路内脉冲信号的特征值以及正常状态下配电电路内的电压、电流、平均脉冲振动频率等相关振动参数进行关系匹配和约束，从而得到配电线路漏电点定位模型如下：

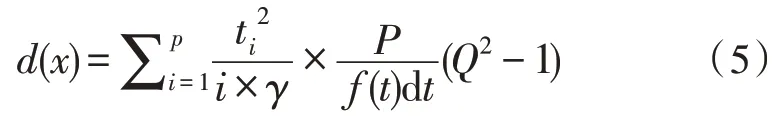
其中，i表示线路脉冲信号残差负荷矩阵；f(t)表示高斯函数；γ表示待测线路段内信号的方差贡献率；Q表示配电线路，其他位置的意义同上[15-16]。

将定位到具有漏电特征的配电线路段代入建立的配电线路漏电点定位模型内，即可完成配电线路漏电点的精确定位。配电线路漏电点定位原理如图3 所示。

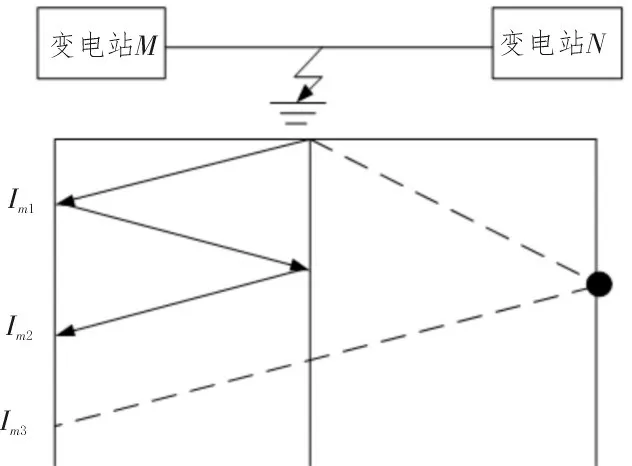
图3 配电线路漏电点定位原理

综上所述，总结具体的配电线路漏电点的定位流程如下：

步骤一：首先调用行波理论，计算出待检测配电线路内的振动脉冲波和等效频率，验证两个变量之间的关系，如果满足式（3），则进行复检。如果复检结果与第一次计算结果相同，那么停止配电线路漏电点的检测，直接输出正常。如果不满足式（3），那么执行步骤二；

步骤二：根据小波变换算法，完成待检测配电线路脉冲信号的分割以及能量计算，确定线路内存在漏电点的具体线路段；

步骤三：最后通过配电线路漏电点定位模型输出具体的线路漏电点，结束检测。配电线路漏电点的定位流程图如图4 所示。

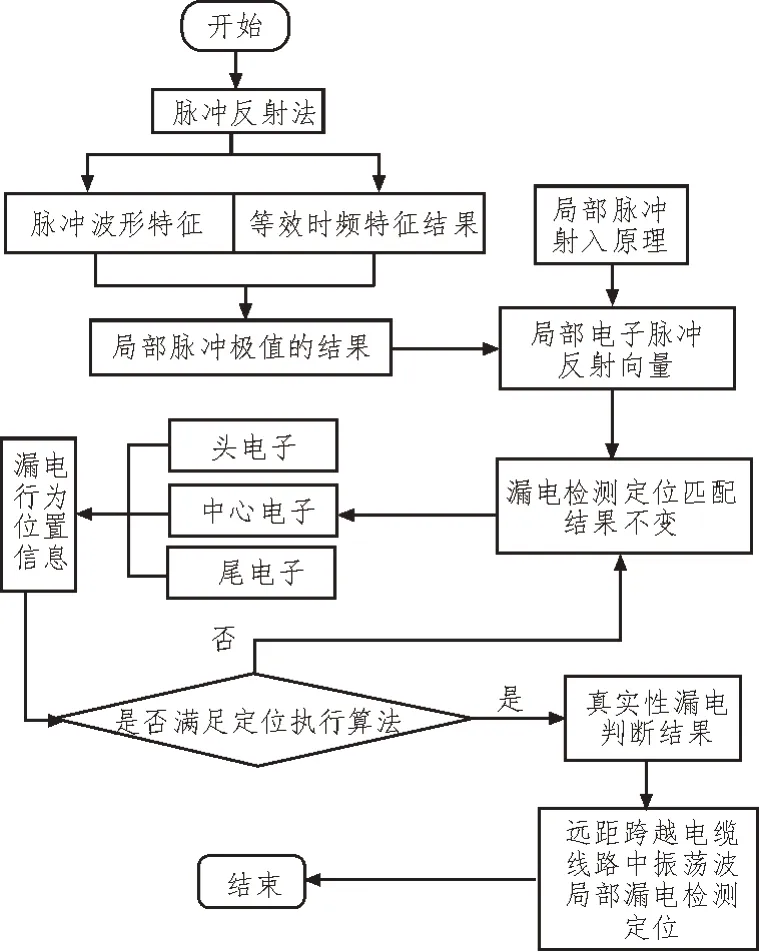
图4 配电线路漏电点定位流程图

3 实验与分析

为验证基于行波理论的配电线路漏电点检测与定位方法的实际应用性能，检验该方法对于配电线路漏电点的检测与定位的精度和准确度是否达到应用标准，在Matlab 环境中设计如下实验。

根据配电线路搭建规定，配电线路漏电点定位精度的标准为85%。为了降低实验对测试电力工程的干扰，选择IEEE1081.11 通信标准，实验的测试对象分别为单行配电线路和多行配电线路，以此避免实验测试结果出现偶然性。

实验选择的对照方法分别为基于震荡波的配电线路漏电点检测方法（传统方法1）和基于行波模量分析的配电线路漏电点检测与定位方法（传统方法2）。

因为实验的特殊性，在完成对实验测试环境的搭建后，在长春市配电线路管理中心等待。一旦管理中心接收到配电线路漏电故障，管理中心按照规定分配原始隶属部门进行配电线路漏电点的检测与定位的处理，同时也将相关信息发送到搭建的测试环境内，开始测试。

在测试过程中，记录3种方法的相关数据，方便实验的复盘与数据分析。直到3种方法分别完成对单行配电线路和双行配电线路的漏电点检测与定位测试后，结束实验。然后由系统删除相关配电线路的信息，完成实验数据整理，进行数据分析，得出实验结论。

对于单行配电线路的漏电点检测与定位，经实验可知，该文设计方法完成的时间为20 min，传统方法1 完成的时间为33 min，传统方法2 完成的时间为28 min。归纳实验进行过程中的数据，绘制结果图如图5 所示。

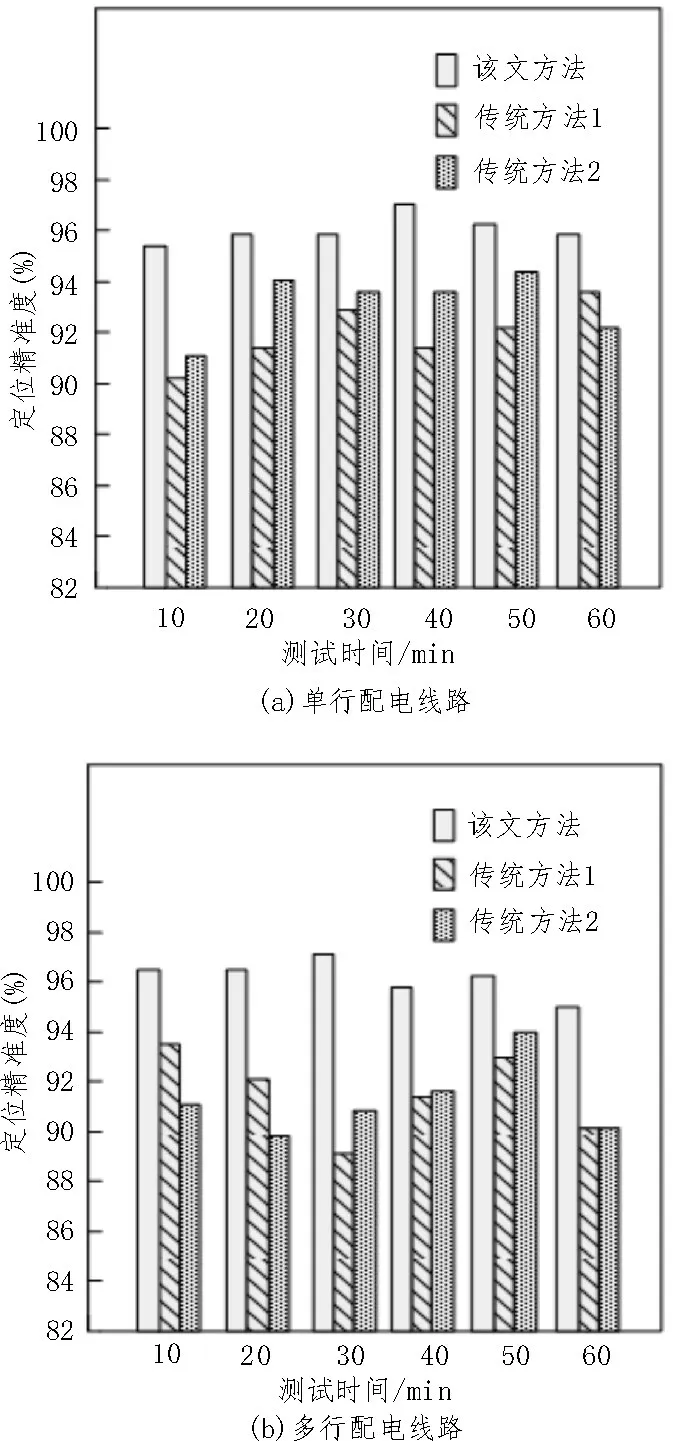
图5 定位精准度测试结果图

观察图5 可以看出，基于行波理论的配电线路漏电点检测与定位方法对于单行和多行配电线路的定位精准度最终都可以维持在95%以上，明显高于两种传统方法的定位精准度。综上所述，基于行波理论的配电线路漏电点检测与定位方法的定位精准度更高，充分证明了其应用性能。

在此基础上，为更直观地体现实验结果，整理图5中的实验数据，得到实验数据对比如表1 所示。

观察表1 可以直观地看出，无论对于简单的单行配电线路漏电点还是多行配电线路漏电点，该文设计的基于行波理论的配电线路漏电点的检测与定位方法均能达到一个较高的定位水准。综上所述，该文设计的基于行波理论的配电线路漏电点检测与定位方法的精准度最佳。

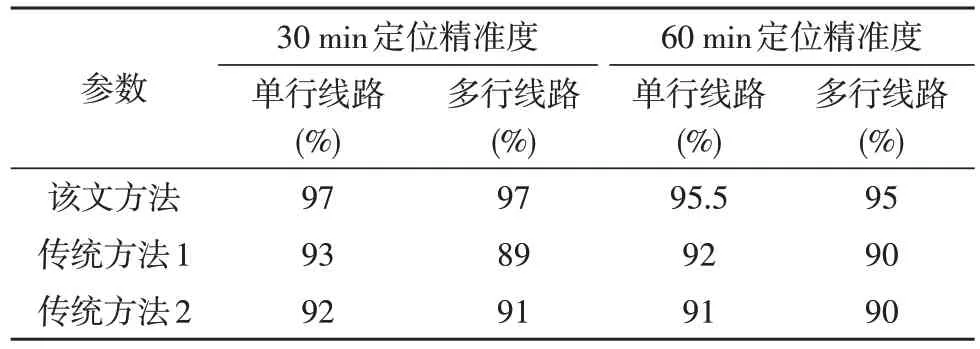
表1 实验数据结果

综上，可以得出基于行波理论的配电线路漏电点检测与定位方法具有较高的检测和定位精准度，证明其具备推广和使用的意义。

4 结束语

为有效避免因出现线路漏电而引起电力事故，该文提出了一种基于行波理论的配电线路漏电点检测与定位方法，该方法通过采用行波理论和线路振荡波放电脉冲波动反射检测原理设计配电线路漏电点定位模型，从而完成对多行电子和单行电子线路的漏电检测与定位，提高配电线路的维修效率。经过实验证明该文设计的方法比传统方法具有较高的推广意义和实用价值，可以提高配电线路的漏电检测效率。