考虑连接段厚度影响的风力机组合塔架优化设计*

郭兴文，姚皓译，蔡 新，张 远，张洪建

（1.河海大学 力学与材料学院，南京 211100；2.江苏省风电机组结构工程研究中心，南京 210098；3.沿海开发与保护协同创新中心，南京 210098）

0 引 言

国内低风速地区市场竞争日趋激烈，通过提升塔架高度获得更大的发电量是必然趋势。随着塔架高度的增加，传统钢塔面临制造、运输、频率穿越等问题[1]。钢-混组合塔架将混凝土塔和钢塔两种结构合理组合，能够满足风电机组对高度的要求，并且具有更好的安全性和经济性。塔架作为风电机组重要承载部件，承受着机组运行过程中产生的各种荷载，塔架不仅要有足够的强度、刚度和稳定性，其固有频率需避开风轮运行频率，避免与叶轮发生共振，其安全可靠性尤为重要。混凝土段与钢塔段的连接段是组合塔架结构的关键部件，连接段对结构的性能有重要影响。塔架制造成本约占整机成本的20%，在满足风电机组安全性的前提下，对塔架结构进行优化，降低成本显得十分重要。

近年来，国内外学者对不同类型塔架结构的优化设计进行了诸多探索性研究，推动了优化设计技术在该领域的发展。UYS 等[2]以成本为目标函数，以塔筒直径、塔筒壁厚、加劲肋数量与厚度为设计变量，对一个45 m 高的传统钢塔架进行优化设计，获得了成本最低时加劲肋数量与厚度的关系。陈俊岭等[3]结合某120 m 高度组合塔架，建立了以横截面几何尺寸、混凝土段高度和钢塔高度为设计变量，以整体稳定性和局部稳定性、强度、刚度和频率为约束条件，以塔架建设总成本为目标函数的优化设计模型并进行了优化，指出组合塔架混凝土段高度为塔架总高度的67%时整体造价最低。陈逸杰等[4]对轮毂高度分别为85.0 m、102.5 m 和122.0 m 的2.5 MW 风力机组合塔架进行优化，结果表明组合塔架混凝土段高度为塔架总高度的74%时整体造价最低。许斌等[5]开展了组合塔架混凝土段高度、钢塔段高度以及截面尺寸的优化，指出当混凝土段的高度接近塔架总高度的70%时造价最低。对组合塔架而言，连接段的设计对结构的性能及建设成本均有重要影响，相关学者对此也开展了进一步的研究。许斌等[6-7]提出了混凝土填充钢箱和穿筋连接的方案，研究表明所设计方案的结构受力性能明显优于传统法兰盘连接。谢咏剑[8]对一种嵌入式开孔板和穿孔钢筋结构连接方案进行了有限元计算，综合分析指出在法兰盘下部设置嵌入式钢筒和穿孔钢筋能有效提高连接段刚度并改善应力分布，可以避免传统法兰盘连接因刚度不足而出现与混凝土分离的现象，该研究表明组合塔架连接段需要精心设计，以确保整体结构的安全。上述研究工作为组合塔架设计质量的提升提供了重要的依据，建立包含连接段厚度等参数的优化设计数学模型并进行优化设计，对提升组合塔架设计质量意义重大。

本文以某3 MW 风力机组合塔架为研究对象，构建了以各塔段外径、壁厚、连接段厚度和混凝土段高度等关键几何尺寸为设计变量，以塔架固有频率、关键部位应力、塔顶位移和稳定性等关键性态指标为约束条件，以塔架成本为目标函数的优化设计数学模型，采用有限单元法进行结构计算分析，在Workbench 平台上进行塔架优化设计，对结果进行详细分析。

1 组合塔架参数

3 MW 组合塔架由4 段组成，其中底部第Ⅰ段为混凝土段，高度为55 m，Ⅱ、Ⅲ、Ⅳ段为钢塔段，三段钢塔高度合计82.8 m，塔架总高度为137.8 m。上部三段钢塔筒之间通过法兰盘连接，底部混凝土段通过其顶部的钢垫板与第Ⅱ段钢塔筒下部的法兰盘实现连接，沿混凝土塔壁竖向设置24 束预应力钢绞线，每束包含9 根低松弛钢绞线（1×9φs15.2），组合塔架结构及连接段如图1 所示，各段的内外径及壁厚参数见表1。

图1 组合塔架示意图Fig.1 Diagram of hybrid tower

表1 组合塔架设计参数Table 1 Design parameters of hybrid tower

组合塔架的钢塔段、法兰盘、钢垫板采用Q355钢材[9]，根据各部件不同厚度并参考规范[10]取安全系数为1.1，钢塔段材料的设计强度为313.6 MPa，法兰盘与钢垫板材料的设计强度为268.2 MPa；混凝土段强度等级取C60，对应抗拉强度设计值为2.04 MPa，抗压强度设计值为27.5 MPa[11]。组合塔架材料参数取值见表2。

表2 组合塔架材料参数Table 2 Material parameters of hybrid tower

2 组合塔架优化模型

2.1 设计变量

为反映组合塔架整体特征，综合考虑后选取以下关键几何参数为设计变量：混凝土段底部外径（d1）和壁厚（t1）、混凝土段顶部外径（d2）和壁厚（t2）、混凝土段高度（h）、钢塔段底部壁厚（t3）、钢塔段顶部外径（d3）和壁厚（t4）。为了反映连接段这一关键部位，在上述设计变量的基础上增加了连接段的关键几何参数：钢垫板厚度（t5）、法兰盘厚度（t6）。参考工程经验和相关设计规范，设计变量取值范围如表3。

表3 设计变量取值范围Table 3 Value scope of the design variables

2.2 约束条件

约束条件是组合塔架优化设计中寻找目标函数最值的多个限制条件，塔架结构设计时必须使各部件具有足够的强度、刚度和稳定性，塔架在各种荷载作用下会产生振动，应避免塔架与叶片的共振。本文优化中的约束条件如下。

（1）频率约束。为了防止塔架与叶片发生共振，一般要求塔架的固有频率与叶片转动频率及叶片通过频率都有10%以上的间隔，本文塔架的固有频率须满足下式：

式中：f0,1为塔架的第一阶固有频率；fR为正常运行运行时叶片的最大旋转频率；fR,3为3 倍的叶片旋转频率。

（2）最大位移约束。参考《高耸结构设计规范》[12]规定的塔架许用挠度应控制在塔架总高度的1/150以内，塔架最大位移约束计算公式为：

式中：dmax为塔架顶部最大水平位移；为塔架顶部最大容许水平位移。

（3）钢塔段应力约束。钢塔最大应力不超过设计强度。

式中：σe,max为钢塔全段内的最大等效应力；fy1为钢材的屈服极限；γm为材料的安全系数。

（4）连接段应力约束。钢垫板和法兰盘的最大应力不超过其设计强度。

式中：σmax为连接段法兰盘和钢垫板的最大等效应力；fy2为连接段钢材的屈服极限。

（5）混凝土段应力约束。最大拉压应力不超过强度设计值。

式中：σt为混凝土段最大拉应力；σc为混凝土段最大压应力；ft为混凝土抗拉强度设计值；fc为混凝土抗压强度设计值。

（6）稳定性约束。保证钢塔局部稳定，考虑钢塔段最大应力不超过塔筒局部稳定的临界应力值；保证塔顶在特定的外荷载作用下塔架的整体稳定性，塔架的第一阶临界屈曲荷载要大于轴向荷载的1.1 倍。

2.3 目标函数

目标函数是判别一个设计方案优劣标准的数学表达式，反映了结构中某一个最重要的特性或指标。工程结构的优化目标一般从施工技术、经济角度等方面进行考虑，比如结构的总体积最小、结构总造价最低等。本文以组合塔架总成本最低为优化目标。其计算公式如式（7）所示。

式中：F为组合塔架材料总价格；V1为混凝土段总体积；M1为连接段部件总质量；M2为钢塔段总质量；A1为混凝土单价；C1为连接段材料单价；C2为钢塔筒单价。

本文根据某风电项目材料的平均价格来确定所选材料价格，泵送C60 混凝土造价为720 元/m3；法兰盘和钢垫板材料价格为13 600 元/t；钢塔筒材料价格为9 200 元/t。

2.4 优化模型

综合上述分析，3 MW 风电机组组合塔架的优化设计数学模型如下。

设计变量：X=[d1，d2，d3，h，t1，t2，t3，t4，t5，t6]T

使目标函数：F=720V1+13 600M1+9 200M2→min

3 结构有限元分析

考虑到结构的复杂性以及各部件的细部特征，本文采用有限单元法进行结构分析。

3.1 有限元模型

组合塔架结构通过Creo 参数化建模并导入Ansys Workbench 中。塔架简化为底端固定的结构。混凝土采用solid65 实体单元，每束预应力钢绞线通过多点约束（multi-point constraints,MPC）算法将预应力钢绞线的两端约束在上下两锚具与塔架的接触面上，预应力钢绞线采用link180 杆单元，预应力的加载方式采用等效荷载法，即将钢绞线的作用以荷载的形式施加于结构。塔架承受上部结构重量采用MASS21 质量单元来考虑，并通过MPC184 多点约束单元将质量单元和塔架连接。钢塔、法兰盘、钢垫板采用solid186 实体单元。

为了保证网格的质量，网格划分时，通过切割实体避免出现不规则的几何体以确保单元质量，采用多区域划分技术。整个塔架结构剖分后的单元总数为419 110 个，节点总数为353 360 个，网格划分结果如图2 所示。在数值模拟中，钢塔段与段之间采用绑定接触；法兰盘与钢垫板采用面面接触，法向属性采用摩擦接触，接触面之间可以传递压力而不传递拉力，接触面之间的切向属性采用“有限滑动”模型，接触面摩擦系数取0.3[13]；钢垫板与混凝土顶面采用绑定接触；预应力混凝土段与段之间通过C80 座浆料与预应力钢绞线连接，使其成为预应力混凝土整体结构，混凝土段与段之间采用绑定接触。通过不同网格的尺寸进行网格无关性的验证，该网格尺寸满足精度要求。

图2 组合塔架整体网格Fig.2 Mesh of hybrid tower

风力发电机组应能承受所确定的安全等级的风况，从荷载和安全角度考虑，风况可分为风力机正常工作期间频繁出现的正常风况、1 年或50 年一遇的极端风况[14]。塔架受到气动推力、惯性力、重力荷载和其他荷载的共同作用，通常利用GH Bladed风机设计软件计算出各工况下的荷载数据。由于设计荷载工况种类过多，选取了额定工况和极限工况荷载值作为塔架顶部承受的荷载，塔架顶部所承受的荷载可分解成x、y、z方向的力和弯矩[15]，最大荷载如表4 所示。

表4 不同工况下的塔顶荷载Table 4 Load on top of tower under different conditions

3.2 初始方案的评估

为了解初始方案的性能以及检验其是否为可行方案，在两种工况下对组合塔架初始方案进行数值模拟。图3a 为组合塔架一阶频率对应的振型图，塔架的一阶固有频率为0.321 Hz，风电机组的旋转速度为7～ 12.6 r/min，对应旋转频率为0.117～ 0.21 Hz，塔架固有频率与叶片转动频率及叶片通过频率都有10%以上的间隔[16]，不会发生共振；图3b 和图3c为额定工况和极限工况下组合塔架水平位移云图，塔顶水平位移分别为420.12 mm、853.68 mm，符合设计要求。

图3 （a）一阶固有频率；（b）额定工况下塔架水平位移；（c）极限工况下塔架水平位移Fig.3 (a) First order natural frequency;(b) horizontal displacement of the tower under rated working conditions;(c) horizontal displacement of the tower under extreme working conditions

图4～ 图7 为额定工况和极限工况下各部件应力云图。钢塔段等效应力最大值出现在背风侧与法兰盘接触处，最大值为213.77 MPa，小于材料的设计强度。连接段法兰盘等效应力最大值为265.23 MPa，钢垫板等效应力最大值为111.99 MPa，连接段满足设计强度要求，连接段应力最大值出现在迎风侧预应力钢绞线孔道附近，由于此处布置了预应力钢绞线，容易产生应力集中现象，因此上述结果是合理的。额定工况下混凝土段竖向全部受压，竖向最大压应力为24.02 MPa，均小于C60 混凝土强度设计值。极限工况下混凝土段绝大部分竖向受压，局部出现了较小的拉应力；竖向最大压应力为26.45 MPa，出现在背风侧顶部；最大拉应力为1.72 MPa，出现在迎风侧顶部，满足规范要求。

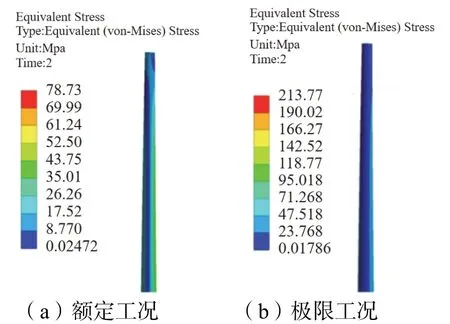
图4 两种工况下钢塔等效应力Fig.4 Equivalent stress of steel tower under two working conditions

初始方案的计算分析表明，塔架各项性能指标满足规范要求，是一个可行的设计方案，各种性能指标均有一定的余量，存在一定的优化设计空间。

图5 两种工况下混凝土竖向正应力Fig.5 Vertical normal stress of concrete under two working conditions

4 优化设计及结果分析

采用第2 节的优化设计数学模型，在Workbench平台上完成组合塔架的优化设计。表5 为优化过程前后各设计变量的取值。由表5 可知，混凝土段的高度较初始方案的高度增加了30.3 m，变化最为显著，优化后的钢塔架底部壁厚有所增加，顶部壁厚有所减小；优化后的法兰盘和钢垫板厚度均有所减小；混凝土段底部和顶部外径、壁厚有所减小。针对本文案例，混凝土用料增加了47.1%，钢塔用料减少了 26.5%，塔架总成本比初始方案减少了15.7%，优化效果明显。进一步的分析表明，混凝土段高度占塔架总高度的61.9%时成本最低；法兰盘占连接段总厚度的76.2%时受力性能最佳。

表5 优化前后的设计变量Table 5 Design variables before and after optimization

表6 给出了优化前后关键性态指标的结果。由表6 可知，所有的性能指标都满足要求，其中塔顶位移约束条件接近临界约束条件，是一个约束最优解。优化方案塔顶直径、壁厚、连接段厚度减小，组合塔架上部钢塔总体刚度有所降低，组合塔架一阶固有频率有所减小；连接段钢垫板和法兰盘等效应力最大值均有所增加。综合分析表明组合塔架整体结构优化设计方案是安全可靠、经济合理的。

表6 优化前后关键性能指标Table 6 Key performance indicators before and after optimization

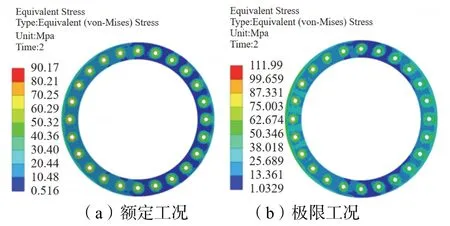
图7 两种工况下钢垫板等效应力Fig.7 Equivalent stress of steel plate under two working conditions

5 优化方案疲劳校核

疲劳寿命预测是组合塔架校核的主要内容之一。根据GL 2010 规范[10]在GH Bladed 软件中计算出组合塔架的随机疲劳荷载，在nCode 中计算分析得到各部件的疲劳累积损伤。图7 为各部件疲劳累积损伤图，由图可知，垫板、法兰盘和钢塔的疲劳累积损伤分别为0.867、0.733 和0.796，各部位的损伤值都小于1，满足要求。

图7 钢制部件疲劳累积损伤图Fig.7 Fatigue cumulative damage diagram of steel components

6 结 论

为提高组合塔架结构的安全性能以及降低塔架成本，构建了包含连接段厚度的塔架优化设计数学模型，对某3 MW 风电机组组合塔架进行了优化设计，主要结论如下：

（1）对组合塔架整体结构的优化设计切实可行，可为实际工程提供更加经济合理的方案。

（2）对组合塔架而言，混凝土段的高度占总高度的比例对整体的性能与成本有着重要影响，综合分析混凝土段高度为塔架总高度的60%～ 75%时塔架总成本相对较低。

（3）考虑连接段厚度的优化模型能有效调整连接段的受力性能，有利于提高塔架整体优化的效果。