基于ANSYS Workbench的直升机尾传动轴临界转速研究
黄 锋
(中国直升机设计研究所,江西 景德镇 333001)
0 引言
尾传动轴负责将发动机输出的转速和扭矩传递给尾桨叶,其结构性能和动特性在很大程度上影响直升机的操作性和可靠性。尾传动轴转速高、负荷大的工作特性和质量轻、管壁薄的结构特性使其成为故障率较高的部位。在动力传动轴动力学的设计过程中,确定临界转速是最基础也是最重要的一环。基于尾传动轴的工作特性并配置合理的临界转速是保障尾传动轴安全运行的前提。因此,为了从动力学角度分析设计的合理性,在传动轴设计的各阶段都必须对临界转速进行研究。通常采用传递矩阵法和有限元法计算临界转速。有限元法与传递矩阵法相比,它需要占用更多的计算机存储空间。随着现代计算机的发展,使用有限元法计算传动轴临界转速在计算时间和计算量上已经不存在困难,且其计算结果的精度更高。因此,该研究采用有限元法对直升机尾传动轴临界转速进行研究。该文以直升机尾传动轴转子系统为对象,基于ANSYS Workbench并运用有限元方法建立了尾传动轴转子系统的有限元模型,分别研究轴承位置、轴管厚度和轴承刚度对尾传动轴临界转速的影响。
1 尾传动轴有限元模型
该文为了研究轴承与尾传动轴的动特性关系,建立了尾传动轴转子系统的有限元模型。根据Timoshenko梁理论,对尾传动轴进行离散化处理,将传动轴分为个单元,共有+1个节点,每个单元共用1个节点,每个节点有5个自由度(3个平移自由度和2个旋转自由度),如图1所示。

图1 尾传动轴单元有限元模型
节点位移向量如公式(1)所示。

运用广义哈密顿原理可以得到公式(2)。

式中:和分别为梁单元的动能和势能;为外力做的功;为时间。
单元的总动能是平移动能与转动动能的总和。梁单元的总动能如公式(3)所示。


梁单元的总势能包括梁的弹性弯曲势能、切变形势能和梁的轴向压缩形变势能,梁单元的总势能如公式(4)所示。
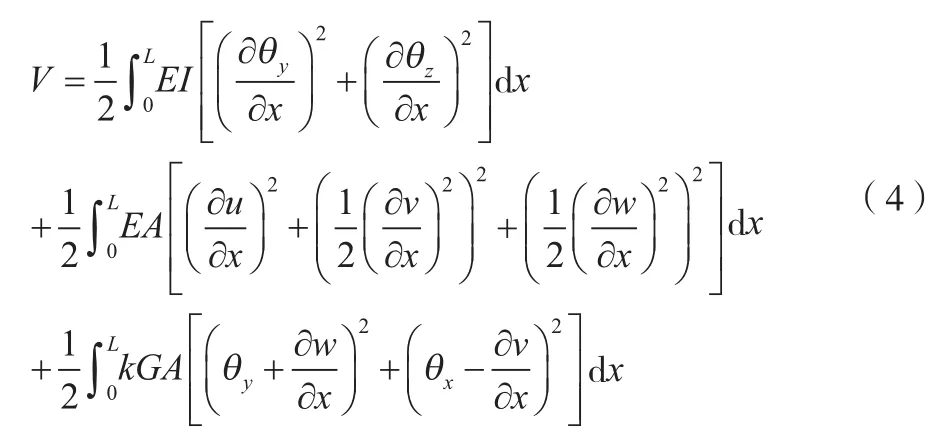
式中:为弹性模量;为轴惯性矩;为截面面积;为剪切系数;为剪切模量。
外力做功如公式(5)所示。

式中:q、q以及q分别为在、以及方向上的分量(为节点位移向量);为梁单元质量。
将公式(3)~公式(5)带入公式(2)中,尾传动轴转子系统的动力学微分方程如公式(6)所示。


尾传动轴——深沟球轴承系统的刚度矩阵如公式(7)所示。

式中:[K]为传动轴的刚度矩阵;[K]为轴向力引起的刚度矩阵;[K]为深沟球轴承刚度矩阵;[M]为考虑离心力效应的附加矩阵。
2 临界转速有限元分析
2.1 尾传动轴转子系统结构
建立尾传动轴转子系统,如图2所示,尾传动轴由2个深沟球轴承支撑,前端通过法兰盘与主减速器输出轴连接,后端通过花键与尾减速器连接,轴承由轴承支座与机身连接。尾传动轴参数见表1。

图2 尾传动轴转子系统结构

表1 尾传动轴参数表
2.2 轴承位置对临界转速的影响
该研究运用ANSYS Workbench求解尾传动轴转子系统的临界转速。为了研究轴承位置对传动轴临界转速的影响,将2个轴承设置为与轴管两端距离相同,如图3所示,假设轴承距离尾传动轴两端距离为,分别计算了=1/12、=1/6、=1/4、=1/3以及=5/12时转动轴的临界转速。首先,使用三维建模软件CATIA建立传动轴三维数模。其次,将模型导入ANSYS Workbench中,传动轴转子系统的三维数模如图4所示。

图3 轴承位置示意图

图4 传动轴转子系统的三维数模
轴承内圈通过轴套与传动轴过盈配合,轴承外圈通过轴承支座与机体连接。轴承对传动轴的支撑可以简化为各个角度的弹簧阻尼器,如图5所示。水平垂直的正交弹簧阻尼器的刚度系数、和阻尼系数、,45°倾斜的正交弹簧阻尼器的刚度系数、和阻尼系数、。如果、、以及为0,那么转子系统的翼型轨迹为圆形,否则转子系统的运行轨迹为椭圆形。 此时,将、设置为10N/mm,将C、设置为2 N·s/mm,其他参数设置为0。根据实际的工程应用情况,选取传动轴振动的前三阶模态。轴承位于=1/3时传动轴的前三阶模态振型和坎贝尔图如图6、图7所示。根据临界转速的定义,临界转速值为同步曲线与各阶固有频率曲线的交点。

图5 轴承刚度及阻尼系数设置

图6 尾传动轴的前三阶模态振型

图7 坎贝尔图
通过ANSYS Workbench计算得到轴承在不同位置对应的临界转速,见表2。

表2 轴承位置对临界转速的影响
图8为轴承位置对传动轴临界转速的影响曲线图。由图8可知,当2个轴承逐渐靠近传动轴中部时,各阶临界转速都会增加(增加的速度不相同);当临界转速增加到某一值时,再随着2个轴承逐渐靠近而逐渐变慢。一阶临界转速在轴承位于1/3时达到最大,二阶临界转速和三阶临界转速在轴承位于1/4时达到最大。直升机的尾传动轴实际转速低于一阶临界转速,该轴为亚临界轴。根据公式(8)可知,轴承位置在1/12、1/6以及1/4时所对应的临界转速不符合要求。在实际设计中,2个轴承的位置位于1/3附近,此时临界转速与实际转速的裕度最大,研究结果与实际设计情况相符。

图8 轴承位置对传动轴临界转速的影响曲线图

式中:为轴的工作转速;为轴的一阶临界转速。
2.3 轴管厚度对临界转速的影响
轴管的横截面如图9所示。保持轴管外径不变,改变轴管内径,轴管厚度=(-)/2。该研究分别计算了厚度为1 mm~5 mm的轴管所对应的临界转速,其结果见表3和图10。结果表明,增加轴管厚度会降低传动轴临界转速,由拟合曲线可以发现,轴管厚度对临界转速的影响呈(近似)线性关系。

表3 轴管厚度对临界转速的影响
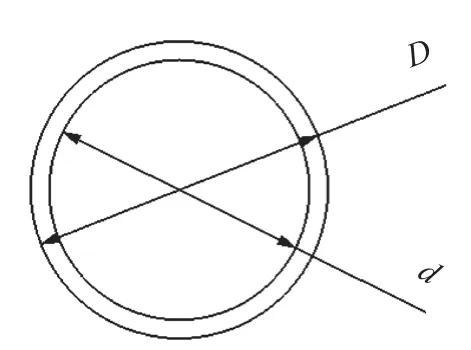
图9 轴管厚度示意图
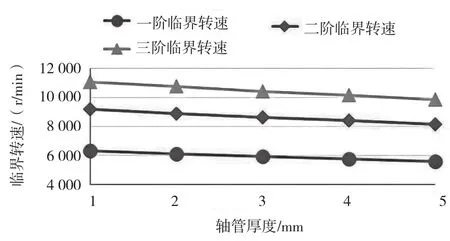
图10 轴管厚度对临界转速的影响曲线图
从研究结果可知,轴管厚度越小,工作转速与临界转速的差值越大,尾传动轴越不容易出现共振现象。但是管壁厚度过小也会导致结构刚度变小,传动轴可能会出现结构破坏的现象,因此,在设置管壁厚度时,应该考虑多方面的影响因素。
2.4 轴承刚度对临界转速的影响
尾传动轴转子系统采用深沟球轴承支撑,设置轴承刚度从1×10N/mm增大至6×10N/mm,尾传动轴转子系统的前三阶临界转速变化情况(见表4与图11)。由表4和图11可知,轴承刚度对各阶临界转速的影响很小,这可能是因为轴承刚度大于传动轴自身的刚度,属于刚性支撑。此时的临界转速与传动轴自身的刚度和质量关系较大(更大数值范围的轴承刚度的变化对临界转速的影响有待进一步研究)。

图11 轴承刚度对临界转速的影响曲线图
3 结论
该文以直升机尾传动轴为对象,基于ANSYS Workbench并运用有限元分析方法研究轴承位置、轴管厚度和轴承刚度对某直升机尾传动轴临界转速的影响。结果表明,在2个轴承逐渐从传动轴两端移动到传动轴中部的过程中,临界转速先提高后降低;尾传动轴为亚临界轴,一阶临界转速在1/3时达到最大,与实际情况相符。增加轴管厚度将导致尾传动轴临界转速降低,并且其以线性趋势降低。实际工程中的轴管厚度为2 mm,在保证尾传动轴有足够刚度的同时,确保临界转速与实际工作转速存在足够裕度。在一定数值范围内,轴承刚度对尾传动轴临界转速的影响较小。
该研究可为设计尾传动轴时避开其临界转速提供相应的参考,还可以指导直升机尾传动轴组件的设计优化,从而保证转子系统结构的可靠性。

