基于电磁感应原理的单摆法测量重力加速度

魏 杰，易家乐，喻慧琴，杨 帆，田 勇，何小风，里 霖，胡晓军

(1.武汉理工大学 交通与物流工程学院，湖北 武汉 430070；2.武汉理工大学 理学院,湖北 武汉 430070)

重力加速度参数广泛应用于地球物理、空间科学、航空航天等领域.高精度的重力加速度值的测量对重力场模型建立与完善、自然灾害预警、矿物勘探、大地水准面绘制等领域有着重要的作用[1,2].重力加速度测量方法主要有单摆法、自由落体法、平衡法、滴水法、斜面法、平抛法等[3-5].这些方法的测量原理都是将本地重力加速度值与特定的运动形式联系起来.此外，在科研领域最为精确的测量重力加速度的方法为原子干涉法[6]，该方法对于设备以及测量环境的要求非常高.

在众多重力加速度测量方法中，单摆法具有装置简单且操作方便的优点，因此成为物理教学实验中常用的测量重力加速度的方法[7].该方法是借助本地重力加速度值与单摆简谐振动周期T之间的关系，通过测量单摆摆长和周期数据，从而实现重力加速度值的测定.准确测量单摆运动周期T是实现高精度重力加速度值测量的关键.

然而，传统的单摆法一般是借助秒表和人工计时来测量T的.由于人为误差等因素，在周期记录上往往存在较大误差，而且这种误差是无法具体量化分析的.针对这一问题，实验工作者对单摆装置进行了相应的改进.例如，孙阿明[8]借助激光器以及光电探头组成类似于“光电门”的实验装置，使单摆在摆动过程中出现周期性的遮挡动作，导致光电探头内的光敏二极管的光信号出现周期性变化，从而测定单摆的周期T.此外，姜先策和张宏菊[9]利用霍尔开关传感器对单摆装置进行改进，实现了周期的多次测量，提高了周期测量的准确性.

1 工作原理

本文设计了一种基于单摆法结合电磁感应原理的本地重力加速度值的测量方案.该方案成功地将单摆的周期运动与线圈内部感应电动势信号建立联系.实验信号由示波器采集，实现了单摆运动周期的“可视化”.本设计的实验方案不仅可以快速地实现重力加速度值的准确测量，同时也简化了相应测量装置的安装，降低了对实验环境和硬件配置的要求.

1.1 理论重力加速度

地表的物体受到的万有引力F可以看成是重力mg和自转向心力Fr的合力，即

F=mg+Fr

(1)

如果认为地球是均匀的刚体，则F的大小在不同经纬度地点是相同的，但是Fr的大小却是随纬度φ的变化而变化的，有

Fr=mrω2cosφ

(2)

此处r为地球半径，ω是其自转的角速度.本实验地点为湖北省武汉市.据此，将武汉市的φ值代入上式，得到武汉市重力加速度的参考值为g=9.793 6 ms-2，此为理论重力加速度.

1.2 方案设计原理

本方案设计的主体思路是借助单摆的简谐振动周期T与本地重力加速度g之间的关系：

(3)

其中l0是单摆摆线的长度，r是摆球的半径，二者之和代表单摆的摆长.这两个量在实验室可以通过多次测量达到希望的数据精度.可见，应用单摆法测量本地重力加速度的关键是如何实现周期T的准确测量.

本设计方案将电磁感应原理与单摆的周期运动相结合，将单摆的周期运动转化为感应电动势的周期变化，实现周期的准确测量.图1是设计原理的示意图.如图1左图所示，本方案使用永磁球体作为摆球，在其正下方放置由纯铜漆包线制作的多匝线圈.当永磁球体在线圈上方做往复运动时，将导致线圈内部磁通量发生周期变化，从而出现周期性的感应电动势信号.使用示波器记录这一信号，实现单摆运动到电动势信号的转化.明显的，只要准确记录了电动势信号，就可以得到单摆的运动周期.

图1右图是在一次实际测量过程中采集的电动势信号.图1左图和右图之中所标记的数字是对应的，表示磁球的运动与电动势信号之间的对应关系.为了获得较为明显的电动势信号，本文使用了多匝线圈(本次实验为80匝)，平铺在一个平面之上.所以，最终示波器采集到的电动势信号是多个存在一定相位差的信号的叠加，并非理想的简谐函数曲线.这并不影响准确判断信号的周期，如图1所示，点1到点9之间的时间间隔即为单摆的运动周期.由于不能保证磁球的平衡位置正好处于线圈中心的正上方，图1中信号幅值并不完全相等.明显的，这并不影响周期的判读.

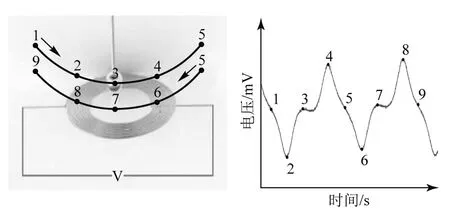
图1 实验设计原理示意图

在磁球运动过程中，线圈之中的感应电流会产生附加磁场，此磁场将会与磁球相互作用，可能使得磁球的运动偏离简谐振动规律.本文认为此电磁阻尼是可以忽略的.首先，测量的电动势信号一般在20 mV以内，在测量电动势信号时，实验选取内阻是1 MΩ的示波器，这样可以极大的弱化线圈之中的感应电流.下文粗略估计了阻尼的量值范围，大约是重力量值的10-12.此外，在实验装置设计时，在线圈下方安装了升降台(见下文)，通过改变线圈与磁球之间的垂直距离，从而改变感应电动势和电流，最终改变电磁阻尼的大小.实验测量了多个不同距离下的周期和对应的重力加速度，发现相互之间的差别完全在误差范围之内，并且不呈现规律性，从而在实验上证明了电磁阻尼是可以忽略的.

2 实验装置

本文设计的实验装置如图2所示.该装置使用电木板作为整个装置的底座，使用有机玻璃(亚克力)作为立杆，使用铝合金横杆用于固定摆线.横杆末端是两块铝片，将摆线置于其间并使用螺丝夹紧.使用无弹力柔线作为摆线，摆线末端与永磁球体连接，连接处使用环氧树脂做黏结，力图使得二者之间满足点接触的理想状态.磁球下方是使用细铜丝制作的80匝感应线圈.线圈固定于亚克力平台之上，平台高20 cm.平台与升降台连接，升降台通过螺钉固定在底座上面.升降台侧面有刻度，精度为0.1 mm.升降台可以使亚克力平台上下移动50 mm，用来改变线圈与磁球之间的垂直距离.在亚克力平台上端设计了卡槽，用来限定拨杆的运动.磁球的静止释放是通过一根塑料拨杆实现的，首先将拨杆插入卡槽，将磁球缓慢拨到预先设定的偏离位置，继续向外沿卡槽水平移动拨杆，磁球将自动释放.相比于直接使用手释放，这种方式可以避免磁球在摆动的同时可能出现的转动.线圈两端与滤波器连接，信号通过滤波器滤除噪声之后被示波器采集.

本文发现即使将磁球移开，静置线圈两端也可以产生幅值大约为5～10 mV的噪声信号，并且噪声的频率在50 Hz以上.噪声将严重影响对于周期的判读，使得实验方案基本不可实现.考虑到单摆运动的频率大约在1～2 Hz，本实验设计了一种低通滤波器模块.当信号频率高于10 Hz时，低通滤波器将会过滤掉这些信号，仅允许10 Hz以下的信号通过.滤波器需要提供5～10 V的恒定电压方可正常工作，本实验使用大学物理实验室通用的恒压源供电，图2中未画出.

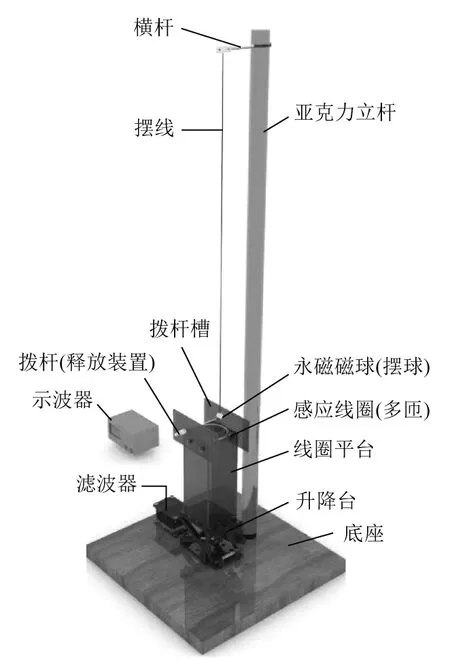
图2 实验装置(导线及恒压源未画出)

3 实验过程

实验数据的采集过程如下：

Step1：使用游标卡尺测量磁球的直径，多次测量取均值.

Step2：在悬挂状态下使用精度为1 mm的米尺测量摆线长度，测量10次取均值.

Step3：调节升降台，使得线圈与磁球尽量靠近.本次实验将这个最近距离d0选择在3 mm左右.

Step4：使用恒压电源给滤波器供电，设置示波器时基和电压显示分度，选择触发电平为2 mV，上升沿触发模式.

Step5：将磁球静止置于线圈正上方，使用拨杆缓慢拨动磁球，使其偏离平衡位置.继续水平移动拨杆，磁球在预定的摆幅位置释放.本次实验摆长约为70 cm，计算之后得到摆球偏离平衡位置只要不大于6 cm就可以保证磁球的运动是简谐振动，即摆角小于5°.一般使其离开平衡位置4 cm时释放.

Step6：在磁球摆动过程中按下示波器“单次触发”按钮，示波器将自动触发并且记录电动势信号.

Step7：在示波器上使用光标工具判读周期，也可以将数据转移到电脑使用其它软件(如绘图软件Origin)精确判读.示波器可以设置较长时基，这样可以采集到多个周期的信号，如图3所示.

Step8：调节升降台，改变线圈与磁球之间的相对高度，重复步骤Step4—Step7.

4 实验结果与分析

4.1 实验结果

本次实验使用的摆线长为0.694 2 m，摆球直径为14.90 mm，所以单摆摆长为0.701 7 m.周期判读一般选择4～6个周期时间然后取平均(如图3所示)，这样可以进一步降低周期的不确定度.每次磁球与线圈之间的高度改变值为5 mm.本文将实验结果列在表1之中，并且绘制在图4之中.图4实线是武汉市重力加速度的参考值，9.793 6 m/s2.

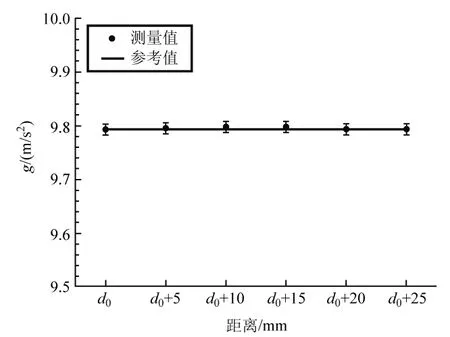
图4 测量的本地重力加速度实验值

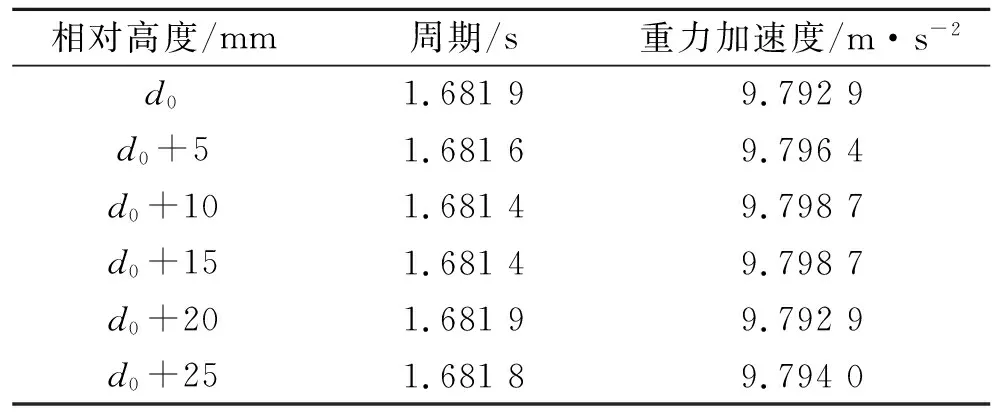
表1 本地重力加速度的测量结果

由表1结果可见，本实验测量的武汉市重力加速度与参考值有很好的一致性，说明本设计是成功的.此外，不同高度下测量的结果之间并没有明显的差别，说明电磁阻尼对于单摆运动的影响可以忽略.

4.2 电磁阻尼的半定量分析

虽然实验上证明了电磁阻尼可以忽略，本文仍然通过简单的动力学和电磁学基本知识对于电磁阻尼问题进行了半定量分析.对于含阻尼的小角振动，其运动学方程可以写为

(4)

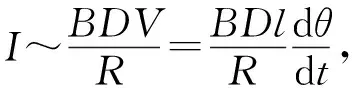
(5)

将上式代入方程(4)同时考虑小角振动(θ<5°,sinθ～θ)，

(6)

解这个微分方程得到

(7)

上式右侧第二项代表阻尼的影响.取N=80，B=1 T，D=0.1 m，l=0.7 m，m=0.1 kg，R=1 MΩ(示波器内阻)，粗略估算此阻尼项数量级约为10-12.如此小的阻尼完全是得益于极高的示波器内阻的缘故.总之，电磁阻尼对于重力加速度的影响很小，可以忽略不计，这与实验结果是一致的.

4.3 系统误差分析

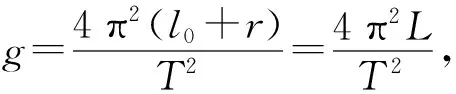
lng=2ln 4π+lnL-2lnT

(8)

对上式求全微分

(9)

在进行随机误差分析时，将“-”号变成“+”号，同时“d”变为“Δ”，则

(10)

由上式可以看出重力加速度的误差来源于摆长和周期测量.

周期测量的误差主要来源于示波器的测量误差，摆长的误差来源主要是米尺精度造成的测量误差.

(1)摆线长度不确定度

本实验摆线长度通过米尺测量10次，得到此次实验装置摆长的A类不确定度分别为0.000 148 m.米尺的最小单位长度为1 mm，通过公式

(11)

得到摆长的B类不确定度为0.000 288 675 m.

(2)磁球半径尺寸不确定度

通过游标卡尺测得磁球半径为14.90 mm，本次实验所使用的游标卡尺是50分度游标卡尺，由于磁球直径的多次测量值并无明显变化，且对实验结果影响并不大，因此将A类不确定度视为0，只考虑B类不确定度，通过公式

(12)

得到磁球半径尺寸不确定度为0.000 011 547 m.

(3)周期不确定度

摆线长度不同时，实验测得的周期也不同，摆长越长，周期越大，针对一定长度摆长实验测出的周期，通过公式

(13)

计算得到此次实验装置摆长测得的周期的A类不确定度为0.000 086 9 s，式中n=4.

示波器标注误差为±0.01%，因此根据公式：

(14)

得到周期的B类不确定度为0.000 057 735 s.

(4)合成不确定度

将上述不确定度进行A类和B类不确定度合成，有

(15)

(16)

其中ΔT为取值范围误差.

根据公式(3)可知，g与(L+R)和T之间的关系是乘除关系，因此可根据公式：

(17)

(18)

计算间接测量重力加速度的不确定度，得到此次测量实验不确定度为0.010 1 m/s2，如图4所示.

5 结论与展望

本文首次提出将传统的单摆法和电磁感应原理相结合的设计思路，用以精确测量本地重力加速度.在测量电路之中加入了滤波器模块，使得实验现象清晰可见，实现了单摆周期的“可视化”.这一点是其它实验方案所不具备的.所以，本文的设计方案不仅有利于实验者，特别是学生，了解简谐振动和周期的特点，还可以促使学生认识电磁感应现象.通过对阻尼的分析和实验验证，可以进一步促使学生更深入的思考电磁相互作用.在测量过程中使用示波器记录实验信号，可以促使学生掌握基本科研仪器的使用方法和技巧等.

本设计存在可以改进的地方，比如，在摆线长度的测量方面，本实验是在悬挂状态下使用米尺测量，这种方式存在一定的人为误差，而且不便于估计.虽然本文认为摆长的不确定度很小，但是笔者期待更可靠的方法实现摆长的可靠测量.