利用拉格朗日量求解黑洞背景下自由光子的运动

魏少文，付春娥

(1.兰州大学 物理科学与技术学院力学基础教研室，甘肃 兰州 730000; 2.西安交通大学 物理学院应用物理系，陕西 西安 710049)

我们假设光子在一球对称史瓦西黑洞背景下自由运动，那么这一光子有可能逃离黑洞，也有可能被黑洞吸收.在弯曲时空中，光子具体的运动是由测地线方程来决定的，因此可以通过求解测地线方程来获得光子的运动及其轨迹.然而基于时空的对称性，我们也可以借助于自由光子的拉格朗日量来求解光子的运动.这一方法比直接求解测地线方程更简洁，同时也可以作为理论力学教学中的一个典型习题.本文将要讨论的是，如何利用拉格朗日量求解黑洞背景下光子的运动，进一步结合有效势能的概念，确定光子可能的运动范围，最终根据力学中运动学反问题得到光子的运动轨迹.

1 黑洞背景下光子的拉格朗日量及其运动

史瓦西黑洞由下述时空线元描述：

(1)

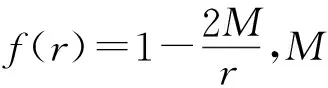
(2)

选取4个坐标为广义坐标，在此弯曲的黑洞背景下自由光子的拉格朗日量可以表述为[1]

(3)

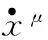
(4)

由于该时空的对称性，我们知道光子的能量E和角动量l守恒，即有p1=-E和p4=l.对具体的分量有

(5)

(6)

(7)

由于光子在赤道面上运动，因此p3=0.另外由于光子的静止质量为零，因此其拉格朗日量L=0.结合拉格朗日量式(3)，我们容易得到自由光子在黑洞背景下的4速度为

(8)

(9)

(10)

(11)

此即自由光子在球对称史瓦西黑洞背景下的坐标4速度，进一步对此做积分就可以得到光子的运动情况.“±”表示光子沿着径向向外或向内运动.

2 径向运动和有效势

这里我们只关心光子沿径向的运动.式(9)可改写为

(12)

由于经典力学中动能正比于速度的平方，所以第1项可以看成是动能项，第2项为有效势能项，即

(13)

因此式(12)完全类似于机械能守恒[3].那么可以通过对有效势的分析得到光子在径向上运动的范围及相应的性质.由式(13)，我们可知在黑洞视界面处和径向无穷远处，有效势具有如下行为

Veff|r=2M=0

(14)

Veff|r→∞=0

(15)

因此有效势具有一个单峰结构，且位于r=3M.我们在图1中画出了有效势随径向r的行为变化.根据力学中关于机械能守恒的章节内容，我们知道，由于动能非负，所以允许光子运动的区域满足

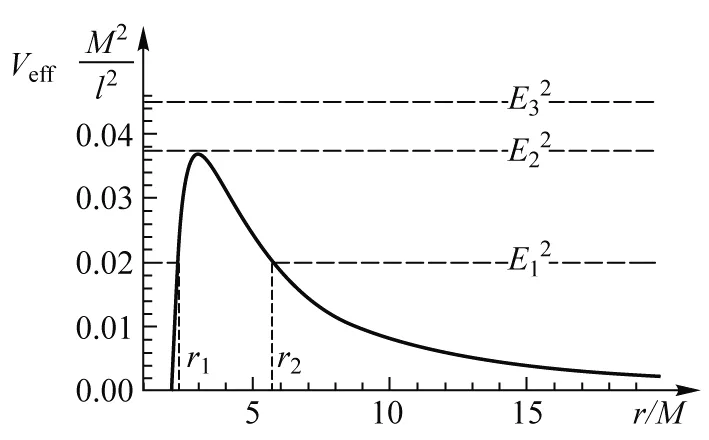
图1 光子在黑洞背景下的有效势

E2≥Veff

(16)

根据这一要求，我们分3种典型情况讨论光子可能的运动区域：

3 运动学反问题和运动轨迹

接下来我们将利用光子的4速度计算光子在赤道面内的运动轨迹.这一问题刚好是力学中的运动学反问题，即指已知速度或加速度求物体位矢的问题.

根据运动学反问题知识，如已知物体的速度v，求解其位矢r需要对其速度进行一次积分，即

(17)

这一不定积分的计算会出现一个积分常量(常矢量)，它代表物体最初的初位矢.

因此，要从4速度得到光子的运动轨迹，必须先给定光子的初位置.据此，我们假设光子初始时位于(r,φ)=(10M,0)并射向黑洞.那么对式(9)和式(11)进行积分，我们就可以得到光子运动轨迹.

取光子的能量分别等于E1、E2和E3时，我们通过数值计算获得了光子在赤道面上的运动轨迹，如图2所示.

图2 不同能量的光子在黑洞背景下的运动轨迹(黑色区域代表黑洞)

当光子能量为E1时，可以看到光子从初位置入射后逃离黑洞.当能量为E2时，光子从初位置入射后，抵达圆形轨道，并在此轨道上绕黑洞做圆周运动.当光子能量为E3时，光子从初位置出发后，很快被黑洞吸收.这完全符合由有效势分析的结果.

4 总结与讨论

本文利用拉格朗日量成功求解了黑洞背景下自由光子的运动这一问题.在具体的求解过程中，有机地结合了力学和理论力学中的拉格朗日量、机械能守恒、有效势和运动学反问题等多个知识点.通过此问题的求解，可以帮助我们灵活运用知识，将力学和理论力学中的知识应用到前沿的课题研究中.有质量粒子的轨道分类看参考文献[5].