一维j原子链晶格振动的色散关系

郑世燕，袁怡圃，常斗亮

(泉州师范学院 物理与信息工程学院，福建 泉州 362000)

晶格振动是指晶体中的原子在其平衡位置附近作微振动.而色散关系是晶格振动理论研究重点之一.只有深入地了解了晶格振动的色散关系，晶体的许多性质才能得到理解，它是研究固体宏观性质和微观过程的重要理论基础.现有的“固体物理学”教材[1-5]中多数是在简谐和最近邻双重近似条件下分析一维单原子链和双原子链晶格振动模型的色散关系，它们是学习晶格振动色散关系的两个非常经典的例子，它们的振动既简单可解，又能较全面地表现出色散关系的基本特点.

在此基础上，有学者[6,7]进一步分析了一维三原子链晶格振动模型的色散关系，该振动依旧可获得解析解.笔者不禁要问：一维四原子、五原子甚至更多原子组成的原子链晶格振动模型的色散关系是否依然可获得解析解？本文将以一维j原子链晶格振动模型为研究对象，并在简谐和最近邻双重近似条件下试图获得一维j原子链晶格振动方程组的一般表达式.现有教材[1-5]及文献[6,7]中的一维单原子、双原子以及三原子链的色散关系亦可由该一般表达式简化获得.最后通过数值模拟分析法重点对一维四原子链晶格振动的色散关系进行分析讨论，并指出由更多原子组成的原子链亦可由本文所获得的晶格振动方程组获得其相关规律.

1 一维j原子链晶格振动模型

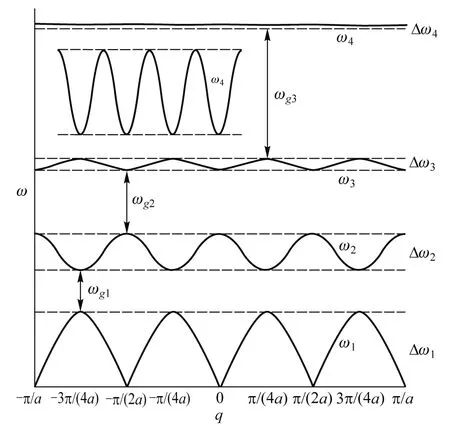
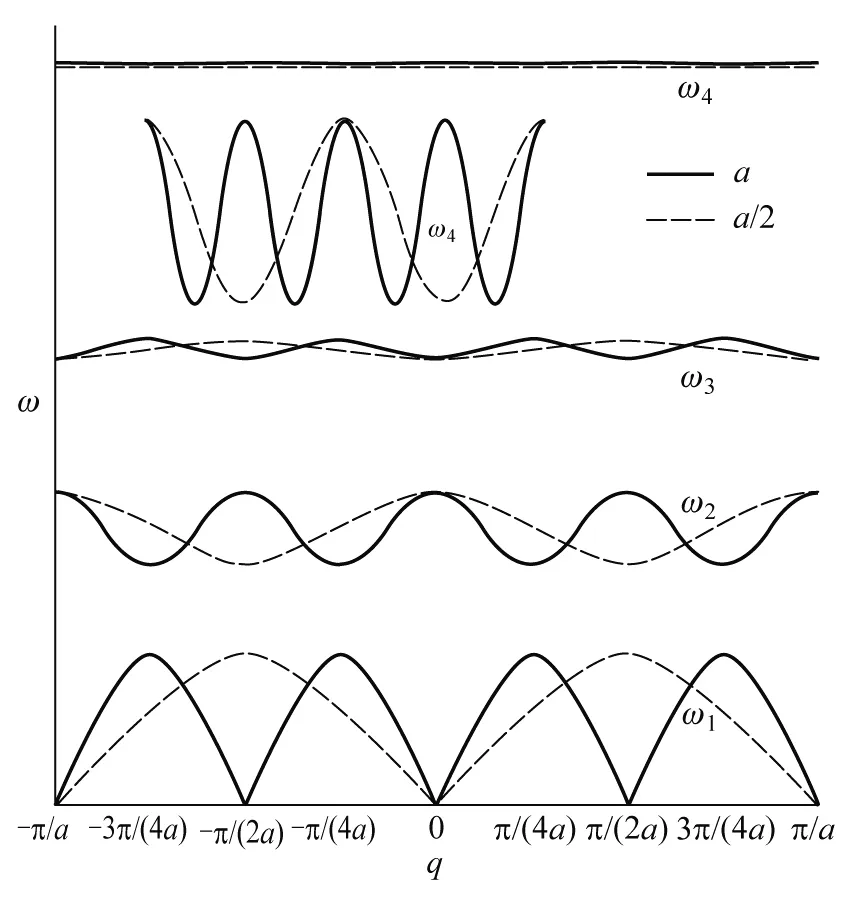
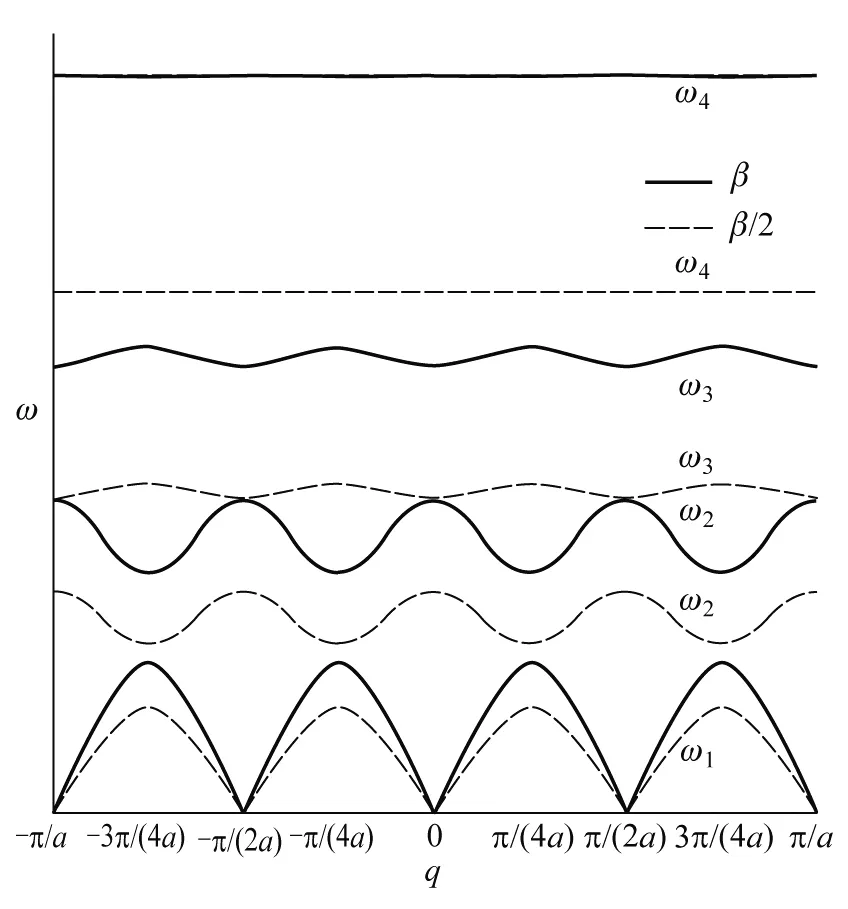
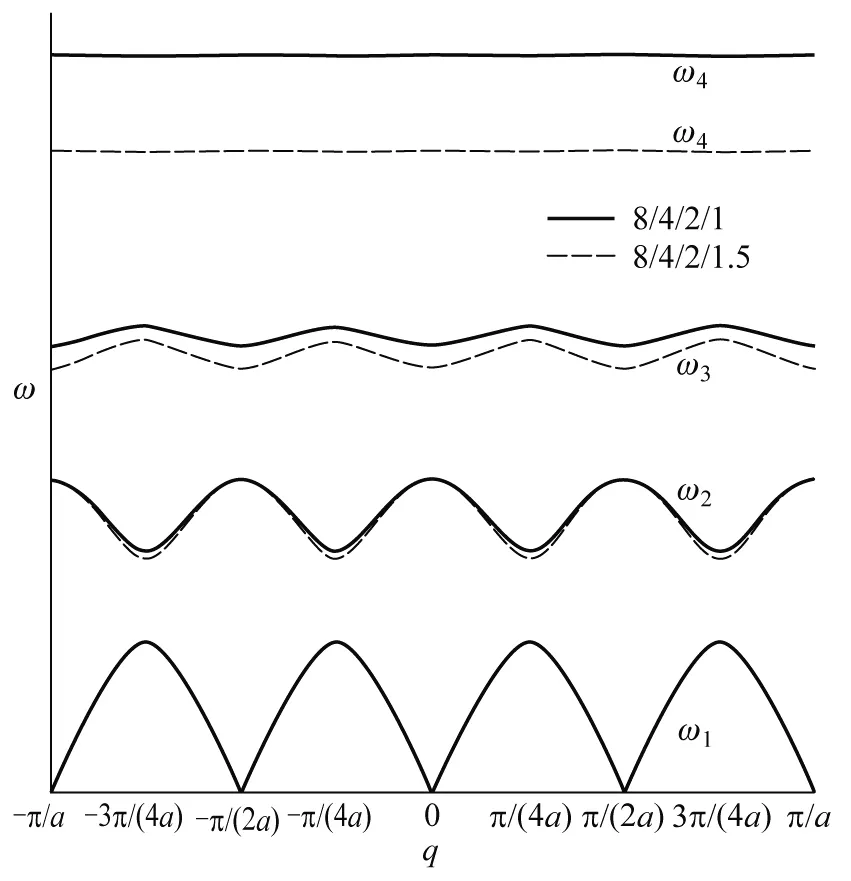
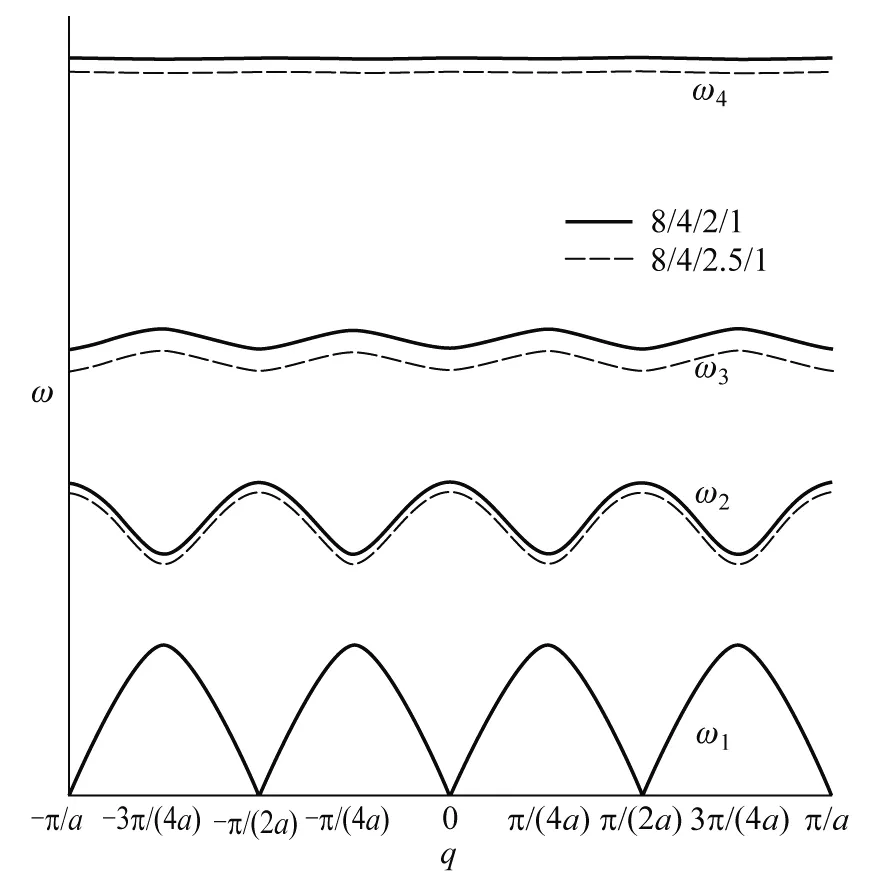
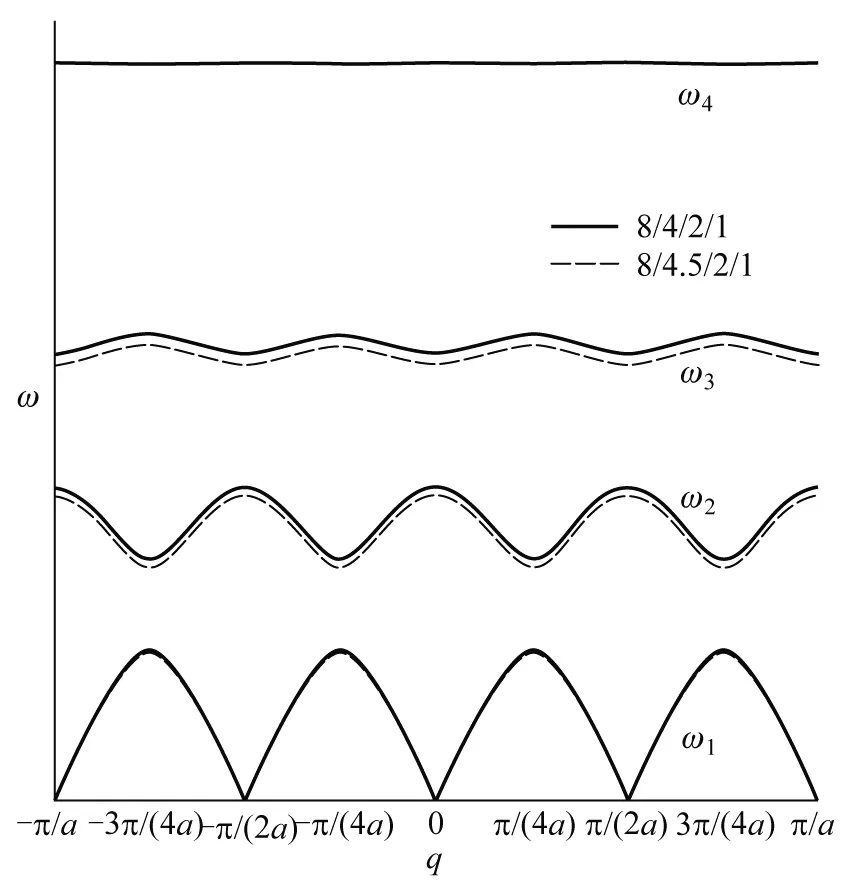
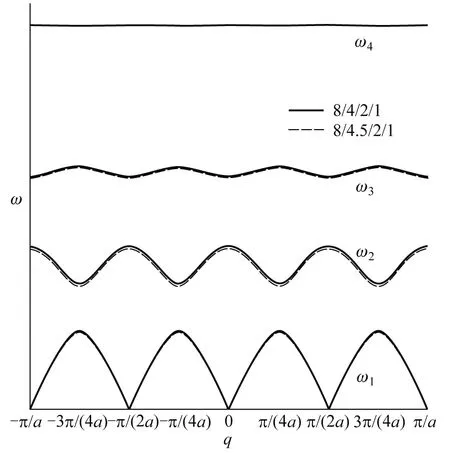
质量分别为m0、m1、m2、…、mj-1(m0

图1 一维j原子链晶格振动模型示意图

为方便计算，本文仅考虑简谐运动下最近邻原子间的相互作用，且在任意相邻原子间相互作用的恢复力系数都相等的情况下，进一步根据经典牛顿力学理论获得一维j原子链原胞内j个不同原子运动方程分别为

(1-1)

(1-2)

(1-3)

…………

(1-j)

易知方程组(1)为二阶微分方程组，它们有许多形式的解，考虑各原子的振幅分别为A0、A1、A2、…、Aj-1，做频率相同(设为ω)的简谐振动时，其离开平衡位置的位移分别为

μjn=A0ei(qjna-ωt)

(2-1)

μjn+1=A1ei[q(jn+1)a-ωt]

(2-2)

μjn+2=A2ei[q(jn+2)a-ωt]

(2-3)

…………

μjn+(j-1)=Aj-1ei{q[jn+(j-1)]a-ωt}

(2-j)

并把方程组(2)代回方程组(1)得到关于振幅A0、A1、A2、…、Aj-1的齐次线性方程组：

Aj-1βe-iqa+A0(m0ω2-2β)+A1βeiqa=0

(3-1)

A0βe-iqa+A1(m1ω2-2β)+A2βeiqa=0

(3-2)

A1βe-iqa+A2(m2ω2-2β)+A3βeiqa=0

(3-3)

…………

Aj-2βe-iqa+Aj-1(mj-1ω2-2β)+A0βeiqa=0

(3-j)

再按振幅A0、A1、A2、…、Aj-1的顺序重新改写上述齐次线性方程组如下：

A0(m0ω2-2β)+A1βeiqa+A2·0+

A3·0+…+Aj-2·0+Aj-1βe-iqa=0

(4-1)

A0βe-iqa+A1(m1ω2-2β)+A2βeiqa+

A3·0+…+Aj-2·0+Aj-1·0=0

(4-2)

A0·0+A1βe-iqa+A2(m2ω2-2β)+A3βeiqa+

A4·0+…+Aj-1·0=0

(4-3)

…………

A0βeiqa+A1·0+A2·0+…+Aj-1·0+

Aj-2βe-iqa+Aj-1(mj-1ω2-2β)=0

(4-j)

方程组(4)由j个方程所组成，即为一维j原子链晶格振动方程组的一般表达式.换言之，当j=1时，方程组(4)只有式(4-1)；当j=2时，方程组(4)由式(4-1)和式(4-2)所组成；当j=3时，方程组(4)由式(4-1)、式(4-2)和式(4-3)共同组成；以此类推……

接下来将基于方程组(4)，从中分别获取一维单原子、双原子、三原子、四原子等原子链的色散关系.

2 特例

2.1 一维单原子链(j =1)晶格振动

当j=1时，上述一维j原子链简化为一维单原子链情形，此时只有一个系数A0，满足式(4-1).这时还需令式(4-1)中的A1=A0，且其他系数A2、A3、A4、…都为零.则当系数A0有非零解时，式(4-1)简化为如下色散关系:

(5)

这与现有教材[1-5]中所获得的结论相吻合，即由完全相同原子所组成的一维单原子链的晶格振动只有声学波.

2.2 一维双原子链(j=2)晶格振动

当j=2时，对应双原子链，此时有两个系数A0和A1，满足式(4-1)与式(4-2).令式(4-1)与式(4-2)中的A2=A0，且其他系数都为零.则当系数A0和A1有非零解时，式(4-1)与式(4-2)简化为如下色散关系：

(6)

式(6)为二阶行列式，它是关于ω2的一元二次方程，易求得其色散关系为

(7)

其中ω±代表晶格振动中声频支与光频支格波的频率，即声学波的频率为ω-而光学波的频率为ω+.这也与现有教材[1-5]中所获得的结论相符，即一维双原子链晶格振动可以存在2种独立的格波(声学波ω-和光学波ω+).

2.3 一维三原子链(j =3)晶格振动

当j=3时，对应三原子链，此时有三个系数A0、A1和A2，满足式(4-1)、式(4-2)与式(4-3).令式(4-1)、式(4-2)与式(4-3)中的A3=A0，且其他系数都为零.则当系数A0、A1和A2有非零解时，式(4-1)、式(4-2)与式(4-3)简化为如下色散关系

(8)

式(8)为三阶行列式，它是关于ω2的一元三次方程，亦可根据数学上一元三次方程的求根公式获得其色散关系的解析表达式[6,7]，从而知晓一维三原子链的色散关系由声学波、低频光学波和高频光学波这3种独立的格波组成.

2.4 一维四原子链(j =4)晶格振动

当j=4时，对应四原子链，此时有四个系数A0、A1、A2和A3，其色散关系应满足

(9)

式(9)为四阶行列式，它是关于ω2的一元四次方程，求其解析解较繁琐，之后将考虑用数值解的方法讨论其色散关系.不难推测，一维四原子链的色散关系应由4种独立的格波组成.

2.5 一维j原子链(j ≥5)晶格振动

以此类推，当j≥5时，此时应有j个系数A0、A1、A2、…、Aj-1，其色散关系可用j阶行列式来描述，即

(10)

式(10)为关于ω2的一元j次方程，该色散关系应由j种独立的格波组成.但当j≥5时，求其解析解相对困难，此时数值解显得尤为重要，因它可直观地给出具体图像，为分析研究一维原子链晶格振动特点提供一定的理论及图像依据.

为深入了解一维j原子链晶格振动的特点，本文将以目前未曾报道过的一维四原子链晶格振动为例分析其色散关系.

3 一维四原子链晶格振动的数值模拟分析

一维四原子链晶格振动的色散关系由式(9)所决定，它与原子间距a、恢复力系数β以及4个原子质量(m0、m1、m2和m3)均有关系.应用MATLAB软件对式(9)进行数值模拟分析，可得一维四原子链晶格振动的色散关系曲线.该色散关系由4条曲线所构成，如图2所示.图中ω1、ω2、ω3和ω4分别表示声学波、低频光学波、中频光学波和高频光学波所对应的频率；Δω1、Δω2、Δω3和Δω4分别表示声学波、低频光学波、中频光学波和高频光学波的频谱宽度；ωg1、ωg2和ωg3分别表示声学波与低频光学波间、低中频光学波间以及中高频光学波间的频率禁带宽度.另外，由于高频光学波的色散关系曲线相较于声学波、低频光学波以及中频光学波所对应的色散关系曲线变化较不明显，故在图2左上角内插图中显示了高频光学波的色散关系曲线放大图.

图2 一维四原子链色散关系曲线

3.1 原子间距对晶格振动的影响

在原子质量(m0、m1、m2和m3)与恢复力系数(β)保持不变的情况下，令式(9)中的原子间距分别为a和a/2，其色散关系曲线如图3所示，图中左上角内插图中显示了高频光学波的色散关系曲线放大图.分析图3曲线可知：

图3 不同原子间距下一维四原子链色散关系曲线

2)在简约布里渊区范围内，观察图3曲线的斜率变化可知，曲线斜率随着原子间距的减小而减小，意味着晶格振动在晶体中的传播速度(即格波速度)随原子间距的减小而减小，由此进一步说明格波速度与晶格结构的周期性有关.

3)频谱宽度(Δω1、Δω2、Δω3和Δω4)和频率禁带宽度(ωg1、ωg2和ωg3)并未受到原子间距变化的影响，说明频谱宽度和频率禁带宽度与晶体结构的周期性无关.

3.2 恢复力系数对晶格振动的影响

在原子间距(a)与原子质量(m0、m1、m2和m3)保持不变的情况下，令式(9)中的恢复力系数分别为β和β/2，其色散关系曲线如图4所示，分析图4曲线可知：

图4 不同恢复力系数下一维四原子链色散关系曲线

1)简约布里渊区宽度并不随恢复力系数的变化而变化，说明简约布里渊区宽度与恢复力系数无关.

2)曲线斜率除了声学波ω1随着恢复力系数的减小而变小外，低频光学波ω2、中频光学波ω3和高频光学波ω4曲线斜率变化较不明显，即声学波波速有所减小而光学波波速变化不大，由此说明恢复力系数对声学波的波速影响较明显.

3)随着恢复力系数的减小，4种格波的频率值相应减小，频谱宽度和频率禁带宽度都有变窄趋势，由此说明带通滤波器的设计应考虑恢复力系数变化对频谱宽度和频率禁带宽度的影响.

3.3 原子质量对晶格振动的影响

如前所述，对于一维四原子链，原胞内共有4个不同的原子，质量分别为m0、m1、m2和m3.为分别分析每种原子变化对晶格振动的影响，将在原子间距(a)及恢复力系数(β)保持不变的情况下，每次只改变4个原子质量中的一个进行数值模拟分析获得其色散关系曲线.即在原子质量比为m3/m2/m1/m0=8/4/2/1的基础上，分别再取m3/m2/m1/m0=8/4/2/1.5、8/4/2.5/1、8/4.5/2/1、8.5/4/2/1.其色散关系曲线如图5、图6、图7及图8所示，综合分析图5、图6、图7及图8曲线可知：

图5 不同m0下一维四原子链色散关系曲线

图6 不同m1下一维四原子链色散关系曲线

图7 不同m2下一维四原子链色散关系曲线

图8 不同m3下一维四原子链色散关系曲线

1)简约布里渊区宽度也不随着原子质量的变化而变化，说明简约布里渊区宽度与原子质量无关.

2)原子质量对4种格波的频率值均有影响，只是对声学波的影响较小，而对光学波的影响较大.体现在：当m0或m1改变时，中高频光学波频率值变化较明显；当m2改变时，低中频光学波频率值变化也明显；但m3对所有格波的影响都较不明显.

3)原子质量对4种格波的频谱宽度影响较小，而对频率禁带宽度的影响较大.特别地，当m0或m1改变时，低中频光学波间以及中高频光学波间的频率禁带宽度ωg2与ωg3变化较明显.该结论对工程实际应用中带通滤波器的设计可提供一定的理论参考价值.

4 结论

本文紧密围绕简谐及最近邻双重近似条件下所获得的一维j原子链晶格振动方程组的一般表达式，对其进行数值模拟分析.具体以一维四原子链晶格振动为例分析了其色散关系，并进一步探讨了原子间距、恢复力系数及原子质量等晶体结构参数对晶格振动的影响.结果表明：改变正空间中的原子间距直接影响了倒空间中的简约布里渊区宽度，即随着原子间距的增大简约布里渊区宽度按照反比例减小；随着恢复力系数的减小，引起了格波频率值减小、频谱宽度和频率禁带变窄；原胞内4种原子质量的变化对4种格波的频谱宽度、频率禁带均有影响.

简言之，本文所述内容不仅可推出现有固体物理学教材及文献中已有的一些重要内容，而且还可以推导出一些有意义的新结论.表明本文所获得的结果具有一般性，它对带通滤波器的设计可提供一定的理论参考价值.