数字正射影像平面精度分析

何军利

（山西省测绘地理信息院,山西 太原 030001）

0.引言

数字正射影像图具有固定的比例尺和一定的平面精度，由于其信息丰富、直观、方便使用等特点，被广泛地应用于自然资源调查、水力资源调查、地理国情监测等领域。由于DOM的生产由专业技术人员完成，且应用部门大多是直接使用DOM，对DOM的生产过程并不了解，故很难全面正确理解DOM的平面精度。在实际生产中，经常会出现很多误区，如认为DOM的精度很高，可以用来提取地理信息数据；当部分地理信息数据与DOM套合偏差较大时，无法判定是影像还是地理信息数据出现了错误；部分专业从事质量检验的技术人员对正射影像图的精度认识也存在误区，无法准确判定正射影像平面精度是否符合规范要求。本文通过对常用比例尺数字正射影像生产过程的分析，明确阐述正射影像图存在平面误差的大小及形式，重点介绍了投影误差和比例误差，并对其产生的原因、大小、方向进行了定量分析。同时给出了改正误差的方法，对正射影像的正确应用及质量检查可起到一定的指导作用。

1.数字正射影像存在的误差及大小分析

数字正射影像图是以航摄影像或遥感影像为基础，经过逐像元进行辐射改正、微分纠正和镶嵌，按地形图规范裁切形成的影像数据成果。数字正射影像存在的系统误差主要有空三加密造成的系统误差（整体的或某一区域的）、影像偏离投影中心产生的投影误差、数字高程模型错误产生的比例误差等，其中合格的空三加密造成的系统误差一般很小，而影像的投影差和比例误差却大量存在，对成果质量影响较大。

1.1 数字高程模型错误引起的比例误差

数字高程模型（DEM）引起的比例误差，主要是由于影像纠正使用的是数字地面高程模型，没有考虑地面建筑物高度，建筑物在纠正时存在很大误差。本文定义此类误差为比例误差（如图1所示）。M为比例误差，CDEF为地面建筑物垂直截面图，CD=EF=L0、CD在像平面对应ab=L、相对航高H、建筑物高度h、航摄相机焦距f、比例误差定义为M，则比例误差M=L0×（H/（H-h）-1）=L0×（h/（H-h））。式中虽然没有航摄焦距f,但航摄时相对航高的选取与相机焦距有直接关系，相对航高=（相机焦距×地面分辨率）/像元尺寸，获取一定分辨率的航摄影像，焦距越小、相对航高越小，焦距越大则航高越大。

图1 比例误差示意图

以中心式投影成像方式显示的比例误差（如图1所示），显示建筑物比例误差的大小与建筑高度和摄影的相对航高有关，与建筑物和投影中心的位置无关。在ADS80或ADS100等推扫式成像的正射影像生产时比例误差依然和相对航高、建筑物的高度有关，本文没有将此作为重点内容进行论述。

依据目前摄影测量生产项目的实际情况，笔者对常见比例尺数字正射影像图存在的比例误差进行统计分析（表1为以边长为50m的建筑为样本的统计结果）。通过对样本数据分析发现：1∶10000数字正射影像的生产模式中比例误差的大小基本在限差以内；1∶2000数字正射影像上高层建筑（20层以上）比例误差会超限；1∶500及1∶1000数字正射影像图上的建筑比例误差都会超过限差，使用相机焦距越小，相对航高越小，比例误差越大。

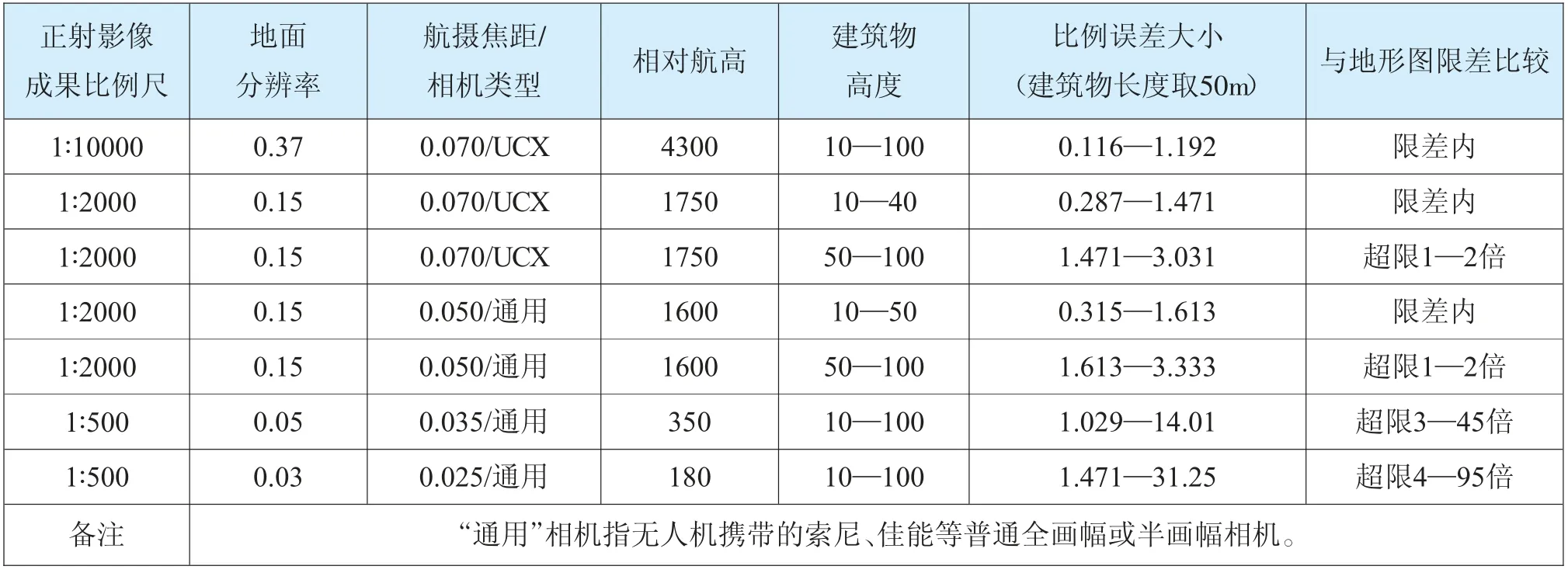
表1 数字正射影像比例误差大小样例分析 单位：m

结论：比例误差的大小和建筑物长度成正比，和建筑物高度成正比，和相对航高成反比。

1.2 建筑物偏移投影中心产生的投影误差

建筑物偏移投影中心产生的投影误差：以中心投影的正射影像纠正作为定义的参考（如图2所示），其中航摄项目相对航高为H1、航摄相机焦距为f、建筑物的高度为h0、建筑物离开投影中心的距离为D1。高层建筑在偏离投影中心时，将产生投影中心与建筑物连线延长线方向的平面位置偏移，本文将一定高度的建筑物偏离投影中心产生的正射影像纠正误差称为投影误差(图2中D2-D1大小)。

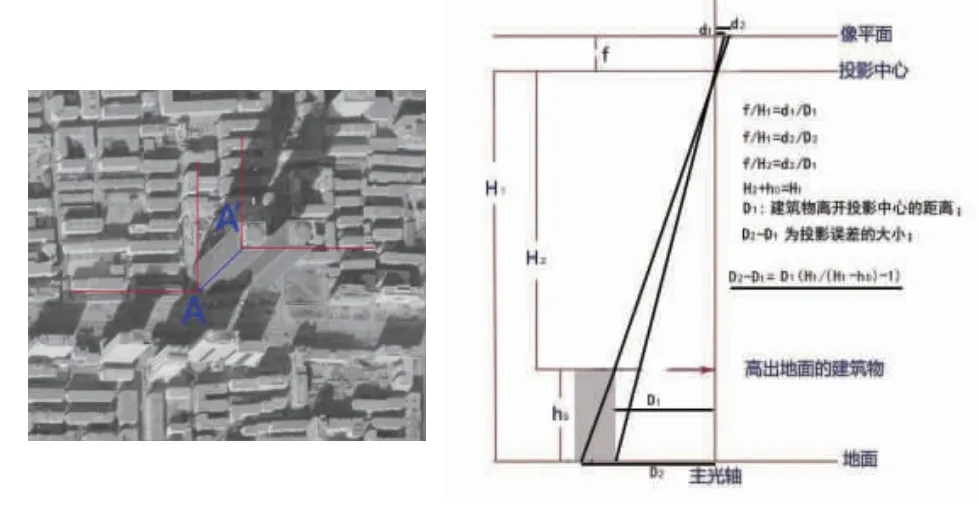
图2 中心投影误差示意图

故：投影误差=D1(H1/(H1-h0)-1)

投影误差分布特点分析：以利用单张影像的外方位元素和数字高程模型进行数字微分纠正得到的数字正射影像，投影误差分布特点是：距离投影中心距离越远，投影误差越大；航摄时航向和旁向重叠度越小，相机幅面越大，则对应建筑物距离投影中心的距离会越大，投影误差也越大；建筑物的高度越高，投影误差越大；航摄时的相对航高越大，投影误差越小。由于成图比例尺确定以后，航摄的地面分辨率也是确定的，此时相对航高的大小取决于相机的焦距，焦距越长相对航高越大。因此相机焦距越大，则相对航高越大，影像投影误差越小。

投影误差平面位移方向是投影中心与建筑物连线的延长线方向。对一定高度建筑的平面位置（离开投影中心的距离和方向）和投影误差的大小制作误差分布图。中心式投影方式成像的投影误差分布（如图3所示），影像四角误差最大；推扫式成像的投影误差分布（如图4所示）：

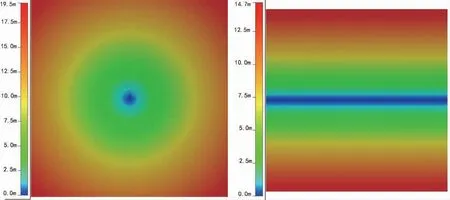
图3 中心投影RC30相机为例

图4 以ADS80相机为例

从图3可以看出，中心式成像的航空影像生产数字正射影像图投影误差在影像中心位置最小，邻近四角处误差最大；从图4可以看出，ADS40、ADS80系列推扫式相机生产的数字正射影像图，在带状影像的中心线位置投影误差最小，航线边沿处误差最大，随着新的ADS100相机的推出，影像宽度从18000个像素提升到22000个像素，ADS100的航线覆盖宽度变大，正射影像纠正时航带边缘的投影差更大。

正射影像投影差的大小到底有多大，从公式上我们很难有直观的感受，现在我们针对第一代数字正射影像常用的RC10相机为例，进行投影误差的大小进行分析。假定采用RC10相机进行航摄，设定焦距为153mm，相机幅面为23cm×23cm，生产1∶10000、1∶2000、1∶500的数字正射影像，航向重叠度为65%、旁向重叠度为35%，计算像点在航线上和垂直航线的旁向上最大投影差L1，像点位于对角线方向的最大投影差L2。选取不同高度的地物计算投影差大小统计情况（如表2所示）：

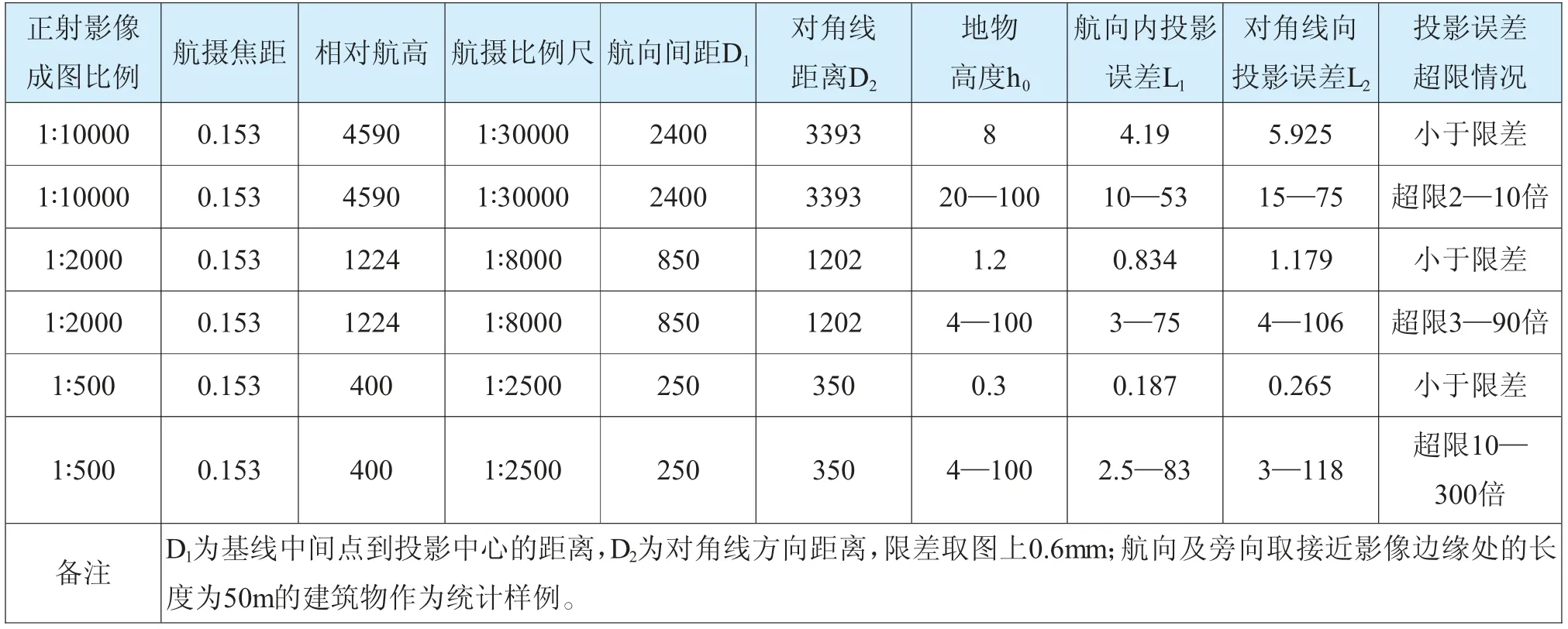
表2 以RC10传统相机为例的数字正射影像 单位：m

从表2可以看出，当相机选定后，在1∶10000比例尺的正射影像上8m以下的地物投影差不会超限；在1∶2000比例尺的正射影像上1.2m以下的地物投影差不会超限，实际生产中绝大多数房屋的投影差都会超限；在1∶500比例尺的正射影像上0.3m以下的地物投影差不会超限，这样常见的建筑物投影误差都会严重超限，正射影像比例尺越大，投影误差越大。

随着数码航摄相机的出现，传统RC30相机逐渐被淘汰，在大量数字摄影测量项目中，开始以ADS80、DMC、UCX等相机为主进行航摄，表3以UCX相机为例对其生产的常见比例尺数字正射影像存在的投影误差进行分析。近年来随着无人机技术飞速发展，越来越多的航空摄影测绘项目开始使用无人机进行1∶2000、1∶1000、1∶500比例尺的数字正射影像图的生产。表4以目前常用无人机搭载50mm、35mm、25mm焦距的普通相机为例，计算其生产的数字正射影像图的投影误差大小。可以发现城市建筑物的投影误差都非常大，正射影像上的建筑物平面位置误差很大，平面位置参考价值不大。

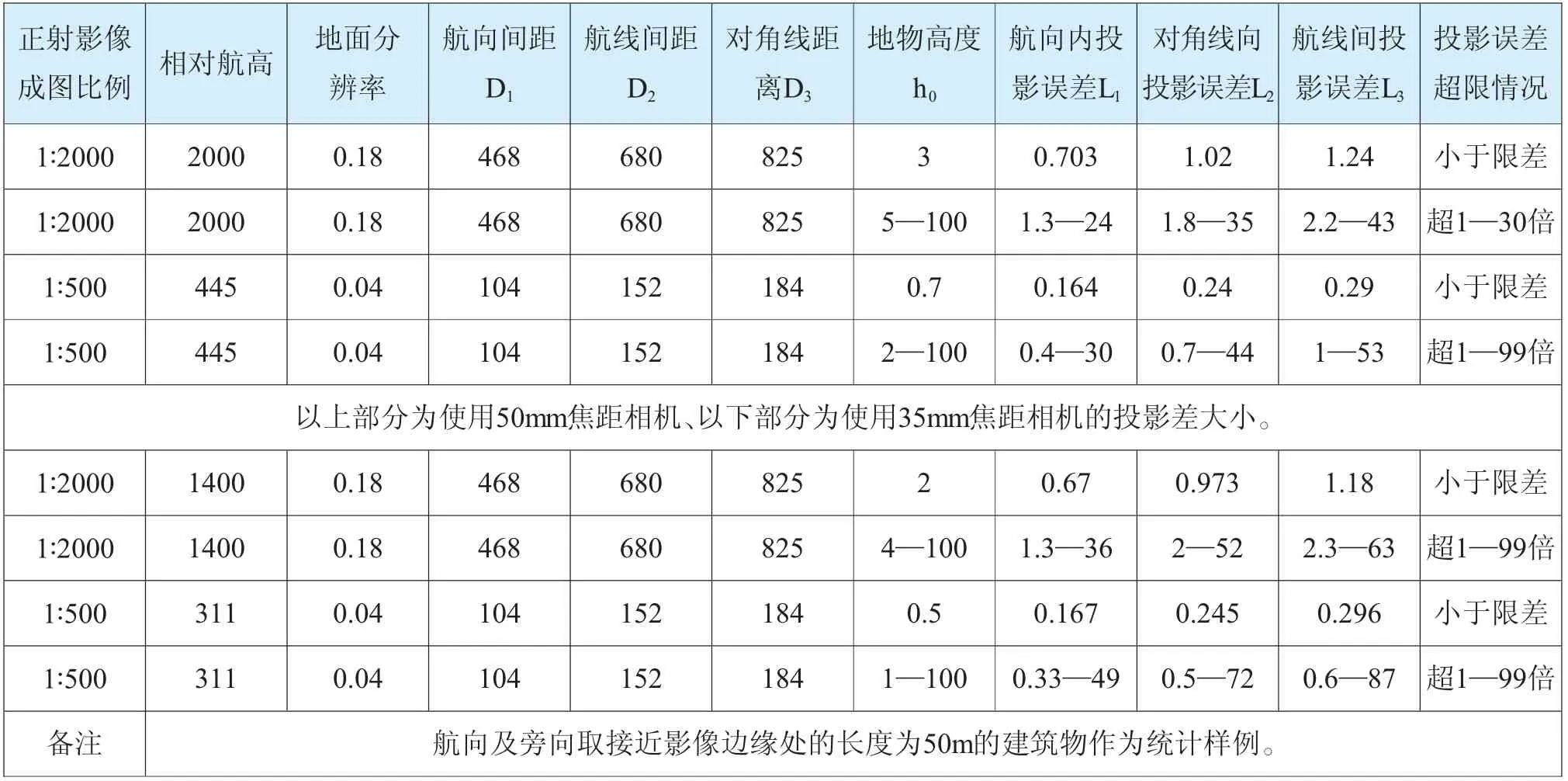
表4 普通无人机相机为例的数字正身影像 单位：m

结果分析：数字正射影像的比例误差和中心投影误差是同时出现，且相互叠加增大的；目前的数字正射影像产品中，1∶10000比例尺的正射影像精度较好，1∶2000比例尺的数字正射影像如果采用大飞机、长焦相机进行航摄生产非主要城市区域的，平面精度也可以满足要求，但1∶1000、1∶500比例尺的数字正射影像的城市地区，地物（建筑物）平面精度都严重超限，平面位置没有参考价值。

2.减小正射影像比例误差和投影误差的方法

2.1 选取适当的航摄相机

从比例误差和投影误差的公式可以发现，误差的大小和相对航高成反比，获取一定分辨率的影像，相对航高的大小取决于航摄像机的焦距，相机焦距越长相对航高越大，比例误差和投影误差越小。生产项目如果只是获取正射影像成果，则优选长焦相机进行航空摄影。

2.2 选取适当的航向和旁向重叠度

当相机选定以后，为了尽量减小比例误差和投影误差，正射影像的生产需要考虑航摄的航向和旁向重叠度，航向和旁向重叠度越大，建筑物离开投影中心的距离会减小，投影误差会减小，但是会增加航摄成本并增加数据处理工作量。综合分析，数字正射影像生产项目航摄时应加大航向重叠度，并适当增加旁向重叠度，如航向重叠度75%—85%、旁向重叠度35%—45%为最佳。

2.3 生产数字真正射影像

对于大比例尺（1∶2000、1∶1000、1∶500）数字正射影像生产，技术上无论如何改进，比例误差和投影误差依然会严重超限，这时候生产工艺应改为航摄时使用正射大重叠度（航向85%、旁向60%）“十字”构架敷设航线，或利用多拼倾斜相机摄影来生产数字真正射影像，彻底消除两类误差，提高影像底图的平面精度。

3.结束语

随着无人机、倾斜摄影、影像智能匹配、计算机集群计算等技术的发展，目前已经支持1∶2000、1∶1000、1∶500等大比例尺数字正射影像生产技术的全面升级，以消除正射影像上的比例误差和投影误差，提升影像图的平面精度，实现正射影像和地形图的平面精度趋于一致。随着卫星影像获取、全数字摄影测量软件、影像智能匹配等技术的进一步发展，未来摄影测量技术会实现进一步的升级，可以利用卫星影像、ADS100影像、多视倾斜相机影像生产1∶10000、1∶2000比例尺的数字真正射影像，并得到更广泛的应用。