三相桥式变流器负序电流补偿策略

周丽莹 ，夏昌浩 ，2

（1.三峡大学电气与新能源学院，湖北 宜昌 443002；2.湖北省微电网工程技术研究中心（三峡大学），湖北 宜昌 443002）

中低压配电网中无功、负序等负荷潮流往往相互耦合且不断剧烈变化，导致电网功率因数偏低、电压闪变、三相电压不平衡等多种电能质量问题，引起电网损耗和设备损坏，严重影响电力系统经济稳定运行[1-2]。安装在公共连接点（point of common coupling，PCC）附近的有源电力滤波器（active power filter，APF）、静止同步补偿器（static synchronous compensator，STATCOM）等并联补偿设备和光伏逆变器等分布式电源设备，通过瞬时无功功率等方法检测提取其中的无功、负序潮流，可对其进行综合补偿[3-4]，相较于无源补偿设备，控制方式更加灵活，响应速度更快[5]。然而，受限于电力电子设备的高昂造价，在实际应用中，安装容量通常不足以完全补偿无功和负序电流[6]。

国内外学者针对有限容量并联补偿器的电能质量补偿问题，提出诸多解决和改善方法。文献[7-8]提出将光伏并网逆变器等用于电能质量治理，以缓解并联补偿设备容量不足的状况，文献[9]研究了兼具阻抗重塑、电能质量治理功能的并网变流器拓扑及结构，文献[10-11]提出基于重复控制的多功能并网变流器，提高了对参考电流的跟踪效果和电能质量补偿效果。但是分布式电源并网逆变器首要功能为传输有功，有功容量接近额定容量时，其对电能质量影响有限。文献[12-13]提出低压配网多台STATCOM基于协调控制进行综合补偿的控制策略，但由于通信以及计算延时，实时响应无法保证。但上述文献都没有分析综合补偿时负序补偿电流相角对负序补偿效果的影响，STATCOM的容量潜力未得到充分利用。

为了提高有限容量并联补偿器的补偿效果，文献[14-15]针对铁路统一电能质量控制器，将负序补偿电流与负荷负序电流的相角差作为新的自由度，求解最优补偿解，提升负序补偿效果。并基于优化补偿策略提出固定补偿装置的铁道统一电能质量控制器容量综合配置方法；文献[16-17]针对牵引系统中V/v接线的牵引变电所，建立基于电压不平衡度、功率因数为约束条件的最优补偿数学模型，通过改进粒子群算法对问题进行求解。但以上优化补偿策略都不适应三相系统。因此有必要对三相系统无功负序综合补偿进行深入研究。

低压三相系统通常采用STATCOM等三相桥式变流器（three-phase bridge converter，TPBC）治理电能质量。本文针对有限容量的TPBC，提出优化综合补偿策略。在相平面上，优先确定无功补偿电流，通过TPBC桥臂电流约束，求得负序补偿电流可行域，通过解析几何的方法求解负序补偿电流最优解，提升负序补偿效果。最后Matlab的数值计算结果和PSCAD/EMTDC仿真结果都验证了所提优化综合补偿策略对TPBC补偿效果的提升。解析几何法计算量小，TPBC并不会由于增加了一部分优化计算而降低动态特性。

1 优化综合补偿分析与计算

1.1 优化综合补偿原理

以感性无功为例分析优化综合补偿的原理，如图1所示，相平面上闭合区域为TPBC负序补偿电流向量可行域。

图1 常规与优化补偿电流向量比较示意图Fig.1 Comparison diagram of conventional and optimized compensation current vector

图1中，向量OM代表负荷负序电流向量，点M在可行域外，不能被完全补偿；为常规策略下负序补偿电流向量，为常规综合补偿策略下负序补偿电流相位，为常规综合补偿下剩余负序电流向量；为优化综合补偿策略下负序补偿电流向量，为优化综合补偿策略下负序补偿电流相位，为优化综合补偿策略下剩余负序电流向量。

1.2 求解优化综合补偿最优解

传统的优化综合补偿数学模型比较复杂，其中还包含超越方程，无法通过求极值方法直接求解最优解。迭代法计算速度较慢，无法满足实时优化求解要求。本文以感性无功电流为例，提出解析几何与平面规划法求解最优补偿解。

图2为解析几何法求最优解示意图。

图2 解析几何法求最优解示意图Fig.2 Schematic diagram of optimal solution by analytic geometry

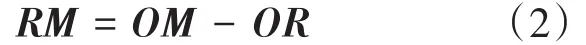
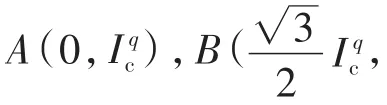
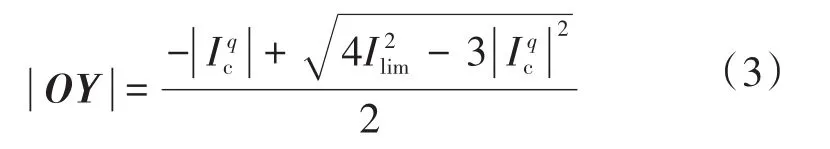
相平面上，目标点M（Ipn，Iqn）与A，B，C，X，Y，Z各点连线同横轴正方向的夹角为δA，δB，δC，δX，δY，δZ，Ipn与Iqn分别为有功、无功补偿电流值。可行域外的区域可由线CX，CY，BX，BZ，AZ，AY分割为图3所示六个部分。由6个夹角对目标点M所属区域进行判别，如表1所示。

表1 区域判据表Tab.1 Regional criterion table

图3 负荷负序向量分区示意图Fig.3 Diagram of load negative sequence vector partition

图3中，当目标点位于区域Ⅰ时，如图2所示点M1，AM1连线同圆A的交点即为所求最优解。可求出最优补偿解向量OR。当目标点位于区域Ⅱ时，如图2所示点M2，CM2连线与圆A交点在圆弧ZY的延长线上，AM2连线与圆C交点在圆弧XY延长线上，可求出最优补偿向量解。

同理，可解得各区域最优补偿向量解，如表2所示。

表2 各区域最优解Tab.2 Optimal solution for each region

1.3 优化综合补偿与常规综合补偿分析比较

两种综合补偿策略负序补偿电流相位如图4所示。实线表示常规综合补偿策略下负序补偿电流相位始终等于负荷负序电流相位；虚线表示优化综合补偿策略下负序补偿电流相位与的相角差周期性变化。

图4 负序补偿电流相位对比图Fig.4 Negative sequence compensation current phase comparison diagram

两种补偿策略效果下的负序剩余度如图5所示。

图5 负序电流负序剩余度对比图Fig.5 Negative sequence current negative sequence residuals comparison diagram

图5中，实线表示常规综合补偿策略下负序剩余度Kn_t，虚线表示优化综合补偿策略下负序剩余度Kn_o，如图5所示，除6个交点，优化综合补偿的下负序剩余度Kn_o都不同程度小于常规综合补偿下负序剩余度Kn_t。

为了综合评估优化综合补偿策略对补偿能力的提升效果，定义负序平均剩余度下降率TRNR满足下式：

图6为感性/容性无功补偿电流幅值标幺值Iq（pu）∈[0，1]，负荷负序电流标幺值In（pu）∈[0，2]负荷区间内TRNR的指标示意图。如图6所示，负序剩余度平均下降率与无功补偿电流幅值有关，Iq（pu）∈（0，1），且设备容量不足以完全补偿负序电流时，相较于传统补偿方式，优化综合补偿的负序平均剩余度均有不同程度下降。

图6 负序平均剩余度下降率TRNR示意图Fig.6 Diagram of negative sequence average residuals decreasing rate TRNR

2 无功、负序检测及TPBC控制

优化综合补偿策略控制框图如图7所示，包括电压锁相部分、直流侧电压控制部分、无功补偿电流计算部分和负序补偿电流部分。

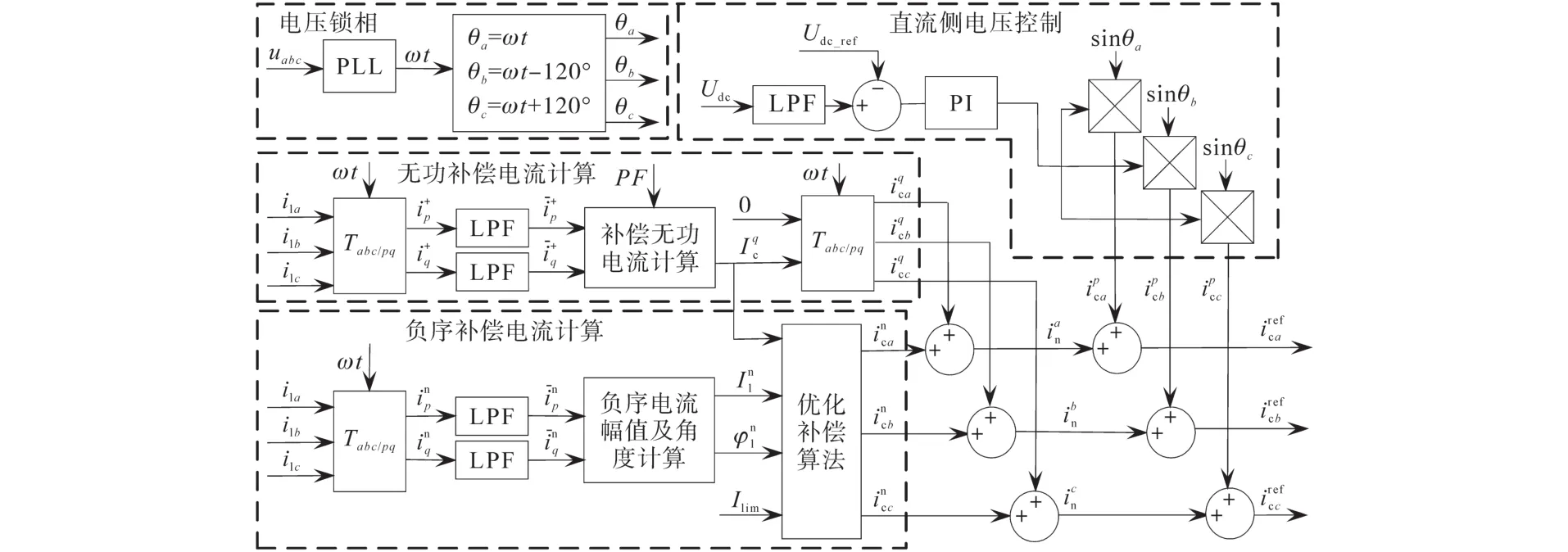
图7 三相桥变流器控制框图Fig.7 Three-phase bridge converter control block diagram

电压锁相部分通过PLL锁相并计算三相电压相位。直流侧电压跟踪部分通过PI控制环节计算稳压电流，稳定直流侧电压。

无功补偿电流计算环节无功电流检测采用ip-iq法，三相电流通过Tabc-pq变换得到ilp，ilq，再经低通滤波器得到直流分量，即为三相电流正序有功、无功电流分量幅值。Tabc-pq变换如下式：

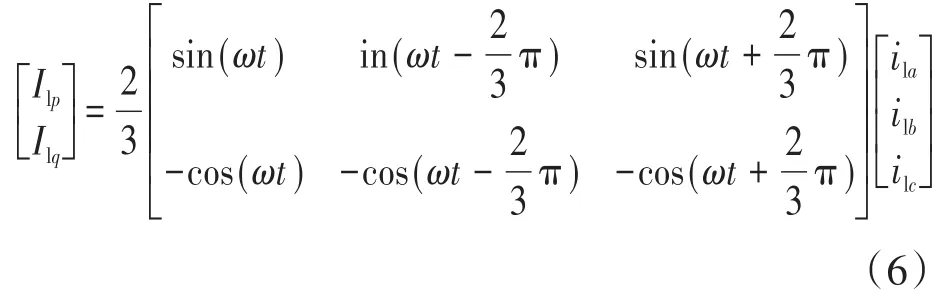
式中：ila，ilb，ilc分别为三相瞬时负荷电流；Ilp，Ilq分别为p-q坐标系有功、无功分量。

ip-iq法仅选用sin（ωt），-cos（ωt）进行计算，在计算过程中不会出现畸变的谐波成分，能够对负荷中正序无功、负序电流进行准确检测。

依据设定的功率因数或补偿要素权重，就可计算无功补偿电流。

负序电流检测计算环节中负序电流检测也采用ip-iq法检测，经Tabc-dq变换、滑动均值滤波得到负序电流有功分量、无功分量，计算负序电流幅值、相位。最后通过解析几何法计算得到最优负序补偿解。其中，综合优化补偿算法模块流程图如图8所示。

图8 解析几何法求解最优解流程图Fig.8 Flow chart of solving optimal solution by analytic geometry method

无功补偿电流、负序补偿电流及稳压电流叠加就可得到参考电流。内环电流跟踪控制可采用准PR控制，其传递函数如下式所示：

式中：ωc为截止频率；ω0为基波频率；Kp，Kr为准PR控制系数。

准PR控制动态性能良好，能实现交流正弦信号无静差跟踪，准PR控制在诸多文献已有详细讲解[18-19]，在此不再赘述。

3 仿真结果对比

3.1 系统参数设置

为了验证所提TPBC优化综合补偿控制策略有效性，基于PSCAD/EMTDC进行次暂态仿真，分析比较在系统拓扑及参数相同时，优先确定无功补偿电流，TPBC不足以对负序完全补偿的工况下，两种补偿策略的负序补偿效果。仿真系统参数如下：电网电压us=380 V，最大允许相电流幅值Ilim=100 A，结构为三相桥，网测连接电感Lm1=0.6 mH，设备侧连接电感Lm2=1 mH，模块直流电压Udc=800 V，模块直流电容Cd=3 000 μF，模块开关频率fs=10 kHz。

3.2 补偿效果对比

仿真过程中，0.65 s前负荷运行在工况1，0.6 s时刻TPBC开始使能，对无功、负序进行补偿，0.65 s负荷切换至工况2，0.7 s负荷切换至工况3。

TPBC常规综合补偿策略与优化综合补偿策略补偿效果对比如图9所示。图9a为TPBC常规补偿综合策略补偿电流波形图，图9b为TPBC优化综合补偿策略补偿电流波形图，如两图所示，两种补偿策略补偿电流幅值都未超过最大允许电流Ilim。图9c为常规综合补偿策略下PCC电流波形，图9d为优化综合补偿策略下PCC电流波形。图9e为无功电流幅值曲线对比图，图9f为负序电流幅值曲线对比图，图9g为负序电流相位曲线对比图，其中实线表示负荷电流参数，紧虚线表示常规补偿策略下PCC处电流参数，点划线表示优化补偿策略下PCC处电流参数。由图9e、图9f可以看出，在相同工况下，无功电流补偿相同时，优化综合补偿策略负序补偿效果更优，由图9g可看出优化综合补偿策略下PCC处负序电流相位相较于负荷负序电流，相位发生了变化。

常规综合补偿策略和优化综合补偿策略下，三种工况稳态时，补偿前后负序电流相位和幅值具体数值如表3所示。

表3 负序电流幅值相位对比表Tab.3 Negative sequence current amplitude and phase comparison table

如图9g及表3所示，常规综合补偿策略下PCC处负序电流相位与负荷负序电流相位相等，优化综合补偿策略下PCC处负序电流相位与负荷负序电流相位相比，发生了变化，这也是优化综合补偿策略的特点。

如图9f及表3所示，与常规综合补偿策略相比，优化综合补偿策略下PCC处负序电流更小。由表4可知，优化综合补偿策略相较于常规综合补偿，工况1时，负序剩余度下降率6.3%，工况2时，负序剩余度下降2.9%，工况3时，负序剩余度下降4.6%。验证了所提优化综合补偿策略有效性，验证了在不增加TPBC任何功率容量的基础上，优化综合补偿策略提高了TPBC设备利用率和补偿效果。

图9 常规与优化补偿控制策略仿真对比结果Fig.9 Simulation comparision results of conventional and optimal compensation control strategies

4 结论

本文针对有限容量TPBC无功电流负序电流综合补偿，提出优化综合补偿理论，基于解析几何与平面规划思想求解最优补偿解。分析优化补偿策略的原理、仿真验证优化综合补偿策略的有效性，并有以下结论：

1）针对有限容量TPBC无功负序电流综合补偿，优先确定无功补偿电流，在不增加TPBC任何功率容量的基础上，优化综合补偿策略相对于常规综合补偿策略，提高了负序电流补偿效果，提高了TPBC设备利用率。

2）综合补偿策略动态响应速度主要取决于电气量检测的计算延时，在主流数字信号处理计算速度下，并不会由于增加了一部分优化计算而降低动态特性。

3）对于正序有功、正序无功、负序电流耦合的新能源并网变流器，优化综合补偿算法也适用，这也是下阶段研究方向。