BDS-2/BDS-3联合精密单点定位性能分析

崔 健, 米宏志, 朱明水, 马东岭, 柴大帅

(山东建筑大学 测绘地理信息学院,山东 济南 250101)

北斗导航卫星系统(BeiDou Navigation Satellite System,BDS)是我国自主建设、独立运行并可以向全球用户提供全天候、全天时、高精度导航、定位、授时的全球导航卫星系统(global navigation satellite system,GNSS)[1-2]。北斗三号全球卫星导航系统(BDS-3)于2020年7月31日全面建成并正式开通,具备基本定位导航授时、区域星基增强、区域精密单点定位(precise point positioning,PPP)、短报文通信和国际搜救等多种服务能力[3-4]。BDS-3采用3种轨道卫星组成的混合星座设计,整个系统空间段由24颗中地球轨道(medium earth orbit,MEO)卫星、3颗倾斜地球同步轨道(inclined geosynchronous orbit,IGSO)卫星、3颗地球静止轨道(geostationary earth orbit,GEO)卫星组成[5]。BDS-3在北斗二号全球卫星导航系统(BDS-2)的B1I、B3I信号基础上,还增加了2个兼容互操作性更强的信号B1C、B2a,其中B1C(1 575.420 MHz)信号与美国的全球定位系统(Global Positioning System,GPS)的L1信号以及欧洲的Galileo导航卫星系统的E1信号兼容互操作,B2a(1 176.450 MHz)信号与GPS的L5C信号以及Galileo的E5a信号兼容互操作[6]。

卫星导航定位的精度和可靠性在很大程度上取决于卫星观测数据的质量,对于近期组网完成并已投入使用的BDS-3,数据质量的评估尤为重要。文献[7]对BDS-2观测数据质量进行分析,研究信噪比(signal-to-noise ratio,SNR)、多路径(multi-path,MP)效应随高度角的变化情况,实验结果表明,BDS-2的观测数据质量略优于GPS观测数据;文献[8]研究表明,BDS-3卫星的数据质量与BDS-2相当,甚至更高,且伪距中不存在明显的卫星端MP偏差;文献[9]研究发现,BDS-3试验卫星的观测数据质量已达到与GPS L1/L2/L5和Galileo E1/E5a/E5b相当的水平;文献[10]对BDS-3和BDS-2的观测数据质量进行分析,结果表明除伪距MP误差外,BDS-3系统观测数据的总体质量与GPS相当,甚至优于GPS。以上研究大多是对BDS-3观测数据的质量分析,但由于在相应研究截止时间BDS-3还未全面建成,BDS-3与BDS-2的比较分析还不够全面。

在BDS-2和BDS-3的PPP方面也有一些研究成果。文献[11]发现,BDS-2/BDS-3联合(BDS-2/3)PPP静态解在E、N、U方向的定位精度在mm级到cm级,收敛时间为20～30 min;文献[12]研究表明,BDS-2的静态PPP可以达到cm级;文献[13]中的非组合PPP模型可实现水平方向mm级至cm级,高程1～3 cm级静态定位精度;文献[14]中,在非差非组合模型下,BDS-3静态PPP精度水平方向优于2.0 cm,高程方向优于2.5 cm,收敛时间在31 min左右。但是,在BDS-3全面建成后,对于BDS-2/3静态PPP性能分析的相关研究较少。

本文在BDS-3全面建成、BDS全球组网完成的背景下,选择亚欧大陆和非洲大陆部分多卫星系统试验网(Multi-GNSS Experiment,MGEX)跟踪站的观测数据,对BDS-2与BDS-3卫星的数据质量进行分析,并将BDS-3的兼容互操作频点B1C和B2a与GPS的L1和L5C频点数据质量进行对比,最后对BDS-2与BDS-2/3的PPP精度和收敛性进行比较分析。

1 非差非组合PPP函数模型

观测数据的好坏直接影响导航定位的性能,非差非组合PPP能够有效避免观测噪声和MP误差放大的问题,同时获取电离层延迟参数信息,为各类用户提供高精度的位置、时间和大气延迟(对流层和电离层延迟)信息,具有非常重要的应用价值,也是近年来GNSS领域的又一个研究热点[15]。所有GNSS所有频率的观测值都可以用非差非组合函数模型建立观测方程[16],即

(1)

(2)

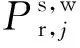
2 实验分析

2.1 数据概况

由于受测站环境和位置的影响,各测站接收BDS卫星信号的质量存在差异,同时为了全面分析BDS-2和BDS-3卫星信号的性能,本文在亚欧大陆和非洲大陆中选取7个MGEX测站,利用2020年年积日(day of year,DOY)第257天至第263天(9月13日至9月19日)共7 d的观测数据进行分析,每个测站的数据采样间隔为30 s。本文用于PPP解算的测站分布如图1所示。

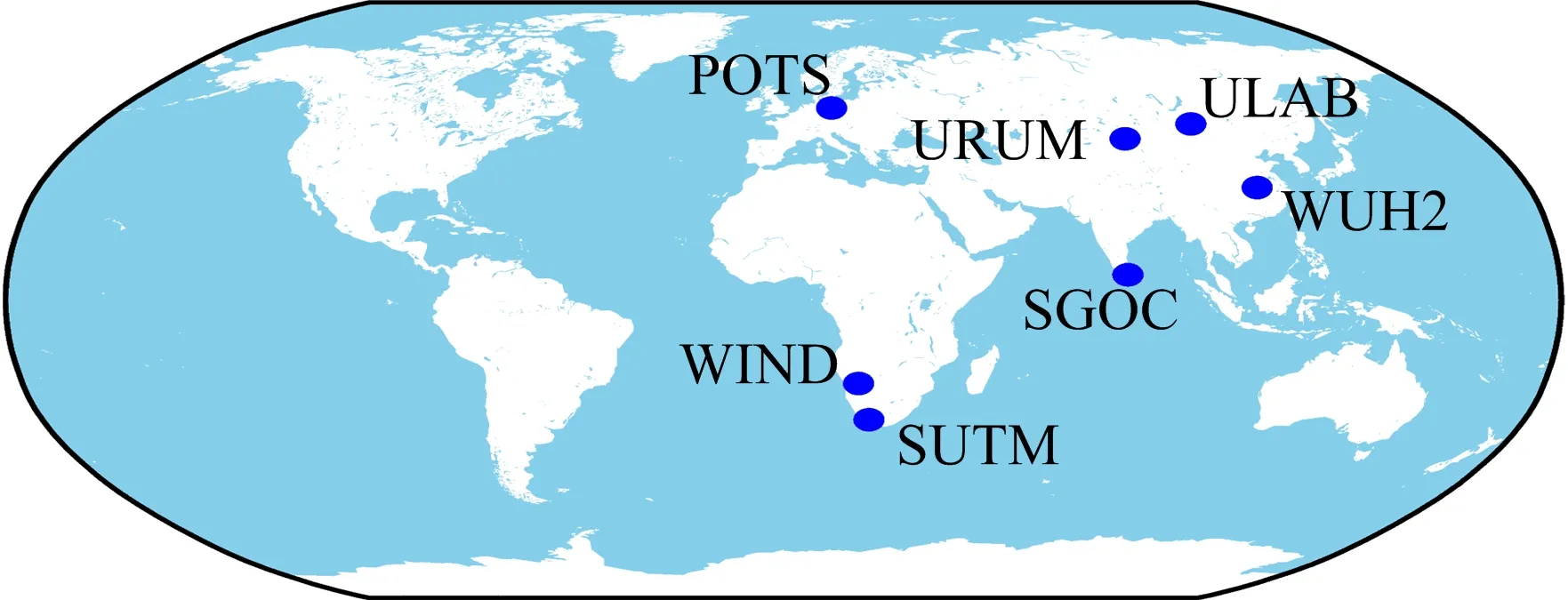
图1 本文用于PPP解算的测站分布示意图

7个测站的接收机型号均为“JAVAD TRE-3”,天线类型均为“JAVRINGANT-G5T-NONE”,其位置信息见表1所列。

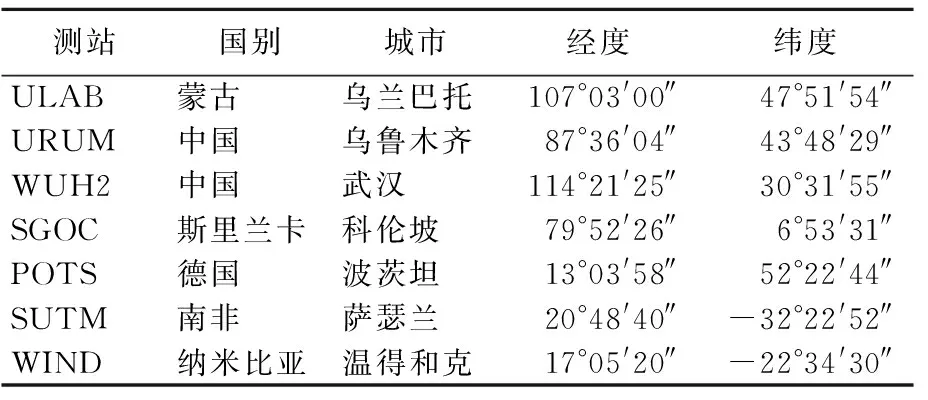
表1 测站位置信息

2.2 数据质量性能分析

2.2.1 SNR分析

SNR是指载波信号强度和噪声强度的比值,SNR数值越大,表明观测数据质量越好。

由于篇幅有限,本文在亚欧大陆和非洲大陆的7个测站中选取3个测站(URUM、SUTM、POTS)来分析BDS-2和BDS-3的SNR差别,并且选择MEO卫星来作比较分析,其中选取BDS-2卫星C11和BDS-3卫星C34。

3个测站2颗MEO卫星所有频点SNR随高度角变化情况如图2所示。另外选取POTS测站对BDS-3的C34卫星2个兼容互操作频点B1C、B2a与GPS的G27卫星L1、L5C频点的SNR进行对比,结果如图3所示。

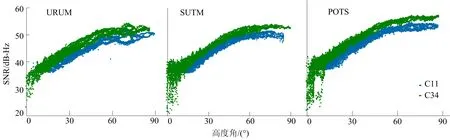
图2 3个测站2颗卫星SNR随高度角变化情况

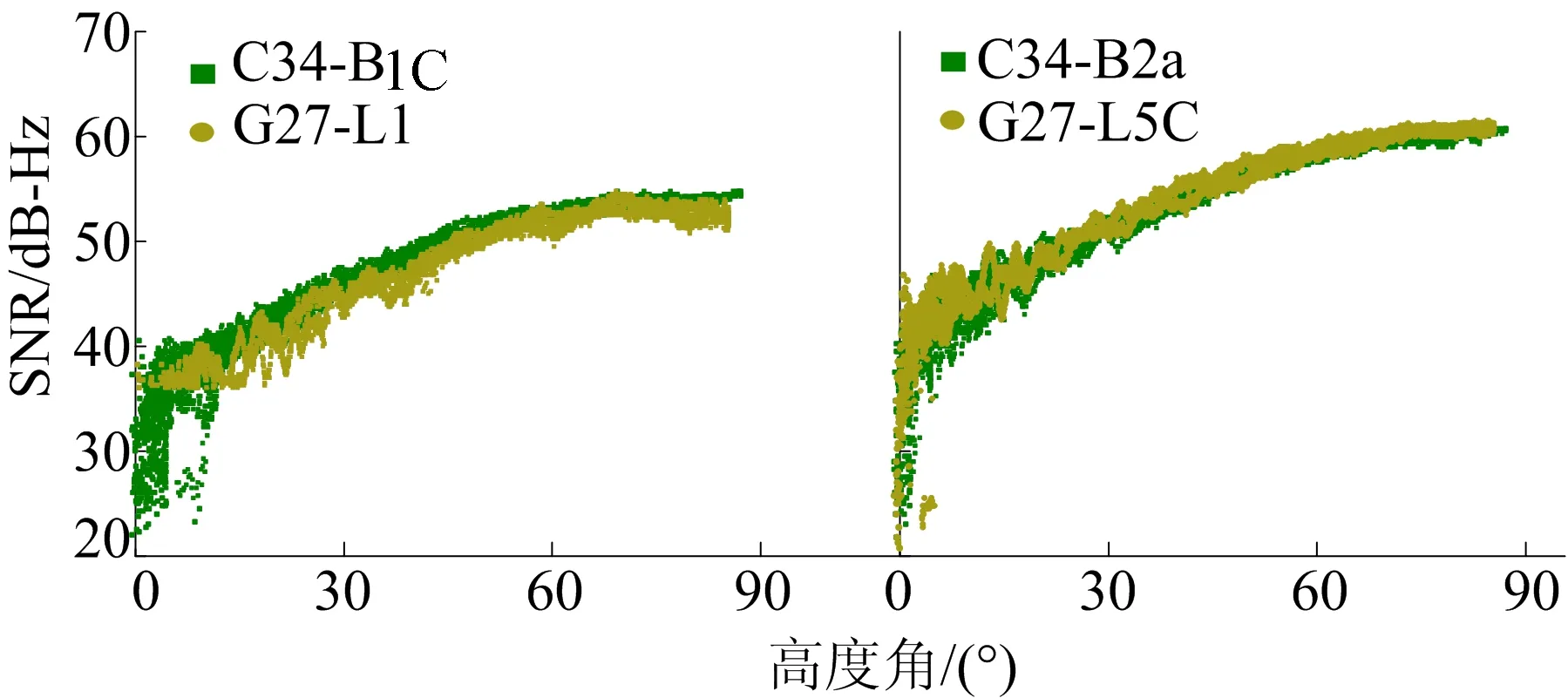
图3 POTS测站兼容互操作频点SNR随高度角变化情况对比

从图2可以看出:2颗卫星的SNR在3个测站都随高度角增加而增加,高度角为0°时的SNR都大于20 dB-Hz;在高度角趋于60°时,2颗卫星在3个测站的SNR均可达到50 dB-Hz以上;在3个测站中,与BDS-2卫星C11相比,BDS-3卫星C34的信号强度均有一定的提高。从图3可以看出:BDS-3的B1C频点信号强度较GPS提高4 dB-Hz左右;B2a频点信号强度与GPS基本一致,相差1 dB-Hz左右;在高度角达到60°后,BDS-3的B1C频点和GPS的L1频点的SNR均可达到55 dB-Hz以上,而BDS-3的B2a频点和GPS的L5C频点的SNR表现更为优异,可达到60 dB-Hz及以上。

2.2.2 卫星可见性与PDOP值分析

卫星定位精度不仅取决于观测值的精度,也取决于卫星的空间几何构型,而可见卫星数和位置精度因子(position dilution of precision, PDOP)值的连续和稳定性也是保证PPP位置收敛的重要条件。

7个测站BDS-2、BDS-3及BDS-2/3的卫星可见数和PDOP值随历元时刻的变化情况如图4、图5所示。

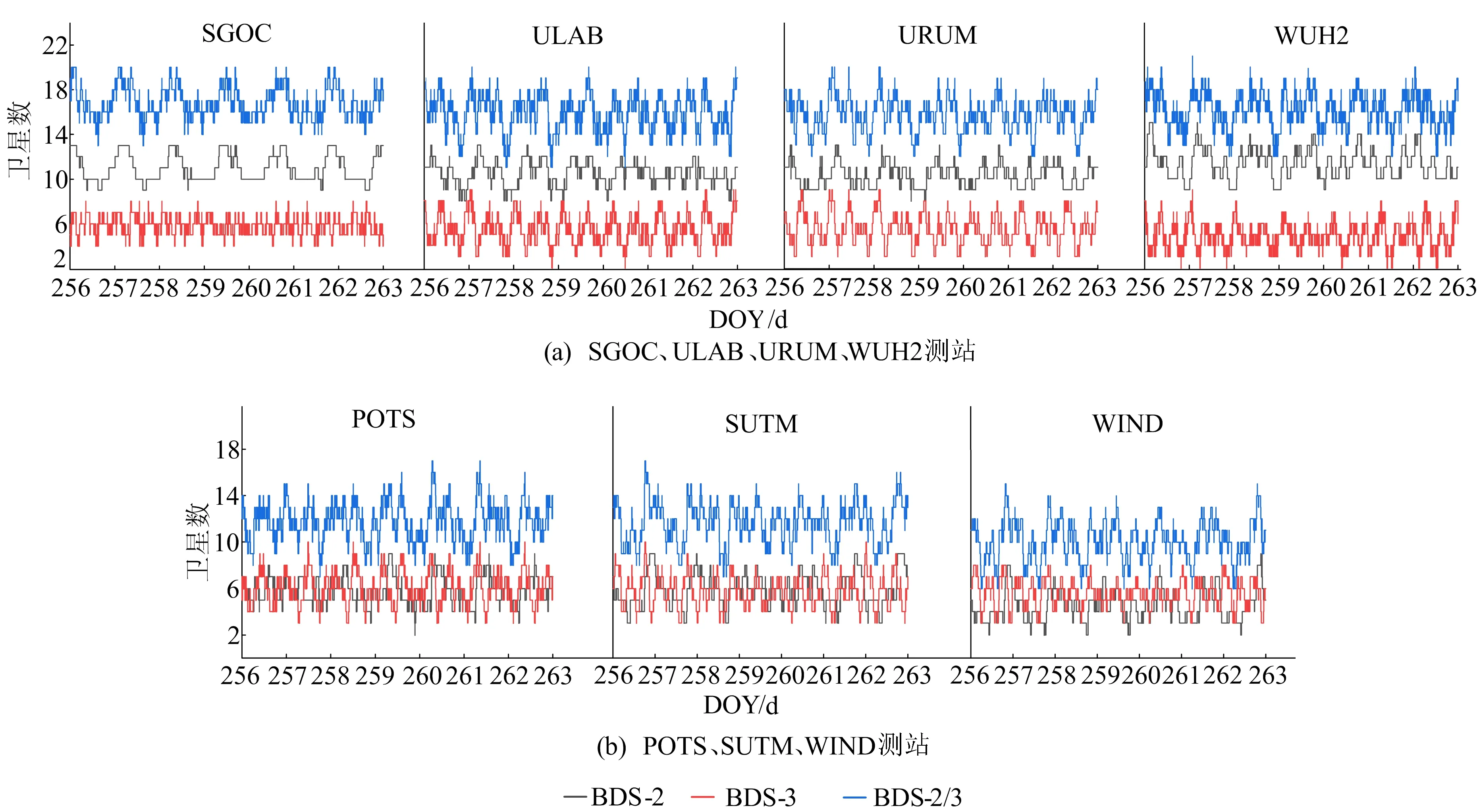
图4 7个测站BDS-2、BDS-3及BDS-2/3的卫星可见数

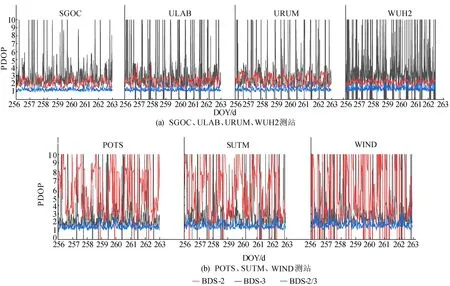
图5 7个测站BDS-2、BDS-3及BDS-2/3的PDOP值

从图4可以看出:在SOGC、ULAB、URUM、WUH2测站,同一历元下BDS-2的卫星可见数明显优于BDS-3,BDS-2的卫星可见数始终保持在8颗及以上,平均为10.7颗,BDS-3的卫星可见数在2～10颗范围内,平均为5.2颗,其中SGOC测站的卫星可见性最佳,其BDS-3卫星可见数均在4颗及以上,最高可达8颗,其BDS-2的卫星可见数在9～13颗内;而在POTS、SUTM、WIND测站,BDS-2与BDS-3的卫星可见数相差不大,很多历元下BDS-2卫星可见数不足4颗,平均为5.3颗,BDS-3卫星可见数平均为5.7颗,可见卫星数目相对较少。

从图5可以看出:在SGOC、ULAB、URUM、WUH2测站，BDS-2的PDOP值整体保持在4以下,而BDS-3的PDOP值偏差较大,这是由于在这4个测站中BDS-3卫星的可见数较少,卫星空间几何构型较差,BDS-2/3的PDOP值表现较优,整体保持在2以下且没有较大波动;在POTS、SUTM、WIND测站中BDS-2和BDS-3的PDOP值均表现较差,其原因是这3个测站BDS-2和BDS-3可见卫星数目较少,导致空间几何构型较差,PDOP值波动较大;而BDS-2/3的可见卫星数增加,卫星空间几何构型较好,PDOP值得到明显改善,基本保持在3以下。由此可见,BDS-2/3由于可见卫星数增多,卫星系统的几何构型得到改善,PDOP值变好。

2.2.3 MP效应分析

MP效应是指在接收机收到的卫星发射信号中,同时包含测站附近物体表面1次或多次反射的信号,所有信号叠加在一起而产生的时延效应。

由于篇幅有限,为了综合分析MP效应,本文根据3个测站(URUM、SUTM、POTS)的观测数据,选取BDS-2的MEO卫星C11对B1I、B3I频点进行MP误差分析,结果如图6所示。

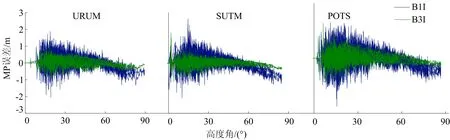
图6 C11卫星B1I、B3I频点MP误差随高度角变化情况

由于B2a信号只在BDS-3卫星上播发,本文分别在3个测站中选取BDS-3的MEO卫星C34对B1C、B2a频点进行MP误差分析,结果如图7所示。

为了综合评估BDS-2和BDS-3各频点的MP效应,对7个测站各频点所有卫星最终的MP误差均方根(root mean square,RMS)值进行统计,结果见表2所列。

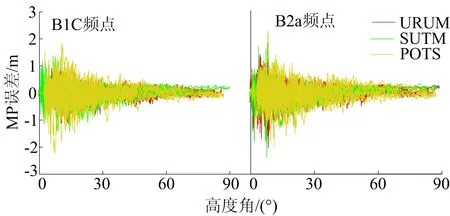
图7 C34卫星B1C、B2a频点MP误差随高度角变化情况

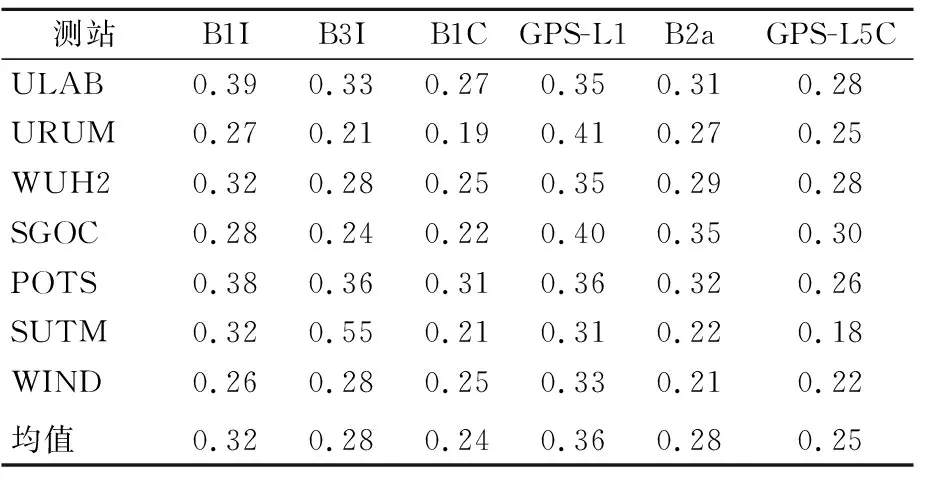
表2 各频点MP误差RMS统计结果 单位：m

由图6、图7可知:3个测站2个频点的MP误差均随着高度角增大而减小,并且主要波动在2 m以内;BDS-2的C11卫星MP误差出现明显的向负偏移现象,而BDS-3的C34卫星没有这种明显变化。

在不同的测站中,MP误差会受到观测条件和接收机型号的影响而有所差异,但是在同一测站中各频点间的MP误差相对大小关系一致。由表2可知,各测站各频点MP误差的RMS值与均值的差主要在0.07 m以内,SUTM站B3I频点的MP误差RMS值波动较大,其与URUM测站相差最大,为0.34 m,因此本文在计算B3I频点的MP误差RMS均值时不考虑SUTM测站。对表2中各频点的RMS均值进行分析可知,B1C和B2a频点与B1I和B3I频点相比,其MP效应表现较优。

从图7可以看出,在高度角较大时,对于B1C、B2a频点的MP误差并没有出现明显的向负偏移现象,而且由表2可知,B1C频点的MP表现优于GPS的L1频点,B2a频点的RMS值均值与L5C频点仅相差0.03 m。由此可见,BDS-3在兼容互操作频点上的MP误差表现较优。

2.3 定位精度与收敛性分析

为了研究BDS-3的加入与完善对BDS定位精度和收敛速度的影响,本文采用非差非组合模型进行PPP解算,主要比较分析BDS-2和BDS-2/3静态PPP精度,并统计E、N、U方向定位误差连续20个历元均小于10 cm所需要的时间。由于POTS、SUTM、WIND 3个测站的卫星可见性和PDOP值表现较差,在一些历元下BDS-2卫星不足4颗,因此本文仅选取另外4个测站(SGOC、ULAB、URUM、WUH2)进行分析。

4个测站2020年在DOY第258天BDS-2、BDS-2/3静态PPP偏差如图8所示。

4个测站连续7 d的定位误差RMS统计结果见表3所列,4个测站连续7 d静态PPP收敛时间如图9所示。

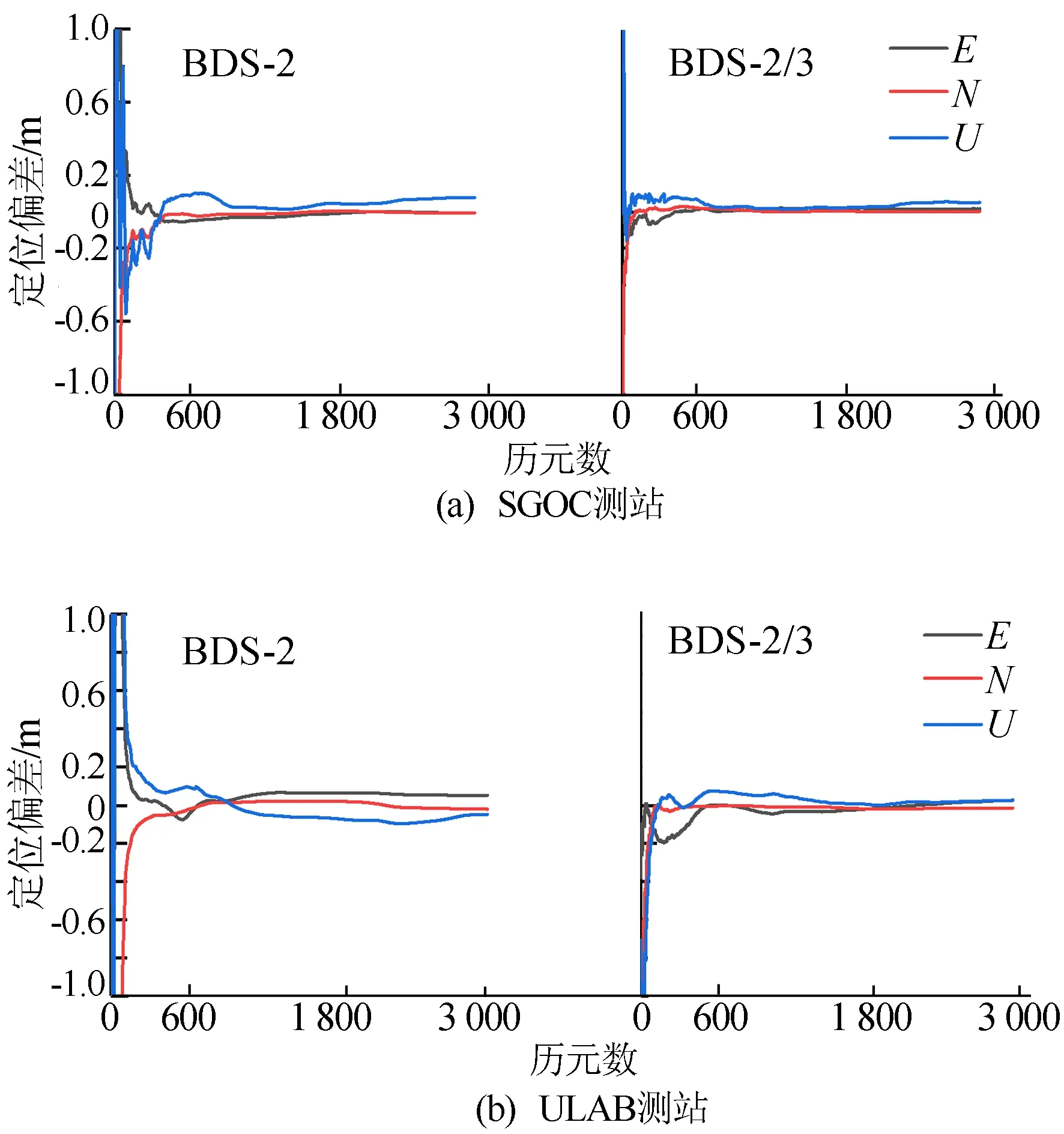
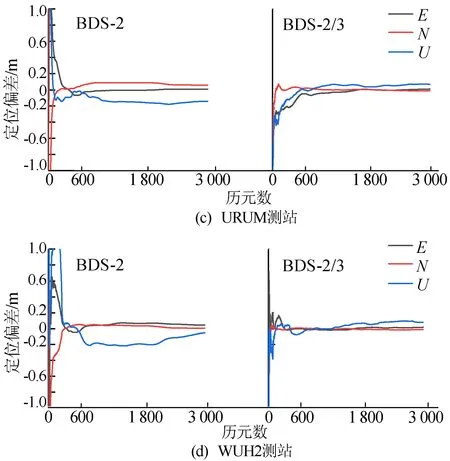
图8 4个测站定位偏差时间序列

测站BDS-2ENUBDS-2/3ENUSGOC2.71.55.82.21.24.4ULAB5.44.56.22.51.43.5URUM2.15.27.62.91.45.3WUH25.43.38.11.61.16.1均值3.93.67.02.31.34.8

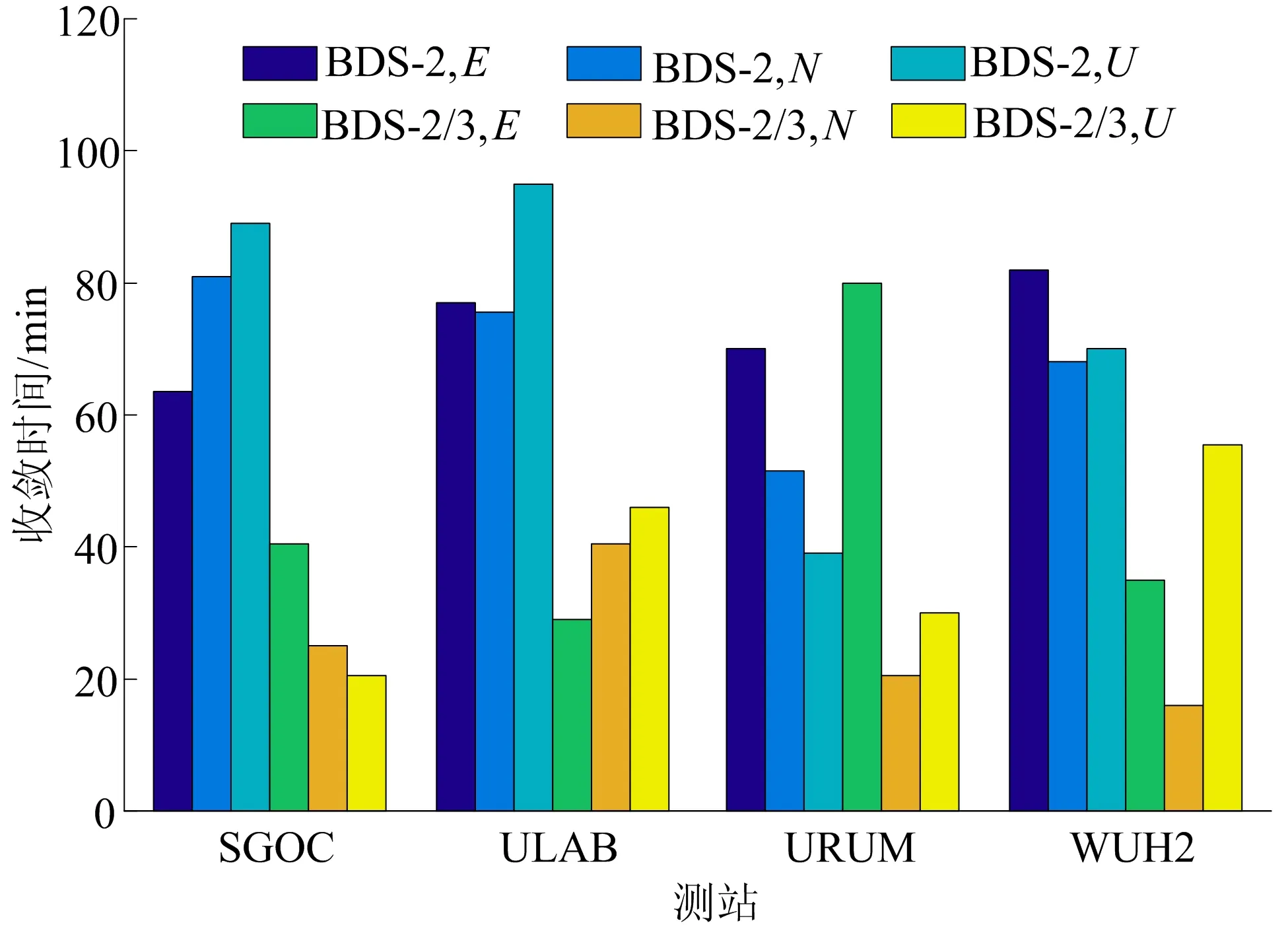
图9 4个测站连续7 d静态PPP平均收敛时间

从图8、表3可以看出,4个测站BDS-2与BDS-2/3均能实现10 cm以内的定位精度,相比于BDS-2,BDS-2/3定位精度得到有效改善。BDS-2的E方向平均定位精度为3.9 cm,N方向为3.6 cm;BDS-2在U方向的定位精度表现较差,在URUM和WUH2测站的某些历元时刻下最差可达20 cm,平均为7.0 cm;在加入BDS-3后,BDS-2/3的定位精度在E方向为2.3 cm(提升41%),N方向为1.3 cm(提升64%),U方向为4.8 cm(提升31%)。

由图9可知,BDS-2的收敛时间相对较长,在E、N、U方向上平均为73.1、69.0、73.3 min,这是由于其在所选测站中的卫星可见性和PDOP值表现较差,其轨道精度较差,使其PPP精度相对较差,收敛时间相对较长。加入BDS-3后,BDS-2/3的可见卫星数比BDS-2有所增加,可以大幅缩短收敛时间,BDS-2/3在E、N、U方向上收敛时间平均为28.2、25.5、38.0 min,大约在40 min内就可以达到10 cm的定位精度,这是由于BDS-3的加入为BDS带来更多的可观测卫星,而且BDS-3卫星中大多为MEO卫星,为BDS提供了良好的几何构型。

3 结 论

本文根据MGEX观测站数据,综合评估BDS-2和BDS-3的数据质量,对比分析BDS-2和BDS-2/3的静态PPP精度和收敛速度,得到以下结论:

(1) 观测数据质量方面,在SNR上BDS-3的表现优于BDS-2,在MP误差方面,与BDS-2相比,BDS-3的表现较优,并且没有观测到明显的系统偏差,在兼容互操作频点上BDS-3的SNR和MP表现也较优于GPS;但在卫星可见性和PDOP值方面,实验数据显示BDS-3的表现差于BDS-2,在一些历元下BDS-3的卫星可见数不足4颗,其卫星空间几何构型较差,PDOP值在各测站中均有较大波动,而BDS-2/3卫星可见数和PDOP值都得到明显改善。

(2) 静态PPP性能方面,BDS-2在E、N、U方向定位精度平均为3.9、3.6、7.0 cm,BDS-2/3在E、N、U方向平均为2.3、1.3、4.8 cm,相比于BDS-2分别提高41%、64%、31%;收敛时间方面,BDS-2在E、N、U方向上平均收敛时间分别为73.1、69.0、73.3 min,BDS-2/3的收敛时间相比于BDS-2从80 min左右缩短至40 min左右,大约提高50%,在E、N、U方向上平均为28.2、25.5、38.0 min。相比于BDS-2,加入BDS-3卫星后能显著提升BDS静态PPP精度和收敛速度。

随着未来BDS精密产品精度的提高,BDS的PPP精度和收敛时间都将得到进一步提升。