金刚石压腔结合高速录像进行气-液体系中气相溶解、出溶动力学原位研究

赵 韬， 王世霞

（上海理工大学 材料与化学学院，上海 200093）

火山喷发是岩浆水蒸气溶解出溶过程，其动力源自水蒸气从岩浆中出溶，溶蚀速率决定了火山喷发的力量和强度。气泡在液相体系中溶解出溶过程是相对简单的多相反应，气液相溶解和出溶动力学的研究对于爆发式火山喷发动力学追踪具有重要意义。气液两相体系中气相溶解和出溶的研究主要为水蒸气气泡从硅酸盐熔体中的出溶和生长[1-2]，Liu 等[1]建立了硅酸盐熔体中气泡的生长模型，结果表明，气泡的生长速率随温度、初始总H2O 量的增加而增加，随气泡尺寸的增加而略有增加。Martel 等[2]利用光学显微镜和视频记录对硅熔体中的原位高压和高温气泡的生长进行了研究，并监测了气泡成核、气泡生长和玻璃化转变。当前研究较多集中于常温常压条件下气液体系中气相动力学反应、啤酒和香槟中气泡生长的化学动力学和物理动力学[3-5]、海水内上升的CO2液滴的对流溶解[6-10]、火山活动产生的CO2在熔岩湖中的溶解程度等[11-17]。

温度和压力是影响气液两相中气相溶解和出溶的重要因素，但高温高压下气相溶解、出溶动力学研究较少，因此本文应用水热金刚石压腔，结合气液两相压力-温度轨迹的均一温度，追踪体系中气相溶解、出溶过程，得到气相出溶过程中气泡体积生长参数和气泡溶解过程中气泡体积变化与反应时间之间的良好的线性关系。

1 实验方法

水热金刚石压腔实验装置[18-21]如图1 所示。压腔主体部分由一对金刚石压砧和铼垫片组成，相对其他金属片，铼片具有弹性好、惰性强、高温时不易和样品体系发生反应等特点。体系使用电阻丝外加热法，体系温度由温控器测得并校正。

金刚石压腔中气体样品装样难度较大。但是对于空气-H2O 体系，在金刚石压腔中装入压标物质石英、蒸馏水，在密封过程中封入一定量的空气（主要成分为78%的N2和21%的O2），即形成简单的多相体系，如图2 所示。对装有气泡的液相实验体系进行升温降温调节，在重复升降温过程中，气泡消失的温度逐渐降低并趋于相同。重复升温降温直至气泡消失的温度差在±1 ℃，记录此时的温度，即为该体系的均一温度Tm[22]。

高速录像技术是记录体系快速反应过程的唯一手段，本研究利用配置了摄像头的光学显微镜的高速录像技术对快速反应过程进行记录，如图3所示。高速录像设备分辨率为33 帧/s，之后利用GIF video gear 软件对录像文件进行分解，利用Image-Pro Plus 软件对分解照片进行处理，如图4 所示。应用Image-Pro Plus程序测得气泡面积S，进而推算出气泡半径R。同时也可以应用Image-Pro Plus程序测得气泡直径D，推算出气泡半径R′。表中显示R和R′之间的差值△R基本稳定在0.45 μm 左右，除最初气泡初生成时半径误差在8%，其余结果显示半径误差均小于5%。本研究选择应用测量气泡面积计算所得的气泡半径R，可进一步减小实验误差。

图4 Image-Pro Plus 程序分析气泡面积Fig.4 Analysis of bubble area using Image-Pro Plus program

实验高速录像的分辨率为33 帧/s，设置温度发生变化时即温度升高和降低的初始时刻t0，此时的照片号为N0，则对录像进行分解得到的照片N所经历的反应时间为

研究根据高速录像得到的照片确定气泡出现和消失的时间，实验将达到均一温度的气-液相体系进行快速降温，并将降温过程中气泡出现的时间作为反应初始时间t=0 s。利用Image-Pro Plus 软件对照片中气泡面积和直径进行测量（如图4 所示），通过计算得到气泡体积生长参数F=（V-V0）/（Ve-V0）。式中：V0为初始气泡体积；Ve为气泡生长达到平衡时的体积。

2 实验结果及讨论

达到均一温度的气-液相体系在降温过程中会重新生成气泡，气泡从液相中的出溶过程分为成核过程和生长过程。相同密度条件下的体系，降温速率不同，气泡出现的时间不同。表1 实验结果显示，均一温度状态下降温速率越大，气泡出现所需的时间越短，因此气泡出溶实验中要控制降温速率和降温幅度。

表1 不同冷却速率下气泡出现的时间Tab.1 Appearance time of bubble with different cooling rates

2.1 气-液体系中气相的出溶

图5 为均一温度275.6 ℃气-液体系下降温至气泡出溶的实验过程。初始均一温度275.6 ℃以1.6 ℃/s 的降温速率降至过冷温度259.1 ℃，之后温度缓慢升高至259.7 ℃，随后18.85 s 时气泡出现并逐渐变大，气泡出溶增大过程释放热量使体系温度继续升高，至260.3 ℃并保持恒温，变化幅度±0.2 ℃。

图5 气相出溶过程中气泡随时间的变化Fig.5 Changes of bubble with time during exsolution of gas phase

气泡生长中各参数如表2 所示。根据气泡出溶达到平衡之后的数据，计算平衡时体积Ve为10 315 μm3，将气泡出现的时间作为初始时间t=0 s，此时气泡的体积V0为1 251 μm3（见表2），可计算出气泡生长参数F=（V-V0）/（Ve-V0）。应用Johnson-Mehl-Avrami-Kolmogorov（JMAK）模型按照一级反应速率方程进行拟合[23-25]，利用ln[-ln(1-F)] 对lnt作图，可得到气泡体积生长参数F与生长时间之间的关系，并进行线性拟合，结果如图6 所示。

图6 气相出溶过程中ln[-ln(1-F)]与lnt 的关系Fig. 6 Relation of ln[-ln(1-F)] and lnt during exsolution of gas phase

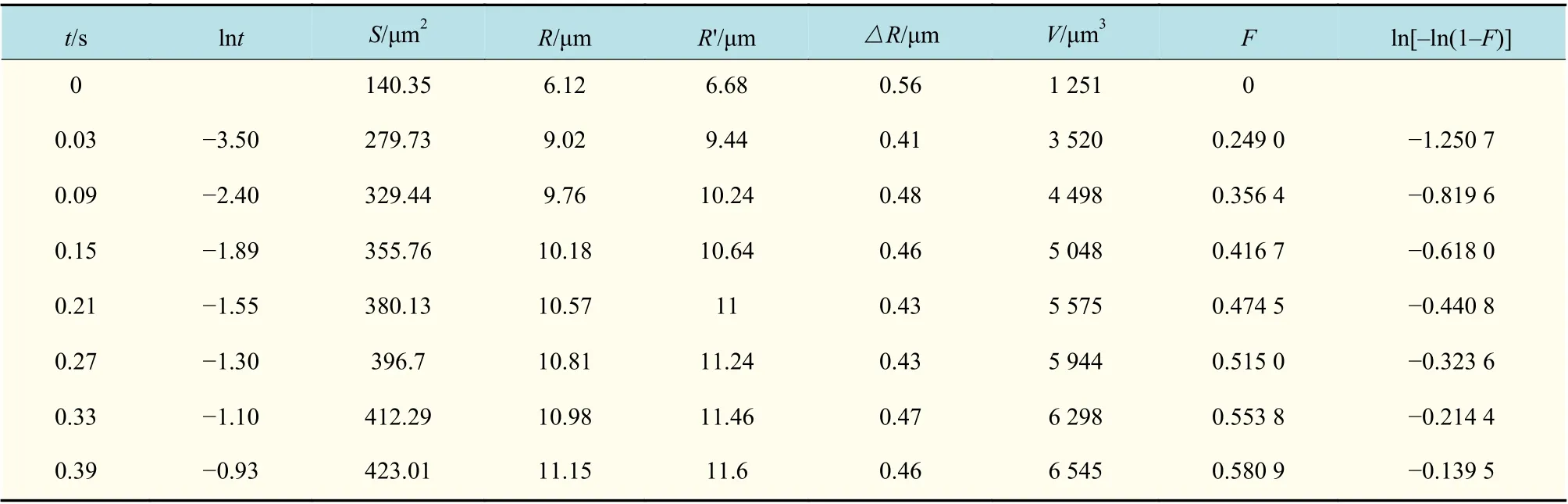
表2 气泡生长过程中各参数Tab.2 Data during the process of bubble growth

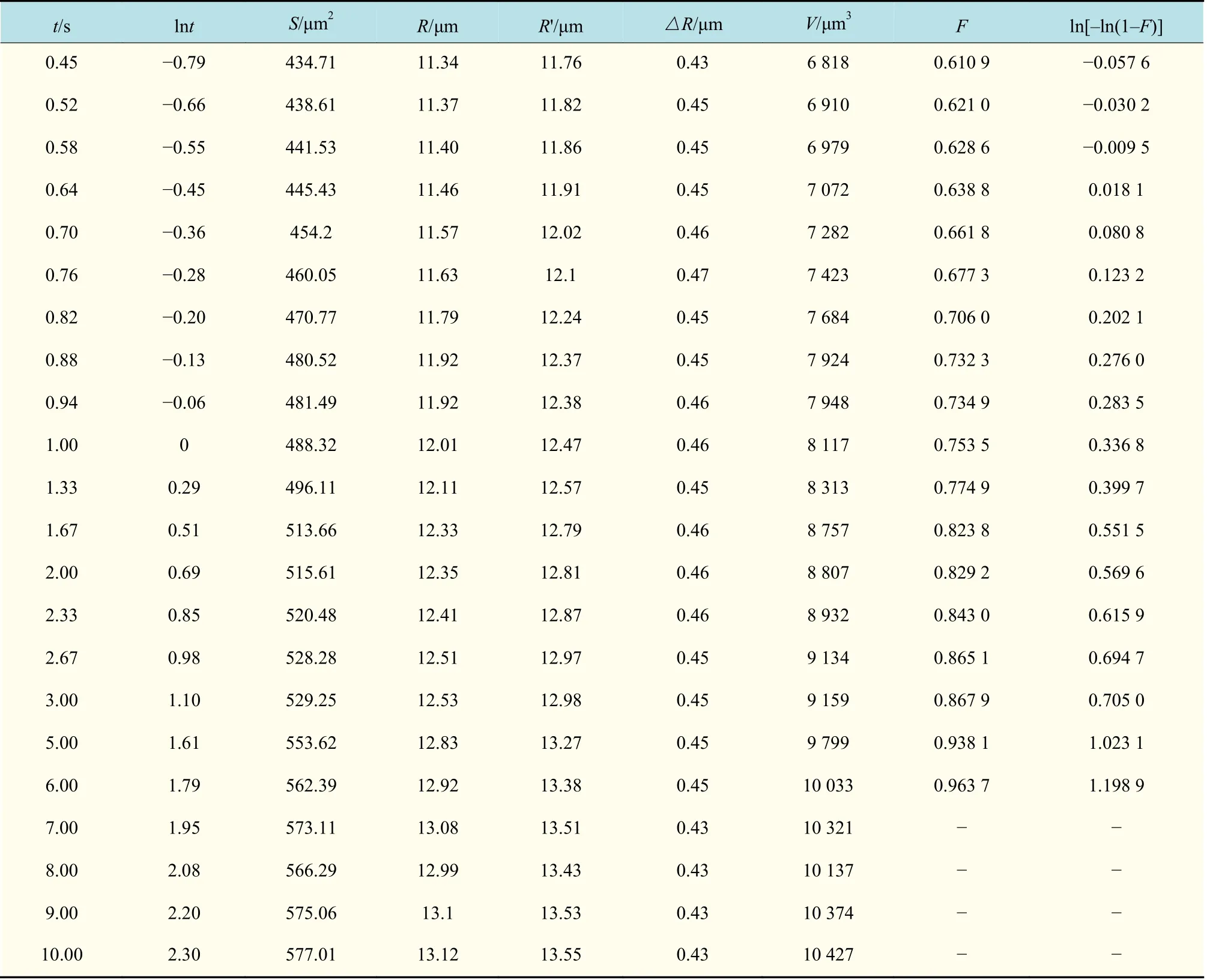
续表 2

拟合结果显示，反应级数n为0.455，与Zhang等[26]（n=0.551）在几个相同尺寸过氧化氢气泡生长过程中的拟合结果相近，进一步证明了气泡的生长很大程度上受扩散控制。

2.2 气-液体系中气相的溶解

对上述出溶并在260.3 ℃达到气-液相平衡体系的气泡进行气泡溶解过程实验。实验伊始以1～2 ℃/s 升温速率使体系温度升高，反应至16 s时，体系温度升至277.1 ℃，此升温过程中气泡发生一定程度的溶解。随后以0.05 ℃/s 速率降温，反应至30 s 时，体系温度波动降至276.2 ℃，之后保持体系恒温状态，变化幅度±0.2 ℃，直至气泡在66 s 时消失。

气泡溶解过程中半径随时间的变化趋势如图7和表3 所示。可见，气泡半径随时间的变化规律在16 s 前后有明显不同。16 s 之前，气泡半径随时间迅速减小，由初始的14.16 μm 降至6.02 μm；16～31 s 之间，气泡半径变化较小，由6.02 μm 降至5.54 μm；31 s 之后，气泡半径随着时间继续降低，但是变化速率明显低于16 s 之前的速率，直至66 s 时气泡完全溶解。结合表3 升温过程可知：在16 s 之前，温度由260.9 ℃升高至277.1 ℃，温度的升高伴随压力的升高，使液相体系空气溶解度增加（体系中空气的不饱和度增加），气泡溶解趋势增大，气泡半径随时间快速降低，溶解速率为0.509 μm/s；16～31 s 过程中，体系温度降至276.2 ℃，温度降低了0.9 ℃，气泡的溶解伴随由于温度压力降低所造成的膨胀作用，半径随时间变化不大；31 s 之后，体系温度（压力）保持恒定，体系中空气溶解度不再发生变化，气泡继续溶解，但是溶解速率明显低于16 s 之前的，为0.157 μm/s。

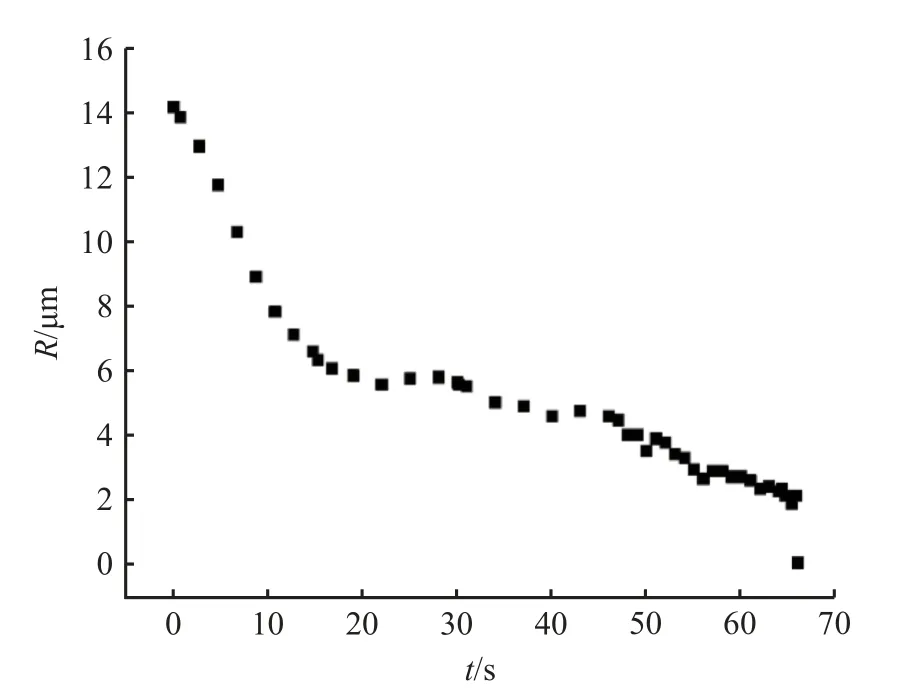
图7 气泡溶解过程中半径随时间的变化Fig. 7 Change of radius with time during bubble dissolution

表3 气泡溶解过程中的半径变化Tab.3 Changes of radius during bubble dissolution

实验过程中气泡经历了0～16 s 和16～31 s 两个溶解过程，结合F=（V-V0）/（Ve-V0），利用JMAK方程对体积随时间的变化数据进行ln[-ln(1-F)]对lnt作图，分别得到两个溶解阶段F与t之间的关系，并进行线性拟合，结果如图8 所示。

图8 气相溶解过程中ln[-ln(1-F)]与lnt 的关系Fig.8 Relation of ln[-ln(1-F)] and lnt during dissolution of gas phase

拟合方程得到16 s 之前的反应速率常数k1为0.215 s-1，31 s 之后的反应速率常数k2为0.059 9 s-1，前者为后者的3.6 倍。根据半径计算得到16 s 前和31 s 后的溶解速率分别为0.509 μm/s 和0.157 μm/s，前者为后者的3.24 倍。两种计算结果基本一致，这表明随着体系温度变化的不同，溶解阶段不同，溶解反应速率不同。

2.3 多气泡体系溶解

对于单气泡体系，不同温度变化阶段，气泡溶解反应速率不同。对于多气泡体系来说，除温度变化影响气泡溶解反应速率外，气泡半径不同，对其反应速率的影响也不同。本文就气泡半径对气泡溶解速率的影响进行了进一步研究。图9为含有不同初始半径的3 个气泡的水溶液体系。气泡1，2，3 的初始半径分别为7.70，6.95，6.30 μm。实验伊始，体系缓慢升温至226 ℃，3 个不同半径的气泡均发生了一定程度的溶解；随后，体系缓慢降至224 ℃，并保持恒温状态，直至气泡完全溶解。

图9 3 个气泡的多气泡体系Fig. 9 Multi-bubble system with three bubbles

图10 为初始半径不同的3 个气泡的半径随反应时间的变化趋势。可以看出，0～10 s 反应过程中，随着体系温度的缓慢升高，3 个气泡的半径均随时间变化线性减小，对前10 s 的半径大小随时间变化的数据进行拟合，得到结果如下：

图10 3 个气泡在不同溶解阶段的半径变化Fig. 10 Radius change of three bubbles in different dissolution stages

结果显示，在0～10 s 升温过程中，气泡快速溶解，半径大小对气泡溶解速率影响较小，不同半径气泡的半径随时间的减小速率为0.15～0.18 μm/s，变化速率相近。经过0～10 s 的快速溶解后，气泡1，2，3 的半径分别为6.60，5.60，4.50 μm。在随后的10～36 s 过程中，体系经过缓慢降温直至恒温224 ℃，半径随反应时间呈现非线性关系，伴随着体系温度压力降低造成的膨胀作用，气泡半径随时间变化不大。在之后的36 s 至气泡消失过程中，通过利用JMAK 模型对体积随时间的变化进行拟合，结果如表4 所示。可见，随着气泡半径的减小，气泡溶解速率常数k逐渐变大，即气泡半径越小，溶解速率越大。

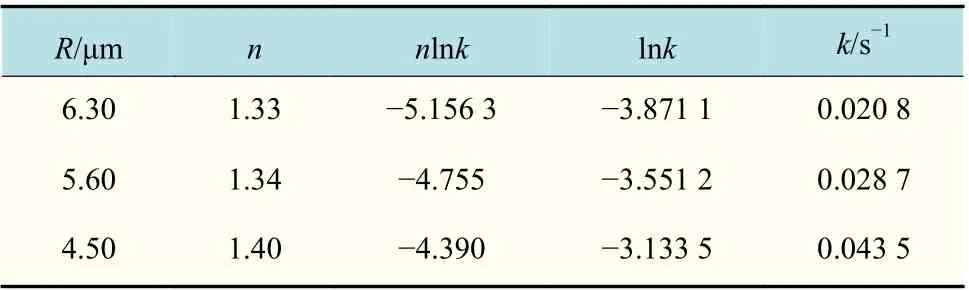
表4 在最终溶解阶段不同半径气泡的溶解速率Tab.4 Dissolution rates of bubbles with different radius in final dissolution stage

综上结果表明，对多气泡溶解体系，在初始升温快速溶解阶段，气泡溶解速率基本一致，半径对溶解速率的影响较小。后期恒温气泡缓慢溶解消失阶段，气泡半径对溶解速率的影响较大。

3 结 论

将金刚石压砧和高速摄像技术相结合，进行气液体系中的气相溶解和出溶动力学过程的原位研究，建立了气相溶解和出溶动力学模型。气泡从液相中的出溶过程分为成核过程和生长过程。空气-H2O 体系溶解和出溶动力学实验结果表明：在不同冷却速率下，气泡出溶所需的时间不同，冷却速率越大，气泡出溶所需时间越短。气液体系中，气泡溶解经历快速溶解、稳定溶解和缓慢溶解消失3 个阶段，快速溶解和缓慢溶解消失过程可用气泡出溶动力学模型标定。此外，对多气泡体系进行升温溶解实验，结果表明：快速溶解阶段，半径对溶解速率影响较小，不同半径气泡的溶解速率相近；缓慢溶解消失阶段，气泡的半径和溶解速率之间存在相关性，半径越小，溶解速率越大。