地铁隧道基底围岩动三轴试验研究

赵 楠

(中铁十九局集团轨道交通工程有限公司，北京 101300)

0 引言

随着国家经济建设的迅猛发展，交通基础设施建设正在如火如荼地展开。沈阳作为东北地区最大的城市，继纵贯沈阳东西与南北的地铁一号线、二号线贯通后，地铁三号线、四号线正在加紧施工。为保障地铁安全运营，有必要对地铁隧道围岩受列车荷载的影响进行研究。

近年来，国内外学者对动荷载作用下岩石的破坏机制研究成果颇丰。肖豪等通过GDS多功能动三轴试验系统对不同围压下的红砂岩风化土进行了研究，分析了试样在动荷载作用下强度特性[1]。杜瑞峰等通过自编程序对动三轴条件下泥质砂岩的变形模量进行了分析，并对试样的残余应变及能量耗散规律进行了总结[2]。谈亦凡等基于GDS动三轴试验系统对中风化和全风化砂岩进行了研究，并建立了风化岩石的累计塑性变形的预测模型[3]。何忠明等对不同含水率的路堤粗粒土进行了动三轴试验，并结合试验结果对邓肯-张模型进行了修正[4]。陈志敏等针对盐渍土路基冻胀、翻浆等病害问题，对不同水泥、石灰及粉煤灰掺量的路基土进行了动三轴试验研究[5]。冉武平等针对西部地区盐渍路基土病害问题，对不同应力路径、含盐量及含水率下的粗粒硫酸盐渍土进行了试验研究，分析了强度、回弹模量的变形规律[6]。聂如松等基于动三轴试验系统对铁路路基填料进行了研究，分析了路基填料的孔隙水压和累计塑性变形的演化规律[7]。刘超等为研究洱海地区的泥炭质土的力学性质，采用GDS系统对土样进行了动三轴试验研究，分析了加载频率、围压等影响因素对该地区土的影响规律[8]。唐毯等通过TAW-2000岩石三轴试验系统对不同围压及加载频率下砂岩的能量耗散机制进行了研究[9]。李丽华等为促进建筑垃圾的循环利用，通过室内大型三轴试验系统对建筑垃圾混合料的动力特性进行了试验研究，分析了阻尼比、动弹模量等的变化规律[10]。车高凤等通过动三轴试验WF-12440型动三轴-空心圆柱扭剪试验机对不同应力路径下的非饱和黄土的累计塑性变形问题进行了研究[11]。

综上，已有研究对动荷载作用下岩石的变形及破坏机制较为详细，但对不同影响因素的分析较少。基于此，本文在总结前人成果的基础上，结合沈阳地铁四号线的工程实际，对饱和中风化粉砂岩进行动三轴试验研究，分析不同影响因素对试样的作用机制，为工程实际提供可靠的理论依据。

1 试验介绍

1.1 试验设备

本文地铁隧道围岩动三轴试验均在英国进口的GDS多功能三轴试验系统上进行，该设备具有轴向、围压、孔隙水压等多套相互独立的控制系统。可实现正弦波、余弦波、半正弦波的动态加载方式，加载频率在0～2 Hz范围内。最大轴向压力为10 kN，最大围压为2 MPa，最大轴向位移为20 mm。加载方式有应力和应变两种控制方法，试样在经历加—卸—加载过程所产生的变形即为累积塑性应变。

1.2 试样制备

本文试验用地铁隧道围岩取自沈阳地铁四号线某站基底中风化砂岩。通过钻孔取芯，将钻取的岩样用塑料膜包裹，防止因水分蒸发而导致开裂。本文中风化砂岩取样深度约为35～40 m，外表呈灰白色，节理裂隙较为发育。运至室内试验室，经过切割、打磨，最终制得直径39.1 mm、高80 mm的标准圆柱体。通过岩石力学检测试验，得到本文试验用中风化砂岩的基本物理力学参数见表1。

表1 基本物理力学参数

1.3 试验方案

首先将试样放入真空饱和箱中预饱和，之后GDS三轴试验系统中进行充分饱和，最后对饱和试验进行固结排水，当超孔隙水压与反压相等时，固结完成，施加动应力和静偏应力。

为模拟地铁车辆荷载，采用三种动态加载方式进行三轴试验，根据试验数据与实测数据对比结果可知，半正弦波加载方式所获取的试验数据与地铁隧道实测数据更为接近，因此本文采用单向等幅的半正弦波来模拟地铁列车荷载。沈阳地铁设计时速为80 km/h，单节车厢重约14 t，动应力比计算方法见式(1)。由于本文中风化粉砂岩取自埋深约35～40 m处，因此本文选取围压分别为400、500、600和700 kPa。根据现场监测数据，列车经过时不同的速度会导致不同频率，其中低频约0.5～0.7 Hz，高频约2.4～2.7 Hz，因此本文加载频率取0.5、1、1.5和2.5 Hz。根据已有研究成果可知，岩石类材料的偏应力越大，达到破坏的时间越短，因此，本文取静偏应力分别为0、50、100、150 kPa进行试验，静偏应力比计算方法见式(2)。本文中风化粉砂岩的静偏应力比、动应力比见表2。

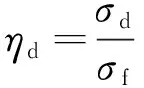
(1)

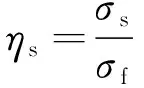
(2)

式中：ηd为动偏应力比；σd为动应力幅值，MPa，σd=0.26m×(1±0.004)v，m为列车轴重，kg，v为行车速度，m/s；σf为静极限强度，MPa；ηs为静偏应力比；σs为静偏应力，MPa。根据上述试验参数的确定方法，本文试验方案见表2。

表2 试验方案

2 试验结果分析

2.1 静偏应力比作用分析

为分析不同静偏应力比作用下中风化砂岩的累计塑性变形问题，根据表2，采用控制变量法进行试验研究，即保持动应力比、加载频率及围压不变，通过改变静偏应力比来分析其影响机制。

图1(a)为不同静偏应力比下中风化粉砂岩的累计塑性应变随加载循环次数的演化曲线，由图可知，当静偏应力比为0.369时，累计塑性应变曲线表现为稳定型，即随着加载循环次数的逐渐增大，曲线斜率逐渐减小，且逐渐趋于某一恒定值，试样未发生破坏；当静偏应力比为0.5时，累计塑性应变曲线表现为非稳定型，即随着加载循环次数的逐渐增大，曲线斜率开始呈逐渐减小变化趋势，当加载循环次数达到一定值时，曲线斜率逐渐增大，累计塑性变形迅速增大，试样破坏。图1(b)为加载循环600次对应的累计塑性应变随静偏应力比分布曲线，由图可知，累计塑性应变与静偏应力比呈指数函数递增关系，当静偏应力比为0时，累计塑性应变为0.386%，当静偏应力比为0.369时，累计塑性应变为0.728%，较静偏应力比为0时增长了约88.6%，而此时累计塑性应变演化曲线仍表现为稳定型；当静偏应力比为0.5时，累计塑性应变为2.038%，较静偏应力比为0时增长了约427.98%，可见，静偏应力比的增大使得岩样的损伤程度明显加重。原因是饱和中风化砂岩内部颗粒间的胶结作用受到破坏，黏结能力下降，在循环加—卸载作用下，试样内部原始微缺陷、微裂隙不断扩展，导致试样劣化程度逐渐加重，当静偏应力比增大至某一值时，试样内部裂隙相互贯通，形成宏观裂缝，失稳破坏。根据本文研究可知，中风化粉砂岩的临界静偏应力比在0.369～0.5之间。

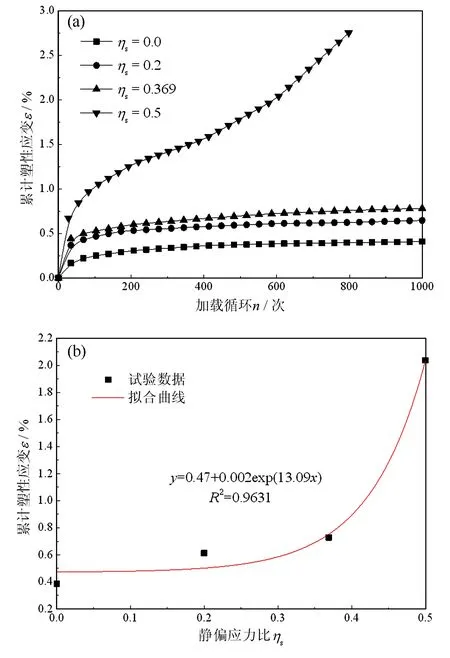
图1 不同静偏应力比累计塑性应变演化曲线

2.2 动应力比作用分析

为分析不同动应力比作用下中风化砂岩的累计塑性变形问题，根据表2，采用控制变量法进行试验研究，即保持静偏应力比、加载频率及围压不变，通过改变动应力比来分析其影响机制。

图2(a)为不同动应力比下中风化粉砂岩的累计塑性应变随加载循环次数的演化曲线，由图可知，当动应力比小于0.048时，累计塑性应变曲线表现为稳定型；当动应力比为0.07时，累计塑性应变曲线表现为非稳定型。不同动应力比下累计塑性应变曲线的变化趋势与不同静偏应力类似。图2(b)为加载循环600次对应的累计塑性应变随动应力比分布曲线，由图可知，累计塑性应变与动应力比呈指数函数递增关系，当动应力比为0.024时，累计塑性应变为0.546%，当动应力比为0.048时，累计塑性应变为0.897%，较动应力比为0.024时增长了约64.29%，而此时累计塑性应变演化曲线仍表现为稳定型；当动应力比为0.07时，累计塑性应变为1.803%，较动应力比为0.024时增长了约230.22%，可见，动应力比的增大使得岩样的损伤程度明显加重。原因是饱和中风化砂岩与未风化砂岩相比，其内部裂隙相对较多，颗粒间胶结作用较弱，当动应力达到某一值时，试样发生失稳破坏。根据本文研究可知，中风化粉砂岩的临界动应力比在0.048～0.07之间。

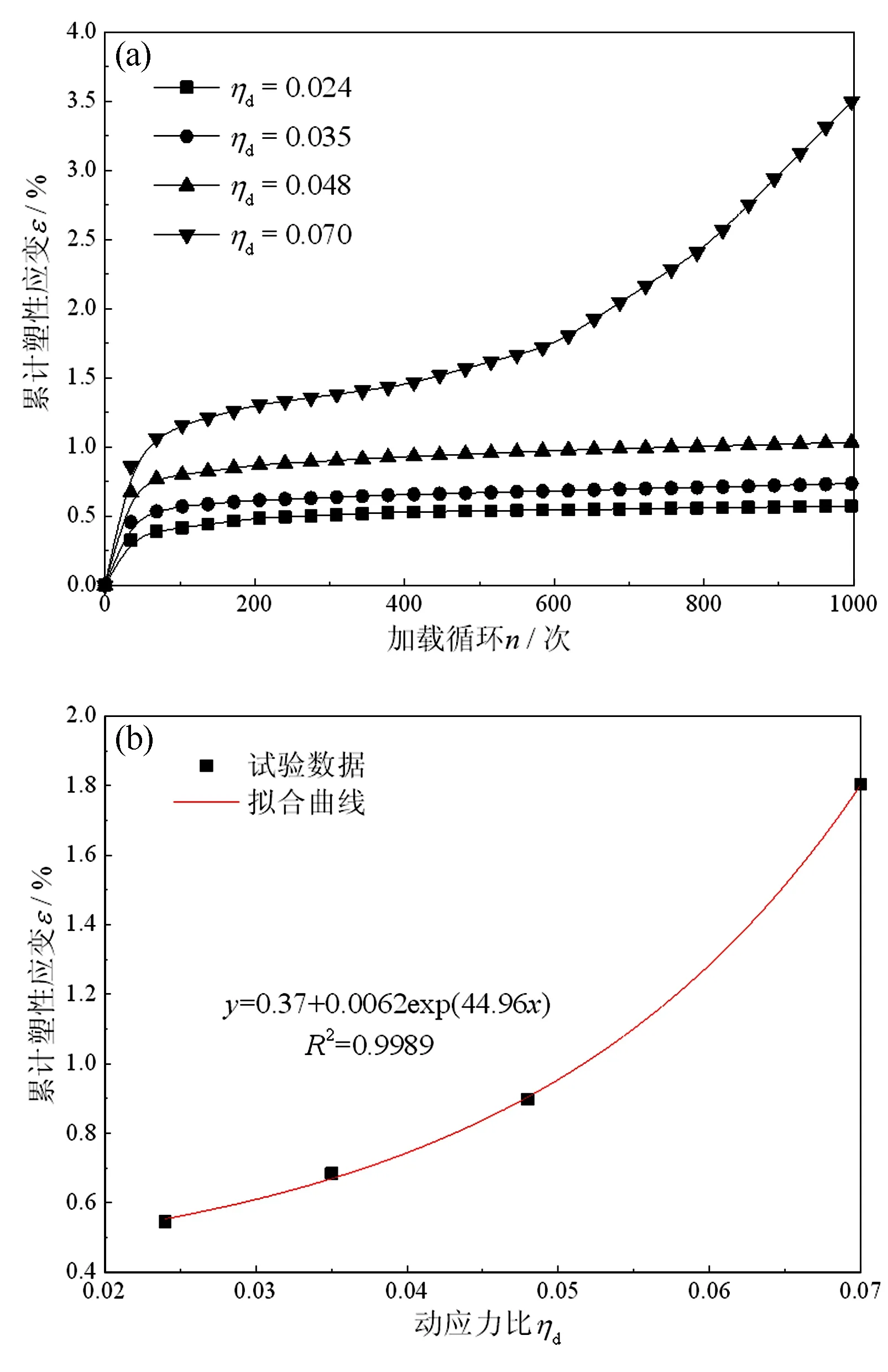
图2 不同动应力比累计塑性应变演化曲线

2.3 加载频率作用分析

为分析不同加载频率作用下中风化粉砂岩的累计塑性变形问题，根据表2，采用控制变量法进行试验研究，即保持静偏应力比、动应力比及围压不变，通过改变加载频率来分析其影响机制。

图3(a)为不同加载频率下中风化粉砂岩的累计塑性应变随加载循环次数的演化曲线，由图可知，不同加载频率下，中风化粉砂岩的累计塑性应变曲线均表现为稳定型，试样未发生破坏。图3(b)为加载循环600次对应的累计塑性应变随加载频率分布曲线，由图可知，累计塑性应变与加载频率之间呈线性函数递减关系，当加载频率为0.5 Hz时，累计塑性应变为0.995%，当加载频率为2.0 Hz时，累计塑性应变为0.496%，加载频率由0.5 Hz增至2.0 Hz，累计塑性应变减小了约50.15%，可见，加载频率的增大使得岩样的损伤程度减轻。原因可解释为，当加载频率较小时，荷载作用在试样上的时间更长，进而使得裂隙充分发育，损伤加重，累计塑性变形增大。

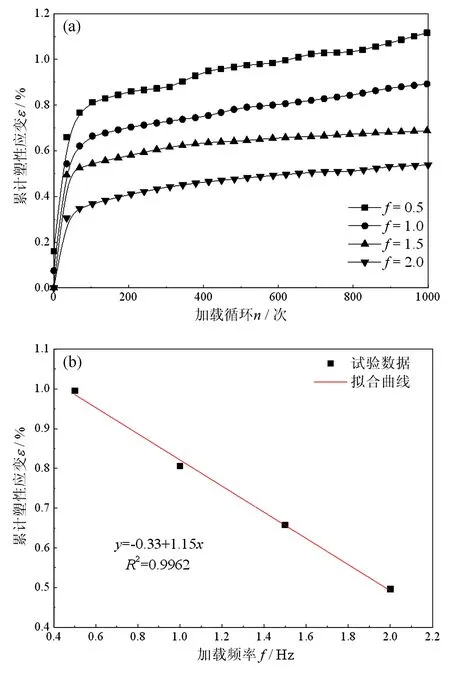
图3 不同动应力比累计塑性应变演化曲线

2.4 围压作用分析

为分析不同围压作用下中风化粉砂岩的累计塑性变形问题，根据表2，采用控制变量法进行试验研究，即保持静偏应力比、动应力比及加载频率不变，通过改变围压来分析其影响机制。

图4(a)为不同围压下中风化粉砂岩的累计塑性应变随加载循环次数的演化曲线，由图可知，不同围压下，中风化粉砂岩的累计塑性应变曲线均表现为稳定型，试样未发生破坏。图4(b)为加载循环600次对应的累计塑性应变随围压分布曲线，由图可知，累计塑性应变与围压之间呈线性函数递减关系，当围压为400 kPa时，累计塑性应变为0.844%，当围压为700 kPa时，累计塑性应变为0.437%，围压由400 kPa增至700 kPa，累计塑性应变减小了48.22%，可见，围压的增大使得岩样的损伤程度明显减轻。原因是围压作用下，饱水中风化粉砂岩内部孔隙和缺陷重新排列，内部颗粒间更加密实，进而使得试样的整体性能等到提升，累计塑性变形减小。

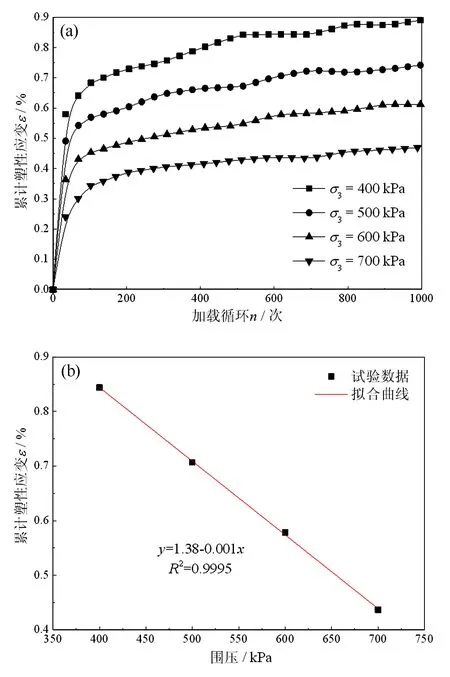
图4 不同动应力比累计塑性应变演化曲线

3 结论

(1)随着加载循环次数的逐渐增大，当静偏应力比为0.369时，累计塑性应变曲线表现为稳定型；当静偏应力比为0.5时，累计塑性应变曲线表现为非稳定型。累计塑性应变与静偏应力比呈指数函数递增关系。

(2)随着加载循环次数的逐渐增大，当动应力比小于0.048时，累计塑性应变曲线表现为稳定型；当动应力比为0.07时，累计塑性应变曲线表现为非稳定型。累计塑性应变与动应力比呈指数函数递增关系。

(3)随着加载循环次数的逐渐增大，不同加载频率下中风化粉砂岩的累计塑性应变曲线均表现为稳定型。累计塑性应变与加载频率之间呈线性函数递减关系。

(4)随着加载循环次数的逐渐增大，不同围压下中风化粉砂岩的累计塑性应变曲线均表现为稳定型。累计塑性应变与围压之间呈线性函数递减关系。