基于对称逐步超松弛的低复杂度信道估计算法

王 彬，谢 杰，陈 麟

（1中科芯集成电路有限公司，江苏 无锡 214072；2中国电子科技集团公司第五十八研究所，江苏 无锡 214072）

0 引 言

随着无线设备接入量和数据需求的急剧增长，为每一个用户终端提供足够的频谱资源和容量无疑成为对基站通信技术的巨大挑战。如今，在大规模多输入多输出（Multiple-Input Multiple-Output，MIMO）系统中，基站端的天线数量远大于所服务的用户数量，实现了同一时间和频率资源下，拥有更高的频谱效率，可同时服务于数十个移动用户。因此，大规模MIMO技术被视为未来无线通信系统的关键技术之一。

信道估计是大规模MIMO系统的重要部分，精确的信道状态信息对于基站而言尤为关键。传统的最小均方误差（Minimum Mean Square Error，MMSE）信道估计算法可以实现较优的性能，但其涉及到高维矩阵的求逆运算，增加了系统实现的复杂度。近些年来，越来越多的研究开始关注信道估计技术，如：文献［3］提出了一种低复杂度级数展开算法来避免矩阵求逆，降低了系统计算复杂度，但计算涉及复杂的参数优化问题，使得复杂度又逐渐升高；文献［4］提出了一种迭代信道估计算法，减少导频污染的影响；文献［5］提出了一种基于压缩感知辅助的信道估计算法，可最大化利用信道的空间共稀疏性。随着近几年深度学习技术的逐渐成熟，信道估计应用于无信通信系统领域成为可能，越来越多的研究人员开始将深度学习与通信系统相结合，以解决更加复杂的问题，提高系统智能化。为了处理大规模MIMO系统复杂的空间结构问题，文献［6］提出了一种新的框架，将深度学习与大规模MIMO系统相结合以提高系统性能。

上述方法在降低系统计算复杂度与保证系统性能等方面难以达到有效平衡，因此，研究新的信道估计算法具有重要意义。

为降低大规模MIMO系统的计算复杂度，保证算法与复杂度之间的有效平衡，本文提出了一种基于对称逐步超松弛（Symmetric Successive Over Relaxation，SSOR）的信道估计算法，该方法可有效避免矩阵求逆运算，降低了系统计算复杂度；根据大规模MIMO系统中信道矢量渐近正交的相关特性，进一步提高SSOR算法的稳定性；最后，对所提算法进行了仿真实验对比分析，结果表明该算法可有效降低系统复杂度，且随着迭代次数的增加，其性能逐渐接近于MMSE算法，较好地实现了低复杂度与高性能之间的有效平衡。

1 典型系统模型

典型的大规模MIMO上行链路系统，假设其工作于时分双工模式，基站端装配有N根天线，并同时服务于N个单天线用户，且基站端天线数远大于用户数。向量∈ℂ表示用户发送信号，信道矩阵∈ℂ表示平坦瑞利衰落信道，且满足分布(0，1)。在基站端，接收信号∈ℂ的表达式为式（1）：

其中，向量∈ℂ表示复高斯白噪声，满足分布(0，)。

2 基于SSOR迭代的低复杂度信道估计算法

2.1 基于MMSE的信道估计算法

用户向基站发送导频信号，基站端的接收信号表示为式（2）：

其中，矩阵∈ℂ表示为信道的协方差矩阵，矩阵为厄尔米特正定矩阵。

由式（4）可知，基于MMSE的信道估计涉及到高维矩阵的求逆运算，其复杂度( )（其中M＝N×N），随着大规模MIMO系统天线数的增加而迅速增大，不利于硬件系统的实现。

2.2 基于SSOR的信道估计算法

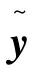
（1）将矩阵分解得式（5）：

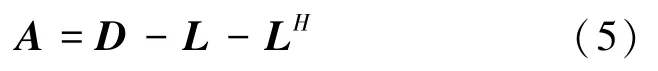
其中，矩阵、、L分别表示由矩阵中的元素所组成的对角矩阵、严格下三角矩阵和严格上三角矩阵。

（2）一次SSOR迭代是由两个半个SOR迭代组成，而采用SOR迭代计算第一个半迭代，可得式（6）：

（3）采用SOR迭代计算第二个半迭代为式（7）：

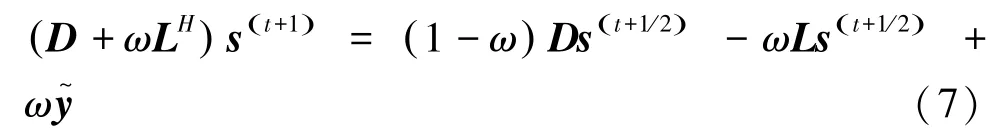
在式（6）和式（7）中，表示松弛因子参数，且02，松弛因子影响着SSOR算法的收敛性能，其与算法的收敛性相关，表示迭代次数。

在基于式（6）～（7）的多次迭代后，得到的向量，即可近似为A y的值，因此可以有效避免矩阵的求逆运算。

2.3 松弛因子和复杂度分析

基于SSOR的预编码可以在不损失性能的情况下将经典ZF预编码的复杂性降低约一个数量级，并且在典型衰落通道中的表现也优于线性近似预编码方案。因此，对于SSOR迭代法，其最优松弛因子ω的取值为式（8）：

对于大规模MIMO系统而言，基于随机矩阵理论，矩阵D可近似为(1／N I)，则矩阵的频谱半径可近似为式（10）：

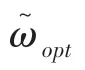
对于基于SSOR的信道估计算法，其复杂度主要来源于式（6）～（7）的迭代计算，将式（6）～（7）转化为方程（12）～（13）：

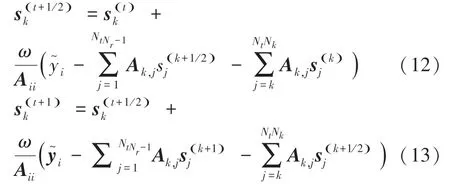
其中，下标参数表示向量或矩阵的第个元素。

由式（12）可知，计算此部分所需要的复数乘法次数为次，综合式（12）～（13）可得其计算复杂度为( 12)。

3 仿真结果比较分析

采用归一化的均方误差来评估本文所提出的SSOR算法的性能，且将传统的MMSE算法作为基础比较。考虑典型的大规模MIMO上行链路系统，假设其基站装配有N＝100根天线，服务于N＝10个单天线用户，导频序列的长度为10，为导频污染因子。

无导频污染，即0的情况下，比较了基于SOR迭代、基于SSOR迭代以及基于MMSE的3种信道估计算法在不同迭代次数下的归一化均方误差性能，如图1所示。由图1可知，随着迭代次数的增加，基于SSOR迭代的信道估计算法的性能趋近于基于MMSE的信道估计算法，且基于SSOR迭代的信道估计算法性能优于基于SOR迭代的信道估计算法，收敛速度更快。

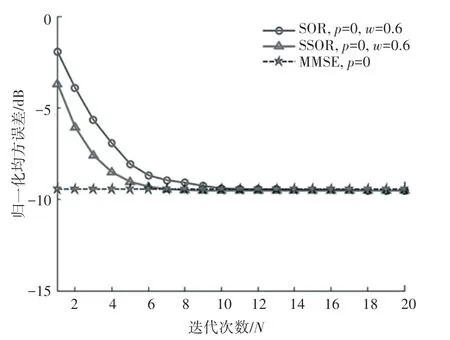
图1 无导频污染不同迭代次数下的归一化均方误差Fig.1 Normalized mean square error under different iteration times without pilot pollution

在导频污染0.1的情况下，比较了基于SOR迭代、基于SSOR迭代以及基于MMSE的3种信道估计算法在不同迭代次数下的归一化均方误差性能，如图2所示。由图2可知，存在导频污染的情况下，基于SOR迭代的信道估计算法和基于SSOR迭代的信道估计算法的归一化均方误差均随着迭代次数的增加而逐渐达到收敛，SSOR迭代信道估计算法的收敛速度更快，且更接近基于MMSE的信道估计算法。

图2 有导频污染不同迭代次数下的归一化均方误差Fig.2 Normalized mean square error under different iteration times with pilot pollution

4 结束语

为避免高维矩阵的直接求逆运算，降低大规模MIMO系统信道估计算法的复杂度，本文主要研究了一种基于SSOR迭代的低复杂度信道估计算法，并分析了最优松弛因子的选择，得出了最优松弛因子只与天线数量有关的结论。经仿真实验表明，该算法的计算复杂度相比于传统的MMSE算法降低了一个数量级，且随着迭代次数的增加，其性能接近于MMSE算法。综合上述分析，本文所提出的算法可有效实现低复杂度和高性能之间的平衡。