考虑执行器响应时滞的磁流变悬架H2/H∞鲁棒控制研究

孙 东， 汪若尘， 丁仁凯， 刘 伟， 孟祥鹏

(1.江苏大学 汽车与交通工程学院，江苏 镇江 212013;2.江苏大学 汽车工程研究院，江苏 镇江 212013)

为解决传统被动悬架因刚度阻尼固定不变而只能在某一运行工况下达到性能最优这一车辆动力学问题，主动/半主动悬架应运而生[1-4]。而随着磁流变技术的发展与成熟，响应快、成本低、控制简单、安装方便的磁流变半主动悬架[5-8]更受市场青睐。但半主动悬架系统不可避免地存在工作时滞[9-10]，其中，磁流变阻尼器的响应时滞占据很大一部分比重。这不仅会削弱控制系统的控制效果，甚至有可能使悬架系统动力学性能恶化，造成被控对象失稳[11-13]。

为此，学者们对半主动悬架系统时滞补偿控制展开了广泛研究。寇发荣[14]根据包含执行器响应时滞的线性常微分方程理论推导了磁流变半主动悬架的临界时滞，设计了一种Smith 预估时滞补偿模糊控制器，仿真和试验结果均证明了该控制器可明显改善时滞输入下的车辆动力学性能。Huang等[15]针对二自由度时滞非线性悬架系统模型，设计了一种鲁棒性强的PID控制策略，并采用遗传算法对PID控制器进行了参数优化，仿真结果表明车辆的综合性能得到了显著提高。陈士安等[16]提出了一种泰勒级数-LQG时滞补偿控制方法，利用泰勒级数对LQG计算得到的理想控制力进行时滞补偿，这种控制方法使悬架系统即使在较大时滞下也能保持较好的平顺性。Dong等[17]构建了一种悬架系统神经网络模型，用以补偿磁流变阻尼器的不确定时延，试验结果表明，基于SMIS的半主动悬架具有更好的乘坐舒适性，还可有效避免执行器时滞不确定性对车辆动力学性能的恶化作用。

磁流变阻尼器响应时滞输入会对闭合控制系统的控制效果及稳定性造成负面影响，常见的解决办法是设计状态反馈控制器进行时滞控制，但当前研究鲜有考虑执行器实际响应时滞与系统失稳的临界时滞之间的大小关系，即总是假设实际时滞小于临界时滞。一旦前者数值超过后者，控制器将无法求得反馈增益而失效。针对这一问题，本文设计一种时滞H2/H∞鲁棒控制器，推导控制器反馈控制增益和系统临界时滞，并基于MotoTron平台搭建执行器驱动电流PI控制器，旨在降低实际响应时滞以实现时滞输入鲁棒控制。

1 磁流变半主动悬架系统建模

1.1 磁流变阻尼器力学模型

Meisami-Azad等[18-21]采用的磁流变阻尼器Bingham黏塑模型将阻尼器控制力分为仅与速度相关的黏滞阻尼力和与驱动电流相关的库仑阻尼力，表达式如下

(1)

式中:F(t)为阻尼器控制力；ce为黏滞阻尼系数；v为悬架相对速度；FMR为库伦阻尼力；ai为待拟合参数；I为驱动电流。

为获取模型参数，在单通道试验台上对磁流变阻尼器进行力学试验，台架布置如图1所示。

图1 阻尼器力学试验台架布置

依据测得的试验数据，采用MATLAB的Curve Fitting工具箱进行参数辨识，具体参数值如表1所示。图2为磁流变阻尼器速度特性曲线拟合效果图，从图中可看出，式(1)曲线与试验数据曲线吻合度较高，说明Bingham黏塑模型能较好地描述磁流变阻尼器力学特性。

表1 参数辨识结果

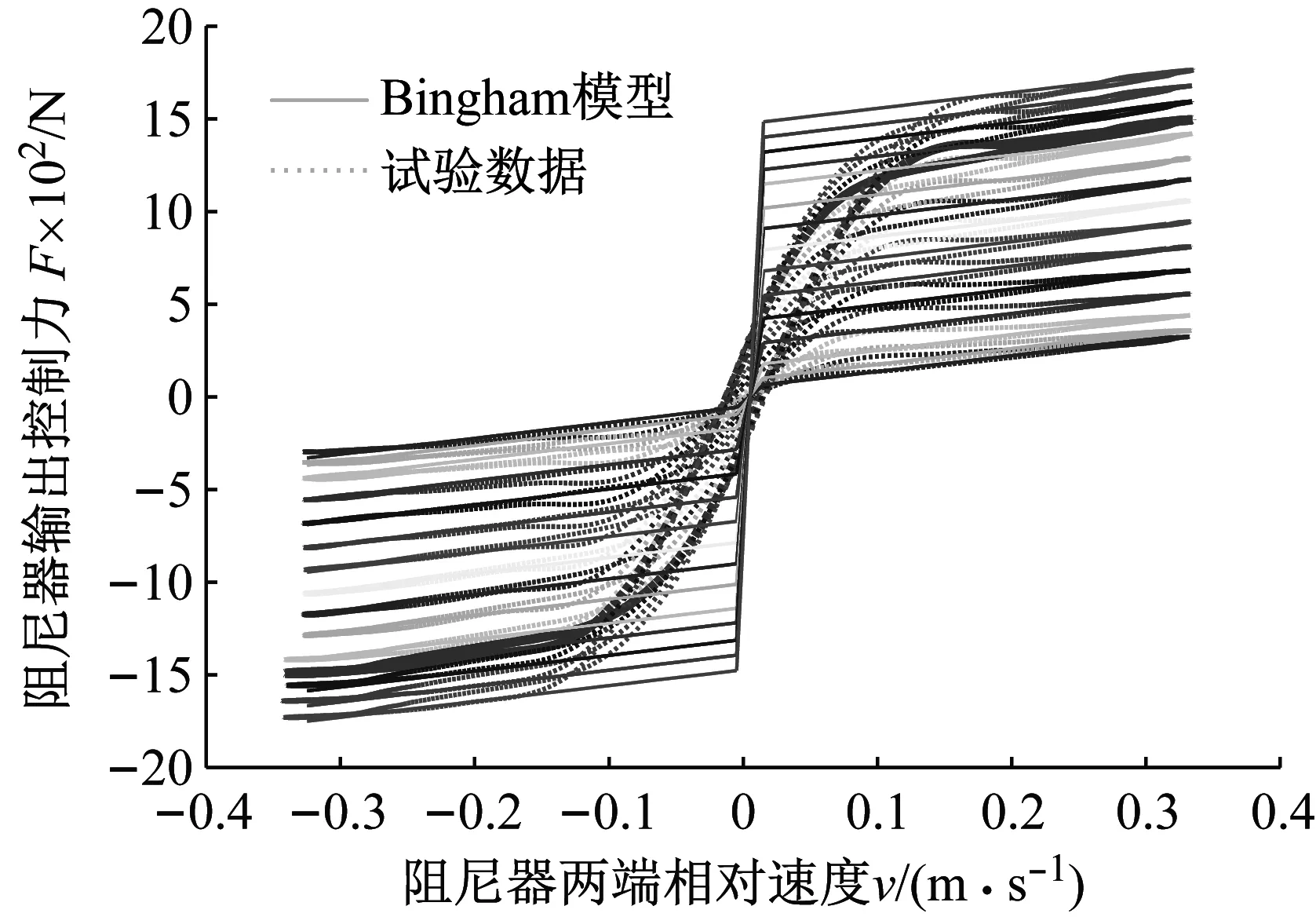
图2 阻尼器速度特性曲线拟合效果

1.2 1/4时滞输入磁流变半主动悬架模型

定常输入时滞作用下的1/4时滞输入磁流变半主动悬架的二自由度模型如图3所示，根据牛顿第二定律得到平衡位置处的悬架动力学微分方程

(2)

图3 1/4时滞输入磁流变半主动悬架模型

其中，

式中:ms为簧载质量；mu为非簧载质量；ks为悬架弹簧刚度；ku为轮胎刚度；u(t-τ)磁流变阻尼器时滞输出力；zs为簧载质量垂向位移；zu为非簧载质量垂向位移；zr为路面激励。

1.3 悬架系统状态空间表示

对于上述半主动悬架系统，选取状态变量为

(3)

选取输出变量为

(4)

测量变量为

Z(t)=X(t)

(5)

因此，式(2)悬架动力学微分方程的状态空间可表示为

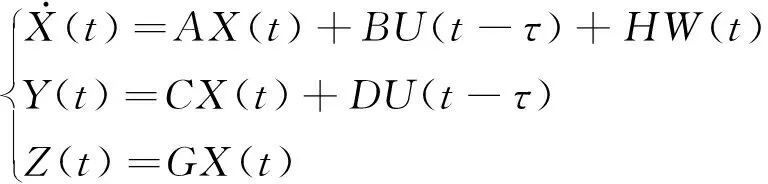
(6)

2 时滞H2/H∞鲁棒控制器设计

H2控制器用于约束时滞控制力以实现悬架综合性能最优，而H∞控制器用于约束下一时滞时刻的控制力以控制定常输入时滞，进而保证悬架系统的控制性能和系统稳定性。在设计定常输入时滞半主动悬架系统的输出反馈控制律之前，先设置如式(7)所示的悬架综合性能指标作为控制目标。

(7)

时滞H2/H∞鲁棒控制器的设计就是使从路面输入(t)到系统输出Y(t)的传递函数的H2和H∞范数最小，从而保证定常输入时滞半主动悬架的最优综合性能和系统稳定性。反馈控制律的具体形式为

U(t)=KZ(t)=KX(t)

(8)

式中，K为状态反馈增益矩阵。

因此，式(6)可表示为如下闭环系统

(9)

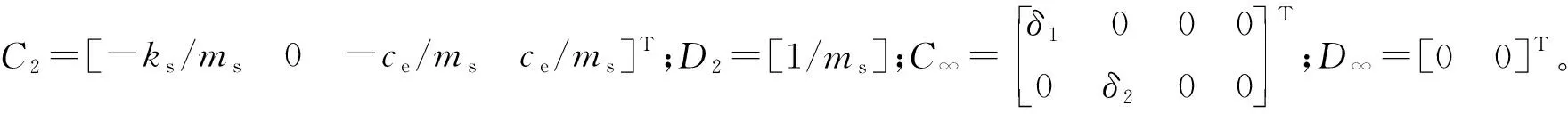
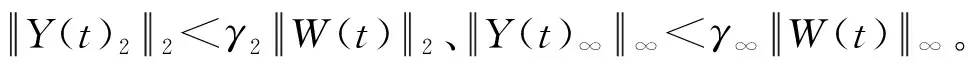
定理1给出了时滞H∞鲁棒控制器存在的充要条件：

(10)

(11)

式中:S=LAT+AL+τP+Q+QT+N;I为适当维数的单位矩阵。

下面构造一个Lyapunov-Krasovskii泛函V(t)进行证明

V(t)=V1(t)+V2(t)+V3(t)

(12)

式中:V1(t)=XT(t)P1X(t)；

其中，待求矩阵P1、Q1、Q2正定对称。

对式V1(t)进行一阶微分，得：

(13)

引理1[23]若向量a(·)∈Rm,b(·)∈Rm,N1∈Rm×n定义在区间Ω内，则对于∀X1、Y1、Z1∈Rm×n，满足下式关系

(14)

τXT(t)X1X(t)+XT(t)(Y1-P1BK)X(t)-

XT(t)(Y1-P1BK)X(t-τ)+XT(t)(Y1-P1BK)TX(t)-

(15)

由式(13)～(15)可得

XT(t)(P1BK-Y1)X(t-τ)+

XT(t-τ)(P1BK-Y1)TX(t)+T(t)HP1X(t)+

(16)

零初始条件下的时滞系统H∞鲁棒性性能指标如下

(17)

对于任意非零输入可得

(18)

式中：λ(t)=[X(t),X(t-τ),(t)]T；

Γ5=τKTBTQ1H；

Γ3=τATQ1H+P1H；

由Schur补可知，П<0与下式等价

(19)

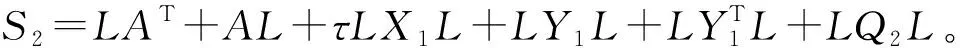
式(11)中含有非线性项LM-1L，故悬架系统的渐进稳定问题转化为带矩阵逆约束的线性矩阵不等式可行性问题。本文综合考虑悬架动力学性能，参考抗干扰系数和系统鲁棒性的博弈关系，在选定抗干扰系数γ∞=12.5基础上，采用锥补线性化迭代法和二分法[24]求解保持系统稳定的临界时滞为τmax=29.2 ms，为执行器驱动电流PI控制提供理论基础。

3 仿真分析对比

3.1 磁流变阻尼器时滞测试

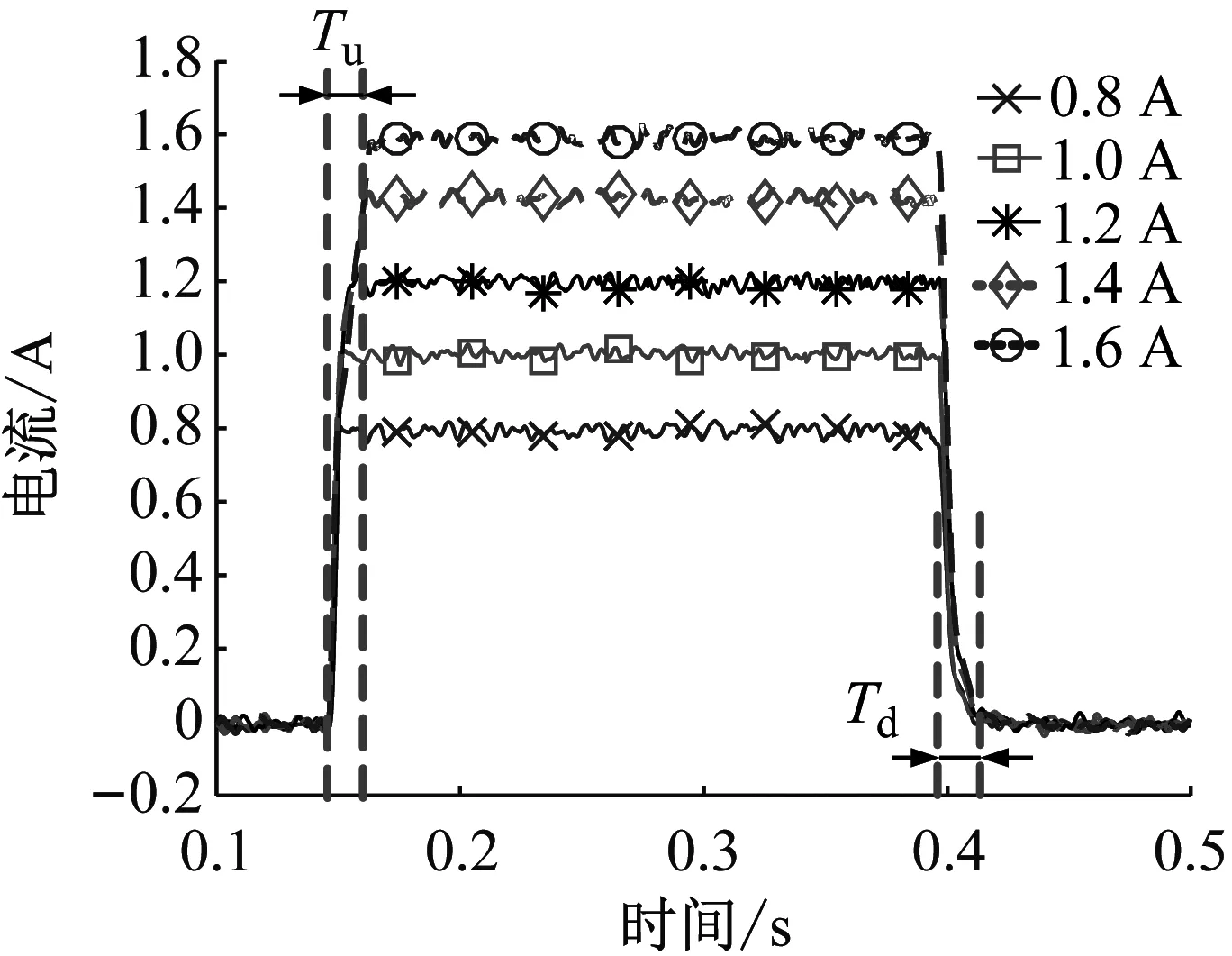
求解时滞H2/H∞鲁棒控制器反馈增益的前提是确定系统响应时滞与抗干扰系数，当磁流变阻尼器的实际响应时滞超出理论临界时滞时，系统将处于失稳状态，此时无法获得控制器的反馈增益。为了验证所设计的时滞H2/H∞鲁棒控制器应用于磁流变半主动悬架系统的可行性，本文进行了执行器开环系统响应时滞测试，测试工况选择频率2 Hz、占空比50%的方波，响应特性如图4所示。

(a) 阶跃响应

从图4中可看出，执行器驱动电流上下阶跃的响应时滞都大于35 ms，已超过理论临界时滞，此时时滞H2/H∞鲁棒控制器无法求解反馈增益。为此，本文引入驱动电流积分分离PI控制[25]来改善执行器开环响应特性，减小系统时滞，进而保证时滞H2/H∞鲁棒控制器正常工作。

3.2 驱动电流PI控制算法

积分分离PI控制离散后的表达式如下

(20)

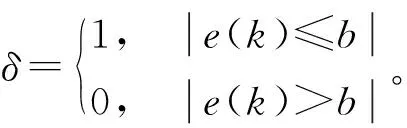
其中，b为积分项启闭阈值，其数值的选取直接影响PI控制的控制效果。

本文基于MotoTron平台采用试凑法对PI控制的三个控制参数Kp、Ki和b进行工程整定，搭建了如图5所示PI控制参数整定平台，整定结果如图6所示。

图5 PI控制参数整定平台

(a) 阶跃响应

由图6可知，PI控制下的执行器响应时滞都减小到16 ms以内，低于系统保持稳定所允许的理论临界时滞。将控制结果代入时滞H2/H∞鲁棒控制器设计过程，采用锥补线性化迭代算法和最小二乘法，求得时滞H2/H∞鲁棒控制器的可行解为K=104×[1.500 7 1.609 1 -0.154 1 -0.004 0]。

4 仿真分析

为验证所设计的时滞H2/H∞鲁棒控制器的工作效果，在Matlab/Simulink中搭建了1/4被动悬架和不考虑时滞输入的H2/H∞鲁棒控制器模型作为对比，以60 km/h车速进行了C级随机路面仿真，仿真参数如表2所示。

表2 1/4车辆仿真参数

时滞H2/H∞鲁棒控制器和不考虑时滞控制的鲁棒控制器的仿真结果如图7和表3所示，由悬架动力学性能评价指标时域响应曲线可看出，在以乘坐舒适性为主要控制目标的C级路面下，对执行器响应时滞进行控制的时滞鲁棒控制器可显著改善车身加速度(减小了24.52%)，而未考虑时滞的鲁棒控制器优化效果有限，相比被动悬架仅优化了14.94%；时滞H2/H∞鲁棒控制器下的悬架动挠度较被动悬架降低了9.79%，比鲁棒控制器还优化了7.19%；而轮胎动载荷比被动悬架恶化了9.80%，由于并未超过车辆静载重量的1/3，因而不会影响车轮接地性，但其相比恶化了13.44%的鲁棒控制器，考虑了执行器时滞输入的时滞H2/H∞鲁棒控制器更能兼顾车辆的乘坐舒适性和行驶安全性。

图7 悬架仿真结果对比

表3 仿真结果均方根值对比

5 台架试验

为进一步验证时滞H2/H∞鲁棒控制器的实际工作效果，设计了磁流变半主动悬架ECU，时滞鲁棒控制器采用基于模型设计(MBD)方法内嵌到ECU中。并搭建了如图8所示的单轮连杆式麦弗逊悬架测控平台，对控制器进行了台架试验，试验工况与仿真相同。

图8 台架试验布置

图9为悬架系统在被动状态、鲁棒控制器和时滞H2/H∞鲁棒控制器下的动力学性能时域响应，表4列举了三个评价指标的均方根值。从表中数据可知，时滞H2/H∞鲁棒控制器的车身加速度和悬架动挠度相比被动悬架和鲁棒控制器分别降低了17.17%、9.84%、6.42%和5.98%，说明在颠簸的C级路面下，时滞H2/H∞鲁棒控制器能有效抑制车身加速度，悬架动挠度的降低也减小了悬架撞击到缓冲块的几率，车辆乘坐舒适性得到明显改善。此时轮胎动载荷虽有所恶化，但并未影响轮胎接地性。这也证明了所设计的时滞H2/H∞鲁棒控制器能对执行器响应时滞进行控制，保证了时滞输入悬架系统的控制性能和稳定性。

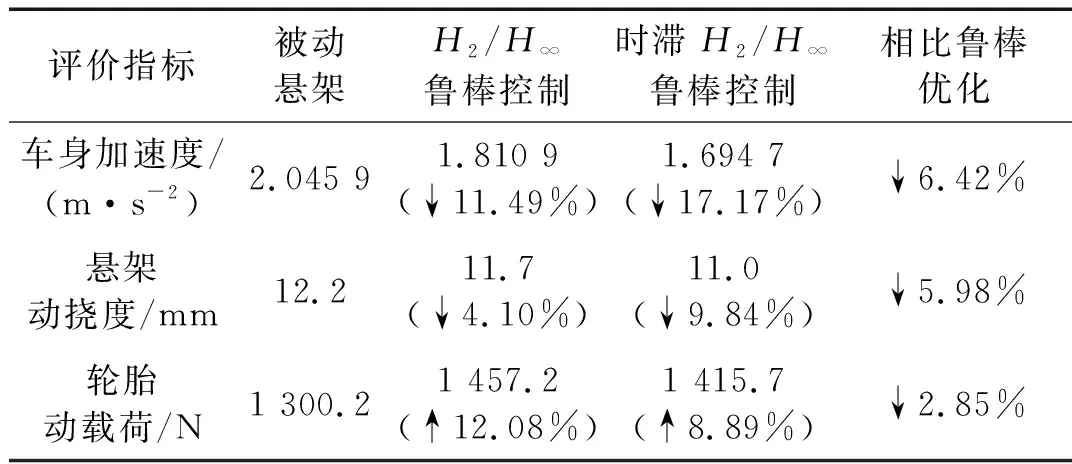
表4 试验结果均方根值对比

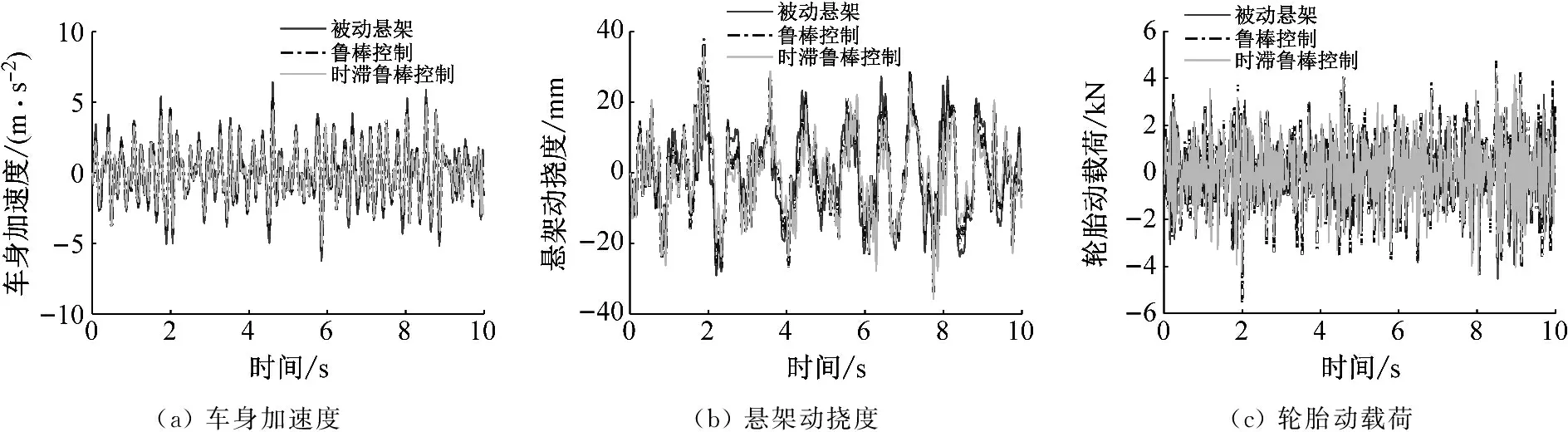
图9 悬架试验结果对比

6 结 论

(1) 基于磁流变阻尼器Bingham模型，针对执行器响应时滞的问题，设计了一种时滞H2/H∞鲁棒控制器，推导了控制器反馈控制增益和系统临界时滞，并基于MotoTron平台整定了执行器驱动电流PI控制参数，从而降低了实际响应时滞以实现时滞鲁棒控制。

(2) 在C级随机路面输入下对1/4时滞输入磁流变半主动悬架系统进行了仿真分析，结果表明，时滞H2/H∞鲁棒控制器相比被动悬架，车身加速度和悬架动挠度分别降低了24.52%和9.79%，相比不考虑时滞控制的鲁棒控制器还优化了11.26%和7.19%，证明了时滞H2/H∞鲁棒控制器能保证时滞输入系统的控制性能和稳定性。台架试验结果也验证了控制器的有效性。