波动温度环境下形状记忆合金梁的参激振动控制
王龙飞, 崔 璐, 韩志军, 吴 莹
(1. 太原理工大学 生物医学工程学院, 太原 030024; 2. 太原理工大学 信息化管理与建设中心, 太原 030024;3. 西安交通大学 航天航空学院机械结构强度与振动国家重点实验室, 西安 710049)
形状记忆合金是一种材料刚度可以随温度变化而发生改变的温敏性材料,其广泛应用于汽车工业、航天航空和生物医学工程等领域,是近年来比较热门的智能材料之一[1-3]。根据已有的试验观测可知,形状记忆合金在温度影响下会发生马氏体相变或逆马氏体相变,材料的微观结构会在马氏体和奥氏体之间发生转变,进而影响合金的宏观物理性质[4]。基于此,可以利用改变温度控制形状记忆合金结构的振动。
Hashemi等[5]曾研究了两端简支的超弹性形状记忆合金梁在不同温度条件下的自由振动,发现通过改变温度可以控制梁的振动;Damanpack等[6]研究了冲击载荷下形状记忆合金层合梁的振动控制,揭示了可受温度调控的非孪晶马氏体体积分数对层合梁阻尼效应的影响;Savi等[7]和Piccirillo等[8]分别研究了形状记忆合金结构的非线性振动,其结果表明通过改变温度可以使结构的振动状态在定常态和混沌态之间相互转变;Han等[9]通过稳定性和分岔理论具体解释了系统运动状态变化的原因,并强调了温度的重要影响;利用前述研究,Fu等[10]和Costa等[11]分别实现了通过改变温度对干摩擦形状记忆合金振子系统和复杂形状记忆合金单摆系统的振动控制。
目前对形状记忆合金结构的振动控制主要是通过单调改变温度来实现的。根据Xia等[12]的试验研究可知,温度诱发的形状记忆合金相变可以在很短的时间内发生(一次相变循环约为0.8 s),因此合金的力学性能也可以短时间发生变化。基于此,本文考虑温度为变参数,研究了形状记忆合金梁在波动变化的温度场中的参数激励振动控制。
1 控制方程
如图1所示,一端固支一端夹支的形状记忆合金梁,其尺寸分别为有效跨长L、梁宽b和梁高h。合金梁在横向上受周期性扰动力的作用,该扰动力可以表示为P=P1+δcosωt,其中P1和δ表示控制参数,ω表示周期性扰动力的频率。若不考虑轴向力和阻尼作用,由Euler-Bernoulli梁理论可得合金梁的横向振动方程,如下
(1)
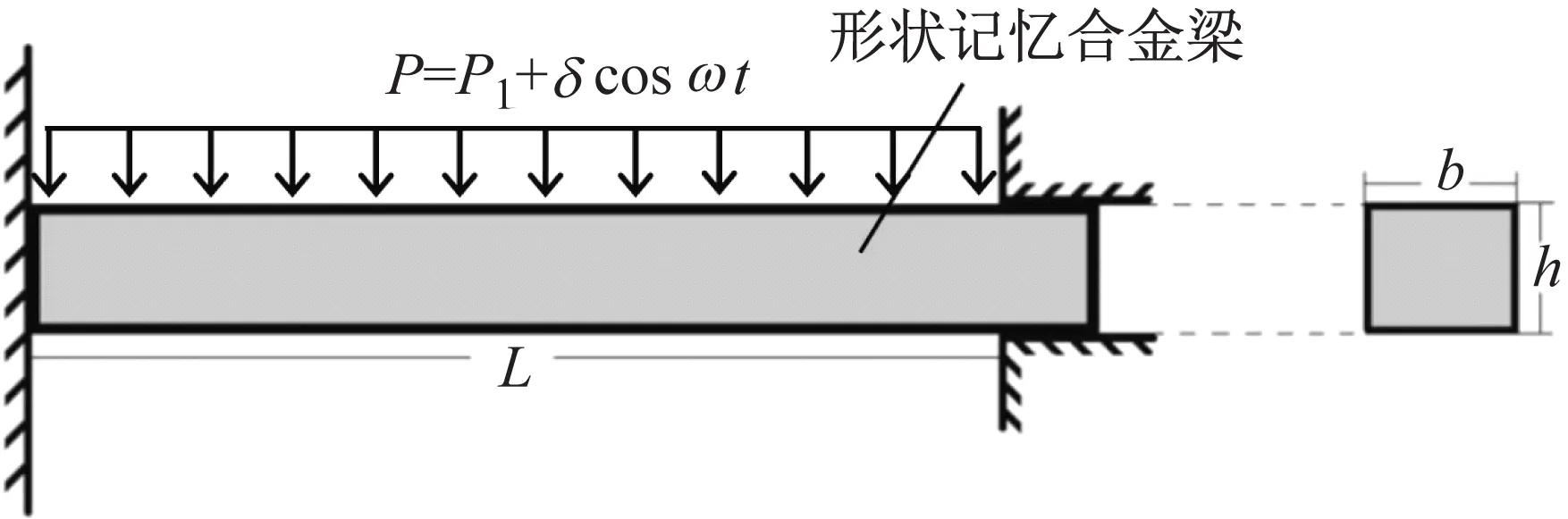
图1 一端固支一端夹支的形状记忆合金梁示意图

由于梁结构材料为形状记忆合金,应力-应变-温度本构模型可以表示为最高次幂为5的多项式,即式(1)中的σ表示为[13]
σ=a1(T-TM)ε-a2ε3+a3ε5
(2)
式中:a1、a2和a3表示形状记忆合金的材料系数;TM表示马氏体相变临界温度[14],当温度低于TM时,合金的马氏体相处于稳定状态;T表示环境温度,假设形状记忆合金梁的导热性很好,则T也可以表示合金梁的即时温度。

结合式(1)和式(2),利用Galerkin法得到形状记忆合金梁横向位移的控制方程

(3)

将式(3)进行无量纲化可得
(4)

式(4)也可以简写为
(5)
其中,G(,θ)=β(θ-1)-γ13+γ25且F(τ)=f1+AcosΩτ。由式(5)可知,改变无量纲温度θ的值会对G(,θ)的线性项带来影响,进而影响整个系统的动力学响应。利用四阶Runge-Kutta法对式(5)进行数值求解,可精确分析形状记忆合金梁的动力学特性。
2 温度对合金梁非线性动力学特性的影响
假设合金梁的材料为Cu-Zn-Al-Ni形状记忆合金,则式(2)中形状记忆合金的各项材料参数取:TM=288 K、a1=523.29 MPa/K、a2=1.868×107MPa且a3=2.186×109MPa。合金梁的几何尺寸取L=300 mm,h=20 mm和b=30 mm。式(5)中横向扰动力F(τ)的无量纲参数设为f1=A=0.5且Ω=1。
考虑与外界无任何形式能量交换的保守系统,系统势能的变化过程可以看作是一个等熵过程,则根据式(5),形状记忆合金梁的势能可以表示为
(6)
结合式(5)和式(6),利用MATLAB数值计算可以得到温度变化条件下的系统平衡点分岔图,如图2(a)所示。其中,粗虚线表示不稳定平衡点集,粗实线表示稳定平衡点集。由图2(a)可知,当θ<1时, 系统处于低温马氏体状态,此时有三个平衡点,包括一个鞍点和两个中心;当θ>1.2时, 系统处于高温奥氏体状态,此时只有一个中心;当1<θ<1.2时, 系统处于相变阶段,因此存在五个平衡点,包括两个鞍点和三个中心。图2(a)表明温度会影响形状记忆合金梁的相变过程,从而影响系统平衡点的个数和振动状态。在图2(a)分析的基础上,图2(b)分别给出了θ=1和θ=1.2时系统的势能曲线(虚线部分),由图可知,随着温度由θ=1逐渐变为θ=1.2,系统的中心势阱(=0)出现并加深,伴随着势阱间阱栅由中心转移到两侧并逐渐增高,而非中心势阱(≠0)弱化直至消失,此时阱栅也一同消失。整个过程中,系统由双势阱系统变为三势阱系统,最终稳定为单势阱系统。根据温度影响下系统势能的转变过程可知,存在一个临界温度θcr,当温度低于该临界值时(θ<θcr),势阱间的阱栅较低,梁在=0的初始位移处获得的机械能可以使其越过阱栅,宏观上表现为低温下系统为双势阱或三势阱时,梁在周期载荷作用下可以产生振幅较大的振动(如图2(b)左图所示);当温度升高(θ=θcr)引起中心势阱加深且阱栅的能垒增高时,梁在=0的初始位移处获得的机械能将不足以使其越过阱栅,于是梁的振幅将明显减小(如图2(b)右图所示)。根据上述理论分析可知,在临界温度θcr附近改变温度,可使合金梁的振动状态发生明显改变,进而影响梁的振幅并实现梁的振动控制。

(a) 平衡点示意图
为了获得临界温度θcr,可以利用最大李雅普诺夫指数[16]来描述梁在温度区间θ∈[1,1.2]内的运动状态,如图3所示。其中,最大李雅普诺夫指数大于零代表系统处于混沌状态,等于零则代表系统处于准周期状态。根据图3可知,当系统温度值θ≤1.163 5,系统的最大李雅普诺夫指数大于零,系统振动处于混沌态且振幅较大;当系统温度为θ>1.163 5,最大李雅普诺夫指数等于零,意味着系统处于准周期运动状态且振幅较小。取θ=1.163 5和θ=1.163 6分别绘制系统的庞加莱截面,如图3右侧所示,观察到θ=1.163 5时,庞加莱截面为离散的点集,表明系统处于混沌态;当θ=1.163 6时,这些点集转变为闭合的环,表示此时合金梁做小振幅的准周期运动。根据上述研究可知,形状记忆合金梁的临界温度约为θcr=1.163 5。

图3 形状记忆合金梁的最大李雅普诺夫指数随温度变化的情况
3 波动温度环境下合金梁的参激振动控制
通过调整温度可以改变形状记忆合金梁的振动特性,其实质是改变了合金梁的刚度,使其在θ≤θcr时表现出柔度较大的软弹簧性质,在θ>θcr时表现出柔度较小的硬弹簧性质。基于此,可以引入波动温度环境作为系统的参数激励,来达到控制形状记忆合金梁非线性振动的目的。
假设环境温度影响下合金梁的温度呈现余弦变化,可以表示为
θ(τ)=θ0±εcosΩθτ
(7)
式中:θ0表示初始温度;ε是温度变化的小扰动参数;Ωθ为温度变化的频率,并且有θ0=θcr=1.163 5,ε=0.01和Ωθ=1。可以看出,温度在临界温度θcr附近波动变化,且波动频率与外激励的频率相同,意味着温度可以即时改变形状记忆合金梁的性质,并放大或减小外激励对梁的作用。
将式(7)代入式(5)中,得到形状记忆合金梁在波动温度场中的振动位移时间响应图,如图4所示,其中图4(a)是温度变化服从θ(τ)=θ0+εcosΩθτ时的振动响应图;图4(b)是温度变化服从θ(τ)=θ0-εcosΩθτ时的振动响应图。由图4(a)可知,当θ(τ)=θ0+εcosΩθτ时,温度的变化规律与外激励完全相同,因而在合金梁振幅达到最大值的时候材料的温度也可以达到最高,从而使合金梁刚度变大,有效减少了梁的振动,其振动振幅比恒温场中(θ(τ)=θ0)梁的振动幅值衰减了约70.41%。若θ(τ)=θ0-εcosΩθτ,如图4(b)所示,环境温度的变化规律刚好与图4(a)的情况相反,即合金梁的振幅最大时,材料温度和刚度反而最低,从而使梁的振动加剧。因此,由图4可知,通过调控合金梁温度场的波动变化规律,可以实现参数激励控制,有效扩大或抑制合金梁的振动,从而灵活应用在实际当中。

(a) 温度变化满足θ(τ)=θ0+εcos Ωθτ
前已述及,围绕临界温度θcr改变温度可以实现合金梁的参激振动控制,因此找到θcr值是非常关键的。由于外激励的形式对形状记忆合金梁的振动有很大的影响,甚至会影响临界温度θcr的值,因此有必要研究不同外激励下系统的临界温度。分别选取外激励的振幅和频率作为变量,利用最大李雅普诺夫指数法,可以通过振幅-温度和频率-温度双参数相图来确定引起系统在混沌态和准周期态之间相互转化的临界温度(亦称为混沌阈值),如图5所示。图5中深色区域对应的最大李雅普诺夫指数等于或小于零,代表系统处于非混沌态,此时合金梁的振动幅值要小;浅色区域对应的最大李雅普诺夫指数大于零,代表系统处于混沌态且梁的振幅较大;混沌态和非混沌态区域间有明显的分界线,临界温度便分布在线上。由图5(a)中的振幅-温度双参数相图可知,当外激励的频率固定为1,随着外激励振幅最大值的增加,系统的临界温度也变得越来越高,这一现象在振幅较小的区间内更为明显。从能量转变的角度看,这种变化趋势的原因是当温度升高时,中心势阱加深,阱栅能垒升高,这个时候系统需要获取更多的动能来越过阱栅实现跨越三个势阱的大振幅运动。此外,由于系统的强非线性,在图5(a)的混沌区域内,同样有小范围的非混沌区域散布其内,且有一定的分形特征。图5(b)给出了系统的频率-温度双参数相图,其中外激励的振幅固定为0.5。从图5(b)中可以发现,系统的非混沌运动更容易发生在低频段和高温区,当外激励的频率相对较大时,混沌运动在变温度场中成为了系统的主要运动形式。图5的结果为不同外激励条件下选取合适的临界温度,进而对系统进行参激控制提供了理论依据。

(a) 当Ω=1时的振幅-温度相图
4 结 论
本文建立了横向周期载荷作用下一端固支一端夹支的形状记忆合金梁振动控制方程,研究了温度影响下合金梁的非线性振动特性,提出了一种利用波动温度场实现参数激励来控制形状记忆合金梁振动的方法。结果表明:温度对形状记忆合金梁的刚度和力学性能有影响,且存在临界温度θcr,当材料温度在该临界温度附近变化时梁的振动状态会发生显著变化(在混沌和非混沌状态之间变化);以临界温度为参考设置波动温度场可以对形状记忆合金梁进行参激振动控制,从而有效抑制和扩大梁的振幅;研究结果还发现,不同外激励对临界温度的影响较大,这为实现合金梁的参激振动控制提供了理论补充。本文提出的方法对形状记忆合金梁或其他结构的振动控制灵活方便,效果显著,具有一定的应用价值。

