基于改进的重复控制永磁同步电机谐波电流抑制方法

黄慈梅，赵小坤，夏铸亮，刘伟，廖展图

广州汽车集团股份有限公司汽车工程研究院，广东广州 511434

0 引言

永磁同步电机因具有体积小、功率密度高、结构简单以及转矩惯性比高等优点，被广泛应用于电动汽车、航空航天等领域。随着电动汽车的迅猛发展，该领域对电机控制系统的性能要求也越来越高。在实际控制系统中，电机输出转矩偏离转矩指令而脉动，转矩脉动的大小是衡量控制系统优劣的重要性能指标，而谐波电流是导致转矩脉动的主要因素。

造成电机谐波电流的主要原因可分为以下两类：①电机本体方面各种能导致电机气隙磁场畸变的因素，如齿槽效应、绕组分布形式、磁路饱和等；②控制系统方面非理想的开关元器件，离散的控制系统等引起的谐波电流。

对于抑制谐波电流，国内外专家学者做了大量的研究工作，并提出了各种方法。比如，在电机本体方面，采取优化电机本体设计的措施，使空载气隙磁密靠向理想的正弦分布。在逆变器方面，采取死区补偿和电流过零点补偿等措施对谐波电流进行抑制，这些方法也有一定的效果。随着谐波电流抑制研究工作的不断深入，更多的方法被提出，如谐波注入法、PI迭代学习、增加重复控制器等。

重复控制可以对电机电流频率的整数倍电流谐波进行抑制。通过抑制谐波电流，从而改善转矩脉动。然而，传统的重复控制算法复杂，且需占用大量的存储空间。文献[16]提出了一种改进的重复控制算法，在特定频率上采用了傅里叶分析和信号重构的方法，能大大简化算法，同时避免了使用多余的存储空间，其试验结果表明，此方法可以很好地抑制电流高次谐波。然而，随着电机运行频率的升高，此方法的作用被限制。

文中对以往的重复控制方法进行改进，采用傅里叶分析法提取某一特定次的电流谐波信号，对其进行滤波与积分，然后与补偿后的角度信号一起进行信号重构，通过系数修正与限幅后，产生、轴电压的补偿分量，叠加在原先由PI调节器产生的、轴电压给定值上，共同作用于永磁同步电机，实现谐波电流抑制。为了验证该方法的有效性，搭建了45 kW永磁同步电机控制系统并进行了有关试验。试验结果表明，此方法在较高电流频率内都能有效地抑制、轴的电流脉动，相比传统的重复控制，扩大了适用范围。

1 PMSM控制模型

1.1 永磁同步电机数学模型

永磁同步电机的数学模型如下：

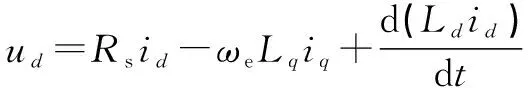
(1)

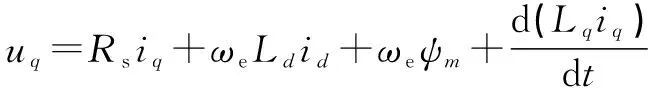
(2)

式中：、为、轴电压；、为、轴电流；、为、轴电感；为电机的电角速度。

实际的永磁同步电机是非理想的，其、轴电感会随着负载电流的大小而变化，且永磁磁链也会因为温度的升高而出现一定的退磁现象。除此之外，在采用斜槽的电机中，齿槽效应会引起永磁磁链和、轴电感随电机转子位置变化。

1.2 永磁同步电机矢量控制系统框图

永磁同步电机矢量控制的基本思想是通过坐标变换，将静止坐标系中定子电流空间矢量分解为、旋转坐标系中的两个分量：励磁电流分量和与之垂直的转矩电流分量，通过调节和的大小，即可获得指定的转矩输出。矢量控制以转子磁场定向，控制简单、系统动态性能好、控制精度高、运行平稳、转矩脉动小。

文中所采用的永磁同步电机矢量控制系统框图如图1所示。

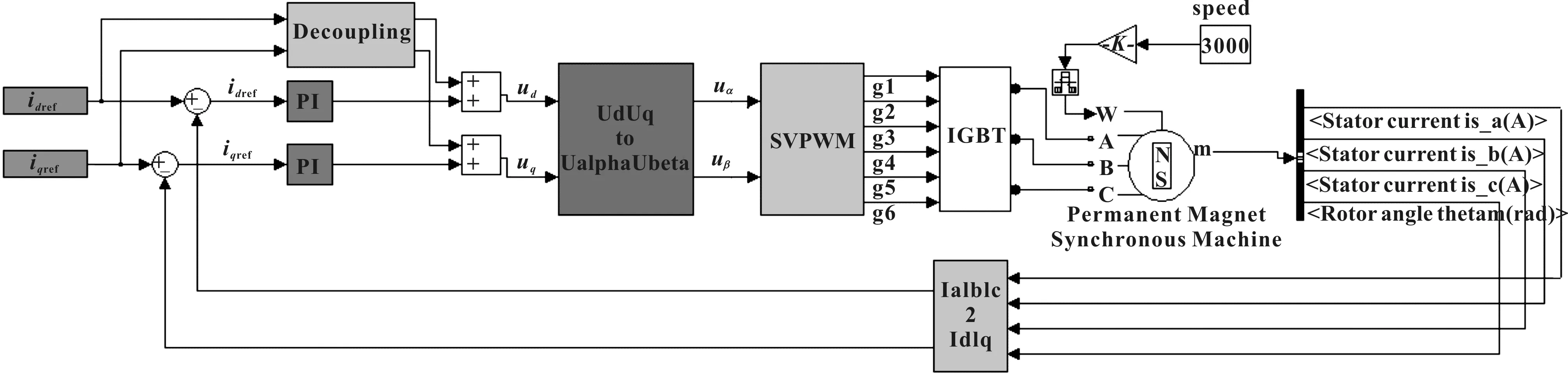
图1 永磁同步电机矢量控制系统框图

图中，ref、ref分别为轴电流给定值和轴电流给定值;、分别为轴电压给定值和轴电压给定值。

试验时，采取直接给定ref、ref进行控制的方式。电机实际三相电流通过传感器采样，进行坐标变换后转化为、，对其进行频谱分析即可得知谐波电流大小和频率。

2 重复控制

2.1 传统的重复控制

重复控制利用延时环节和正反馈组成，一般将重复控制器与传统的PI调节器并联，其结构如图2所示。

图2 重复控制器与PI调节器并联结构

其中Decoupling为、电压的解耦环节。在不考虑谐波电流抑制时，、由电压解耦环节和PI环节生成。为了抑制谐波电流，增加与PI环节并联的重复控制环节。如图2所示，传统重复控制中需要个延时环节，重复控制频率为=1，其中为数字控制周期，个单位延时环节就需要个存储空间。在重复控制频率以及其整数倍处的扰动可以通过图2所示的控制结构进行抑制，在这些频率点，扰动增益为零。这些是重复控制器的基本特性。

但在这些频率点附近出现的一些尖峰会影响整个系统的性能。一般地，为了使系统更加稳定，通常会在重复控制器前串联高通滤波器，并且在其后串联低通滤波来优化整个频域的性能,从而导致传统重复控制器的设计非常复杂。

而且，在变频系统中，谐波的频率与基频成正比并随其变化，为了对变频的谐波进行控制，就需要调整存储空间，使得=1(·)。当重复控制频率极低时，需要很大的存储空间。

2.2 改进的重复控制

采用改进的重复控制后，同样是重复控制结构与PI调节器并联，作用于永磁同步电机的电流控制。不过，相比传统的重复控制，改进的重复控制内部结构发生变化，针对特定次数的谐波电流，采用傅里叶分析，并创新地用补偿后的角度进行信号重构，再经过一个比例环节和限幅环节，最终生成补偿电压，与PI调节器产生的电压相加。改进的重复控制结构如图3所示。图中，err是轴参考电流ref和需要被改善的轴实际电流的差值，是重复控制器的输入信号，其中包含了频率的电流谐波，_out是改进的重复控制的输出信号，将其与PI控制产生的电压相加，即生成轴电压参考信号ref。同样，对于轴电流的改善，也是与轴电流相同的流程。改进的重复控制器与PI控制并联结构如图4所示。

图3 改进的重复控制结构

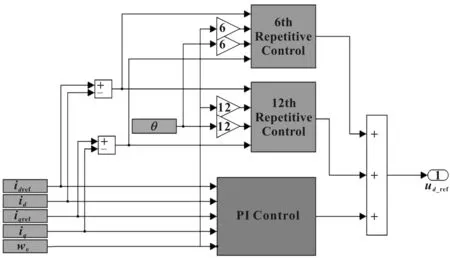
图4 改进的重复控制器与PI控制并联结构

图3中的傅里叶分析模块负责err中频率为的信号幅值的提取，相当于一个单一频率的滤波器，只接收频率为的信号输入。图中傅里叶分析的输出、由式(3)确定：

(3)

式中，令=(2π)，则=1(·)。将上一次的估算值进行滤波后，与此次更新的、进行叠加。、的更新周期为·，这就决定了其延时累加的特性与传统的重复控制器相同。在信号重构时，利用补偿后的角度的余弦值cos和正弦值sin来参与信号的重构，这一点在重复控制频率较高时尤为重要。重构后的信号经过比例环节和限幅环节，即可输出最终的_out。

改进的重复控制只是对单一频率的重复控制，因此，如果需要对多个频率的信号进行重复控制，就需要多个如图3所示的模块进行叠加，共同作用于控制系统。如图4所示，为了抑制、电流中的6次和12次谐波，就采用了两个模块进行叠加。

理论上，=1(·)，但在离散系统中，取的是一个相近的整数值。这样，在Fourier分析时就会产生误差，当值比较大时，这一误差并不影响重复控制的效果。但是当重复控制频率很高时，值很小，如当<10时，就需要采取补偿后的角度来进行信号重构。当然，值也有下限值，按照试验结果，值不能小于3，否则会引起重复控制的失效并恶化原有信号。

3 试验结果

为了验证上述改进的重复控制算法，在试验室搭建了一个永磁同步电机的实验平台。所使用的永磁同步电机的参数见表1。

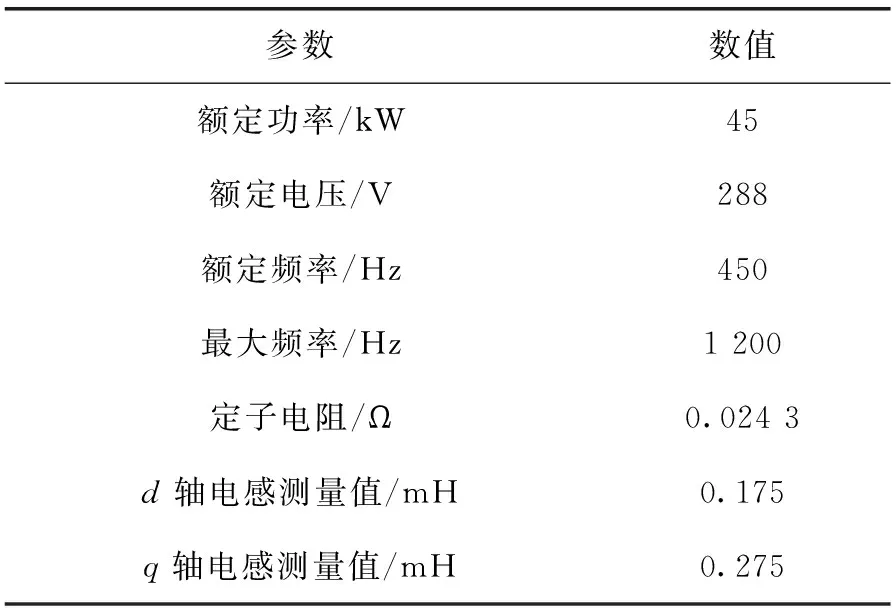
表1 永磁同步电机参数

在试验中，当永磁同步电机运行在2 000 r/min下，ref=-10 A，ref=123 A时，分别对不加改进重复控制的软件和采用改进重复控制后的软件进行试验，使用Lauterbach采集由实际三相电流、、经Park变换后的实际轴电流、轴电流。对两次实验中采集的实际轴电流、轴电流进行频谱分析。

对不采用改进重复控制的软件进行试验后，经电流频谱分析发现，轴电流的脉动谐波主要为1、3、6次谐波，其他次谐波电流较小；轴电流的脉动谐波主要为6次谐波，其他谐波电流较小。

针对此情况，对轴电流进行1、3、6次谐波的改进重复控制、对轴电流进行6次谐波的改进重复控制。然后对采用改进重复控制后的软件进行试验。

两次试验的结果分析如图5至图10所示。

图5 未采用改进重复控制的id电流波形

图6 采用1、3、6次改进重复控制后的id电流波形

图7 频谱分析对比

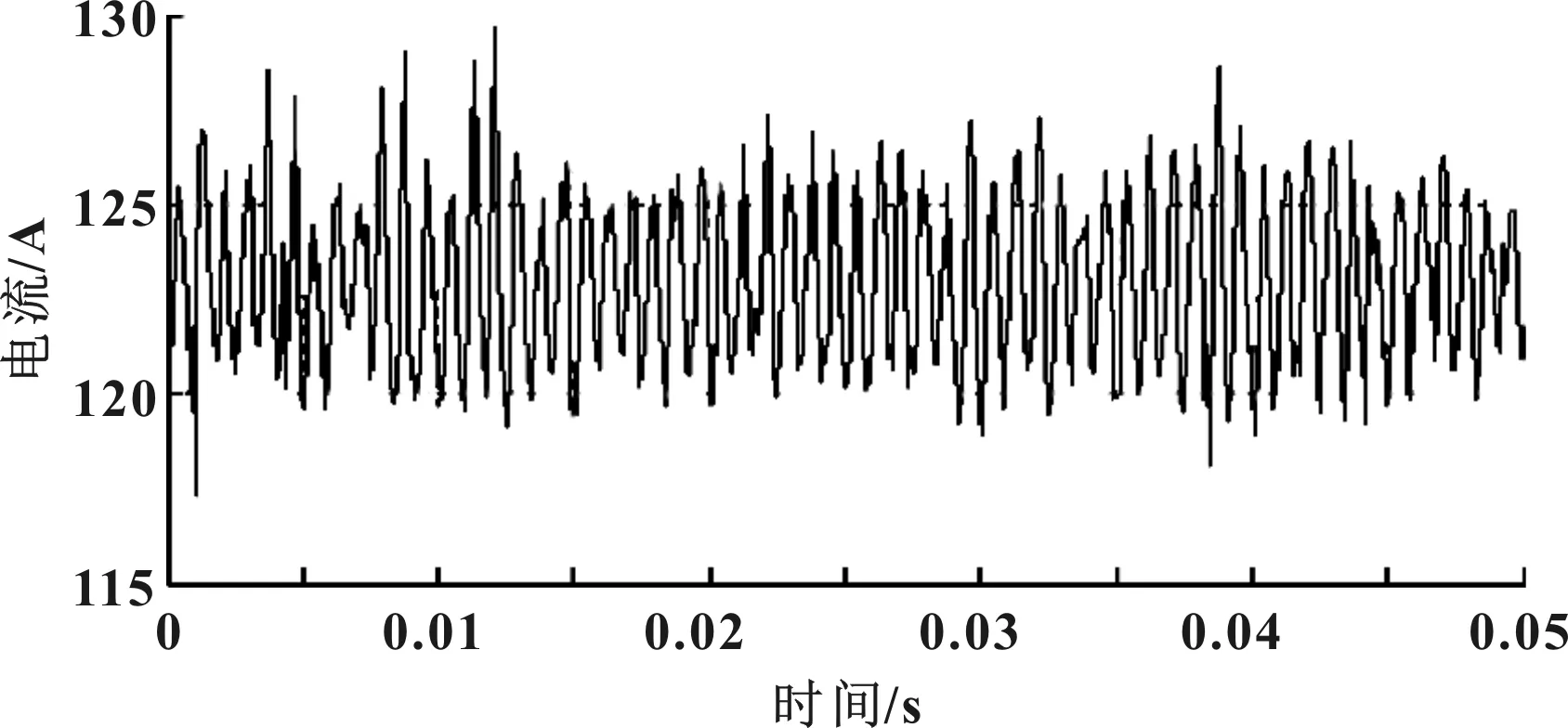
图8 未采用改进重复控制的iq电流波形

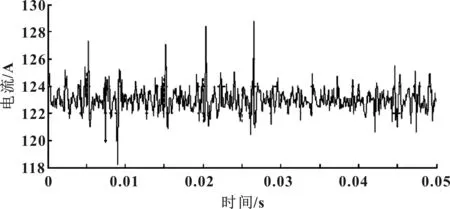
图9 采用6次改进重复控制后的iq电流波形

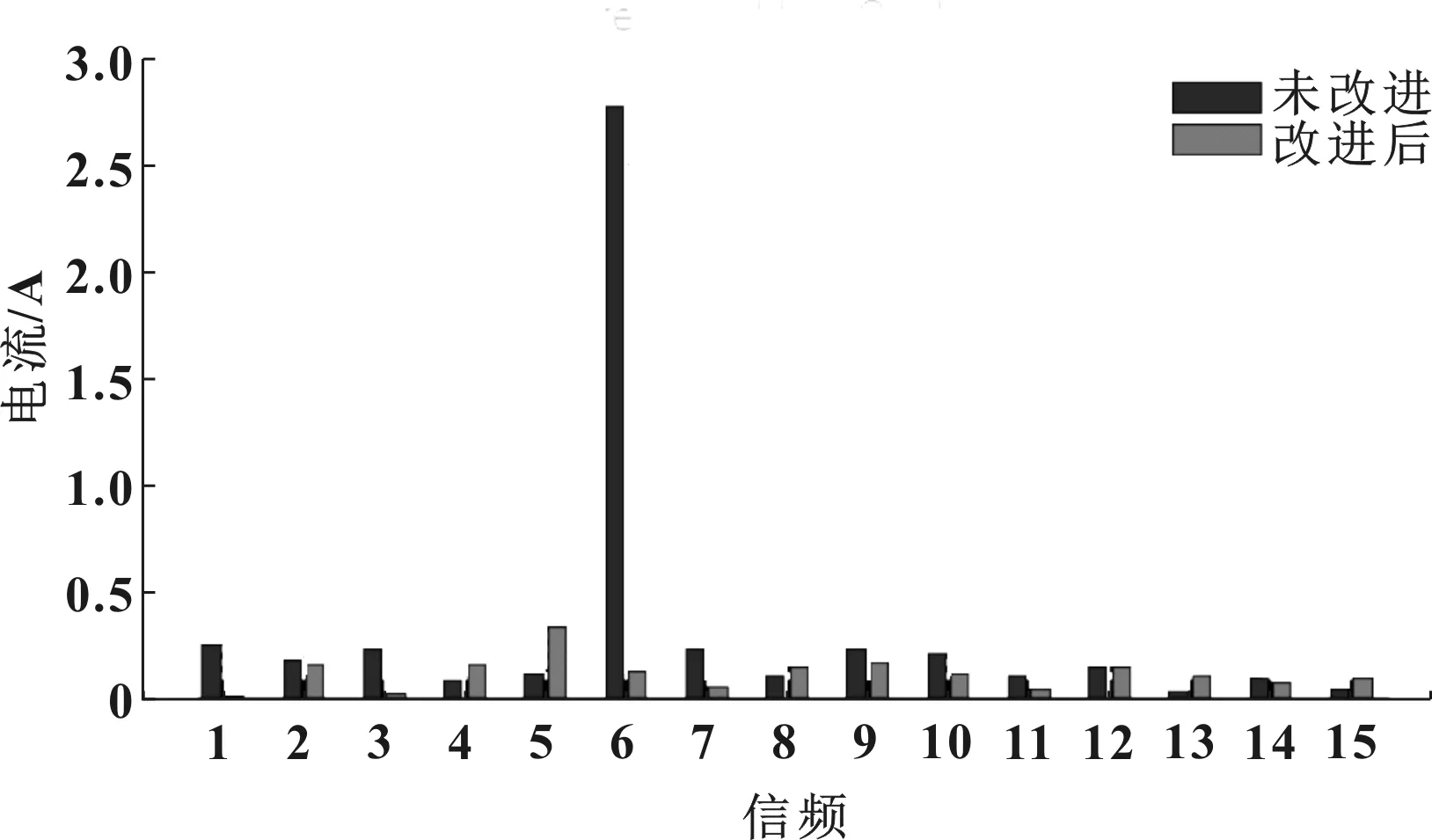
图10 频谱分析对比

由试验结果可知，对于轴电流，重复控制前后，1次谐波的幅值由3.5 A下降至小于0.2 A，3次谐波的幅值由1.3 A下降至小于0.1 A，6次谐波的幅值由3.5 A下降至小于0.2 A;对于轴电流，重复控制前后，6次谐波的幅值由2.7 A下降至小于0.2 A。由此可见，改进的重复控制可以将谐波电流抑制90%以上。

4 结束语

该方法通过利用傅里叶分析对指定次数的谐波电流进行提取、信号重构与角度补偿而产生、轴电压的补偿分量，叠加在原有、轴电压给定值上，共同作用于永磁同步电机，实现谐波电流抑制。将该方法应用于45 kW的永磁同步电机控制系统进行验证，试验结果表明，该方法在较高电流频率内都能有效地抑制、轴的电流脉动，相比传统的重复控制，扩大了适用范围。