2-尺度三维八向双正交小波包及其性质

张静，卢维娜，刘芳园

（新疆师范大学 数学科学学院，新疆 乌鲁木齐 830054）

小波包由Coifman 与Meyer［1-2］初始研究并引入，因其能够对信号进行分解处理，在语言、图形和地震等方面得到广泛应用［3-6］；例如，利用小波包变换去噪，处理机械振动、地震波等工程信号问题［7-10］。此外，为弥补小波包在信号处理中的不足，Daubechies 和Cohen 等开始致力于双正交小波包的研究［11-14］。2007年，双向小波的概念被提出［15-16］。近年来，国内外学者对高维度上正交小波包问题进行了研究［17-18］，如Shah FA，Bhat MY 研究了特征局部场上双正交小波包的构造［19］等。尺度为小波函数的伸缩状态，在信号处理过程中应用大尺度小波变换处理信号往往可反映出信号整体的近似特征，而运用小尺度小波变换处理信号可获得信号细节信息，一般情况下研究2-尺度小波函数及相关性质居多。文章在a-尺度三维八向加细小波尺度函数的构造算法［20］与双正交的a-尺度三维八向尺度函数和小波函数构造算法［21］研究的基础上，给出了2-尺度三维八向双正交小波包的定义，并对其做Fourier变换得到其相应的8×8的对称矩阵Γ，最后探究了2-尺度三维八向小波包的双正交性，这是研究成果［20-21］在伸缩尺度为2状态下的扩展研究。

1 2-尺度三维八向双正交小波包的定义

为定义2-尺度三维八向双正交小波包，根据已有研究成果［20-21］，先规定如下记号：

1.1 2-尺度三维八向小波函数族

其对应的双正交小波函数族如下：

1.2 选择2-尺度三维八向小波合适的序列（即：面具符号）

则相应的双正交小波合适序列（即：面具符号）为：

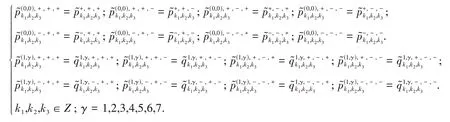
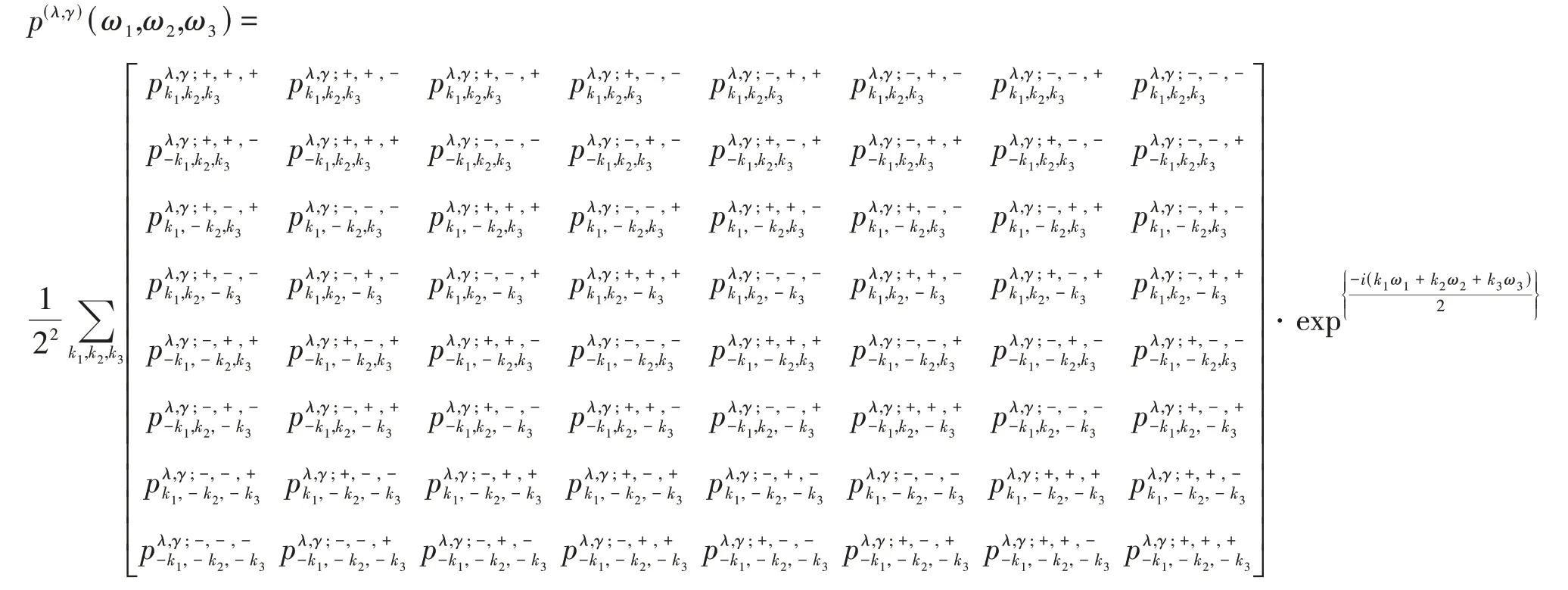
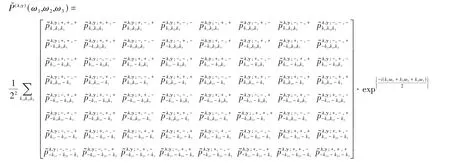
其中：λ = 0,1; γ = 0,1,2,3,4,5,6,7.

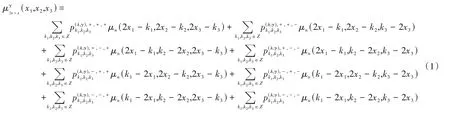
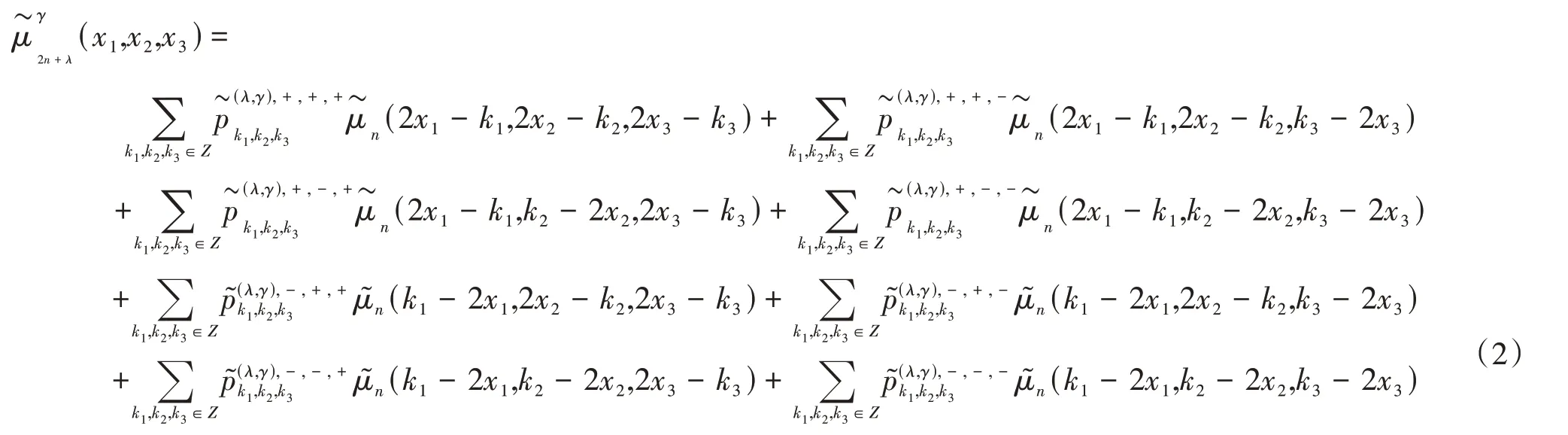
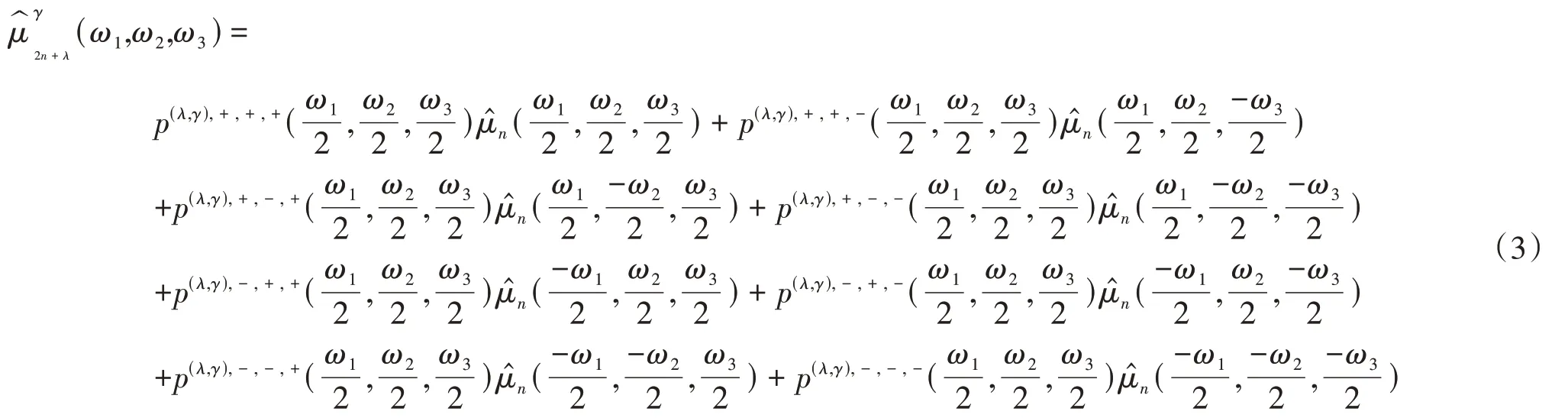
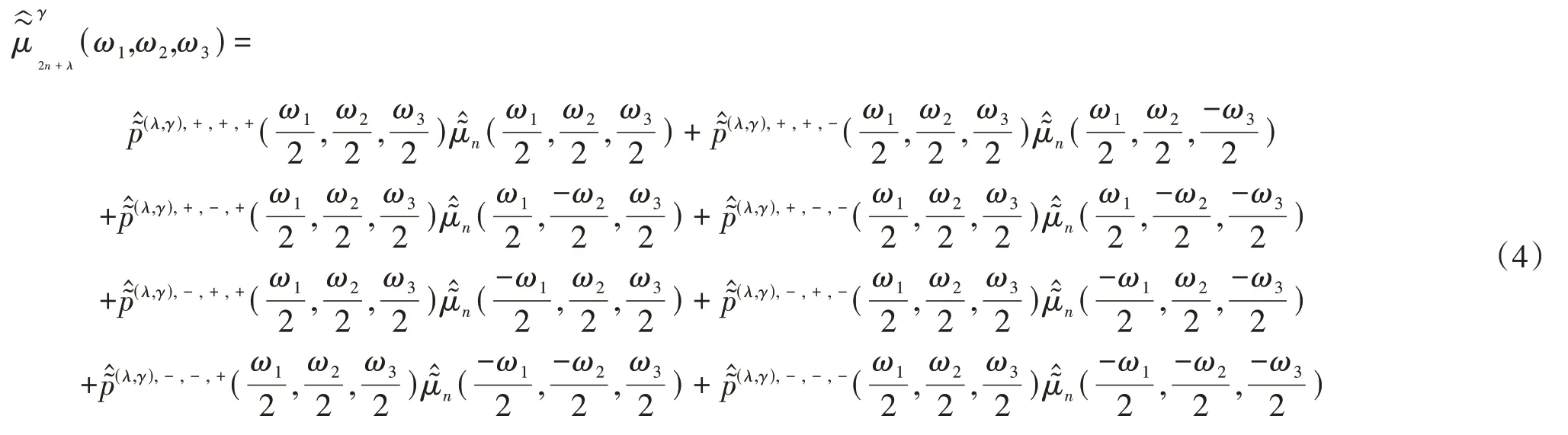
为了对2-尺度三维八向双正交小波包做进一步研究，于是令：

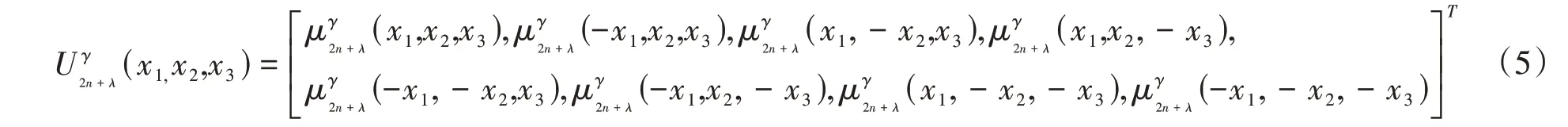
于是存在对称矩阵：

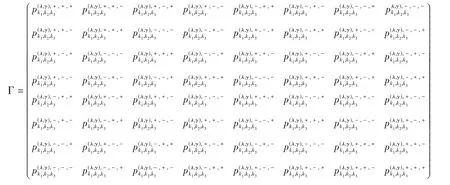
则可得：

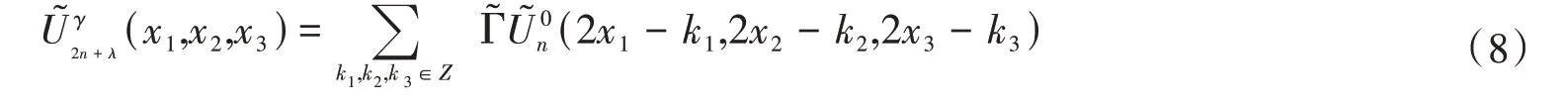
其加细面具符号如下：

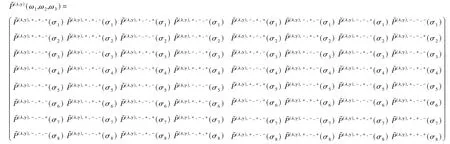
其中：λ = 0,1; γ = 0,1,2,3,4,5,6,7.

由以上变换，可得：

其中：j,h = 0,1; s,m = 0,1,2,3,4,5,6,7.式（9）相当于

其中λ = 0，1; γ = 0,1,2,3,4,5,6,7; n1,n2,n3∈Z.

2 2-尺度三维八向双正交小波包的性质

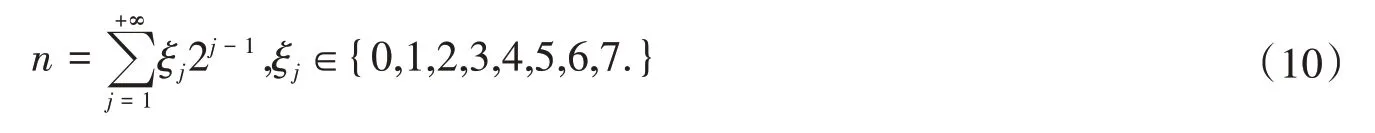
得到一个有限和，且此展开式是唯一的。

证明 如果2S0-1≤n ≤2S0，根据带余除法，有n = 2S0+ n1(0 ≤n1≤2S0-1)，之后再利用带余除法把n1展开，并不断重复此过程则可得到，其中于是引理得证。

构造的2-尺度三维八向双正交小波包，则当，存在：

证明 （1）当n= 0时，上式显然成立；（2）当0 ≤n ≤2S0（S0是某个正常数）时，（11）式成立；当且仅当2S0≤n ≤2S0+1时，根据引理2.1，有：2S0-1≤（[ x ]表示不超过x的最大整数），.时，通过数学归纳法即可证明结论。

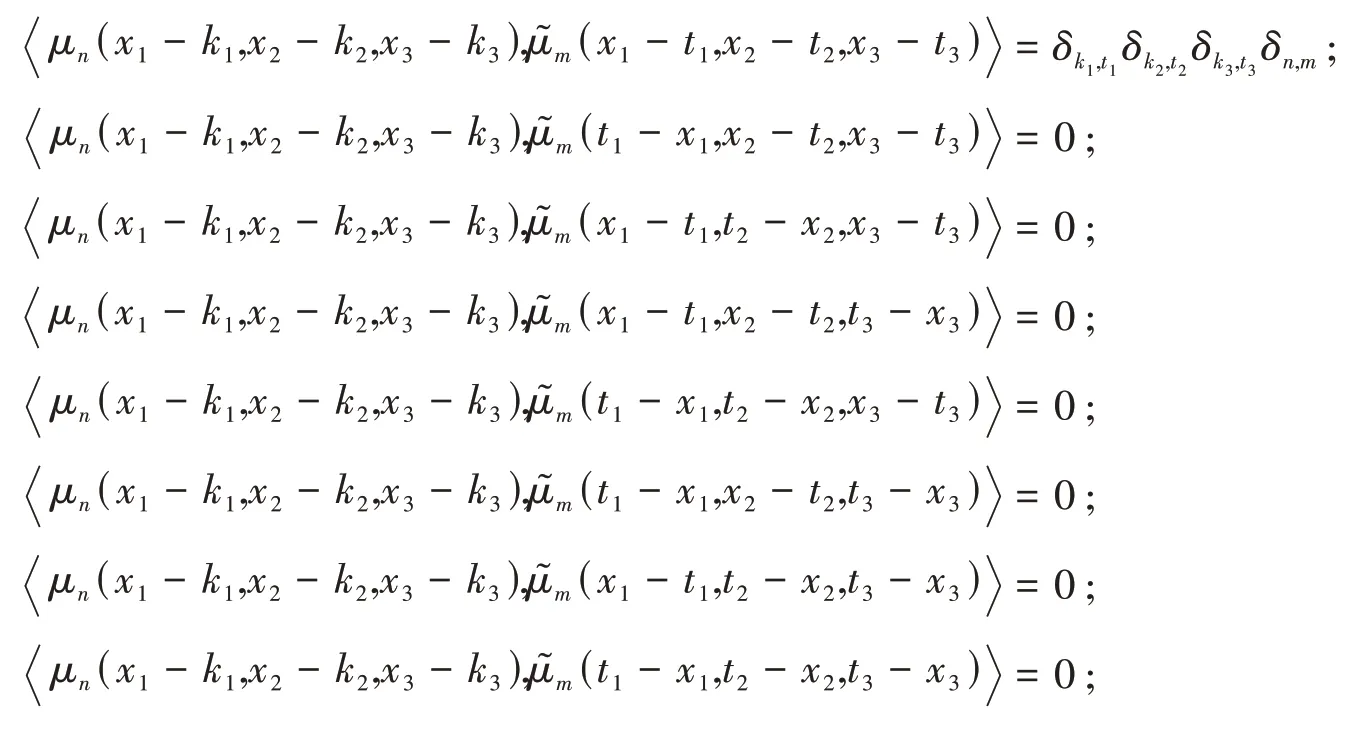
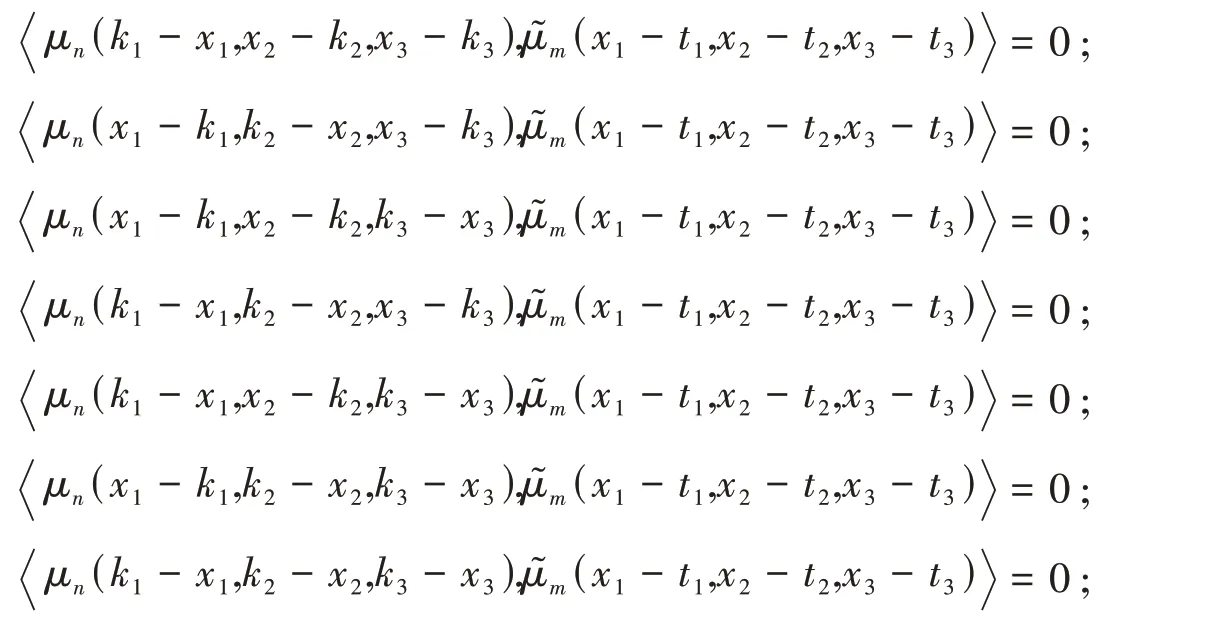
其中k1,k2,k3,t1,t2,t3∈Z; n,m ∈N.

证明 因尺度函数φ(x1,x2,x3)与φ͂(x1,x2,x3)的双正交性（文献［21］定理2.1），以及ψ1,γ(x1,x2,x3),与，γ = 1,2,3,4,5,6,7.的双正交性（见文献［21］定理2.2），则有：

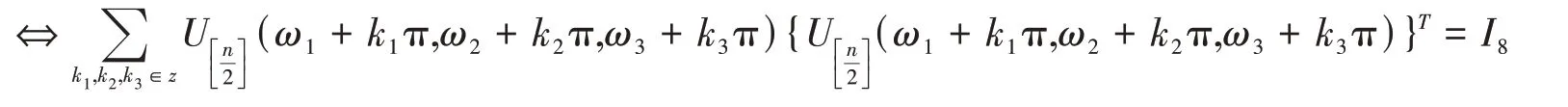
因而有：

其中：λ = 0,1; γ = 0,1,2,3,4,5,6,7.于是结论得证。

定理2.3 若函数族} = 0，1; γ = 0,1,2,3,4,5,6,7. 与 = 0,1；}γ = 0,1,2,3,4,5,6,7. 为双正交小波函数，γ = 0,1,2,3,4,5,6,7.（见文献［21］定理2.2）的2-尺度三维八向双正交小波包，则有：

证明 证明上述结论成立等价于证明下列式子成立：

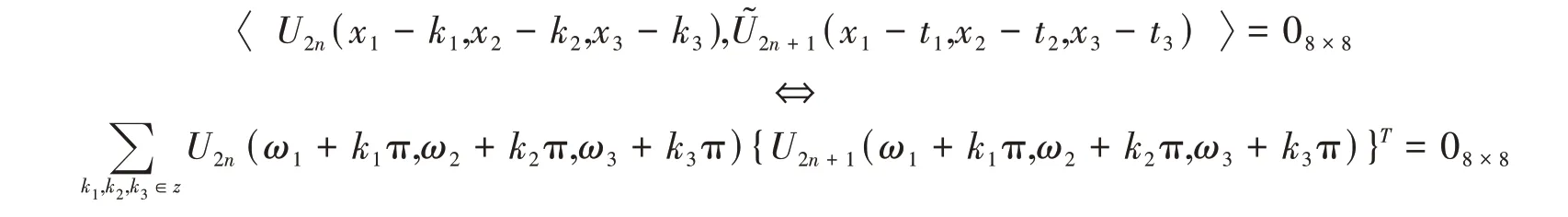
根据文献［21］定理2.1式（12）与定理2.2式（13），于是有：

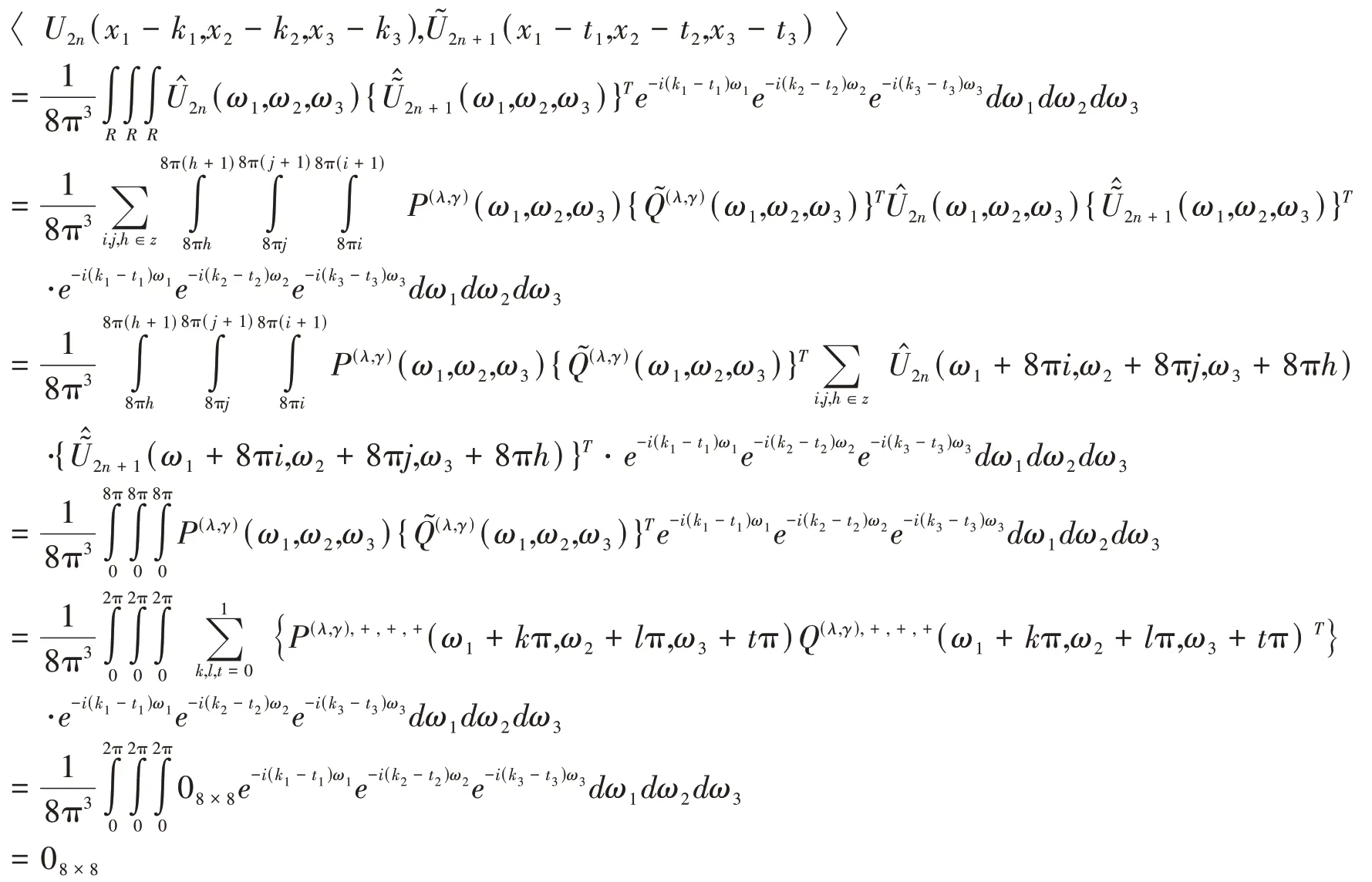
其中：λ = 0,1; γ = 0,1,2,3,4,5,6,7.于是结论得证。

3 结论

依据双向小波理论，在a-尺度三维八向尺度函数和小波函数算法分析研究的基础上，给出了2-尺度三维八向双正交小波包的定义，并对其做Fourier变换得到8 × 8的对称矩阵Γ，最后探究了2-尺度三维八向双正交小波包的双正交性质。通过探究将一维双正交双向小波包的相关结论推广到2-尺度三维八向双正交小波包，为小波包在信息领域的进一步运用提供了高维小波的分析依据。