面向共同CM时具搭便车行为OEM的流程投资策略
夏 晶, 牛文举, 沈厚才
(1.南京大学管理科学与工程系,江苏南京 210093;2.南京财经大学营销与物流管理学院,江苏南京 210023)
1 引 言
随着行业竞争的加剧, 越来越多的原始设备制造商(original equipment manufacturer, OEM)把产品生产、制造和组装等业务以合同订购的方式外包给合约制造商(contract manufacturer,CM),自己仅专注于产品的设计、研发和销售渠道的控制,从而实现降本增效[1−3].但生产外包下,OEM无法直接控制CM的生产流程,产品生产成本可能处于居高不下的状态.为此,OEM 有意愿对CM进行先进设备投资、技术协助、员工培训等形式的流程投资,以降低产品生产成本、增强成本竞争优势[4,5].
然而,实际中普遍的现象是,一个CM会与多个竞争OEM保持合作关系.当一个OEM对共同CM进行流程投资时,它有可能面临搭便车问题:流程投资在改善自己的产品生产成本的同时,也会在CM处因生产设备、制造工艺、组装流水线等资源的部分甚至完全共享而降低对手的产品生产成本[6].工业实践中,不同的企业对搭便车现象持有的态度迥异,它们的流程投资策略选择也不尽相同.例如,苹果和高通专注于手机芯片的设计和研发等前端业务,把中端制造和末端封装业务外包给了台积电等企业.但两家芯片竞争企业都无惧搭便车现象,对台积电投资10多亿美元来改善芯片生产工艺、降低生产成本1https://www.fudzilla.com/28545-tsmc-tells-apple-and-qualcomm-where-to-stick-their-money.广东裕元集团作为全球鞋业代工巨头,品牌客户包括Adidas、Nike和New Balance等.尽管鞋类的裁剪、车缝和成型等生产流程存在着资源共享,Adidas仍然对裕元集团进行了诸如员工培训、建设信息系统等形式的流程投资提高其产品生产效率,其他企业尚未做出类似举动2https://www.adidas-group.com/en/sustainability/compliance/supply-chain-approach.由此可见,即使意识到搭便车现象的客观存在性,不同的OEM在对共同CM的流程投资策略选择上却呈现出了差异性.本文试图研究如下问题,揭示该现象背后可能的原因:流程投资存在搭便车时,竞争OEM是否应对共同CM 进行投资降低产品生产成本? 采取和不采取流程投资策略的边界条件是什么? 搭便车行为、市场竞争等如何影响OEM 的流程投资策略选择?
流程投资包括但不限于专业技术、先进设备和人力资源等形式的投资, 目的在于降低企业的生产成本、提高生产效率,它对企业增强成本竞争优势具有重要的影响[7−9].目前,学者们已从多种视角对流程投资问题展开了研究.例如,双寡头的投资效率问题[10]、多周期博弈下的投资决策[11,12]、不同渠道结构下的投资决策[13],以及生产外包对竞争环境下流程投资的影响[14]等.但上述文献并没有考虑企业间的流程投资搭便车行为,而且均假设企业会付出流程投资来改善生产成本,缺乏对竞争环境下流程投资策略选择条件的刻画与分析.作为经济社会中一种普遍存在的现象,搭便车问题最初在经济学领域得到关注,随后,逐渐扩展到供应链管理、运营管理甚至金融学等领域,当前已有丰硕的研究成果.从经济学的角度来看,搭便车与正向外部性、溢出效应等概念同义,是指企业或者个人向市场之外所施加的影响并使他方无需付出成本即可获益[15−17].现有文献中,以D’Aspremont和Jacquemin的研究[18]最具代表性,他们讨论了双寡头互相搭对方研发投资便车时的投资决策问题,成为了经典的“AJ模型”.Levin等[19]实证了研发投资搭便车现象并指出,在一定条件下,搭便车行为可以促使竞争企业提高研发投资水平.Harhoff[20]从理论分析的角度拓展了Levin等[19]的研究,得到了搭便车行为能提高企业的创新水平等结论.随后,大批学者从不同视角拓展了“AJ模型”,如搭便车行为对竞争供应链技术创新的影响[21]、多寡头搭便车时的投资策略[22−26].Gupta[27]在文献[13]的基础上,分析了流程投资搭便车对渠道结构的影响,发现较高程度的搭便车更有可能使渠道呈现分散式结构.Ge[7]的研究表明,企业采取非合作研发时,较高程度的搭便车会给它们带来更多的收益;若企业采取合作研发,该结论仅在某些条件下成立.Chen等[28]研究了由一个CM和一个OEM组成的供应链中,前者可以通过搭后者的技术便车降低产品生产成本.结果表明,技术搭便车提高了OEM的生产外包积极性.Veldman和Gaalman[29]探讨了双寡头互相搭对方流程投资便车时,最优流程投资水平设定的问题.Wang[6]研究了具搭便车行为的供应链中,两个竞争制造商是否应对共同供应商进行投资提高供货可靠性的问题.得到的主要结论是,尽管制造商的最优投资水平会因搭便车系数的增大而下降,但它们的期望收益还是会得到改善,互相搭便车的制造商愿意对共同供应商进行投资.L´opez和Vives[30]考虑了所有权存在重叠的多个企业为降低生产成本而进行研发投资,但投资存在搭便车时的问题.结果表明,当搭便车程度处于较高或中等水平时,企业的所有权重叠度越高,它们的研发投入越多.Capuano和Grassi[31]研究了搭便车行为对企业合作研发的影响并指出,搭便车效应越强,企业的合作研发动机越大.李昌文等[32]的研究表明,若搭便车系数较小,两个企业组成的研发合作联盟结构稳定,否则,只有大联盟结构稳定.最近,Li和Bosworth[33]实证了研发投资搭便车对供应链企业的生产效率的影响,发现它能够激发企业的研发投入.
通过文献梳理可知,学者们研究了多种不同情形下的流程投资决策问题,探讨了流程投资搭便车对企业决策和收益的影响,得到了许多有价值的研究结论.如今,企业独自包揽产品设计、生产、制造和销售等全流程业务已不太现实,行业竞争格局的变化、经济的全球化均迫使它们将生产和制造等业务外包.在这一背景下,企业的流程投资存在着更为复杂的、不受控的搭便车问题.然而,上述文献着重考虑了企业间流程投资的横向搭便车.为完善现有研究,本文聚焦于竞争OEM的流程投资在上游共同CM处存在搭便车时的问题.尤其需要指出的是,现有文献大多给定企业采取流程投资策略,然后关注不同环境下的流程投资水平确定和搭便车行为的影响分析,却忽略了一个核心问题:竞争企业在什么条件下才有动机对共同CM进行流程投资?显然,唯有确定了企业愿意采取流程投资策略的条件,才能进一步回答最优投资水平是多少、搭便车行为的影响有多大等问题.本文拓展流程投资搭便车方面的研究,找出了竞争OEM对共同CM进行流程投资的边界条件,揭示了搭便车系数等对最优流程投资策略的影响,较完整地回答了上述问题.
本文研究两个竞争OEM能够在共同CM处搭对方流程投资的便车时,它们的最优投资策略问题.采用博弈论的方法构建不同情形下的模型,讨论搭便车系数、产品替代程度和初始生产成本之差等对企业最优决策和收益的影响.在此基础上,给出管理启示,为搭便车环境下竞争企业的流程投资提供理论决策参考.
2 具搭便车行为OEM的流程投资模型
2.1 符号与假设
考虑两个竞争OEM(记为1和2)把产品生产、制造和组装外包给一个共同CM(记为m),它们仅负责各自的产品定价和销售.根据文献[3,5],逆需求函数表示为

其中a表示市场潜在需求规模;pi为OEMi的零售价格;qi和qj分别代表OEMi和j的产品需求,q= (q1,q2);b ∈(0,1]为产品替代程度,b越大,表示产品替代程度越高,两个OEM的产品竞争越激烈.
CM为OEM 1和OEM2生产单位产品付出的成本分别为c1=c和c2=c+ζ,其中c代表无流程投资时的初始生产成本,参数ζ代表两种产品的初始生产成本之差.ζ >0意味着OEM 1 相对于OEM 2 拥有产品初始生产成本优势.产品初始生产成本可由OEM对CM进行流程投资得以改善,包括但不限于先进设备投资、技术协助和员工培训.两种产品在生产的过程中,会在CM处共享生产设备、制造工艺、组装流水线等资源.因此,一个OEM的流程投资在降低自身产品生产成本的同时,也可能降低对手的产品生产成本,即OEM 之间存在流程投资搭便车行为.根据文献[5,7,18], 两个OEM都对CM 进行流程投资后, 每个OEM改善后的产品生产成本为˜ci(x) =ci −(xi+ηxj),其中xi和xj分别表示OEMi和j付出的流程投资水平,x= (x1,x2);0 ≤η≤1 为搭便车系数,它刻画了OEMj的流程投资能够在多大程度上改善OEMi的产品生产成本.η越大,说明搭便车越严重,每个OEM从对手的流程投资中获得的产品生产成本改善越显著.实际中,搭便车系数的大小取决于CM对生产资源的利用和配置状况: 两种产品完全共享生产资源时,η=1;不共享任何资源时,η= 0;部分阶段共享生产资源,其余阶段采用定制化生产资源时,0< η <1.不失一般性,每个OEM承担的流程投资成本记为fi+φi其中fi,φi >0 分别代表固定投资成本和投资成本系数,φi越大,OEMi的流程投资效率越低.综上,每个OEM 采取和不采取流程投资策略时的收益函数分别为
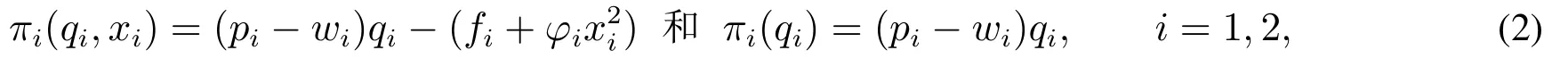
其中wi,wj分别表示CM为OEMi和j设定的单位批发价格,记w=(w1,w2).
在有无流程投资下,CM的收益函数可分别表示为
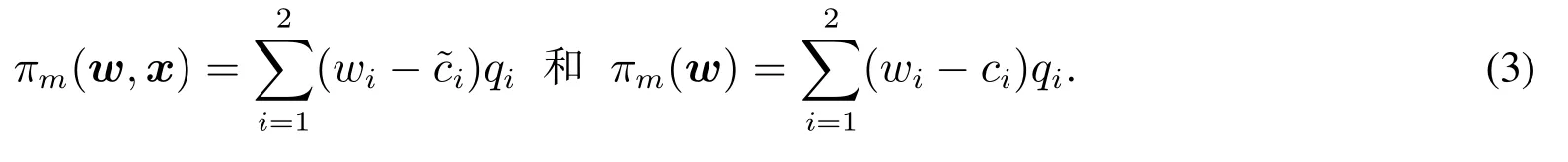
企业的所有决策为公共信息, 并假设流程投资决策先于其他决策, 原因在于生产效率的改进是不易实现的长期过程, 不如产量和价格等决策变化的频繁、迅速.具体博弈时序如图1所示并表述如下: (i) 两个OEM同时非合作决定是否对共同CM进行流程投资;(ii)选择投资的OEM确定流程投资水平;(iii)CM为两个OEM设定产品批发价格;(iv)两个OEM确定各自的产品订购量;(v)基于市场出清价格,需求实现.
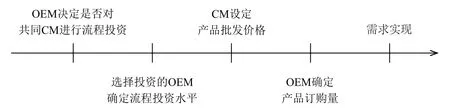
图1 博弈时序Fig.1 Game sequence
下面,构建四种情形下的决策模型: 两个OEM都采取流程投资策略(情形II)、单一OEM采取流程投资策略(情形IN或者情形NI),以及它们都不采取流程投资策略(情形NN).
2.2 OEM都采取流程投资策略(情形II)
当两个OEM都采取流程投资策略时,各方既是投资方又是搭便车者.每个OEM改善后的产品生产成本为=ci −(xi+ηxj),目标是确定订购量最大化式(2)中的收益函数πi(qi,xi).求解得到OEMi的关于批发价格的最优订购量
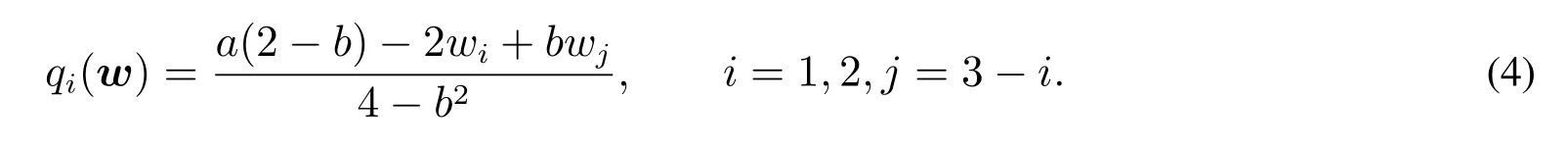

命题1不同情形下的模型均衡结果如表1所示.
2.3 单一OEM采取流程投资策略(情形IN/NI)
首先,考虑OEM 1为唯一投资方的情形,并记为“IN”.此时,OEM 1和OEM2改善后的产品生产成本分别为=c1−x1,=c2−ηx1.OEM 1和OEM2确定订购量最大化各自的收益,即
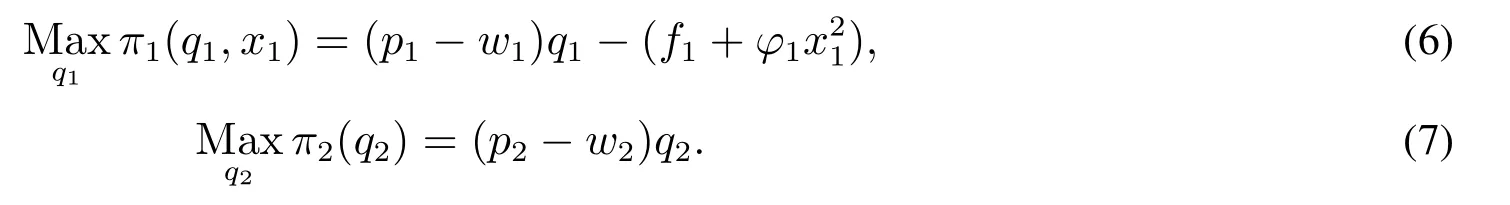
求解得到最优订购量qi(w),如式(4)所示.CM收到最优订单后,为两个OEM设定批发价格最大化个体收益,表示为Maxw πm(w)=(w1−c1+x1)q1(w)+(w2−c2+ηx1)q2(w).求解该问题并将最优批发价格代入式(4),OEM 1在流程投资阶段的收益最大化问题可改写为
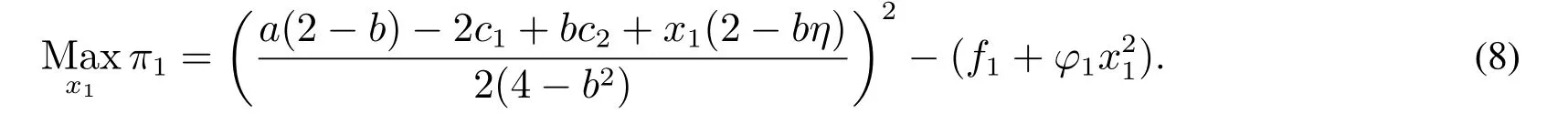
优化式(8),得到OEM 1 的最优流程投资水平.将代入上述关于流程投资水平的最优批发价格、产品需求和收益函数中,得情形IN的模型均衡结果.OEM 2作为唯一投资方,即情形NI下的模型可采取类似的方法建立并求解,不再赘述.两种情形下的模型均衡结果如表1所示.

表1 不同情形下的模型均衡结果Table 1 Equilibrium outcomes of the model under different settings
2.4 OEM都不采取流程投资策略(情形NN)
当两个OEM都不采取流程投资策略时,产品生产成本维持在初始水平.博弈第3和第4阶段,CM 和OEM的收益最大化问题分别满足πi=(pi −wi)qi.采用逆推法求解,得到情形NN下的模型均衡结果,见表1.
3 模型均衡结果分析与OEM的流程投资策略
本节比较不同情形下的模型均衡结果,分析各企业最优决策和收益的变化情况,并给出OEM的最优流程投资策略.然后,讨论搭便车系数、产品替代程度等对最优流程投资策略的影响.
3.1 情形IN(NI)与情形NN的比较分析
首先,比较情形IN(NI)与情形NN下的模型均衡结果,目的在于回答如下问题:与无流程投资的情形相比较,其中一个OEM对共同CM进行流程投资后,各企业的最优决策如何变化? 投资方能否获得更多收益?流程投资对CM和搭便车者又会产生怎样的影响?根据命题1,得如下结论.
定理1与OEM都不采取流程投资策略的情形相比较,单一OEM对共同CM进行流程投资时:
i)CM降低了两个OEM的产品批发价格,但它从销售给各方的产品中获取了更高的边际利润,并获得了更多收益.
ii)投资方的产品需求和边际利润增加.若搭便车系数足够小(η < b/2),搭便车者的产品需求和边际利润减少,否则,它的产品需求和边际利润增加.
定理1的第一部分表明,相对于无流程投资的情形,单一OEM采取流程投资策略时,两个OEM都能以较低的批发价格购买产品,但这并不意味着CM的利益会遭受损失.原因在于,无论是受流程投资的直接影响还是受搭便车行为的间接影响,两种产品的生产成本都得到了改善,因而批发价格降低.一方面,生产成本的减少幅度高于批发价格的降低幅度,CM获得了更高的边际利润.另一方面,投资方的产品需求得以提升,增加了CM的收益.对搭便车者而言,当搭便车系数较大时,流程投资大幅改善了它的产品生产成本.此时,CM会设定较低的批发价格.相应地,搭便车者降低了零售价格并扩大了产品需求,有助于改善CM的收益.当搭便车系数较小时,搭便车者的产品生产成本降低幅度不是特别明显.产品批发价格和零售价格均处于较高水平,不利于产品需求的增加.总体上来看,与搭便车者的产品需求减少对CM的影响相比较,产品边际利润的增大、投资方产品的需求增加等综合因素的影响更强,使CM获得了更多收益.
定理1的第二部分给出了流程投资对两个OEM最优决策的影响.投资方通过流程投资降低了产品生产成本,由该定理的第一部分可知,CM会为其设定更低的批发价格.投资方也会为消费者设定较低的零售价格,从而扩大产品需求.但投资方的零售价格降低幅度低于CM的批发价格减少幅度,换言之,投资方并没有把CM的让利毫无保留地给予消费者,非完全的价格转嫁[34]为它带来了较高的边际利润.当搭便车系数足够小时,搭便车者无法从流程投资中获得较多好处.一方面,投资方的产品生产成本改善得如此显著以至于产生了更多的有效需求.另一方面,搭便车者为吸引更多消费者,降低了自己的零售价格.但受限于较低的生产成本改善幅度,降价对其产品需求的影响效果不太明显.两方面因素共同导致搭便车者在较小的搭便车系数下获得了较低的有效需求.此外,搭便车者迫切希望通过低价吸引消费者、应对投资方的成本竞争,它的零售价格降低幅度会高于CM的批发价格减少幅度.换言之,搭便车者将CM的让利超额给予了消费者,这种过度的价格转嫁[34]使它获得了较低的边际利润.
根据定理1可知,流程投资能够实现投资方的边际利润和产品需求的双重改善,这是否意味着它一定能从投资中获得更多收益?为回答该问题,比较表1中情形NN和情形IN(NI)下OEM的最优收益,得如下结论.
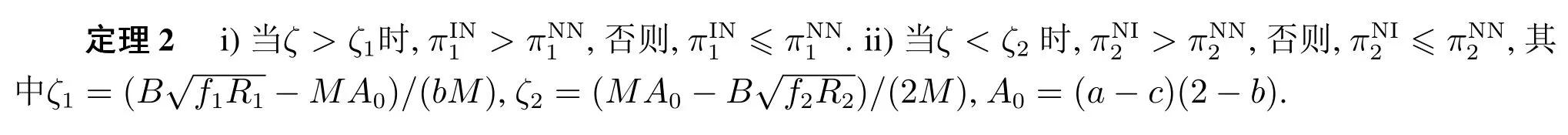
定理2说明,给定对手不采取流程投资策略,OEM是否愿意对共同CM进行流程投资取决于产品初始生产成本之差(ζ).对OEM 1 而言, 当ζ大于ζ1时它才会投资.从以下两个层面解释.若ζ >max{0,ζ1}, OEM 1拥有产品初始生产成本优势,采取流程投资策略后它仍能维持成本优势.若ζ1< ζ≤0,OEM 1 处于产品初始生产成本(弱)劣势地位,但不是特别明显.并且,流程投资能够帮助OEM 1摆脱这种劣势.因此,OEM 1采取流程投资策略能够达到巩固成本优势或者缓解成本劣势的效果.前一种情况下,OEM 1 的收益势必得到改善;后一种情况下,由定理1 可知,OEM 1 的产品需求和边际利润都增加,它们对其收益的积极影响超过了投资成本的消极影响.类似地,当ζ小于ζ2时,OEM 2 才能从自身的流程投资中获得更多收益.
3.2 情形II与情形NI(IN)的比较分析
本节比较情形II与情形NI(IN)下的模型均衡结果,分析一个OEM对共同CM进行流程投资时,其对手的流程投资策略选择对各博弈方最优决策和收益的影响.首先,讨论OEM 2对共同CM 进行流程投资的情况下,OEM 1采取和不采取流程投资策略时各企业的最优决策变化情况.根据命题1,得如下结论.
定理3与情形NI相比较,情形II下,有下列结论:
i)CM降低了OEM 1的产品批发价格,并从销售给它的产品中获取了更高的边际利润.若搭便车系数较小,CM将提高OEM 2的产品批发价格,但从销售给它的产品中获取的边际利润减少;否则,CM将降低OEM 2 的产品批发价格并从中获取较高的边际利润.
ii)OEM 1的产品需求和边际利润增加.当搭便车系数较小时,OEM 2的产品需求和边际利润减少;否则,它的产品需求和边际利润增加.
定理3的第一部分说明,给定OEM 2对共同CM进行流程投资,OEM 1采取流程投资策略时能够获得更低的批发价格.在流程投资和搭便车效应的双重影响下,OEM 1的产品生产成本得以显著改善,并且改善幅度高于批发价格的减少幅度,因而CM从销售给它的产品中获取了更高的边际利润.若OEM 2 从对手的流程投资中获得的好处不多,即搭便车系数较小时,它的产品生产成本无法得到进一步改善,批发价格将维持在较高水平.从整体上来看,批发价格的变化幅度不如产品生产成本的变化幅度明显,CM 无法从销售给OEM 2 的产品中获取更多的边际利润.该定理的第二部分给出了OEM 1的流程投资对它自身和对手的最优决策的影响.OEM 1采取流程投资策略后, 由于产品生产成本和批发价格都会降低, 它不必同等程度地降低零售价格即可达到扩大产品需求的目的,这种非完全的价格转嫁为它带来了更高的边际利润.当OEM 2无法从OEM 1的流程投资中获得足够多好处时,根据定理3的第一部分可知,它的产品批发价格相对较高,与之相应的是较高的零售价格和较低的产品需求.为了吸引消费者并有效应对对手的成本竞争,OEM 2 不会大幅提升零售价格.因此,即使付给了CM更多的产品购买成本,OEM 2也没有把增加的购买成本以更高的零售价格的形式让消费者为其完全埋单,该形式的价格转嫁使它获得了较低的边际利润.
下面,分析OEM的最优收益.比较表1中OEM在情形II和情形NI(IN)下的最优收益,得如下结论.
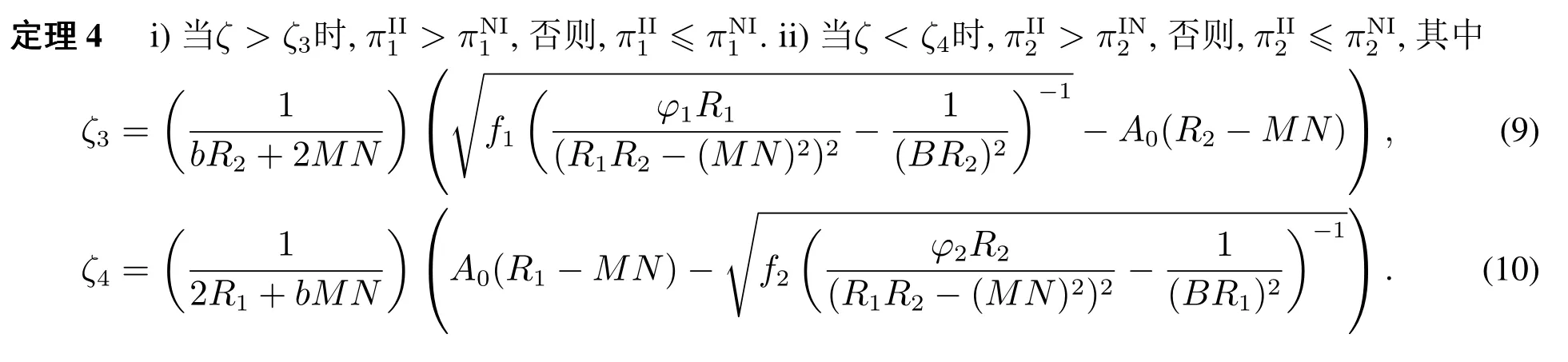
定理4给出了对手采取流程投资策略时, OEM愿意对共同CM进行流程投资的条件.给定OEM 2投资, 当ζ大于ζ3时, 与仅扮演搭便车者的角色相比, OEM 1作为投资方将获得更多收益, 原因如下.若ζ >max{0,ζ3},OEM 1相对于对手拥有产品初始生产成本优势.此时,OEM 2 采取投资策略会削弱OEM 1的成本优势,OEM 1 有动机通过流程投资维持或强化成本优势.根据定理3,采取流程投资策略后,产品需求和边际利润均增加,OEM 1 获得了更多收益.若ζ3<ζ≤0,OEM 1处于产品初始生产成本(弱)劣势地位.OEM 2采取流程投资策略时会把OEM 1 推向较为明显的成本劣势地位.OEM 1有动机进行流程投资来摆脱该局面,使自己不至处于更为严重的成本劣势而受损.尽管需要付出流程投资成本,但OEM 1的产品需求和边际利润均增大,并在影响其收益的过程中占据主导作用,最终改善了它的收益.综上所述,当ζ大于ζ3时,OEM 1 才会对共同CM进行投资.OEM 2 是否愿意采取流程投资策略取决于阈值ζ4,原因与上述分析类似.
3.3 综合比较分析及最优流程投资策略
在两两比较的基础上, 本节做综合比较, 分析OEM的流程投资博弈均衡, 讨论搭便车系数等因素的影响.由于定理1~定理4中的阈值ζk(k=1,2,3,4)较为复杂,采用数值仿真的方法分析.基本参数赋值a=10,c= 5,fi= 0.1,φi= 0.5,b= 0.65, 搭便车系数(η)作为自变量从0增加到1.此外, 为探讨产品替代程度(b)对流程投资博弈均衡的影响, 令η={0.4,0.6,0.8},b作为自变量从0增加到1, 结果如图2~图5所示.令Ξ1=max{ζ1,ζ3},Ξ2=min{ζ2,ζ4},联合表2中的收益矩阵,得如下结论.

表2 两个OEM的收益Table 2 The two OEMs’profits
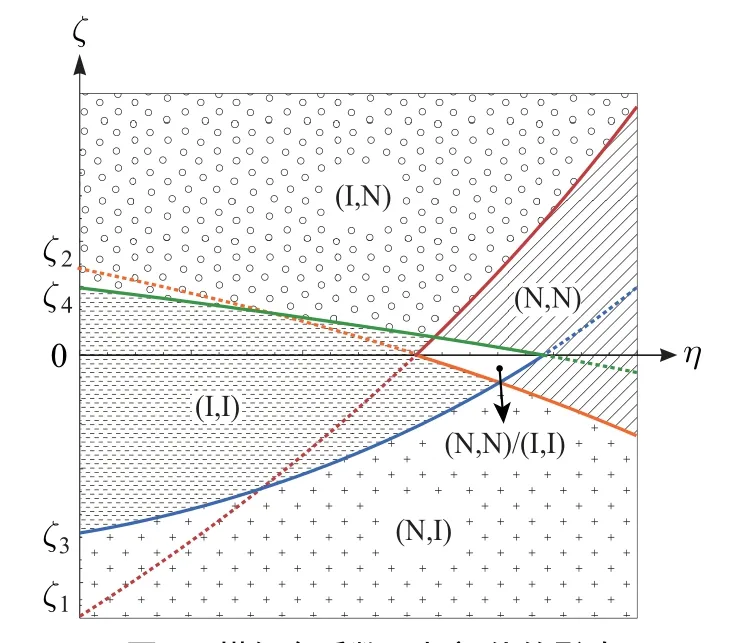
图2 搭便车系数η对ζ阈值的影响Fig.2 Impact of η on ζ thresholds

图3 产品替代程度b对ζ阈值的影响(η =0.4)Fig.3 Impact of b on ζ thresholds(when η =0.4)
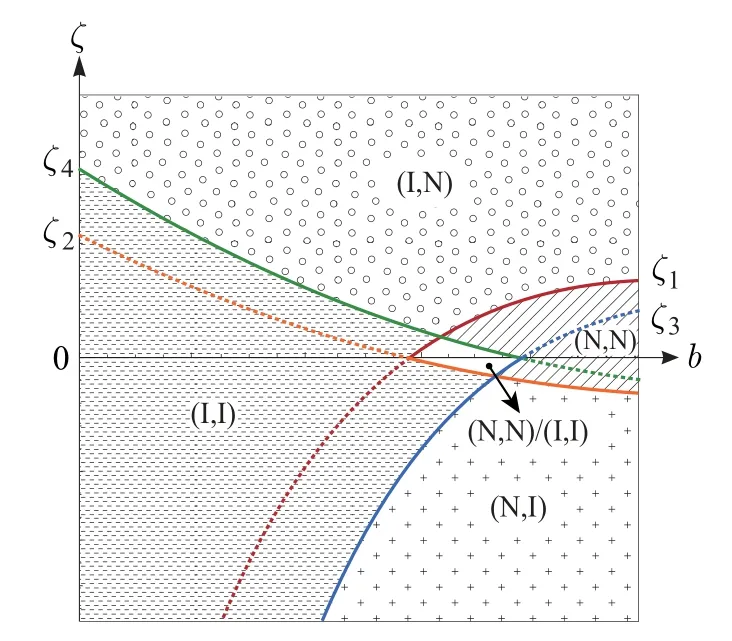
图4 产品替代程度b对ζ阈值的影响(η =0.6)Fig.4 Impact of b on ζ thresholds(η =0.6)

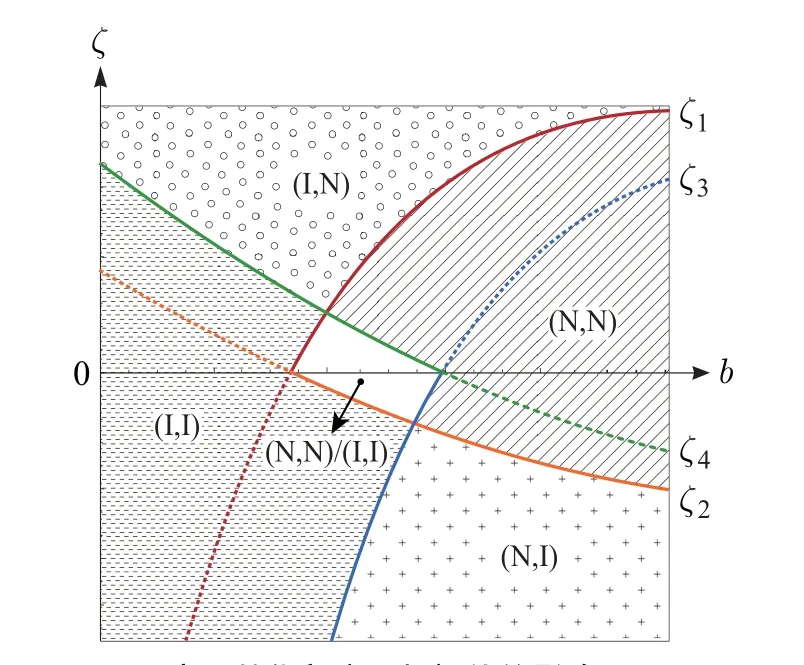
图5 产品替代程度b对ζ阈值的影响(η =0.8)Fig.5 Impact of b on ζ thresholds(η =0.8)
定理5竞争OEM的流程投资博弈均衡满足的条件是:
定理5表明,两个OEM是否会对共同CM进行流程投资不仅取决于搭便车系数,还受它们的产品初始生产成本之差的影响.当初始生产成本之差足够大时,无论搭便车系数大小如何,拥有成本优势的OEM总会采取流程投资策略,竞争对手仅扮演搭便车者的角色.初始生产成本之差不是很大时,最优流程投资策略取决于搭便车系数: 若搭便车系数较小,两个OEM都会投资;若搭便车系数处于中等水平,二者的最优流程投资策略具有同步性,或者都投资,或者都不投资;若搭便车系数较大,双方都不会投资.原因解释如下.
两个OEM的产品初始生产成本之差很大,意味着一方相对另一方拥有非常显著的成本优势.拥有成本优势的OEM 有动机对CM进行流程投资拉大成本差距、增强成本优势.处于成本劣势的一方即使采取流程投资策略,或者通过搭便车降低产品生产成本,也无法扭转固有的成本劣势局面.此外,流程投资成本进一步弱化了投资积极性,导致它与对手的产品生产成本差距愈发明显.因此,两个OEM的产品生产成本将呈现出“马太效应”: 拥有成本优势的OEM愿意投资,成本优势越来越显著;处于成本劣势的OEM仅选择搭便车,成本劣势越来越严重.
两个OEM的产品初始生产成本之差不是很大,说明一方不会具有明显的成本优势.若搭便车系数小,每个OEM都无法从对手的流程投资中获得较多好处,任何不采取投资策略的一方都将处于成本劣势地位,并遭受产品需求和收益的损失.因此,两个OEM都会投资.若搭便车系数大,OEM的流程投资在降低自己的产品生产成本时,也大幅改善了对手的产品生产成本.由于产品初始生产成本相差不大,改善后的产品生产成本也大致相当.换言之,较大的搭便车系数消除了任何一方通过流程投资获取更强成本优势的可能.双方的成本竞争仍处于势均力敌状态,流程投资对产品需求的影响不是特别明显,两个OEM无法从投资中获得更多收益,因而都不投资.若搭便车系数中等,OEM 的流程投资不会过多地降低对手的产品生产成本.一方面,产品初始生产成本差距不大,OEM 进行流程投资后能大幅独享流程投资的好处.由于投资决策为公共信息,当另一个OEM无法从搭便车中获得足够多好处时,会进行流程投资以确保自己不处于成本劣势.改善后的产品生产成本为投资方带来了更多收益,共同投资构成了博弈均衡.另一方面,中等水平的搭便车系数说明OEM可以从对手的流程投资中获得一定好处.同时,势均力敌的产品初始生产成本意味着任何一个OEM都不会具有绝对的成本优势.即使存在着搭便车,改善后的产品生产成本之差依旧很小,任何一方的价格竞争优势不会特别凸显.最终,产品需求的增加对收益的积极影响不足以弥补投资成本等的消极影响,采取流程投资策略将得不偿失.综上,在中等水平的搭便车系数下,两个OEM都不愿意进行流程投资.
在定理5的基础上,进一步探讨如下问题:两个OEM都采取流程投资策略时,一定比它们都不投资时获得的收益多吗? 比较命题1中情形II和情形NN下OEM的最优收益,得如下引理.
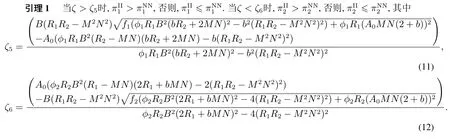
引理1表明,与无流程投资的情形相比,若OEM 1 拥有显著的产品初始生产成本优势,它能够从共同投资中获得更多收益,否则,它将遭受损失.OEM 2 在两种情形下的最优收益之差具有类似特征, 取决于阈值ζ6.由此可见,两个OEM都对共同CM进行流程投资时,它们的最优收益不一定比无流程投资时的高.只有当产品初始生产成本之差处于中等水平(ζ5< ζ < ζ6)时,两个投资方才能从流程投资中获利.值得注意的是,定理5 给出了OEM愿意对CM进行流程投资的条件,这意味着需要将该定理中的流程投资边界条件与引理1中的阈值进行比较,才能给出情形II和情形NN下OEM最优收益的变化状况.由于ζ阈值的复杂性所致,仍采用数值仿真的方法分析.基本赋值保持不变,结果如图6所示,由此可得如下结论.
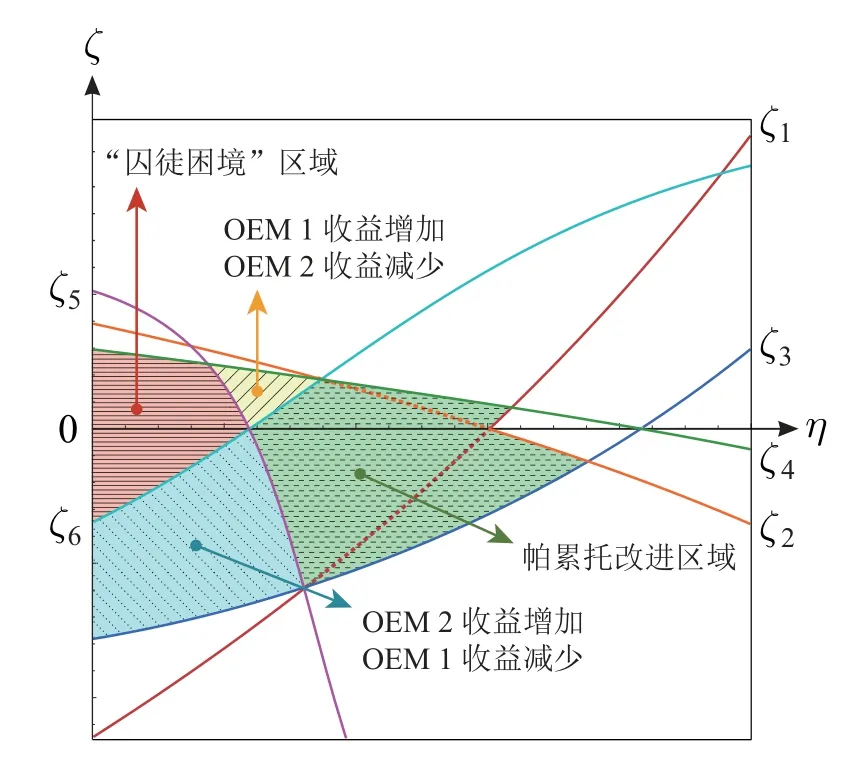
图6 情形II与情形NN下OEM的最优收益比较Fig.6 Comparison of the OEMs’optimal profits in Case II and Case NN
定理6情形NN相比较,情形II下,两个OEM的最优收益变化状况如下:

定理6给出了情形II下两个OEM的最优收益相对于情形NN下的变化状况.根据该定理并结合图6可知,均衡状态下,当OEMi相对于对手拥有显著的产品初始生产成本优势,即ζ足够大(小)时,共同投资能为OEMi带来更多收益对手的收益会遭受损失当产品初始生产成本之差中等时,若搭便车系数较小,两个投资方的收益减少,否则,它们的收益增加.原因分析如下.
两个OEM都采取流程投资策略时,拥有显著的产品初始生产成本优势的一方,能够通过直接的流程投资和间接的搭便车降低自己的产品生产成本,继续维持成本竞争优势并从中获得更多收益.均衡状态下,尽管处于产品初始生产成本劣势的OEM的收益减少,但它还是会采取流程投资策略,否则,将遭受更多的利益损失.当产品初始生产成本之差中等时,两个OEM的产品初始生产成本相差不大,任何一方都不会比对方拥有十分明显的成本优势.此时,若搭便车系数很小,两个OEM均无法从对方的流程投资中获得更多好处,改善后的产品生产成本相差无几并仍处于较高水平,这会形成较高的批发价格和零售价格,弱化消费者购买的积极性.较低的产品需求不利于OEM收益的增加.同时,流程投资成本进一步拉低了它们的最优收益,导致两个投资方得不偿失,从而形成流程投资“囚徒困境”.当搭便车系数较大时,两个投资方都能从对方的流程投资中获得较多好处,在直接的流程投资和较强的搭便车效应的共同影响下,产品生产成本得以大幅降低,有助于产品需求的提升.尽管两个投资方需要付出流程投资成本,但较低的批发价格和较高的产品需求对它们最优收益的影响占据了主导作用,出现了收益“共赢”局面,实现了帕累托改进.
下面从产品替代程度的视角,分析它对流程投资博弈均衡的影响.此时,阈值ζk为产品替代程度的函数,其中k=1,2,3,4.不同搭便车系数下的结果如图3至图5所示.
定理7产品替代程度(b)和搭便车系数(η)对流程投资博弈均衡的影响满足如下条件:


定理7表明,两个OEM的产品替代程度和产品初始生产成本之差在它们的最优流程投资策略选择中具有重要的影响.产品初始生产成本之差较大时,拥有成本优势的OEM采取流程投资策略,其对手仅选择搭便车,并且它们的选择不受产品替代程度的影响.产品初始生产成本之差不是很大时,若产品替代程度足够低,它们都愿意对共同CM进行流程投资;若产品替代程度足够高,双方都不会采取流程投资策略;中等水平的产品替代程度下,两个OEM 的最优流程投资策略将呈现出同步性.该定理的解释如下.
两个OEM的产品初始生产成本之差较大时,一方比另一方拥有绝对成本优势,并能将该优势转化为定价优势、扩大有效需求.与流程投资成本相比,产品需求的增加对拥有成本优势OEM的收益的影响更强,使其获得了更多收益.尽管处于成本劣势的OEM通过搭便车降低了自身的产品生产成本,但由于它的成本劣势是如此严重,以至于进行流程投资也无法摆脱利益受损的局面.产品初始生产成本之差不是很大时: (i)产品替代程度低.市场竞争不激烈,每个OEM都能通过流程投资减少各自的产品生产成本,产品边际利润和需求得以增加.并且,它们对收益的积极影响强于流程投资成本的消极影响,因而两个OEM都愿意投资.(ii)产品替代程度高.市场竞争激烈,OEM将降低零售价格[35],尽管这会扩大产品需求,但过低的零售价格拉低了产品的边际利润.考虑流程投资成本等,两个OEM采取流程投资策略将得不偿失.(iii)产品替代程度中等.市场竞争不是很激烈,OEM的边际利润不会受损很多.流程投资降低了产品生产成本,促进了产品需求的提升.总体上来看,采取流程投资策略为两个OEM带来了恒为正的净收益.另一方面,中等水平的产品替代程度下,OEM 会降低零售价格.尽管采取流程投资策略的一方的批发价格较低,但其减少幅度仍小于零售价格的降低幅度,投资方的收益受损.综上所述,两个OEM也有可能都不投资.
定义2.2 称伪BCI-代数X上的一个犹豫模糊集为X的一个犹豫模糊交换滤子,如果为X的一个犹豫模糊滤子,且满足对任意x,y ∈ X, 有
值得注意的是,图3~图5还表明,随着搭便车系数的增大,区域(I,I)减少、区域(N,N)/(I,I)和区域(N,N)从无到有并逐渐变大.这说明,当OEM的流程投资为对手带来的好处越来越多时,它们都不采取流程投资策略的可能性越来越高.尤其是随着产品替代程度的增大,无流程投资的可能性进一步提高.原因在于,根据定理5,产品初始生产成本之差不大时,搭便车系数越高,每个OEM的流程投资给对手带来的好处越多,采取流程投资策略的OEM无法获得比对手更为显著的成本优势.在较高的产品替代程度下,激烈的市场竞争迫使两个OEM降低零售价格[35],这会拉低产品边际利润并减少收益,因而它们都不会采取流程投资策略.
4 结束语
生产外包是OEM实现降本增效的有效举措.但一个CM会与多个竞争OEM存在合作关系, OEM对共同CM进行流程投资降低自身的产品生产成本时,流程投资可能会在CM处存在搭便车现象而降低对手的产品生产成本.本文研究了两个竞争OEM能够在共同CM处搭对方流程投资的便车时,它们的最优投资策略问题.运用博弈论的方法构建了四种情形下的模型,分析模型均衡结果,发现拥有产品初始生产成本优势的OEM愿意采取流程投资策略;当两个OEM的产品初始生产成本相差不大时,它们的最优投资策略取决于搭便车程度的强弱.并且,产品替代程度在竞争OEM的最优流程投资策略选择中也有至关重要的影响.均衡状态下,共同投资既有可能使一方获利一方受损,也有可能实现帕累托改进,亦或形成“囚徒困境”.
未来值得研究的方向包括: 一是考虑OEM在流程投资策略选择中,是否有动机进行合作投资;二是纳入私有信息,研究OEM是否应对共同CM 进行投资的问题;三是探讨搭便车系数内生时的流程投资博弈均衡.
附录
命题1的证明


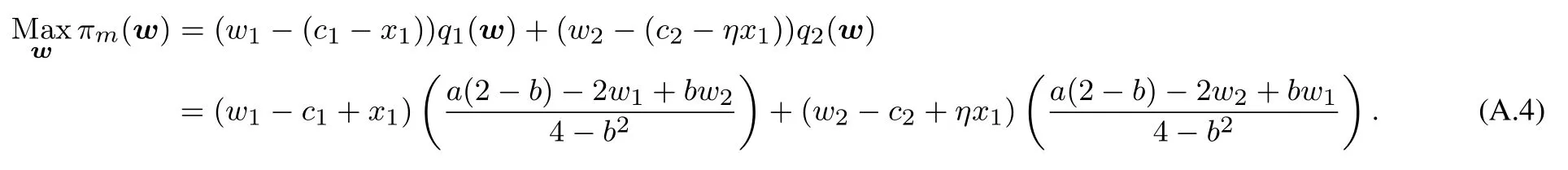

引理1的证明
把表1中情形II与情形NN下每个OEM的最优收益作差,得
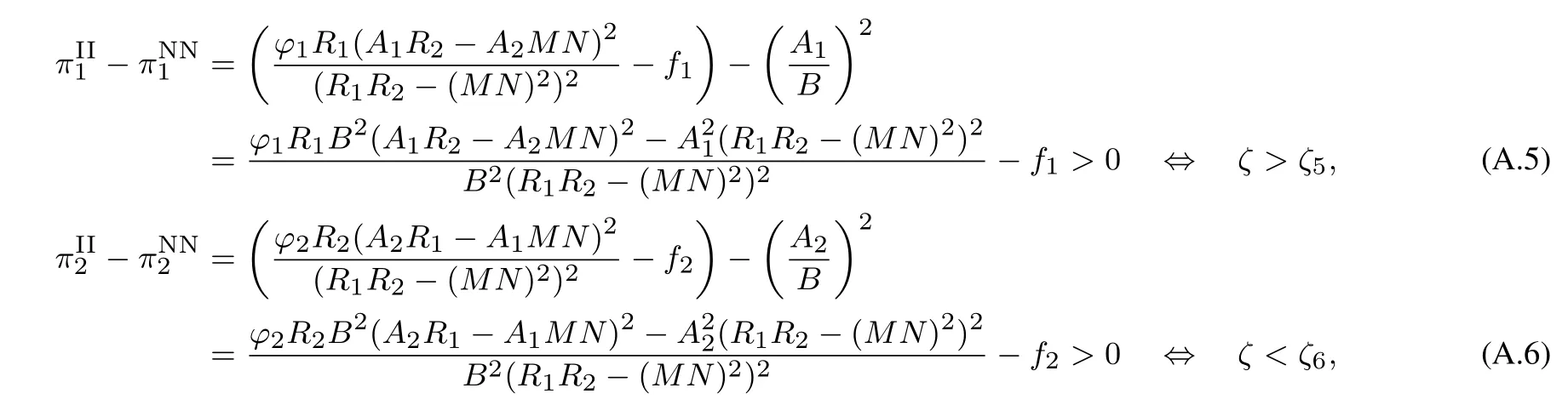
其中ζ5,ζ6的表达式分别如式(11)和式(12)所示. 证毕.
定理1的证明

容易验证,上述边际利润均大于零.将CM在情形IN和情形NN下的最优收益作差,得

第二部分的证明.情形IN与情形NN下每个OEM的最优订购量之差为
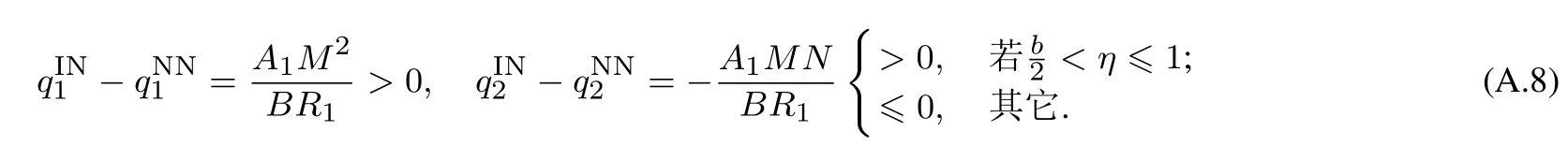
此外,情形IN和情形NN下OEMi的边际利润(i=1,2,ℓ=IN,NN),如式(A.8)所示. 证毕.
定理2的证明
由表1可知,情形IN与情形NN下OEM 1的最优收益之差满足

其中A0=(a −c)(2−b).
OEM 2作为唯一投资方时,情形NI和情形NN下它的最优收益之差满足

证毕.
定理3的证明
第一部分的证明.情形II和情形NI下CM为每个OEM设定的最优批发价格之差为

由上述边际利润表达式,得
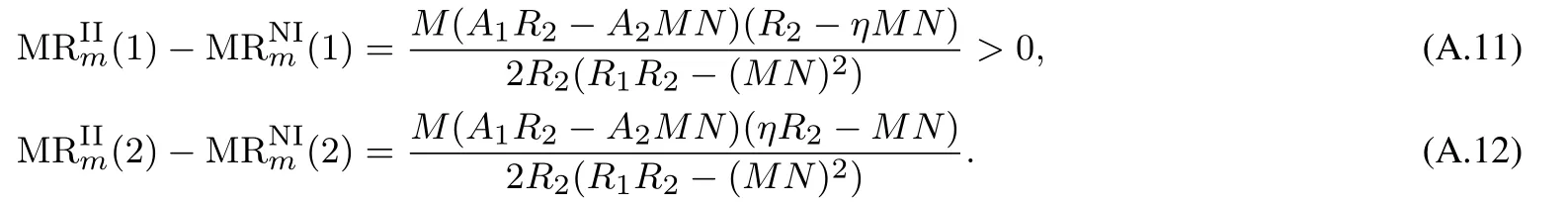
根据最优批发价格的比较分析过程可知,当且仅当η∗<η≤1时,式(A.12)大于零.
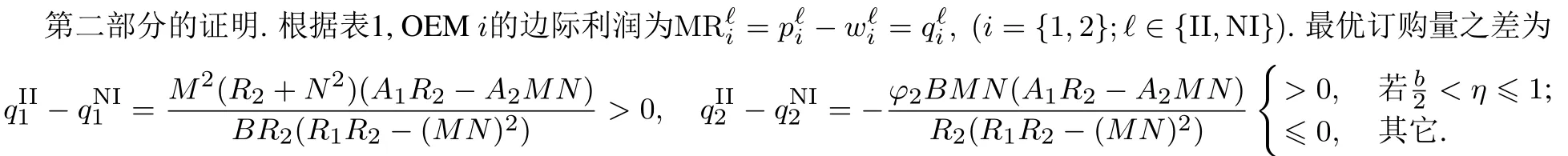
证毕.
定理4的证明
将表1中情形II与情形NI下OEM 1的最优收益作差,得
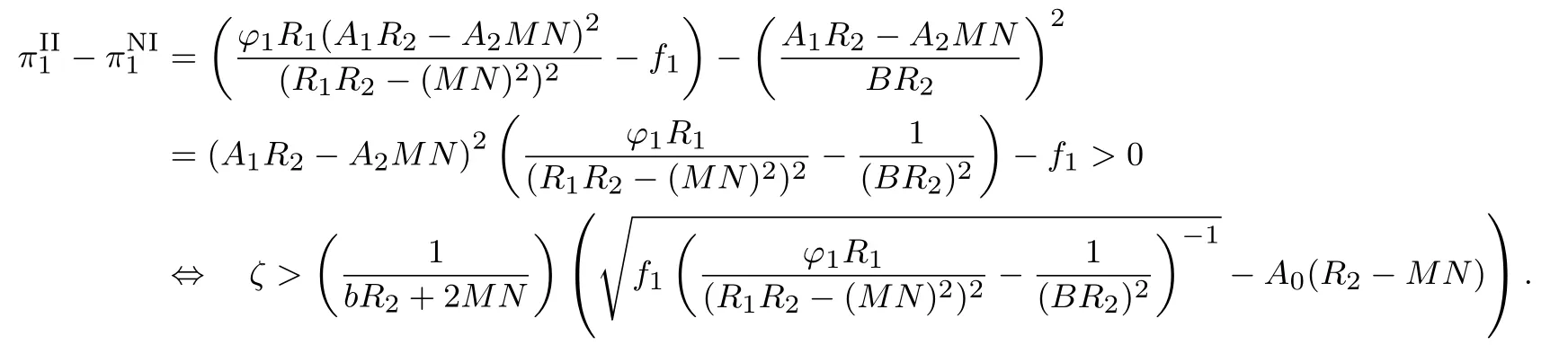
情形II与情形IN下OEM 2的最优收益之差满足
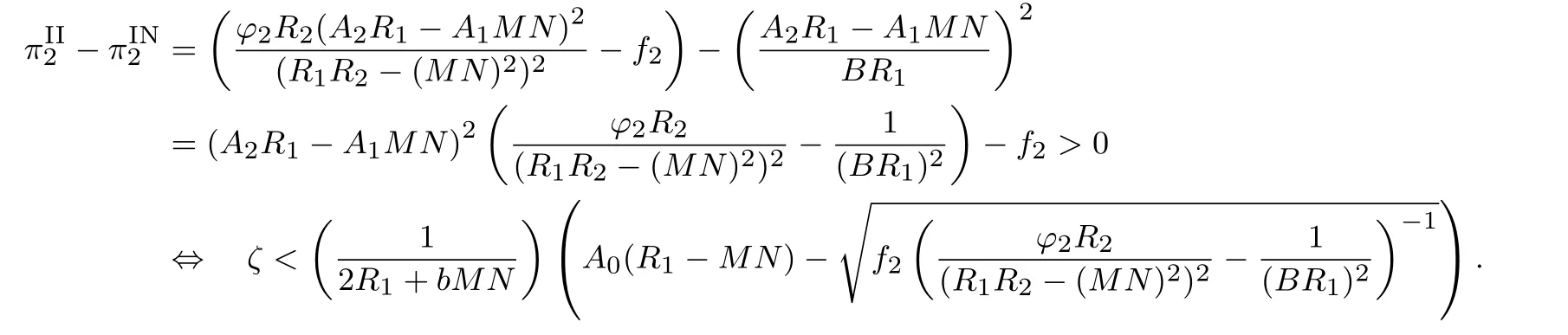
证毕.

