大周期内的相位差优化方法
鄢小文
(浙江机电职业技术学院 智慧交通学院,浙江 杭州 310053)
0 引言
干道信号协调控制在缓解城市干线交通拥堵、减少尾气排放以及提升交通安全等方面具有重要作用。基于此,相关专家学者对干道绿波协调控制方法进行了较为深入的研究,相位差优化的方法主要包括带宽最大、延误最小、结合法、TRANSYT、SIGOP以及SYNCHRO等。其中,带宽最大和延误最小是最常用的两种相位差优化方法。常用的绿波带法有图解法[1]、数解法[2-3]以及模型法[4]。延误最小化[5]是通过建立延误模型,寻找满足延误最小的最优相位差值,常用的主要有延误三角形法、延误四边形法等。
传统的干道绿波信号协调大多以带宽最大为控制目标,期望尽可能多的车辆能够运行在绿波带内,在低饱和状态下能够起到较好的控制效果,大大降低处于绿波带内的车辆的运行延误以及停车次数。以徐建闽[2]教授为代表,针对低饱和状态的城市连续流交通绿波信号协调控制方法的研究已日趋成熟。但多数研究均假定干道各交叉口采用相同的信号周期时长,然而实际线控系统中,干线各交叉口受其交通流量、几何条件、行人过街等因素的影响,各交叉口实际所需信号周期时长往往并不相等。对于该问题,通常采取子区间划分[6]将信号周期相近的交叉口划在同一子区间进行绿波协调控制,然而不同子区之间仍采取不同信号周期时长,这在一定程度上割裂了子区间的联系,降低了绿波协调的效果。
如何满足实际交通信号控制系统的需求,解决同一干道上不同周期子区间的协调控制问题以及如何扩展现有干道绿波协调控制方法以实现路网内不同周期干道间的协调控制显得尤为重要。若上下游交叉口的信号周期相同,优化协调模型可得上下游交叉口间的最优相位差值;但若上下游交叉口信号周期不同,本周期内得到的最优相位差对于下个周期并非最优,仅仅通过模型无法得到大周期控制时段的最优相位差序列值。由于周期不同,交叉口之间的相位差周期性变化导致交叉口间的车流到达分布也呈现周期性的波动现象。因此本文针对信号周期不同的上下游交叉口间的相位差优化方法展开深入研究,将信号协调控制方法扩展应用到周期不等的信号交叉口间的协调问题中,提出了大周期内的相位差优化方法。
1 研究对象
如图1所示,上、下游两个相邻的信号交叉口周期时长分别为CU和CD,路段长度为L,车辆在路段上行驶的平均速度为ν,协调相位绿灯时长分别为gU和gD,红灯时长分别为rU和rD,相位为对称放行。忽略右转车流的影响,上行方向车流由西进口直行以及北进口左转车流构成,下行方向车流由东进口直行以及南进口左转车流构成。
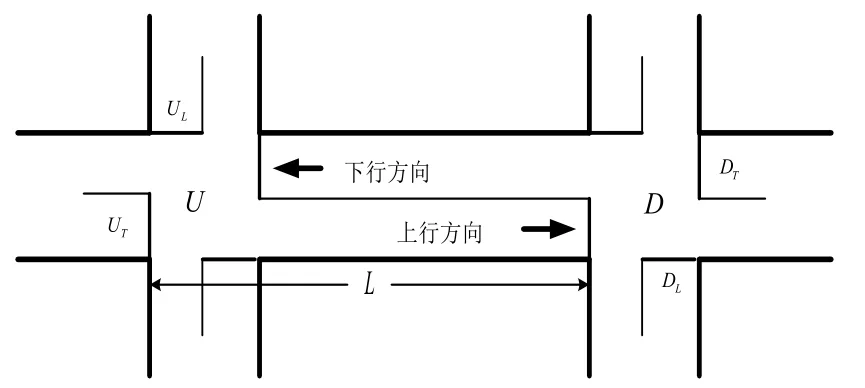
图1 相邻交叉口间路段示意Fig 1.The road segment between adjacent intersections
为了简化建模过程,提出几点假设:
(1)上游交叉口为固定信号配时,绿灯时间被充分利用;
(2)协调相位绿灯期间直行车流以饱和流率释放,红灯期间左转车流以稳定流率到达;
(3)初始时刻停车线处排队长度为0,初始周期队列完全消散,后续周期无二次排队;
(4)不考虑车流的离散性以及右转车辆的影响。
2 大周期内的相位差优化方法
2.1 大周期时距图
本文探讨周期不同的信号交叉口之间的协调问题,故定义一个大周期,取值由上下游信号交叉口周期的最小公倍数确定。假设两信号交叉口周期近似满足关系:

n1、n2均为正整数,定义大周期的控制时段:

假定上、下游交叉口的信号周期分别为CU、CD(CU≠CD),由于周期时长不同,以交叉口D为基准,每过一个周期CD,它与交叉口U之间的相位差向一个方向偏移

定义一个大周期控制时段,满足T=n1·CU=n2·CD,在控制时段T内,需要确定n1个步序的相位差值,每经过一个步序对相位差进行优化更新。如图2所示为大周期时段内上下游交叉口间的时距图。

图2 大周期时段内上下游交叉口间的时距图Fig 2.Time interval between upstream and downstream intersections during large cycle
假定初始时刻正向上下游交叉口间的相位差为φ0,此处探讨的相位差如无特别说明均为相对相位差,指下游交叉口D指定相位绿灯起始时刻滞后于上游交叉口相位绿灯起始时刻的时长,则在大周期时段内正向上下游交叉口间的n1个步序的相位差值依次为:

对应的大周期时段内反向上下游交叉口间的n1个步序的相位差值依次为:
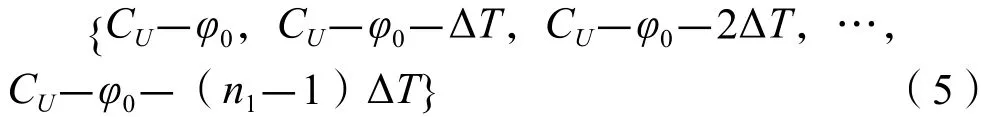
当经过一个大周期后,两交叉口之间的相位差又回到初始状态,相位差的循环周期为T,控制时段每循环一次,就依次运行n1个步序的相位差值。
2.2 相位差优化算法
为了解决不同周期信号交叉口间协调控制的需要,本文以大周期为控制时段,研究在大周期时段内保证系统的运行最优,即车流的总延误最小。分析可知,大周期时段内每个控制步序下相邻交叉口之间的相位差与大周期时段初始时刻的相位差φ0息息相关,每个步序的相位差值存在如下关系:


其中,φ1,φ2,…,φn1分别为第k个步序相邻两交叉口之间的正向相位差,φ1',φ2',…,φn1'分别为对应的反向相位差。为了实现大周期内总延误最小,需要综合考虑n1个步序的延误与相位差关系。大周期内的相位差优化流程如图3所示,优化详细步骤如下:
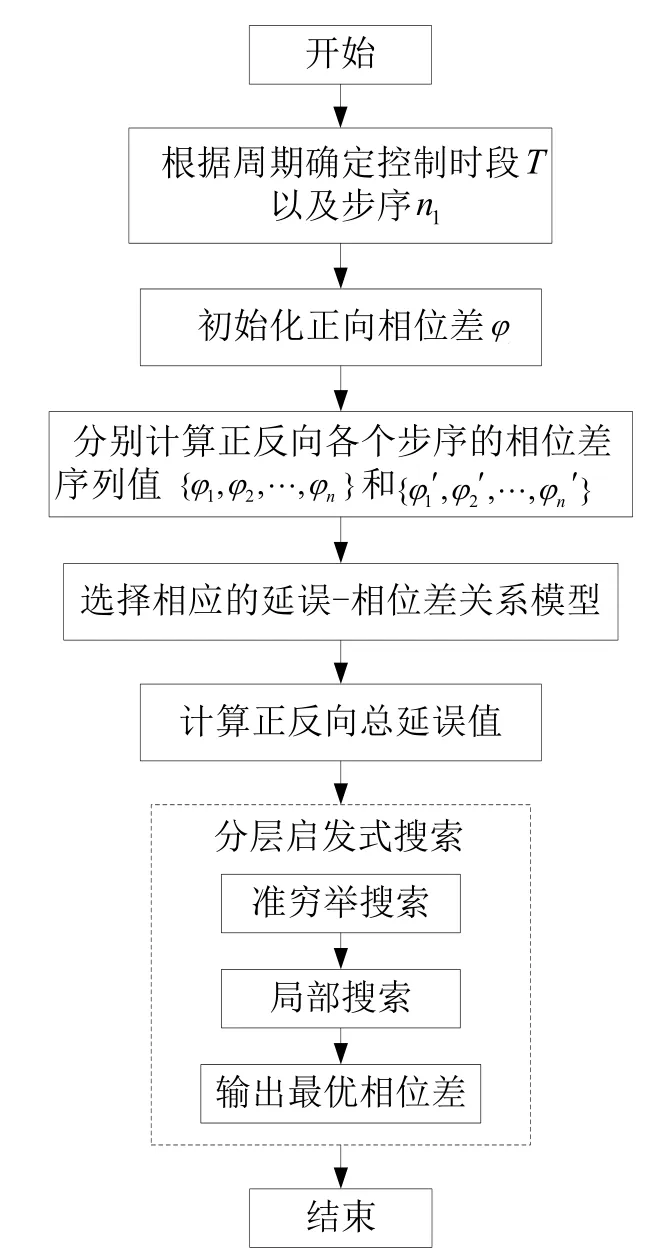
图3 控制时段内相位差优化流程Fig 3.The process of phase difference optimization during control period
Step1:根据周期确定控制时段T以及该时段的步序数n1;
Step2:初始化大周期时段正向的初始相位差φ0,根据φ0计算大周期时段各个步序的正反向相位差序列值 {φ1,φ2,…,φn1} 和 {φ1',φ2',…,φn1'},根据相位差序列取值,选取各自对应的延误-相位差关系模型,计算大周期内正反向的总延误值。
Step3:采用分层启发式搜索方法搜索最优相位差,分两步实现:
① 准穷举搜索,即粗搜索
(a) 以20秒为间隔确定低分辨率的搜索空间{-60,-40,-20,0,+20,+40,+60};
(b) 正向相位差在搜索空间中取值,计算并比较每个可能相位差取值下的双向总延误值;
(c) 选择双向总延误取值Dco最小时的正向相位差值φc0。
② 局部搜索,即细搜索
(a)假定j=1,j∈ [1,19],j∈ Z,φcj=φc(j-1)- 1,计算正向相位差取φcj时的总延误值Dcj,j=j+1迭代更新,循环计算Dcj值直至j=19为止,比较Dcj值,选取最小的延误值Dcop=min{Dcj}对应的相位差为最优相位差的可取选项φcop;
(b) 假定j=1,j∈ [1,19],j∈ Z,φcj=φc(j-1)+1,计算正向相位差取φcj时的总延误值Dcj,j=j+1迭代更新,循环计算Dcj值直至j=19为止,比较Dcj值,选取最小的延误值Dcop'=min{Dcj}对应的相位差为最优相位差的可取选项φcop';
(c)比较Dcop与Dcop'的大小,选取延误的较小值Dop=min{Dcop,Dcop'}对应的相位差为最优相位差。
3 相位差动态调整方法
相位方案的过渡是个动态调整的过程,为了保障交通流的平稳安全运行,在控制时段的步序内每次相位差的变化适宜在小范围内进行。根据上下游交叉口之间的周期关系定义大周期控制时段,通过优化大周期初始时段的相位差实现整个控制时段正反向总延误最小的目标。每经过一个大周期时段,需要进行一次相位差的调整。由于周期不变,若只针对两个信号交叉口,则仅需调整一个相位差,只要保证每次相位差的变化在小范围内进行即可;若针对三个或更多个信号交叉口,则需同时调整多个相位差,为了避免不同交叉口的相位差调整时间先后相差较大,需要确定相位差调整量的最优值,尽量使调整比较均匀。相位差动态调整中主要涉及相位差调整量以及调整周期时长这两个关键参数的取值。
3.1 控制方案过渡原理
若针对n个交叉口,控制时段定义为n个交叉口信号周期时长的最小公倍数,即满足:

其中,T为大周期控制时段,n为交叉口个数,T1,T2,…,Tn和n1,n2,…,nn分别为n个交叉口的周期时长以及在大周期内的控制步序数。
随着交叉口个数的增多,大周期控制时段的取值迅速增大,若大周期时段过长,探讨大周期时段内交通运行最优意义不大。因此本方法适用于较少的信号交叉口之间的相位差优化问题。将第一个交叉口作为基准交叉口,此处探讨的相位差如无特别说明均为相对相位差,分别指各交叉口指定相位绿灯起始时刻滞后于基准交叉口相位绿灯起始时刻的时长。图4为控制方案的过渡原理图。

图4 控制方案过渡原理Fig 4.The transition principle of control scheme
假定旧控制方案中大周期控制时段内各个交叉口的初始相位差构成的相位差向量为:

各个交叉口在n1个步序的相位差满足
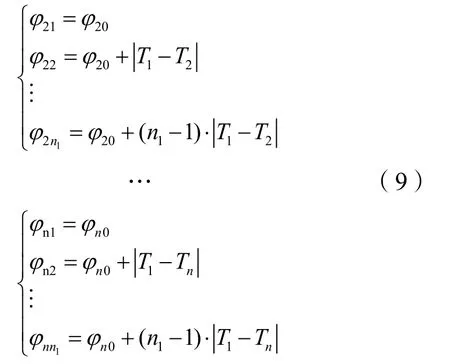
其中,φi1为旧方案中第i个交叉口相对于第一个交叉口大周期控制时段的初始相位差,取值为φi0,i=2,3,…,n。
为了防止信号控制方案的切换对交通流正常运行产生干扰,在方案切换期间一般会加入适当的过渡时间。如下定义过渡时间:
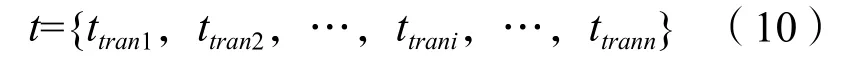
ttrani为第i个交叉口的过渡时间,t为过渡时间向量。
增加过渡时间后,新控制方案中大周期控制时段各个交叉口的初始相位差构成的相位差向量为:
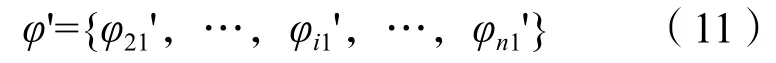
各个交叉口在n1个步序的相位差满足:

其中,φi1′为新方案中第i个交叉口相对于第一个交叉口大周期控制时段的初始相位差,取值为φi0′。
由于大周期时段内的相位差序列值由初始相位差以及上下游交叉口间的信号周期差决定,大周期时段内各个步序的相位差调整量均与初始步序的相位差调整量保持一致,故只要保证初始步序各个交叉口之间的相位差调整量均匀即可,即新旧控制方案的相位差调整量为:

其中:
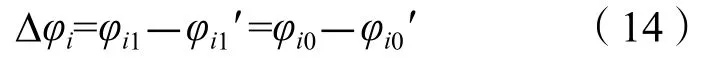
Δφi为第i个交叉口相对于第一个交叉口大周期控制时段的初始相位差以及随后各个步序的相位差调整量。
3.2 相位差动态调整算法
过渡方案的目的是使相位差调整量在过渡周期内逐渐减小到0。由于Δφ中最大元素值与最小元素值可能相差较大,若以Δφ为调整量,可能出现有些交叉口在两个周期内完成调整,而有些交叉口需要超过三个周期才完成调整,这会严重影响干线信号控制的效果。因此,有必要寻找合适的相位差调整量,使各个交叉口方案过渡的时间相近。
令Δφmax和Δφmin分别为Δφ中元素的最大值和最小值,Δφmid为两者均值,即
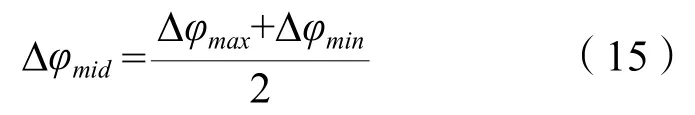
若将Δφ中每个元素同时减去Δφmid得到

其中:

Δφ′为第i个交叉口最终的相位差调整量。
根据式可知,Δφ′∈ [Δφmin-φmid,Δφmax-φmid],Δφi′中相位差调整量的最大值与最小值的绝对值相等,各个交叉口的相位差调整量相对均匀,并能够保证各个交叉口的调整周期相差不大。
调整周期时长与交叉口信号周期允许的调整空间密切相关。假定交叉口信号周期允许取值范围为[Tmin,Tmax],调整方案信号周期的允许调整空间为[Tmin-T,Tmax-T],记为 [ΔTmin,ΔTmax]。
为了尽量减小信号调整过程中的交通流干扰以及缩短调整时间,本文提出了不超过3个信号周期的相位差快速平滑过渡方法,通过比较各交叉口最终的最大相位差调整量Δφmax′以及最小相位差调整量Δφmin′分别与交叉口信号周期允许调整空间的大小关系,确定调整周期个数以及最佳调整周期时长。
(1)单周期调整

(2)双周期调整
若满足 ΔTmax< Δφmax′≤ 2ΔTmax或 2ΔTmin≤ Δφmin′<ΔTmin,可采用双周期过渡,调整周期时长为:

ttrani_1、ttrani_2分别为双周期调整中的第一、二个过渡周期时长。
(3)三周期调整
若满足 Δφmax′> 2ΔTmax或 Δφmin′< 2ΔTmin,可采用三周期过渡,调整周期时长为:
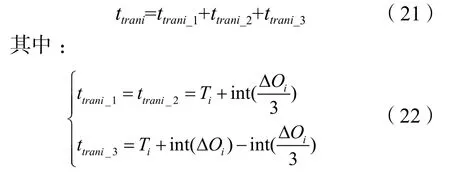
ttrani_1、ttrani_2、ttrani_3分别为三周期调整中的第一、二、三个过渡周期时长。
相位差动态调整算法详细步骤如下:
Step1:根据新旧控制方案的相对相位差计算相位差调整量向量Δφ;
Step2:计算Δφ元素中最大值和最小值的均值Δφmid;
Step3:计算各个交叉口最终的相位差调整量Δφ′;
Step4:根据交叉口的最大相位差调整量Δφmax′以及最小相位差调整量Δφmin′确定调整周期个数以及最佳调整周期时长。
相位差动态调整算法流程如图5所示。
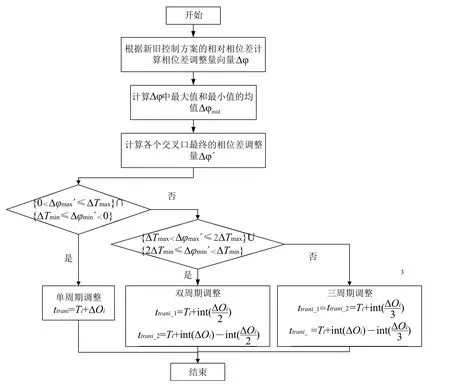
图5 相位差动态调整流程Fig 5.The dynamic adjustment process of phase difference
4 结语
本文考虑到不同周期信号交叉口间协调的需求,提出了大周期内的相位差优化方法以及相位差动态调整方法。此方法的提出弥补了由于子区周期时长不同而导致子区被割裂后绿波协调效果大大降低的缺陷,突破了原有协调模型要求交叉口信号周期长度必须相同的限制。可将此方法推广应用到不同周期干道的信号协调中,真正实现由干线扩展到整个区域的交通信号协调中,故本文提出的大周期内的相位差优化方法对于改善区域路网的交通运行具有重大实际意义。

