基于融合降维-集成学习的两阶段辛烷值预测算法设计研究
郇钫策,江 驹,余朝军,徐海燕
(1. 南京航空航天大学 自动化学院,江苏 南京 211106;2. 南京航空航天大学 经济与管理学院,江苏 南京 211106)
汽油辛烷值是表征汽油各项性能最重要的指标之一,成品汽油中保留的辛烷值越高,汽油的有效利用率也相应的越高,汽车尾气排放量也会相应减少,带来的经济与环境效益也越高[1]。因此,人们希望通过分析石油裂解汽油过程中的各项指标,在石油加工前及时预测出成品汽油中的剩余辛烷值,以避免不必要的经济损失,提高汽油的经济效益[2]。然而,在实际工程中,裂解过程记录的数据维度非常大,各项操作变量之间具有相互强耦合关系以及高度非线性关系,给辛烷值的预测造成了很大阻碍[3]。同时,如果仅仅依靠现有的化工技术(辛烷值试验机、近红外光谱等)对辛烷值进行预测[4],不但存在着检测数据维度庞大的问题,而且还要面临化学实验步骤繁多、所需要的人工及设备费用昂贵的难题[5]。所以,如何高效地解决石油数据高维的问题以及如何采用更优的算法准确预测汽油中的辛烷值成为了国内外诸多学者研究的热点。
现有的研究大多都将目光聚焦于高维数据的预测问题上。在早期研究中,多数文献尝试运用不同的机理、算法对高维数据进行过滤,降低数据的维度。许赟娟等[6]从自变量之间的相关性着手,提出了基于变量聚类的主成分Lasso降维算法。在传统主成分分析法(Principal component analysis,PCA)的基础上,ADNAN等[7]建立了零噪声抑制的PCA模型对特征根和奇异值进行重新分解,最大程度地压缩了含有高信息量的数据。近几年随着机器学习的蓬勃发展,采用各类监督学习、非监督学习来解决高维度问题的思路也逐渐进入人们视野。LIU等[8]提出了基于Kernel principal component analysis降维和XgBoost预测负荷的方法。WANG等[9]利用PCA筛选特征,将数据输入到XgBoost模型中,对销量进行了预测。CHEN等[10]采用主成分分析法神经网络模型(Principal component analysis back propagation,PCA-BP),对汽油中辛烷值的变化进行了预测。
以上对各类算法的研究,虽然极大地丰富了高维数据预测的解决方法,但对于汽油辛烷值这一高维度工业数据的实用性能的作用是有限的。例如主成分Lasso降维算法只针对稀疏模型进行了数据模拟,自行生成的数据与现实数据差距较大,且对数据的线性要求很强,没有考虑到数据存在非线性的情况,算法的鲁棒性和普适性仍留有较大提升空间。主流的PCA降维算法有着对特征的重构和特征的压缩,使得降维后的数据特征在现实中不具有可解释性。另外,文献[9-10]中提出的各类机器学习模型多数都存在复杂度的冗余,加之数据经过PCA的高维投影,数据结构变得简单而预测模型过于复杂,导致模型对于数据的泛化能力减弱[11],只在极端情况下模型的预测效果才有较好的表现[12],不具有强鲁棒性。
基于对前人研究结果的分析,本文首先详细解释互信息法回归(Mutual information regression,MIR)-递归嵌入式特 征 选 择(Embedded feature selection,EFS)的融合降维方法和公式推导;然后利用优化后的预处理流程对现有的汽油数据进行处理;最后基于自适应寻优的集成学习(Ensemble learning)算法建立辛烷值预测模型,并对模型预测结果进行详尽地分析和总结,以期为进一步的研究提供参考。
1 基于融合降维-集成学习两阶段的算法设计
1.1 融合降维算法设计
传统的互信息法回归主要用于计算离散变量之间的相关度,文献[13]利用灰度统计离散特征的互信息量来加快匹配速度;文献[14-15]利用通过k-近邻降维算法将连续变量合并到离散的“分箱”中。上述“分箱化”的思路对采样的程度有很苛刻的要求,分箱的数目需要经过大量的寻优后才能得出,k-近邻降维算法中的参数没有明确的数学定义,导致该算法只在参数均为正整数时才有效。本文基于文献[14]中对互信息法回归估计值的计算方法进行了优化处理,提出了一种新的降维算法,以减少后续预测处理的计算量,为同类技术提供可参考的算法支持。
记X为某一特征变量,Y为标签变量,互信息度量了两个变量共享的信息,已知X,对Y的不确定性减少的程度,用I(X,Y)表示。为了表示不确定性,引入熵这一概念,用符号H(X)表示。对于X有:其中,x表示变量X的数值;p(x)表示X等于x的概率。考虑到X和Y的连续性,本文将连续密度用符号μ(·)表示,表示对所有变量的digamma函数(值取平均值。因此带入H(X)的公式可得:
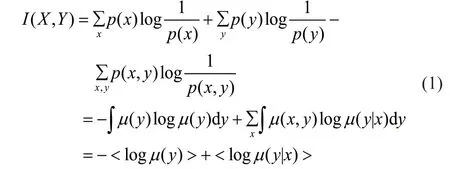
本文参照KRASKOV[14]的k-近邻熵估计法来估计给定数据点的分布。以样本点i为中心点,定义V为在数值上等于比样本i的第k近邻点距离样本更近的样本的数目。熵估计器使用贝叶斯参数,利用来最终确定将样本点i的整个邻域密度函数μ近似为常数,得到:
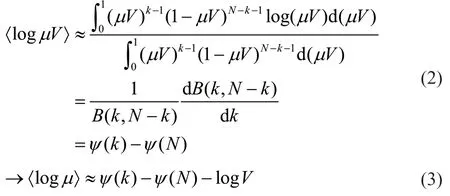
式中,k为距离样本点为μ的样本数目;N为样本的总数;B(·)为Beta函数;ψ(·)为digamma函数;σ(·)表示概率密度函数。
对任意实数P,Q>0:

式中,t表示digamma函数分子的积分变量;为被积表达式。
最终互信息的估计值为:
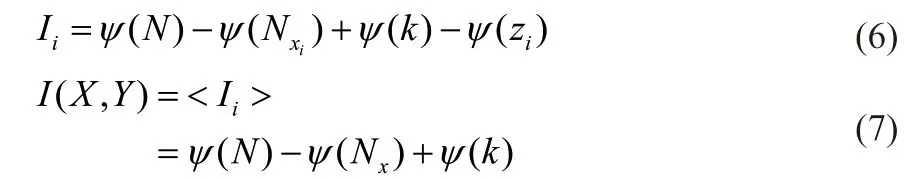
式中,定义d为第i个样本点xi到其对应的特征下第k个近邻样本点的距离; 表示与样本点xi之间距离小于d的样本的个数;zi表示在整个数据集中样本点与xi距离小于d的样本点的个数;Ii表示第i个样本点xi的互信息估计值。
为防止预测模型过拟合,本文采用的基模型为分类决策树(Classification and regression tree,CART),并以二叉树中每一个特征对应分裂结点的泊松偏差(Poisson deviance)与样本加权值的乘积F作为权值系数,进行特征贡献度的筛选。
输入训练前的石油数据集,递归地将每个区域划分为两个子区域,并确定每个子区域的输出值,构建CART,记t,s为每一块区域上的隔离特征与隔离点,通过遍历所有特征,求解下列式子,选择最优的t,s。最终将输入石油数据空间划分为M个区域,生成CART。

令根据特征m划分的区域Rm所在的分裂节点对应的泊松偏差为H(Rm):
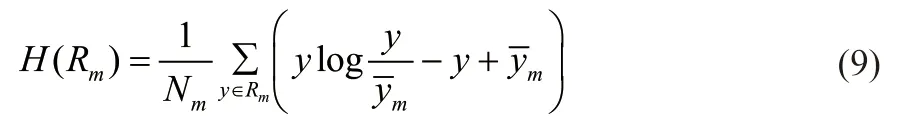

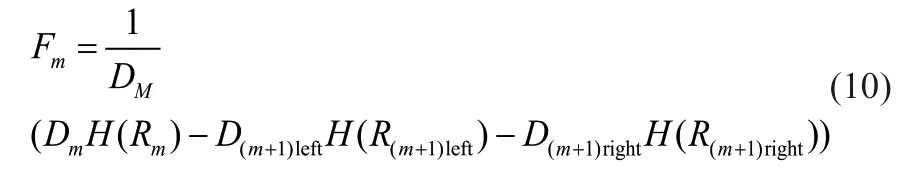
取ξ和ε为融合系数,创立Gm函数为综合评价特征m的重要度的函数,其中z表示样本点与x距离小于d的样本点的个数:
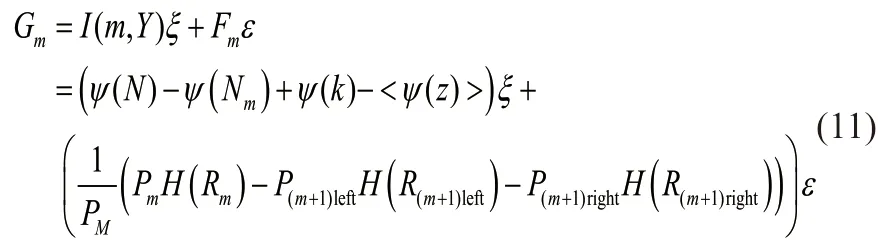
融合系数ξ和ε分别决定了互信息法和CART判据对数据筛选的权重。ξ的数值过小可能会使模型过拟合,在实际预测中误差偏大;ε的数值过小可能会导致冗余特征残留,不利于模型拟合。融合系数的具体取值和数据集本身性质相关,应根据实际数据灵活决定。
1.2 集成学习算法预测
集成学习的思想是将原数据集进行抽样,生成多个新的训练集,并基于新的训练集建立多个基学习器来完成预测任务[16]。相比于单独的算法,集成学习会综合多个基学习器的结果来提高预测精度,并控制模型的过拟合,从而获得更好的预测表现。
对于回归预测,装袋法随机森林的主要流程是:将石油数据集通过Bootstrap有放回抽样后分出多个子数据集,基于子数据集建立多个CART,将所有决策树的预测结果取平均值作为最终的预测结果。对应的步骤如图1所示。
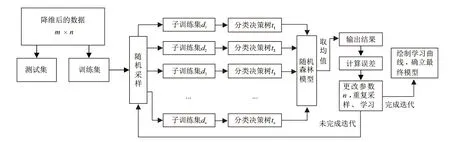
图1 集成学习流程Fig. 1 Ensemble learning process
2 数据预处理
2.1 数据来源
本文数据来源于中国某企业石油加工厂汽油裂解过程中,从2016年初到2019年末期间连续4年的数据记录(以下统称“原数据”)。原数据涵盖了7个原料性质、两个待生吸附剂性质、两个再生吸附剂性质、两个产品性质等变量以及另外354个操作变量(共计367个变量)。为进一步对原数据进行描述,表1展示了原数据中前20个数据特征的信息。

表1 原数据中部分特征指标Table 1 Feature indicators in original dataset
2.2 数据预处理方法
数据预处理是指从原数据中检测并纠正、修复存在粗大误差的数据的过程。传统的数据预处理过程采用平均值填充、众数填充等方法对数据进行纠错处理[15-16],本文根据现有数据集的特点(高维、高噪声和奇异值含量高),将数据集的预处理环节分为缺失值检查、方差过滤、最大占比过滤和基于三西格玛准则的奇异值过滤4个部分。预处理环节的流程图如图2所示。
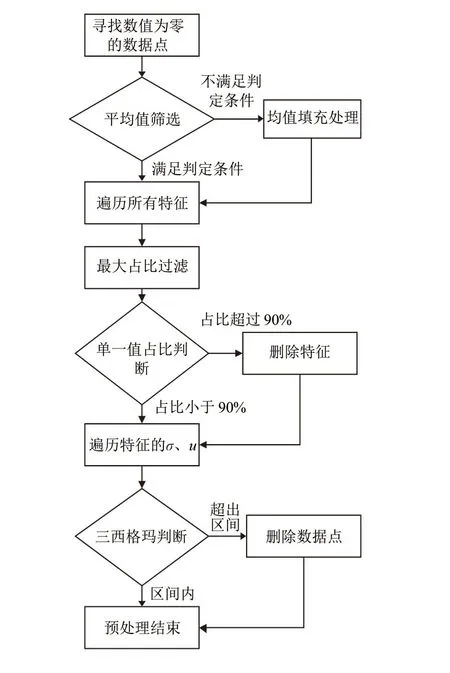
图2 预处理环节流程Fig. 2 Preprocessing process
预处理环节中主要涉及以下步骤:
(1)缺失值检查。先将数据中含有零的数据项提取出来,并将该特征的所有样本点进行取平均值处理,若满足证明该点位存在数据缺失问题,需要对该特征进行补充或删除处理。其中,α和ω是均值和标准差所占权重,为该特征下所有样本的平均值。根据实际经验,以及查阅相关文献[17],本文α和ω均设置为0.5,c通常设置为100[17]。
(2)方差过滤。过滤掉方差较小的特征。在做辛烷值损失预测时,方差较小的特征对预测的贡献度也相应较小。
(3)最大占比过滤。若某一特征中一个数值占比很高,这类特征对数据预测的贡献度很低,例如,“进料调节阀旁路流量”中有307个一样的数据,对类似的数据进行删除。
(4)基于三西格玛准则的奇异值过滤。三西格玛准则是一种常用的去除一组数据中粗大误差值的方法:
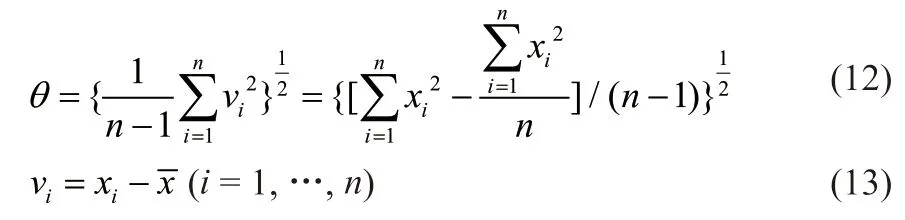
式中,θ为标准误差;vi为剩余误差。
对原数据进行上述步骤的预处理,数据处理前后的维度变化如表2所示。

表2 数据集预处理前后维度对比Table 2 Dimensional comparison between unprocessed and processed data
3 汽油中辛烷值预测的模型应用和结果分析
3.1 模型应用
成品汽油中,辛烷值的传统化工建模过程一般是通过物理数据匹配和化学机理实验来完成的[13],该过程需要采集的化学数据种类繁多,且对化学原料的分析要求很高[6]。在实际工厂加工过程中,要在一段加氢脱硫单元与二段加氢脱硫单元的加工间隙中测定烯氢和芳氢的含量,采集过程如图3所示。
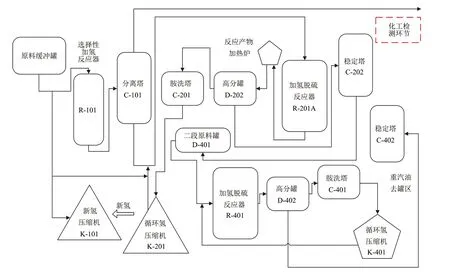
图3 辛烷值化工检测流程Fig. 3 Chemical process obtaining octane value
本文的数据提取环节仅需从操作点位获取相关流量、温度和原料性质等信息,基于历史数据进行建模分析、模式提取,并在汽油裂解过程中通过实时辛烷预测值及时优化相关操作位点[19],在成品汽油产出前把控其品质,达到效率、利润最大化。相比于传统化学方法,其安全性与准确性更高,更利于工厂的实际应用。
3.2 计算结果分析
3.2.1 融合评价效果分析
在数据融合降维处理过程中依照便于工程观察的原则[20],选取Gm函数值排在前30的特征作为训练的样本,即数据维度从原始的290个特征降至30个特征,达到了数据降维的目的。其中Gm函数值排名前30的特征柱状图如图4所示。横坐标为特征的名称,纵坐标为函数对应的数值,绿色柱状图为互信息法的估计值,橙色柱状图为CART特征重要度。由图4可知,不同特征按照本文提出的融合算法评价方法计算出的融合评价数值存在差异,数值越小表明对模型预测精度的贡献度相应地减少。其中,特征“P-101B入口过滤器压差”对模型的预测精度贡献度最高,特征“D-107温度”在290个特征中排名为第30,完成了对数据降维处理。
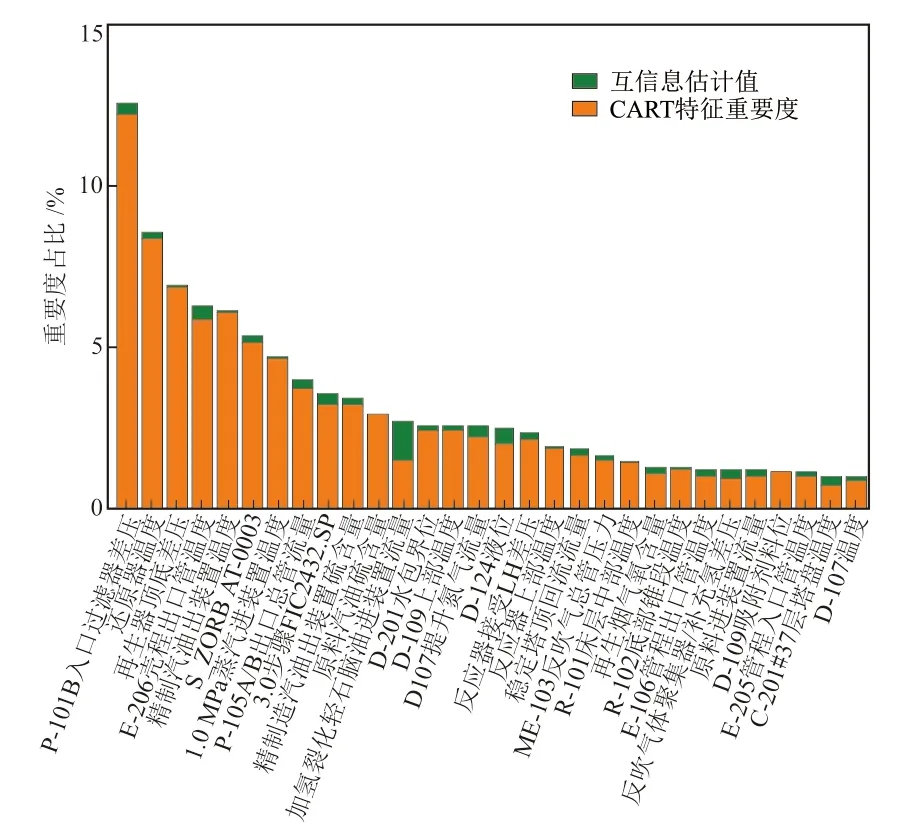
图4 融合算法评价指标Fig. 4 Fusion algorithm evaluation index
3.2.2 模型评价指标与模型学习曲线
本文以数据预处理后的91350个样本按照7:3的比例划分为训练集和测试集。为了验证本文提出模型的有效性,本研究中采用均方误差(MSE)、均方根误差(RMSE)、均方对数误差(MSLE)、最大误差(Max Error)、最小误差(Min Error)、回归平方和(ESS)以及残差平方和(RSS)作为评价函数,对预测的结果进行分析比较。
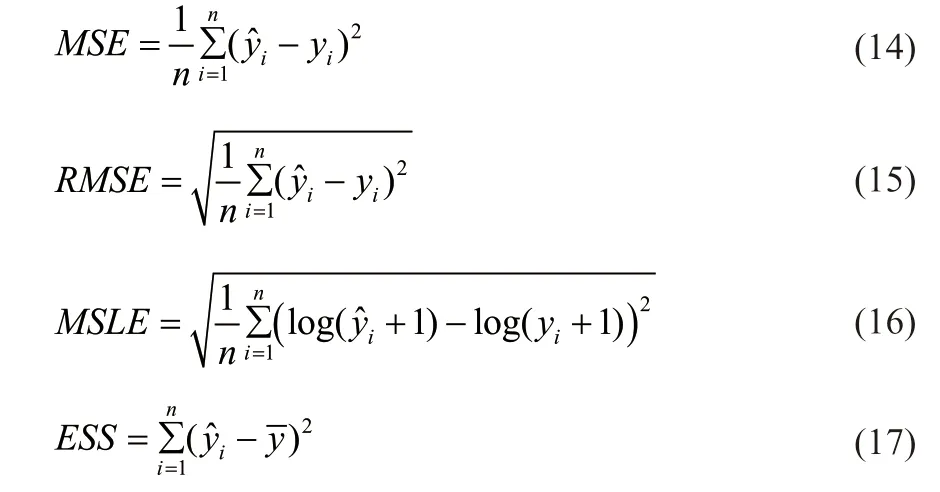

式中,n为测试集样本个数,为模型基于测试集中第i个数据的辛烷值损失量的预测值;yi表示第i个数据在测试集中的实际辛烷值损失量为测试集样本的辛烷值损失量的平均值。
当预测值相对于实际值误差较为明显时,MSE的实用性更高,能够很直观地比较模型之间的预测效果,但如果测试样本的预测误差之间有很大的差异,MSE作为评价函数可能会被数值大的误差所引导,MSLE对样本数据取对数后再求标准差,这种取值方式能够缓解误差过大的问题,对模型的准确度有更客观的评价。
在集成学习模型训练过程,为使得模型获得最佳的学习效果,本文基于不同CART的数量进行了多次对比,学习曲线如图5所示。由图5可知,随着回归树数目的增加,模型的误差在一定范围内不断减少,最终趋于平衡,这表明回归树的数量直接影响模型的预测精度。最终选择基学习器数量为90的集成学习模型作为本研究的预测模型。
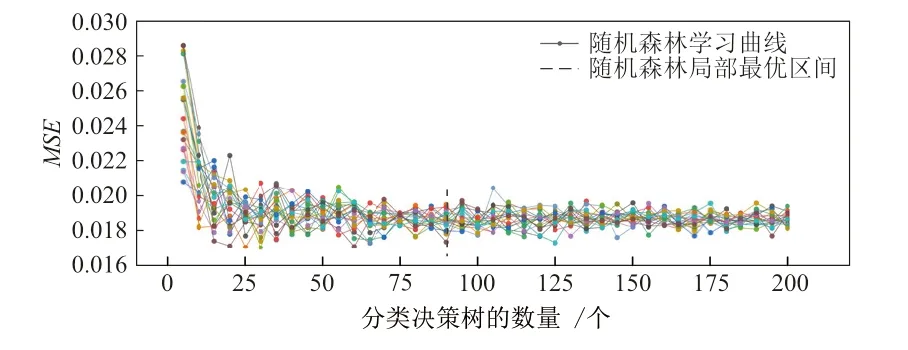
图5 随机森林关于参数的学习曲线Fig. 5 Random forest learning curve based on parameters adjustment
3.2.3 融合降维算法有效性验证
由于前人的降维算法和预测算法存在数据上的脱节,不具有流程上的连贯性,降维会损失原始数据集的部分信息,预测结果并不理想。本研究考虑到降维和预测之间的联系[20],利用融合算法在尽可能减少数据信息损失的前提下,减少数据集的冗余,保证了降维后的预测精度不受维度的影响,对比结果如表3所示。
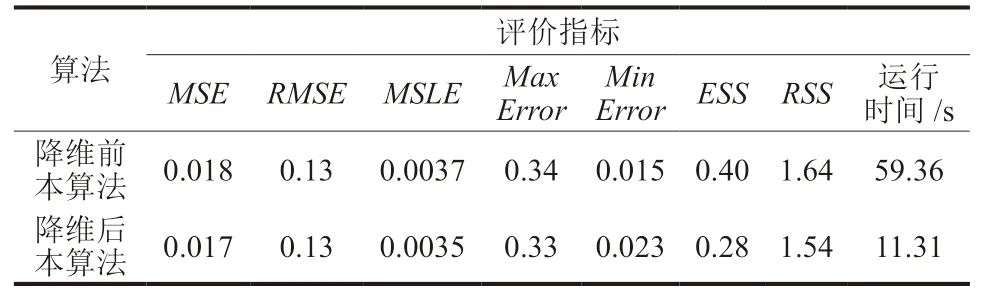
表3 石油数据集降维前后结果对比Table 3 Comparison of errors between original data and dimension-reduced data
降维前的石油数据集有290个特征,降维后的特征数减少至30个,较原始数据集减少了89.65%。由于融合算法减少了数据集中的冗余数据,保证了在测试集中检测精度相比原数据集不降反升,MSE、ESS和RMSE分 别 减 少 了6.45%、29.33%和3.28%。但在Min Error这一评价指标上没有原始数据集表现优越,原始数据集的信息量更大,在某些特征上的学习相对降维后的数据集更为充分,因而Min Error较小。运行时间上,降维后的数据集训练的时间减少了约81.43%,原始数据集的运行时间是降维后的5倍多,因此相比于直接对原始数据进行处理的方法,融合降维预测的数据处理框架的计算效率是更高的。
3.3 不同模型的对比分析
3.3.1 融合降维算法与传统降维算法的比较
本文按照文献[8]中的PCA降维算法、文献[15]中的k-近邻降维算法以及本文提出的MIR-EFS融合降维算法分别对原数据进行了降维处理,并采取控制变量的方法,用相同的预测方法(集成学习随机森林模型)对石油数据进行训练和预测,结果的对比见表4。

表4 不同降维算法的预测结果Table 4 Prediction results of different dimensionality reduction algorithms
从表4中可以看出,本文提出的融合降维算法的MSE较文献[8]中PCA降维算法和文献[15]中k-近邻降维算法分别降低了约34.20%和26.08%,运行时间减少了39.26%和44.88%。综合各类评价指标,本文融合算法的各项误差均小于文献[8]中的PCA降维算法,且PCA降维算法改变数据维度的同时,破坏了数据的物理意义,创建的新特征无法在实际工程中检测,而融合算法筛选后的特征便于工程监测,有更高的物理解释性。
3.3.2 MIR-EFS融合降维算法与传统预测算法的比较
为进一步验证传统预测算法和本文提出的MIR-EFS融合降维算法之间的差别,本研究采用多种模型对辛烷值进行了预测,表5给出了7类不同模型的预测精度、训练时间的结果,各类模型预测值和真实值的对比曲线如图6所示。

表5 不同预测模型的对比Table 5 Comparison of different prediction models
由表5可知,本文模型的MSE相比于决策树模型、文献[9]采用的XgBoost模型分别减少了43.3%和17.6%;本文模型在训练时间上的消耗略高于一些基础的模型,例如文献[6]采用的主成分Lasso回归和决策树等。但相比于一些稍复杂模型,如文献[9]中经过PCA降维后的XgBoost模型、SVM-Poly模型,本文模型训练花费的时间又相对较少。由此可见,MIR-EFS集成学习模型在预测精度和时间消耗上有着较好的平衡,在保证预测精度的同时,尽可能地提升了计算的效率。
由图6可知,经MIR-ESF融合降维算法处理过后的数据经过集成模型预测出的结果和样本测试集中真实值的拟合度较高,无论是数据分布或极值范围都较大程度地预测出辛烷值的数据特征。在训练集中有6个点位误差值为0,96.3%的数据误差在0.2以内,数据的预测精度较高,证明了本文模型有着良好的辛烷值预测能力。方法1曲线为文献[9]中经过PCA降维后的XgBoost模型预测结果;方法2曲线为文献[6]的k-近邻降维算法预测结果。从3个虚线对实线的拟合程度可以看出,与文献[6]中提出的主成分Lasso降维算法和文献[9]中经过PCA降维后的XgBoost模型相比,本文提出的MIR-EFS融合降维算法对数据的拟合程度更高,误差更小。在测试集的特定点位上,文献[6]与文献[9]的模型与本文模型做出具有相似趋势的预测,但由于XgBoost模型和Lasso模型在辛烷值预测问题上具有过拟合、数据脱节的束缚,使得数据误差较高,无法生成高精度的预测结果。
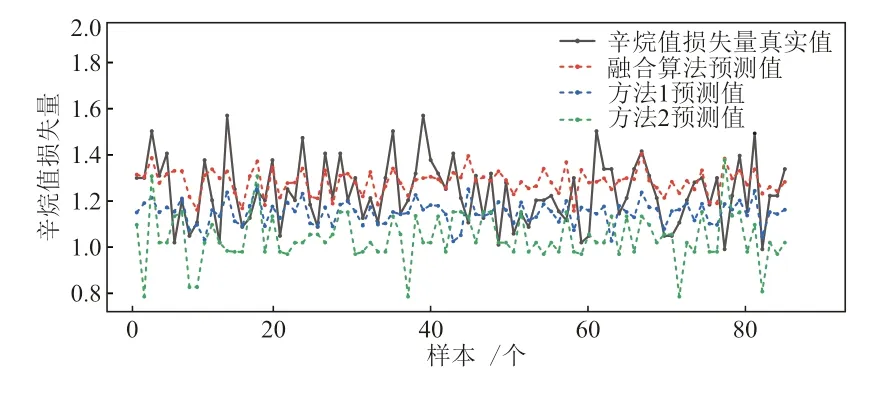
图6 MIR-EFS融合算法与文献中方法的对比Fig. 6 Comparison between MIR-EFS fusion algorithm and other algorithm
4 结论
本文以某加工厂石油裂化过程中各类操作节点的历史数值作为数据来源,提出了一种MIREFS融合降维算法,并基于自适应的随机森林集成学习算法建立了辛烷值预测模型,最终得出如下结论:
(1)MIR-EFS融合降维算法充分利用了数据的多重性质,多维度地考察了数据的特性,保留了特征的物理特性,且降维后仍保持了预测的准确性。
(2)MIR-EFS融合降维算法框架将数据维度减少了89.65%,训练时间减少了81.43%,MSE误差降低至0.017,各项检测指标均高于传统预测模型。
(3)由于在建模过程中考虑到了降维和预测部分数据的连贯性,本研究建立的自适应集成学习随机森林模型和XgBoost模型、Lasso模型、单一决策树模型相比有着更低的预测误差以及更高的鲁棒性,本研究建立的模型的MSE、RMSE、Min Error和ESS分别为0.017、0.13、0.023和0.28。
本文提出的算法框架解决了辛烷值原本难以获取的工程问题,更适合于辛烷值预测的实际工程应用,为同类技术提供了可参考的算法支持。

