一种改进后的尾桨叶安装角测量方法

耿丽松，杨茜茜，焦帅克，王泽峰

（1.中国飞行试验研究院飞机所，陕西 西安 710089；2.中国飞行试验研究院测试所，陕西 西安 710089）

在直升机尾桨叶设计阶段，为了使气动力沿桨叶展向相对均匀分布，不同径向位置处的安装角会设计成负扭转分布，一般桨根处的安装角大于桨尖处的安装角。尾桨叶在旋转过程中，存在挥舞运动和摆振运动[1-3]，桨叶各剖面不同安装角的设计特点就导致在桨叶旋转时，挥舞运动和摆振运动必然存在耦合，即挥舞方向的受载情况会影响摆振方向的应变输出，摆振方向的受载情况同样会影响挥舞方向的应变输出。

对挥舞和摆振的耦合运动进行解耦是飞行载荷测量中的重要环节，这一环节在地面载荷标定试验中完成。简单来讲，挥舞-摆振解耦的物理方法即为在垂直于某一剖面弦线和平行于该弦线的方向上分别进行静态加载，以获得该剖面纯粹的挥舞弯矩、摆振弯矩与挥舞响应、摆振响应的关系。对于形状规则的一般结构件或者固定翼飞机的平直机翼而言，载荷标定试验较为简单，逐级加载和记录各级输出即可。而由于直升机桨叶各剖面弦线不在同一平面的这一特殊性，在进行桨叶挥舞-摆振载荷标定之前，确定桨叶各剖面的安装角则是必须完成的第一步。

目前在国内外工程实践中，通常采用应变计法进行飞行载荷测量，在飞行实测前需对尾桨叶进行载荷标定。试验中寻找各剖面安装角的一般做法[4-5]是，桨叶根部固定，尖端在摆振方向施加一定载荷，不断调整桨叶固定端角度，记录各剖面挥舞方向应变片的输出值，得到挥舞应变输出随调整角度的变化关系，当某一剖面挥舞应变输出为零时，我们认为此时对应的角度即为该剖面的安装角。这种物理解耦的方法较为成熟，已广泛应用于我国各类直升机型号任务中[6]。

但是，在某型直升机地面载荷标定试验中，发现使用该方法进行安装角测量时，重复性并不太好，得到的结果与桨叶固定时的初始角度有较大的关系，试验初始角度改变，结果便发生变化。

本文首先介绍寻找桨叶安装角的传统工程方法，通过实例指出其中存在的缺陷；从理论层面分析了这种缺陷的来源和造成的影响，并给出数据修正办法和此类试验的改进建议；最后以某型直升机尾桨叶寻找安装角的工程实践为例，证明了该改进方法的准确性。

1 确定尾桨叶安装角的传统方法

以往的工程手段通常是在一定范围内多次调整尾桨叶固定端角度，测量摆振方向加载时挥舞应变计的输出，由此得到挥舞方向应变输出为零时的摆振加载角度，该角度即为该剖面的安装角。

根据经典薄翼型理论[7]，桨叶或机翼受气动载荷时，翼型压力中心大致位于距离前缘的1/4弦线处，所以测量尾桨叶挥舞弯矩的电阻应变计一般贴在各剖面上下翼面的距离前缘1/4弦线位置[8]，上下翼面各贴一组平行应变片，组成全桥电路[9]，如图1和图2所示。

图1 挥舞应变计贴片位置示意图

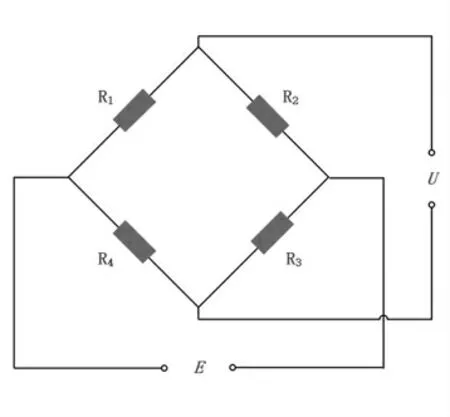
图2 全桥电路示意图

桥路输出电压U与激励电压E关系如式（1）所示。

其中，k为应变计灵敏度系数，ε为桨叶剖面挥舞应变值。

将尾桨叶桨根处固支，桨尖处加载，调整至竖直位置，使弦线与竖直方向（即摆振加载方向）呈一定初始角度β0。在一定范围内调整尾桨叶固定角度β，如图3和图4所示。记录在不同角度摆振方向加载时，对应的挥舞方向应变输出X，绘制角度β和挥舞输出X的拟合关系曲线，得到线性关系式如式（2）所示。由此，即可得到挥舞输出X为0时的摆振加载角度β，即为所要求的该剖面安装角。

图3 摆振加载方向示意图

图4 加载剖面示意图

这里以某型直升机尾桨叶剖面r1和r2为例说明该类试验的缺陷，使用这种方法进行尾桨叶的安装角测量。

第一次试验时，调整尾桨叶从初始角度0°到终止角度10°，得到各角度下的挥舞应变输出值如图5所示，令两个剖面挥舞输出值X等于0，可得出剖面r1和r2安装角分别为-8.091°和-6.286°。

图5 各剖面挥舞输出与调整角度关系

为了确保试验有较好的重复性，又反向调整尾桨叶角度进行第二次试验，即调整尾桨叶从初始角度10°到终止角度0°，得到的结果如图6所示，令两个剖面挥舞输出值X等于0，可得出剖面r1和r2安装角分别为-3.299°和-2.449°。这个结果与第一次试验有明显的不一致性。

图6 各剖面挥舞输出与调整角度关系

两次试验仅仅是改变了角度的调整顺序，便得到了不一致的结果，说明试验方法本身是存在问题的。特定剖面的安装角应当是一个定值，不应随试验流程的不同发生改变。

经过多次试验确认，发现得到的安装角结果确实与尾桨叶固定在工装夹具上的初始角度有关，若初始角度选取不同，得到的结果就是不同的，并且结果的差异性呈现出两个特点：（1）调整角度的范围越大，这种差异性就越大；（2）剖面越靠近尾桨叶根部，这种差异性也越明显。

2 改进方法的理论基础

针对传统方法中遇到的问题，进行了一系列猜想与验证，最终发现：调整的角度不同，则尾桨叶自由端的重力在挥舞方向的分量不同，这将直接影响到挥舞方向应变的输出。

如图7所示，坐标系X0OY0为尾桨叶0剖面的平面坐标系，坐标系XOY为标定剖面的平面坐标系，坐标系XGOYG为标定剖面外端部分的重心所在剖面的平面坐标系，坐标系XFOYF为加载平面坐标系。

图7 各坐标系示意图

若初始角度为β0，此时标定剖面实际的挥舞应变X0s应为：

其中，K为标定剖面的比例常数，F为加载力大小，LF为加载力对标定剖面的加载力臂，β0为标定剖面与尾桨叶0剖面的初始夹角，βF为加载力剖面与尾桨叶0剖面夹角，βG为标定剖面外端部分的重心所在剖面与尾桨叶0剖面夹角，LG为重力对标定剖面的力臂。

在连接且检查好测试设备后，通常做法是在空载状态先记录一个初始值，再进行加载，加载后的应变计输出值减去初始值，即为初始角度β0时的应变计输出，此时相当于清除了β0位置时重力对结果的影响，即输出值X0应为：

随后转动角度至β，此时实际的挥舞应变Xβs为：

而输出值Xβ为：

当角度较小时，上式也可以写成：

尾桨叶标定试验期望得到的是加载力与各剖面应变响应的关系，即（7）式中的第一项，而第二项是重力带来的影响，是不希望掺杂进去的部分。实际试验中，转动角度通常在0°~10°之间变化，则对于初始角度为0°，整个试验过程重力带来的影响大致为：

则最大误差为10°位置，为0.174 G*LG。

对于初始角度为10°，整个试验过程重力带来的影响大致为：

则最大误差为0°位置，为-0.174 G*LG。

于是，便出现了从0°向10°转动和从10°向0°转动这两种试验流程会产生不一致的结果，且这种影响是不可忽略的。

当β和β0越接近，即转动角度的变化范围越小时，重力对结果的影响越小；同时，越靠近桨尖的标定剖面，其外端尾桨叶质量越小，则重力对结果的影响也就越小。

3 基于实例的误差修正和改进方法

针对上述提到的相关问题，提出了对已有试验数据的一种修正办法和对于此类试验的改进建议。

3.1 对已有数据的修正

使用传统试验方法，已得到了从0°向10°转动和从10°向0°转动这两种试验流程产生的两组结果，将β0＝0°和β0＝10°分别代入式（7），即可得到任意角度β时的两种输出结果。

初始角度为0°：

初始角度为10°：

式（10）减去式（11），即可得到10°位置和0°位置的重力对输出结果影响的差值。

由此可见，对于特定剖面，式（12）为一定值。在小角度范围内，可假设重力的影响在0°到10°范围内线性变化，则通过线性插值，即可得到任意角度位置重力对输出结果的影响△Xβ_β-0或△Xβ_β-10。

将任意角度重力的影响代入式（10）或式（11），即得到加载力与各剖面应变响应的关系式（15），通过拟合得到各剖面预扭角。

仍然以某型直升机尾桨叶r1剖面和r2剖面的实例来说明上述改进方法。

试验采用的是CAM500数据采集器，激励电压为5 V，采集器以码值形式输出，可直接转换为应变值。

电阻应变计贴在r1剖面和r2剖面上下翼面距离前缘1/4弦线位置，在摆振方向0°到10°范围加载，加载力恒为100 N。

按照上文提到的传统方法进行试验，得到初始角度为0°和初始角度为10°时的两组数据式（10）和式（11），两式相减得到10°位置和0°位置的重力对输出结果影响的差值，见表1和表2。

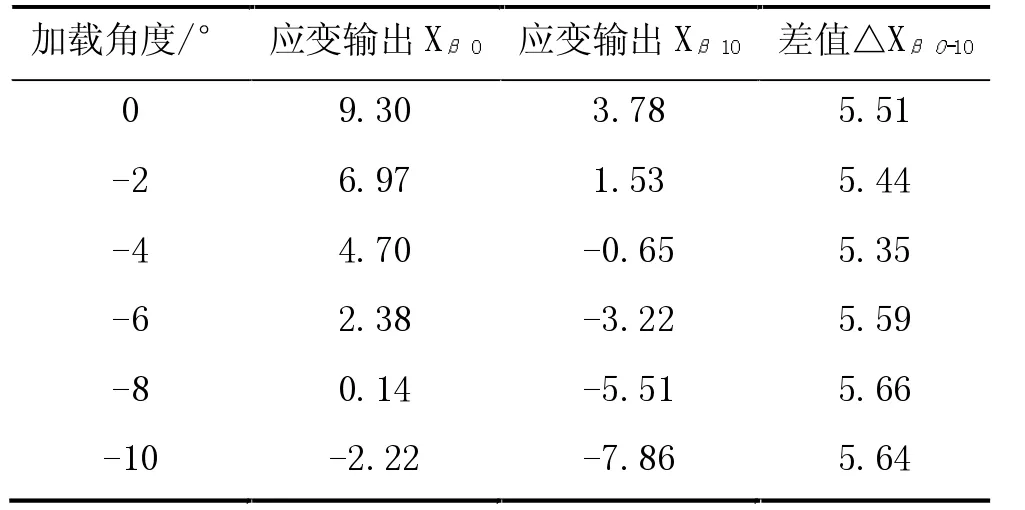
表1 初始角度不同时所对应的r1剖面应变输出值

表2 初始角度不同时所对应的r2剖面应变输出值

可以发现，在相同的加载角度，两个不同的初始角度对应的两组数据相差较大，这说明选择不同的初始角度会明显影响到应变输出结果，继而影响到后续安装角的计算，因此采用上述改进方法对试验数据进行修正是很有必要的。

同时，同一加载角度下两组数据的差值几乎是相等的，这表明式（12）是个恒定值，与上述理论分析是吻合的，证明了上述改进方法的正确性。

取r1剖面两组数据差值的平均值为：

代入式（13）或式（14），通过线性插值，得到任意加载角度β时重力对r1剖面挥舞输出的影响：

使用式（10）和式（11）对原始数据加以修正，得到加载角度与r1剖面挥舞应变输出修正值关系，见表3。

表3 初始角度不同时所对应的r1剖面挥舞应变输出修正值

同理，可得到任意加载角度β时重力对r2剖面挥舞输出的影响：

加载角度与r2剖面挥舞应变输出修正值的关系见表4。

不难发现，不同初始角度所对应的挥舞应变输出，经过修正后具有很高的重复性。从修正后的表3和表4中各选出一组数据，拟合出加载角度与各剖面挥舞应变输出值的线性关系，如图8所示，得到挥舞应变零输出时的加载位置，即得到对应剖面的安装角。

图8 各剖面挥舞输出与调整角度关系

表4 初始角度不同时所对应的r2剖面挥舞应变输出修正值

图中，用R2来衡量回归方程整体的线性拟合度，表达因变量与自变量之间的总体关系，其值等于回归平方和在总平方和中所占的比率，范围为0~1，R2越接近1，则表示线性拟合度越好。

令应变输出X等于0，可得对应的加载角度为-5.459°和-4.497°，即r1剖面和r2剖面的安装角分别为-5.459°和-4.497°。

设计给出的r1剖面和r2剖面安装角分别为-5.94°和-4.82°，即可计算出通过该方法得到的结果相对误差为：

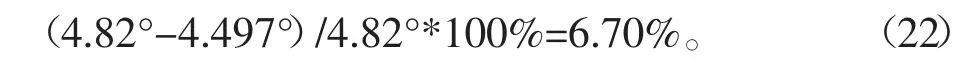
满足工程要求，由此证明了该修正方法的有效性和准确性。

3.2 后续试验的改进建议和验证

前文已详细阐述了基于原始实测数据的修正办法，实际上，在今后的预扭角试验中，可以通过调整试验方法，消除寻找安装角时的重力影响，直接得到加载角度与挥舞应变输出的关系。

上述问题存在的原因主要在于初始角度选取不同而带来的差异，之后的试验中，可以考虑在每次转动尾桨叶加载角度后，重新记一次零位，然后再进行加载。即在每一个加载角度，都只得到加载力对应变的输出值，而消除掉重力的因素，通过这种方式得到的安装角和挥摆载荷-应变校线，在之后的飞行试验中，解算出的结果可认为是纯气动力带来的影响，而不是气动力与重力共同作用的结果。

在分析清楚上述问题并给出试验改进建议后，进行了验证试验，即在每次加载后清除重力影响，得到数据见表5，拟合曲线如图9所示。

表5 试验改进后的应变输出值

从图9可知，采用改进建议后的试验数据线性拟合度较高，得到r1剖面和r2剖面安装角为-5.506°和-4.529°，与设计值相比较，可知相对误差为：

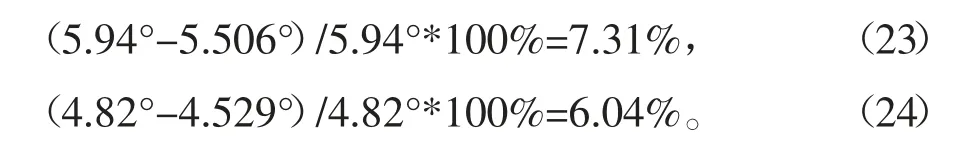
图9 试验改进后应变-加载角度拟合关系

从图表也可看出，改进试验的数据结果与3.1节提出的数据修正办法得到的结果非常吻合，且与设计值均比较接近，这便验证了本文改进方法的准确性。本文改进方法的研究思路也为同类型试验的排故提供了参考方向。

4 结论

（1）对于确定尾桨叶各剖面安装角的传统工程方法，指出其中存在的缺陷为忽略了重力影响，从理论层面分析了误差来源，且通过实例证明了重力影响带来的这种误差是不可忽视的。

（2）给出传统方法缺陷的两种修正思路，以某型直升机尾桨叶为例，改进并完成了寻找尾桨叶安装角的工程实践，证明了改进方法的有效性和正确性，此改进方法在工程上已得到应用和验证。