静电场作用下单相电介质系统的热力学特征
韩光泽 邢雨锟 胡秋霞 陈俊岩
(华南理工大学 物理与光电学院,广东 广州 510640)
由于具有高效性、可控性和易操作等优点,电场被越来越多地应用于工业生产和制造过程当中。将电场技术应用于生产过程,可以缩短生产时间、提高生产效率和产率、节约能源和投资成本、保护环境等。与电场相关技术的开发和应用是近年来的一大研究热点。但相关的应用还非常有限,虽然吸引了广大学者的关注,但有关的研究还主要是以探索性的实验为主。例如,在国内的学者中,熊宇飞等[1]实验研究了高压静电场结合制冷对刀额新对虾的保鲜作用,发现施加高压静电场结合冷冻能够延长保鲜期2天以上;尹浩然等[2]实验研究了直流电场作用下油中异性水滴聚并特征,发现直流电场对异性水滴间液桥的对称性有较大的影响;王东保等[3]实验研究了电场强化酯交换过程中醇油两相分散的特性,发现电场能够强化相间传质和相分散;郭磊等[4]实验研究发现电场能够强化微槽道结构毛细芯蒸发器的传热过程;王祖武等[5]研究发现放电电场能够强化SO2气相传质过程。国际上也有一些学者开展了相关的实验研究,Kazuhiko等[6]实验发现强电场可以引起过冷乙醇气体在电极周围成雾;有些学者[7- 8]较详细地实验研究了电场对传热和传质过程的强化作用。这些实验研究都表明,电场能够显著地改变系统的状态,对相关过程的进行有一定的调控作用。
由于理论研究的不足,实验研究和应用技术开发缺乏理论指导,在电场技术的应用方面还远不尽人意。近年来韩光泽等[9- 12]运用热力学理论,对电场作用下电介质系统的特征开展了较详细的理论探讨,取得了一定的研究成果。提出了电场作用下化学势的普遍化表达式,揭示了电场作用引起气液两相系统相变过程的热力学机理[13- 15]。本文中将在前面研究工作的基础上,较详细地探讨在均匀静电场作用下单相电介质系统的热力学行为。
1 静电场作用下的单相电介质系统
1.1 单组分气体电介质系统
如图1所示,设有一个带电平行板电容器置于单相电介质系统中。忽略边缘效应,电容器内有电场强度为E的均匀电场。该系统包括电容器内部和外部两部分,化学组成相同的流体电介质充满系统整个空间。设电容器两个极板之间的空间占整个系统空间的比率很小,即电容器的置入对整个系统的性质没有影响。当系统达到热力学平衡时,电容器内电介质的物理性质与电容器外系统其它部分电介质物理性质的差异就是静电场的作用效果。下面分单组分气体、单组分液体、多组分气体和多组分液体4种情况讨论。
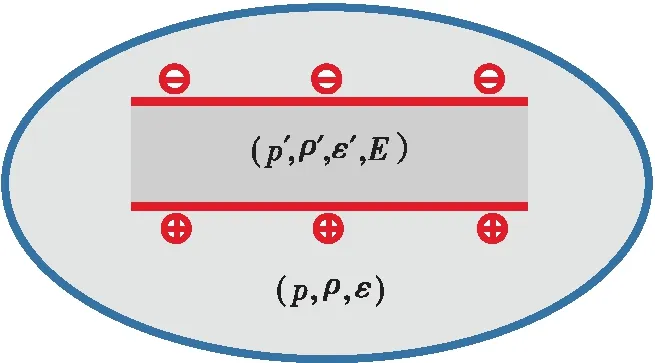
图1 电介质系统内的带电平行板电容器
首先,设该系统是由单组分理想气体组成,下面计算电容器内外电介质的压强和密度关系。由Gibbs-Duhem方程SdT-Vdp+ndμ=0得等温下的化学势dμ=vdp,v为摩尔体积,μ为化学势,S为熵,T为热力学温度,V为体积,p为系统压强。由理想气体方程pv=RT积分得纯气体的化学势[15- 16]。
μ(T,p)=μ(T,pθ)+RTln(p/pθ)
(1)
式中,R是摩尔气体常数,pθ是初始阶段系统压强。在前面的工作中已经导出了电场作用下电介质组分的化学势[13- 14]。
(2)
式中:ε0、ε分别为真空中的介电常数和介质的相对介电常数;Mi为摩尔质量;下标i表示组分;ερ≡∂ε/∂ρ;ρ为密度;E为电场强度;文中的上标“′”表示电场作用下的物理量。对于流体电介质,利用Clausius-Mossotti式[17]可得
ρ∂ε/∂ρ=(ε-1)(ε+2)/3。
由热力学平衡中的相平衡条件可知[16],当系统处于平衡状态时,介质组分的化学势在整个系统应该是均匀单一的,即电容器内外介质组分的化学势应该相等,
μi(内)=μi(外)
(3)
式(3)具有普遍意义,适用于任意组成、任意状态的电介质系统。利用式(1)和式(2)可将这个相平衡条件式(3)具体表达为
μ(T,pθ)+RTln(p/pθ)
(4)
由式(4)可得静电场作用下电容器内外气体的压强关系
(5)
式(5)表明,压强的变化与场强的平方成正比,与温度成反比。由理想气体方程得p′/p=ρ′/ρ,也就是说气体的密度与压强具有相同的变化关系,即ln(ρ′/ρ)=ε0ερME2/(2RT)。
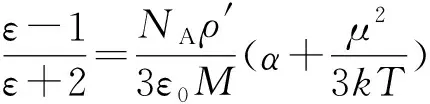
(6)
式(6)与文献[18]的结论一致,但文献[18]在导出该式的过程中使用的化学势与电容器的体积有关,这显然是不符合逻辑的。系统中物质组分的化学势是一个强度参量,应该只决定于温度和压强以及电场强度等,不可能与系统的体积有关[16]。
1.2 单组分液体电介质系统
设图1所示的系统是由单组分液体电介质组成,下面计算电容器内外的压强差。液体的摩尔体积v随压强变化很小,由化学势的微分dμ=vdp积分得纯液体的化学势[16]
μ(T,p)=μ(T,pθ)+v(p-pθ)
(7)
将式(2)和式(7)带入相平衡条件式(3)得
μ(T,pθ)+v(p-pθ)
(8)
由式(8)可得静电场作用下液体电介质系统的压强变化
(9)
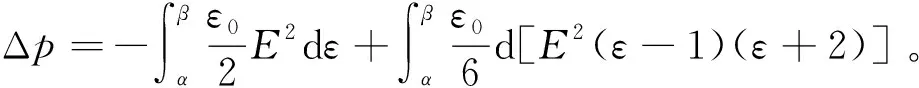
1.3 多组分气体混合物电介质系统
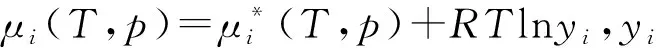
(10)
利用纯气体化学势式(1)可将式(10)改写为
(11)
Landau等[19]学者讨论了流体电介质在电场作用下的介电力,讨论过程并未区分纯物质电介质或混合物电介质,结论具有普遍的意义。也就是说,电场作用下纯物质电介质和混合物电介质具有相同的力学规律。由此可以推断,电场作用下混合物电介质的压强与纯净物电介质的压强具有相同的变化关系。混合物气体的介电常数和摩尔质量分别是ε=∑yiεi和M=∑yiMi,利用混合物的介电常数和摩尔质量将式(5)带入式(11)即得到静电场作用下气体摩尔分数的变化:
(12)
1.4 多组分液体混合物电介质系统
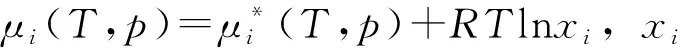
(13)
利用纯液体的化学势式(7)可将上式改写为
(14)
混合液体的介电常数和密度分别是ε=∑xiviεi/∑xivi和ρ=∑xiMi/∑xivi,vi=Mi/ρi,利用式(9)即可从式(14)得到静电场作用下液体混合物电介质的摩尔分数的变化:
(15)
2 讨论
2.1 静电场作用下气体的压强
式(5)或式(6)中的p′表示静电场作用下气体的压强,而p为相同温度下没有静电场时气体的压强。因此该式表明,静电场作用会导致气体的压强上升,上升的幅度与电场强度的平方成正比,与温度成反比。图2是依据式(5)得出的甲醇气体的压强随温度和电场强度的变化曲线图,该图清晰地表示出了静电场作用下甲醇气体的压强随温度和场强的变化趋势。电场强度越大、温度越低,压强变化越明显,但总体变化不大。

图2 甲醇气体的压强随温度和场强的变化
处于某一温度的气体,其压强一般低于该温度下的饱和蒸气压。在温度不变的条件下,如果增加气体的压强使其达到饱和蒸气压,气体将凝结成液体。因此静电场作用导致压强上升将可能引起气体凝结。由Antoine方程可知[20],气体的温度越低,饱和蒸气压也越低。因此气体的温度越低,静电场作用越容易导致凝结发生。一方面温度越低,与该温度对应的饱和蒸气压也越低;另一方面温度越低,电场作用下气体的压强升高也越多,气体的实际压强更易达到饱和蒸气压。电场导致气体凝结现象已被实验所证实。例如,Kazuhiko等[6]观察到强电场可以导致乙醇气体雾化,Zhang等[21]注意到在高寒地区高压直流容易引起空气液化。
2.2 静电场作用下液体的压强
式(9)表明,静电场作用下液体的压强会有所增加。压强的增加量不仅与电场强度的平方成正比,还与介电常数有关。利用这个性质可以设计一个如图3所示的装置,将两块相互平行的带电金属板垂直插入电介质液体中,由于板内的压强高于板外的压强,液体将在板内向上上升一定的高度h。利用力学平衡关系可以计算出这个高度,h=ε0·(εliquid-εgas)E2/(2ρg),g为重力加速度。液体的介电常数随温度上升而减小,这个关系通常可以用经验公式ε=a+bT+cT2+dT3表示[22],其中a、b、c和d为经验常数。从式(9)可以看出,温度越低,压强增加越多,液面也上升的越高。Baptiste等[23]实验测量了带电平行板间液面上升的高度与电场强度及温度的关系,测量结果与本文的结论相符。介电常数是一个重要的物理量,如果已知液面上升的高度,可从这个公式计算液体的介电常数。由于高度是一个容易测量的量,因此这个装置也提供了一种简易的测量液体电介质介电常数的方法。
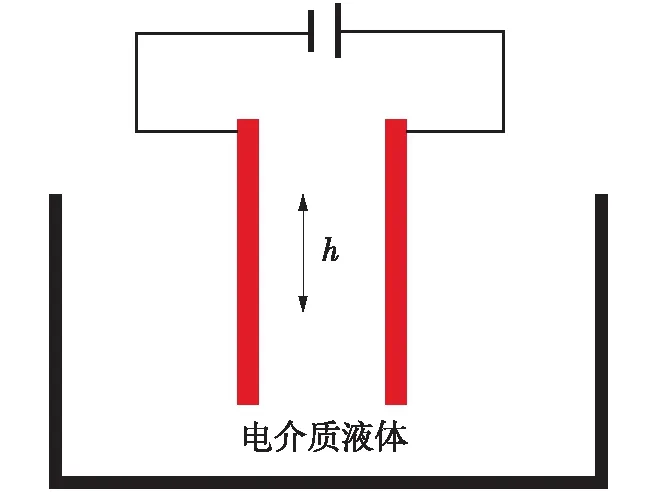
图3 液体在两个带电平行板间上升
2.3 静电场作用下混合气体组成的变化
式(12)表明,在静电场作用下混合气体的摩尔分数将发生变化。即图1的模型中,气体组分在电容器内、外的摩尔分数是不同的。由于相对介电常数ε大于1,摩尔分数在电容器内是增加还是减小由组分的摩尔质量决定。例如,对两组分混合气体,(M1-M)=(M1-M2)(1-y1),如果M1>M2,式(12)的右侧大于0,y′1>y1,即该组分在电容器内部的摩尔分数大于外部的摩尔分数。也就是说对于混合气体,摩尔质量大的组分在电场作用下其摩尔分数增加。由于介电常数和压强都与温度有关,因此温度也是一个影响摩尔分数变化的因素。现以甲醇-乙醇混合气体为例,设没有电场作用时两者的摩尔分数都为0.5。因为假设电容器内电介质占整个系统的比率很小,电容器外的摩尔分数固定不变。图4是由式(12)得出的甲醇-乙醇混合物中甲醇的摩尔分数随温度和电场强度的变化曲线。可以看出,由于甲醇的摩尔质量小于乙醇的摩尔质量,电容器内甲醇的摩尔分数变小了;温度越低,场强越大,摩尔分数的变化越明显。

图4 甲醇-乙醇混合气体中甲醇的摩尔分数随温度和电场场强变化(p= 20 kPa)
Fig.4 Variations of mole fraction of methanol in methanol-ethanol mixture gap with temperature and electric field (p=20 kPa)
式(12)表达出的物理含义为气体的富集或控制混合气体摩尔分数提供了一种新的思路。利用静电场可以增加某些气体成分摩尔分数的特征,可以收集有毒有害气体或一些稀有气体。而在某些特殊情况下,例如航天飞机上需要准确控制燃料的混合比例,也可以通过静电场作用来实现[24]。
2.4 静电场作用下液体混合物组成变化
式(15)表明,在静电场的作用下,混合液体中组分的摩尔分数将发生变化。即图1中电容器内液体的摩尔组成与电容器外不同。电容器内密度较大的组分的摩尔分数增加,密度较小的组分的摩尔分数减小。摩尔分数的变化率与电场强度的平方成正比。
除电场强度外,静电场的作用效果还与温度密切相关。因为式(15)的右侧除直接与温度成反比外,液体的密度和介电常数也随温度发生变化。液体的密度与温度的关系可以近似用饱和液体密度的经验公式ρ=AB-(1-T/TC)n表示[25]。以甲醇-乙醇混合液体为例,设没有电场作用时两种组分的摩尔分数都是0.5。图5是依据式(15)得出的甲醇-乙醇液体混合物中甲醇的摩尔分数随温度和电场强度的变化曲线。这个图形显示出一个奇特的现象,温度在301.4 K时出现交叉。在这个温度点上,电容器内部甲醇的摩尔分数是0.5,与电容器外部相同;而在该温度点的左侧甲醇的摩尔分数小于0.5,右侧大于0.5。出现这个转折点的原因如下:式(15)右侧的符号决定于混合液体中组分的密度。对于密度较大的组分,右侧为正,x′i>xi,静电场作用下该组分的摩尔分数增加;反之,对于密度较小的组分,其摩尔分数减小。当两组分的密度相等时,式(15)的右侧等于0,x′i=xi,组分的摩尔分数没有变化。也就是说静电场的作用效果依赖于组分的密度,密度差别越大,摩尔分数变化越明显;当混合物中各组分的密度相等时,电场没有作用效果,无论电场强度多大。对于甲醇-乙醇二元混合物,当温度低于301.4 K时,甲醇的密度小于乙醇的密度,甲醇的摩尔分数减小;当温度高于301.4 K时,甲醇的密度大于乙醇的密度,甲醇的摩尔分数增加。当温度等于301.4 K时,甲醇和乙醇的密度相等,电容器内甲醇的摩尔分数没有变化。
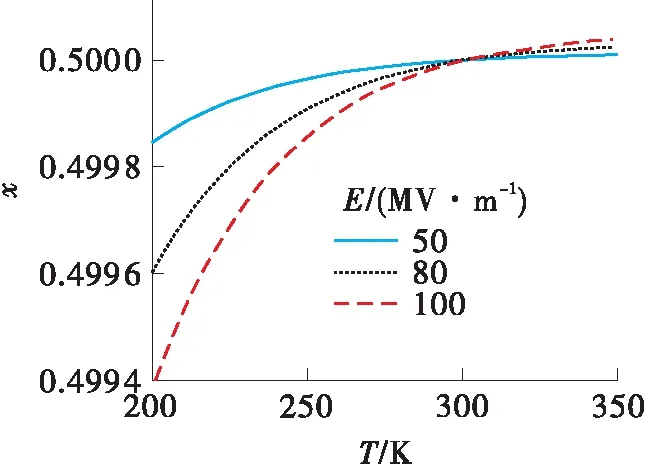
图5 甲醇-乙醇混合液体中甲醇的摩尔分数随温度和电场强度的变化曲线
Fig.5 Variations of the mole fraction of methanol in methanol-ethanol mixture liguid with temperature and electric field
比较式(6)和式(9)的数值计算以及比较图4和图5可知,在相同强度的电场作用下,液体的压强和摩尔分数的变化大于气体的压强和摩尔分数的变化。也就是说电场对液体的作用效果大于对气体的作用效果。这是因为液体的介电常数大于气体的介电常数,液体比气体更容易吸收电场能量。
液体混合物的组成比例(摩尔分数)对液体的折射率、表面张力、粘度和导热系数等物性参数都有较大的影响。利用静电场可以改变液体混合物摩尔分数这一特性可以对混合液体的物理性质进行有效地观测和调控。
3 结论
基于相平衡基本原理,利用电场作用下化学势的表达式,导出了静电场作用下流体电介质的压强和摩尔分数的变化规律。静电场作用下流体的压强和摩尔分数都将发生变化,变化的大小与电场强度的平方成正比,还与温度以及电介质的摩尔质量、密度和介电常数有关。
静电场作用下气体和液体的压强都有上升,电场强度越大、温度越低效果越明显。气体压强上升可能导致凝结,液体压强上升为测量介电常数提供了一种可能。静电场对液体的作用效果大于对气体的效果。在静电场作用下,混合气体的摩尔分数将发生改变,摩尔分数增加或减小决定于组分的摩尔质量,摩尔质量大于混合物平均摩尔质量的组分摩尔分数增加;这个特性可以用于气体的富集或混合气体组成的调控。静电场作用下混合液体的摩尔分数也将发生变化,摩尔分数的增加或减小依赖于组分的密度,密度大于混合物平均密度的组分摩尔分数增加;这个特性为电场调控混合液体的物理性质提供了一种可能。

