基于多变量LSTM模型对昆士兰州的电力负荷预测

朱振涛,陆思豪

(南京工程学院经济与管理学院，江苏 南京，211167)

2015年中共中央、国务院《关于进一步深化电力体制改革的若干意见》[1]的文件发布之后，全国各地的售电市场逐步放开。不同省份的电力市场交易模式虽然有不同之处，但交易方式还是以双边协商和集中竞价这两个交易方式为主，市场化程度逐步提升，从而吸引了众多售电公司涌入市场，希望在电力市场中获得更多收益。但是，随着电力市场改革的不断深入，售电公司的盈利不再容易，尤其是这次电力市场改革的前沿——广东省。

广东许多售电公司的盈利模式一开始可以按照原始价差模式进行盈利。但是2016年《广东电力市场交易基本规则(试行)》(以下简称《规则》)发布，《规则》对广东电力市场的成员、准入、注册、交易基本要求、交易周期和方式、计量与结算机制等作出了详细的规定[2]。交易结算机制对于电力大用户和售电企业进行偏差电量考核费用产生了较大的影响。偏差电量指的是用户实际用电量与月度市场电量(月度双边协商交易电量与集中竞争交易电量之和)的差额绝对值。偏差电量考核费用这种市场淘汰机制的出现让售电企业的风险大幅增加，获利空间被压缩，售电公司原本的盈利方式已经难以为继。

此外，即使在不久的将来广东的电力现货市场体系逐步建立与完善，偏差电量考核费用不再存在，其实质也是因为日前市场与实时市场联动机制的形成取代了偏差电量考核费用的位置，这些市场机制依然会对产生的偏差电量进行惩罚。并且由于市场的进一步完善，政府会进一步加强对可能危害电力市场的投机行为的监管，因此在《关于征求南方(以广东起步)电力现货市场系列规则意见的通知》中，市场下即使售电公司或者大用户通过投机方式从偏差电量中获得的收益也会被收回作为平衡资金。因此，在当前的电力市场发展背景下，售电企业使用更好的电力负荷预测方法实现更加精准的电力负荷预测对于其现阶段减少偏差电量，未来减少电费支出，从而降低成本，提升利润的意义愈加重要。

那么，在一个成熟的电力现货市场中，电力负荷的影响因素有哪些？如何使用预测模型来提高负荷预测的精度呢？由于中国的电力市场改革正在逐步推行中，尚未形成成熟规范的电力市场，因此本文将选择澳大利亚昆士兰州的电力交易和负荷数据来研究上述的问题。选择以昆士兰州为研究对象进行负荷预测，是因为澳大利亚国家电力市场是一个电力现货市场，且其区域定价策略对于中国建立电力现货市场依然具有一定的参考意义[3]。此外，澳大利亚国家电力市场建立于1998年，时间较长且较为成熟，相应的数字化建设较为完善，可以在互联网上查询到历史负荷数据以及相关影响因素的数据。这为负荷预测模型的算例提供了可靠的数据基础。

传统的短期和超短期电力负荷预测方法主要包括以往的经典负荷预测方法与传统机器学习预测方法这两大类，但是这两大类方法各有利弊，且无法同时解决时序性和非线性的问题[4]。而随着现在人工智能中深度学习方法的不断发展完善，长短期记忆网络(LSTM)在序列数据分析中表现优异，可以更好地克服上述问题。因此本文首先通过文献梳理电力负荷地可能的影响因素，然后建立基于多变量的LSTM的电力负荷预测模型；之后以澳大利亚昆士兰州为算例进行预测分析，并将预测结果与传统电力负荷预测方法的预测结果进行误差比较，并将不同影响因素组合的结果进行比较，以找出重要的影响因素。

一、电力负荷的影响因素分析

根据国外研究成果显示预测的实际电力负荷可以由趋势负荷、气象因素所引起的负荷变化、时间因素所引起的负荷变化和随机负荷变化叠加构成，其中随机负荷变化非常小可以忽略不计。此外还需要考虑到的就是电力市场下实时市场的电价波动导致的负荷变化[5]。因此，电力负荷影响因素可以概括为四种。

(一)历史负荷数据

历史负荷数据实际也就是趋势负荷，指的是随时间趋势变化的负荷，主要在一天24小时内上下班以及不同的季节或日期的变化中得到体现。本研究使用的是澳大利亚国家电力市场下昆士兰州从2014年11月10日到2019年12月28日每半小时间隔收集的历史负荷数据。这些数据来源于根据澳大利亚的《国家电力法》设立的AEMO(Australian Energy Market Operator,澳大利亚能源市场运行机构)的官方网站(http:∥www.aemo.com.au)。澳大利亚国家电力市场指的是澳大利亚东南部电网的电力市场，包括了五个州(昆士兰州、新南威尔士州、维多利亚州、塔斯尼亚州、南澳大利亚州)和一个首都直辖区(堪培拉)[3]，该电力市场的用电量占据全国的85%。

由于气候、时间因素数据收集上的限制，本研究将一天之内每半个小时的历史负荷数据转换为一天的平均负荷值。图1是这段时间内的历史负荷曲线图，从中可以看出位于南半球的澳大利亚夏季12月—2月期间负荷量显著较高，而秋季3月—5月、冬季6月—8月、春季9月—11月期间的负荷量明显低于夏季期间，用电负荷量具有随季节变化的规律性。

图1 2014年11月10日到2019年12月28日的负荷曲线图

陈卓等、陈亮等、姚朝等、王旭东等、张宇航等、李松岭在使用LSTM网络模型进行短期电力负荷预测时，只使用了历史负荷数据这一单变量[6-11]。此外，虽然辛永等、陆继翔、徐尧强等、徐先锋等、张明等使用多变量影响因素进行LSTM电力负荷预测，但是每篇文献中所有的多变量影响因素中都包含有历史负荷数据这一影响因素[12-16]。从文献[17]对历史负荷和当前负荷相关性分析得出的结论可以发现，去年同一时刻的负荷值对今年同一时刻的预测的负荷值相关程度低于这个时刻前的相邻连续时刻的负荷值，因此本文选取预测某时刻前的连续n个时刻的历史负荷值作为一个影响因素。

(二)气象因素

气象因素往往对于短期电力负荷预测有着非常重要的影响，其中常见的影响特征包括气温、相对湿度、风速、风向、降水量、气压、日照强度等。辛永等使用了一天之内的最低和最高温度作为气象因素，陆继翔等将气温、湿度、风速、风向、降水可能性、气压共六个特征全部纳入了气象因素进行考虑，张明等把气温、最低气温、最高气温、相对湿度、2分钟风速、10分钟风速、气压、最高气压一共多达八个因素纳入考量[12-13，16]。但是文献[15]通过交叉收敛算法(CCM)对用电量与天气因素的因果分析表明，相对湿度、风速、降水量都不是用电量的显著预测变量，只有气温是用电量的显著自变量。因此，本文选择最低与最高温度作为模型中描述气象类影响因素的指标。

昆士兰州面积大约为172万平方公里，州域广阔，州内具有三种不同的气候类型，大部分区域属于热带草原气候，但是昆士兰州主要人口却集中于该州东南角——属于亚热带季风性湿润气候的布里斯班市。该市也是人们经济活动的主要区域和最主要的用电区域，所以这里的温度变化可以作为昆士兰州温度变化的代表。本文从2345天气预报官方网站(tianqi.2345.com)选取从2014年11月至2019年12月的布里斯班市每日最低温度与最高温度作为影响因素。图2是其中2016年1年的最低和最高气温变化数据。观察图2可以发现，澳大利亚春、夏季即9月—2月最低和最高气温明显高于秋、冬季3月—8月的温度，其中6月、7月份澳大利亚温度相对较低，但也在零度以上。

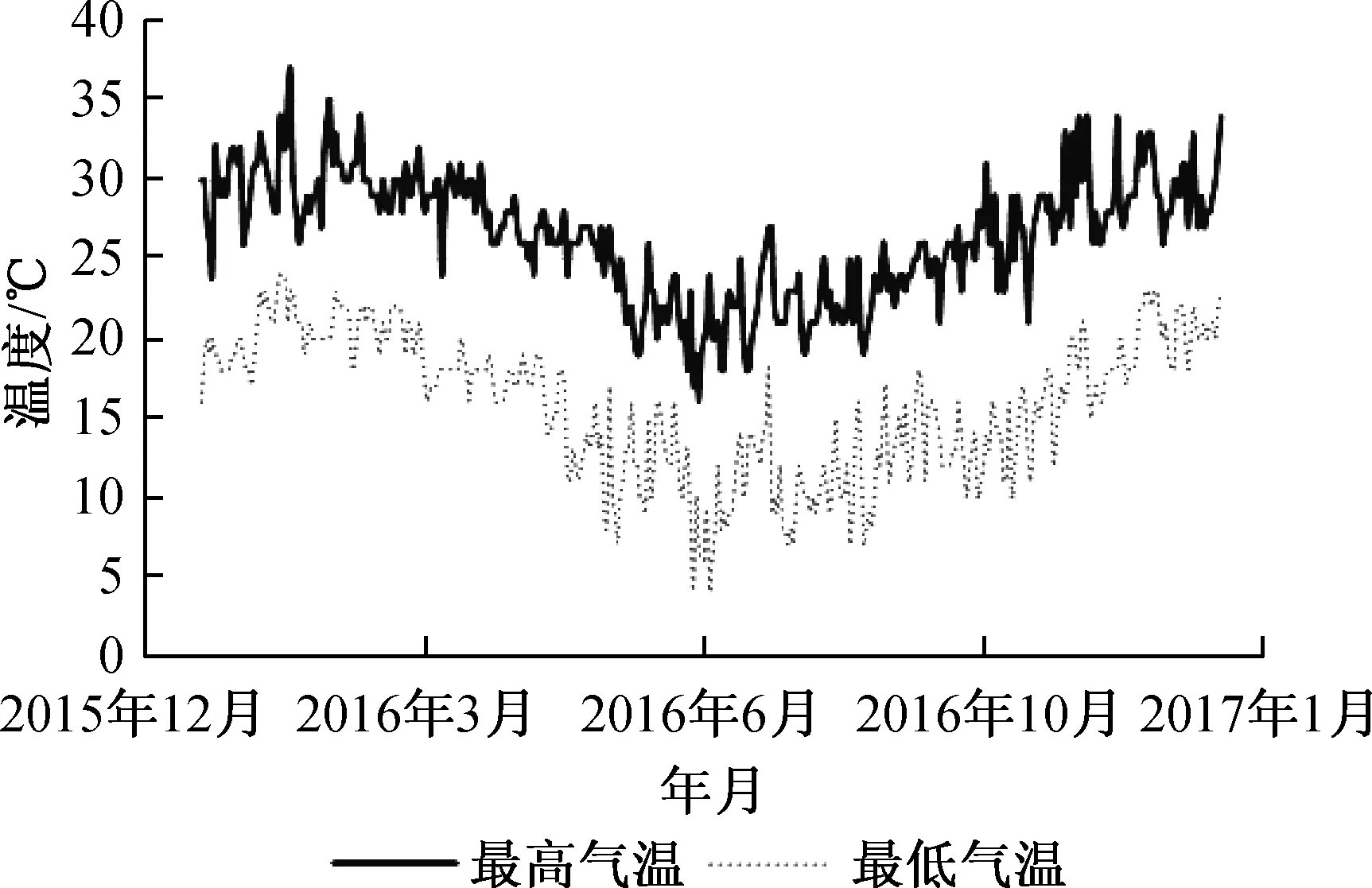
图2 昆士兰州布里斯班市2016年最低和最高气温曲线图

(三)时间因素

时间因素对于短期电力负荷预测也是一个非常重要的影响因素。李松岭、辛永等、陆继翔等、张明等都将日期或者时间类型纳入多变量影响因素的考虑范围，特别是工作日、非工作日、节假日这三种日期类型对电力负荷预测有着重要影响[11-13，16]。

澳大利亚昆士兰州的日期分为工作日、非工作日、节假日这三种类型。其中，非工作日是周末休息日，节假日则是澳大利亚昆士兰州的法定节假日。昆士兰州的法定节假日包括元旦(1月1日)、澳大利亚国庆日(1月26日)、耶稣受难日(每年北半球春分以后的第一个星期五)、复活节(延续耶稣受难日之后的星期六、星期日和星期一)、澳纽军团日(4月25日)、劳动节(每年5月的第一个星期一)、皇家昆士兰展览会(8月第三个星期的星期三)、英国女王寿辰(10月份的第一个周一)、圣诞日(12月25日)、节礼日(12月26日)这10个节日，上述法定节假日中元旦、国庆日、澳纽军团日、圣诞节、节礼日如果正好在星期六或者星期日，就向星期一延续。

而将不同的日期类型划分为工作日和非工作日是因为两者的时间段内用电方式是不一样的，所以用电量也会有所区别。此外，将节假日与工作日和非工作日划分开来，是因为节假日期间，人们并不像周末一样会待在家中休息，而是会参加一系列的户外庆祝活动。例如，在复活节期间昆士兰州就会有集体前往教堂进行礼拜、全国性民间艺术展、黄金海岸电影节、复古嘉年华、音乐节、歌舞剧巡回展等大型群众庆祝活动，人们会在外参加各种各样诸如上述的庆祝活动。本文将日期类型包括工作日、非工作日和节假日三种类型的分类变量作为影响负荷的可能影响因素。

(四)经济因素

近年来，随着电力市场改革，经济因素逐渐成为需要考虑的重要因素之一。陆继翔等、彭文等将电力价格纳入考量，前者考量的是随时间变化的电力市场出清价格，而后者则考量的是峰平谷固定电价[13,17]。

从图3可以看出，在经历了2008年全球金融危机以后，澳大利亚的GDP增长率除了2012年都在3%以下，经济整体相较于2008年前更为低迷，这主要是由于澳大利亚的支柱产业是包括金融、旅游等为主的服务业以及采矿业。虽然2008年的金融危机对服务业及采矿业形成了猛烈冲击，但是由于各种复杂的原因，2008年以来澳大利亚的电力价格到2019年年中时已经飙升117%。澳大利亚2019年8月的一组数据显示，历史负荷数据选取的昆士兰州居民用电价格竟然已经达到了35.69澳分/千瓦时，在澳大利亚只低于南澳大利亚州的价格，是美国同期居民电价的2倍多，比欧盟平均电价要高20%左右。因此在澳大利亚经济持续低迷的背景下，电价持续大幅增长，用电量的变化必然受到影响。

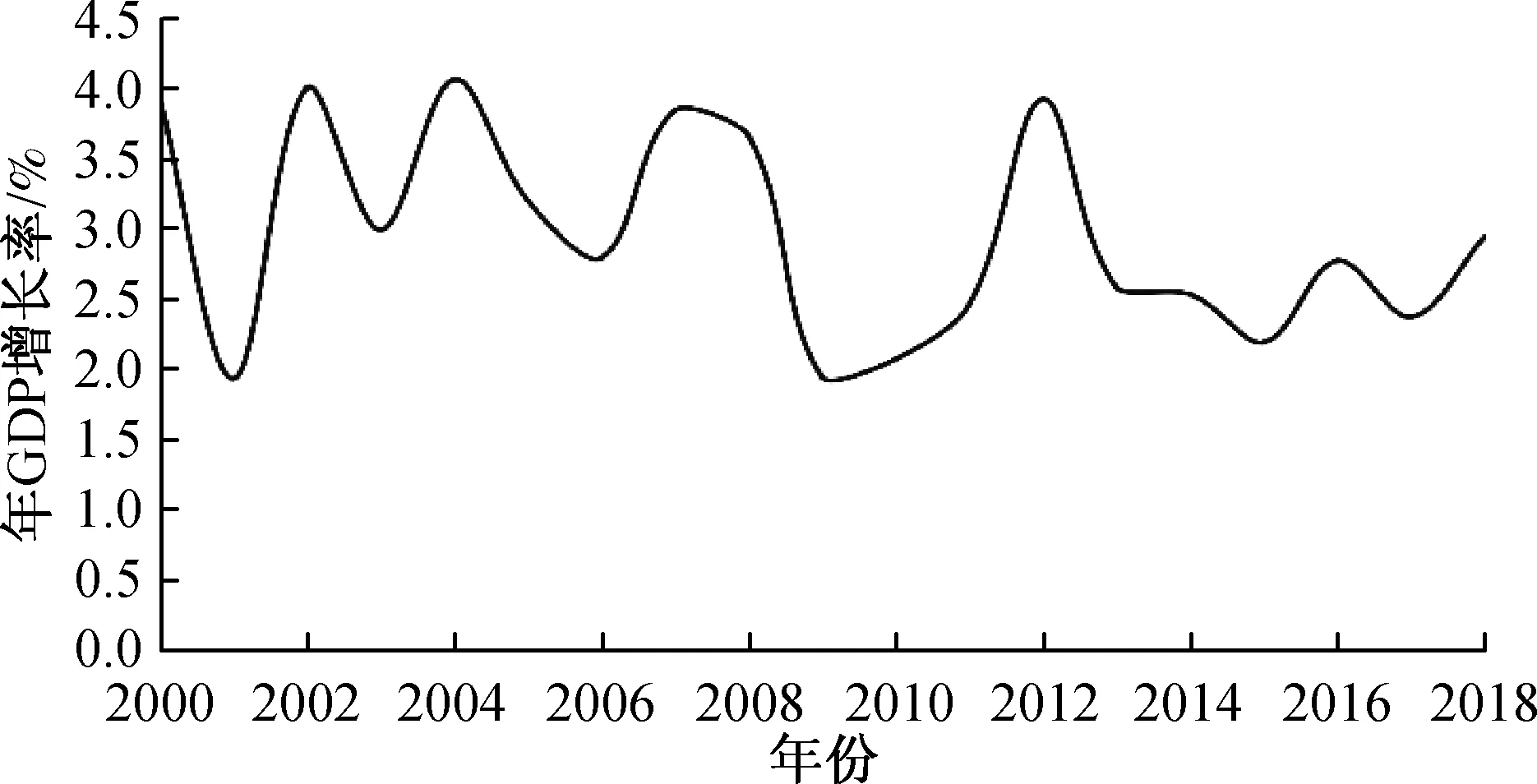
图3 澳大利亚2000年—2018年GDP年增长率

国内在考虑电价因素时受限于政府规定的峰平谷的固定电价，但是在一个澳大利亚这样较为成熟的电力现货市场中，电价是随着时间与负荷的变化而波动的。削峰填谷这一电力需求侧的管理行为不再由政府制定政策决定，而是由市场决定。本文使用的原电价数据是澳大利亚昆士兰州每天半小时的出清价格，这些价格数据与电力负荷采集时间点是一样的，同样来源于澳大利亚政府设立的AEMO官方网站。但是由于气象因素无法获得每半小时的数据，而只有一天的数据，因此本文将一天之内的48个电价数据求取成一天的电价平均值，作为影响因素。图4为某年12月份的电价和负荷曲线图。

图4 某年12月份电价和负荷曲线图

当负荷不断上升时供小于求，电价随之不断攀升，但是当负荷达到峰值时，电价也达到峰值，人们也会意识到电价过高而减少用电量，随之负荷下降，此时供大于求，电价随之降低。因此，本文将某时刻的电价也考虑作为可能的电力负荷的影响因素。

二、基于LSTM的电力负荷预测模型的构建

(一)电力负荷预测方法比选

传统的短期和超短期电力负荷预测方法主要包括经典负荷预测方法与传统机器学习预测方法这两大类。在经典负荷预测方法当中，多元回归模型、ARIMA模型(autoregressive integrated moving average model，整合滑动平均自回归)等方法着重考虑数据的时序性关系进行预测；灰色预测模型方法则致力于弱化数据的随机性，体现明显的规律性；专家系统预测方法是依赖于计算机中的像专家一样进行推理和预测的软件系统[18-21]。但是上述的方法在同时面对时序性和非线性的数据依然不能够进行更好的预测。而机器学习预测方法中的BP神经网络预测方法、随机森林预测方法等则对非线性关系的数据可以作出较好的预测，但是对于历史数据，这类方法并不能进行更好的处理[22-23]。

深度学习中的LSTM神经网络模型则可以同时更好地处理时序性和非线性关系数据。该模型相比于RNN，可以更加充分地回顾长期的历史负荷数据，而不容易出现梯度消失或者梯度爆炸的问题，并且作为机器学习的一个分支，其本身就能处理好非线性数据，因此，成为被选中的模型方法。

(二)LSTM模型

LSTM神经网络是在RNN基础上改进而形成的。LSTM由Hochreiter和Schmidhuber于1997年在LongShort-TermMemory中提出，截至2020年5月29日该研究文章的被引用次数已经到达了31 336次[24]，足以说明该模型在人工智能领域的巨大影响力。

由于LSTM模型源于RNN模型，下文先介绍一下RNN模型的结构和基本原理。RNN模型包括输出层、隐藏层、输入层。这三层，每一层都是由若干个神经元组成的，其结构如图5所示。

图5 RNN模型图

图5中的黑色方块表示一个延迟连接的装置，也就是连接上一个时刻的隐藏层状态S(t-1)到当前时刻的隐藏层状态S(t)之间的装置。而U、V、W代表三种不同类型的矩阵。U表示的是从输入层到隐藏层的权重矩阵、V表示的是从隐藏层到输出层的权重矩阵、W表示的是用隐藏层上一次的输出值来作为本次输入的权重矩阵[25]。图5展开后的循环如图6所示。

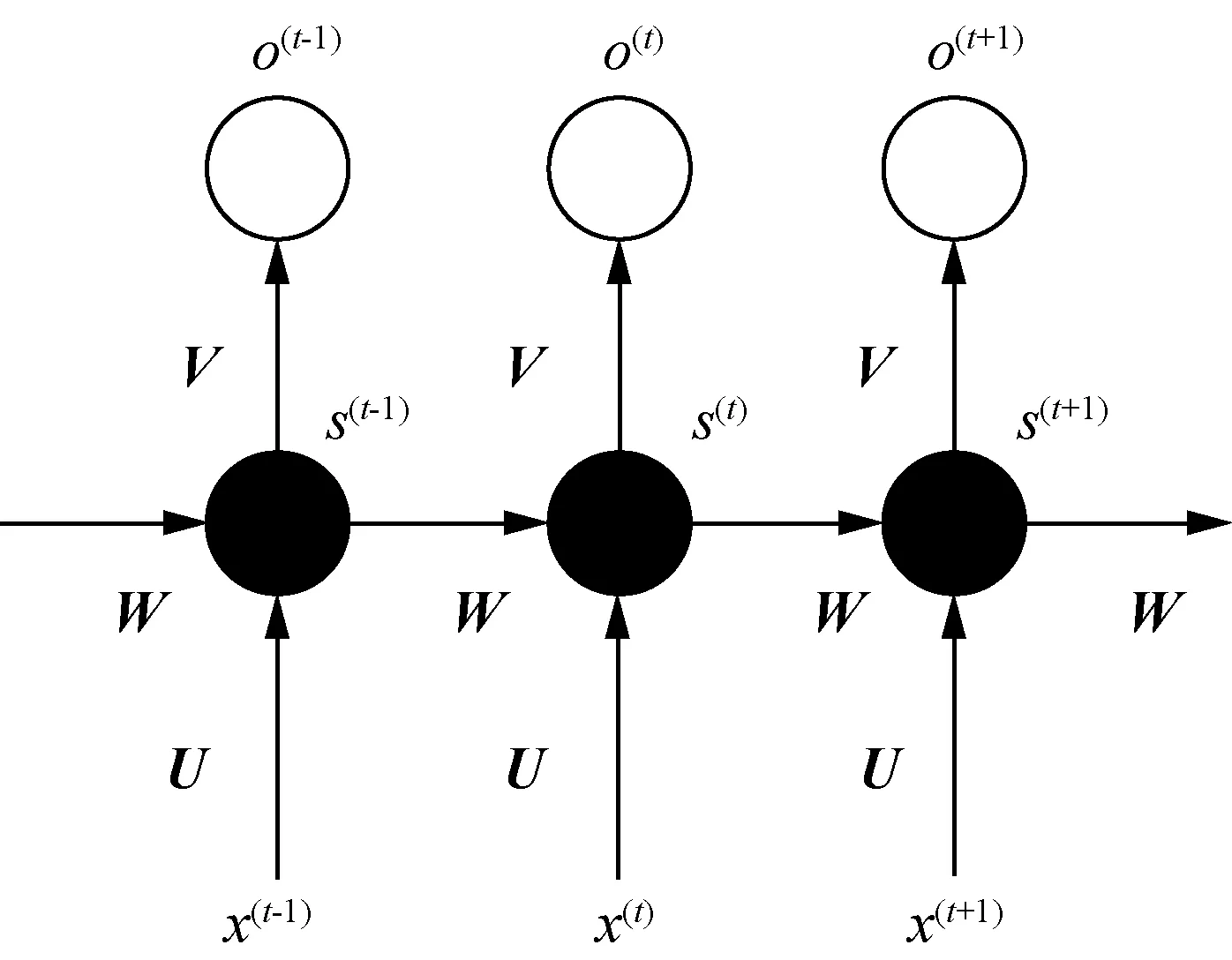
图6 展开后的RNN结构图

RNN展开后的循环模式用公式可以表示为：

s(t)=f(t)(x(t),x(t-1),x(t-2),…,x(2),x(1))

(1)

式中：s(t)为t时刻隐藏层的值；s(t-1)为t-1的时刻隐藏层的值；x(t)为t时刻的输入数据；σ为激活函数；θ为激活函数中所有参数的集合。

因此，在RNN模型当中，第t时刻的记忆信息，是由前(t-1)个时间步累积而成的结果s(t-1)和当前输入x(t)共同决定的。

RNN模型的运作方式与人的记忆一样，多次循环且不断更新，逐渐沉淀下来，慢慢形成先验知识。因此人的记忆的缺点，RNN模型也存在。当时序的间隔越来越大时，RNN虽然可以处理长期依赖的问题，但是，随着时间的继续推移，RNN模型越往后面的节点对更前面的时间节点的隐藏信息的感知力就越来越下降，也就是所谓的梯度消失问题；此外也有可能会有连乘的梯度趋于无穷大，造成整个系统的不稳定，这也就是所谓的梯度爆炸问题。正因为这两个问题，导致了RNN模型在越往后的预测中预测性能逐渐下降。所以，Hochreiter和Huber等对RNN进行了一系列的改进优化，并提出了LSTM网络模型，并逐步改良[24]。

LSTM网络在RNN的基础上增加了多个门(Gate),该模型的网络结构如图7所示。由图7可见LSTM网络模型结构是由遗忘门(Forget Gate)、输入门(Input Gate)、输出门(Output Gate)和记忆单元(Cell)组成的[26]。

记忆单元(Cell)是用于储存某一时刻的状态信息，而三个门是用来控制、保护和更新记忆单元状态。如图7所示，其中xt为当前时刻的输入,ht为当前时刻的输出。遗忘门部分由当前时刻输入xt和上一时刻输出ht-1经过Sigmoid函数共同输出ft,ft和前一时刻输出的状态记忆单元st-1共同来决定当前状态记忆单元中的需要遗忘的内容；在输入门部分中，当前时刻输入xt和上一时刻输出ht-1作为一个整体分别通过 Sigmoid函数和tanh函数之后产生这次新的信息it和可能需要的新信息ct，it和ct的乘积与遗忘门部分生成的当前状态记忆单元中的遗忘的内容一起生成当前时刻完整的状态记忆单元st，这也就意味着当前时刻的状态单元已经遗忘了需要遗忘的历史信息，而保存了新的信息，可以说遗忘门和输入门共同构成了当前的状态记忆单元，这相比于RNN就不会出现对过去历史信息的感知程度下降。而在输出门部分，由当前时刻的输入xt及上一时刻的输出ht-1通过Sigmoid 函数和已经通过tanh函数后的状态记忆单元st决定当前时刻的输出门状态ht，这说明输出层的状态实际和RNN模型的输出状态没有变，LSTM网络模型实际上变的就是对历史信息的一种处理方式，与人脑相类似，遗忘不重要的内容，记住重要的内容。各门、当前状态记忆单元st、当前输出ht的计算公式分别为式(2)-式(7)所示：

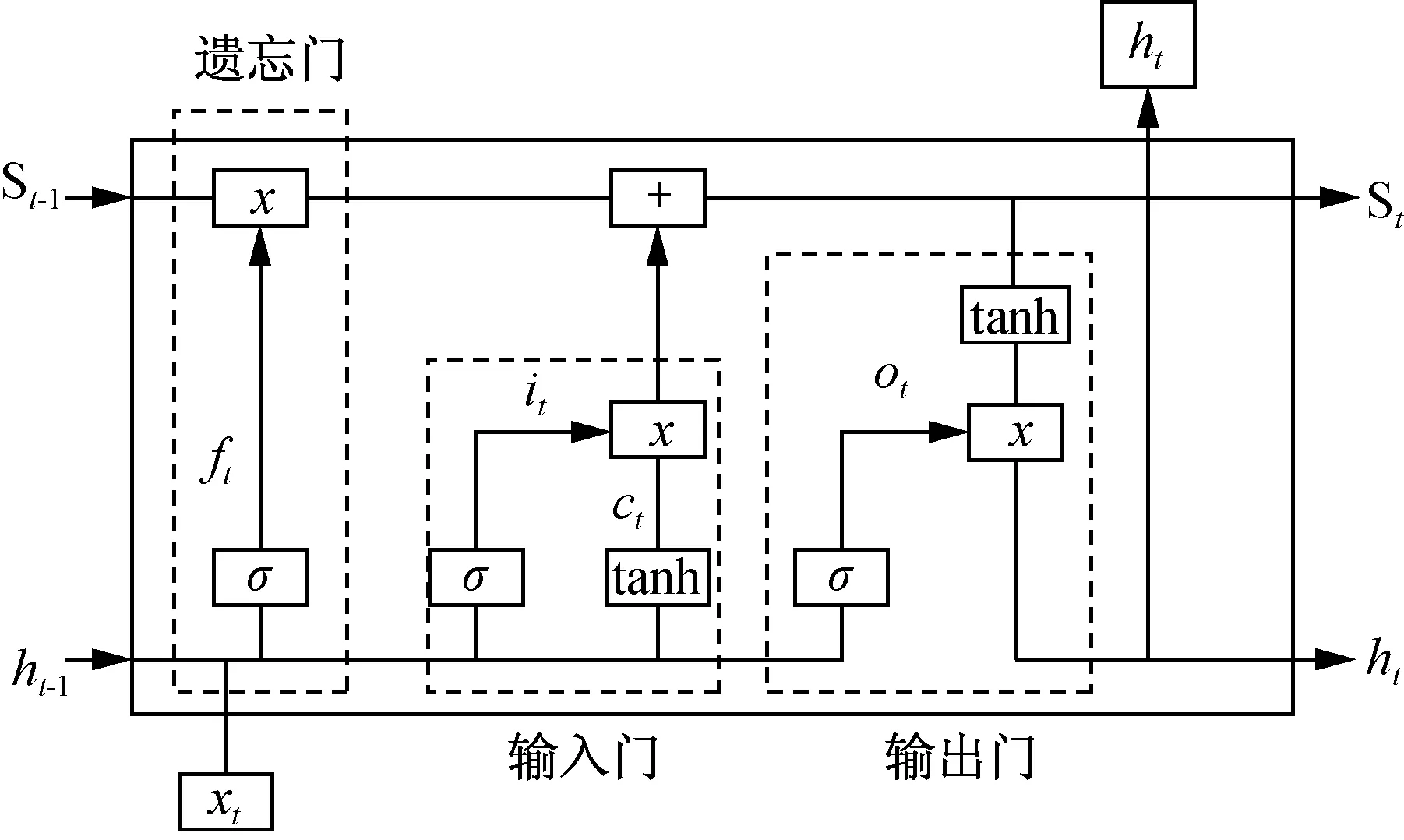
图7 LSTM网络基本单元图

ft=σ[wf(xt+ht-1)+bf]

(2)

it=σ[wt(xt+ht-1)+bi]

(3)

ct=σ[wt(xt+ht-1)+bc]

(4)

ot=σ[wt(xt+ht-1)+bo]

(5)

st=(it×ct)×(st-1×ft)

(6)

ht=tanh(st)×ot

(7)

式中：σ为sigmoid函数；w、b分别为对应门的权重和偏置项。

在进行电力负荷预测的LSTM模型当中，如果只是基于单变量进行电力负荷预测，那么在输入的单个变量就是一个单列的矩阵x。但是本文使用的是多个变量进行预测，因此就与单变量输入并不相同。输入的变量中包括历史负荷数据、电价、最低温度、最高温度和日期类型这5个因素。而前4个因素都是连续变量，所以需要输入列数为4的矩阵，并在输入之后进行归一化处理；而日期类型是一个分类变量，需要先使用独热(one-hot)编码将其化为虚拟变量，从而得到列数为3的矩阵。所以在5个因素纳入考量的多变量预测中需要输入列数为7的矩阵。而上述的输入变量就是xt,预测的结果是一天的电力负荷值就是输出变量ht。

LSTM模型需要调节的主要参数包括一个训练批次的大小、LSTM的层数、训练的次数、预测一天的电力负荷所需要考虑的历史天数。

(三)结果评价指标

结果评价指标使用误差指标当中的平均绝对百分比误差(MAPE)、均方根误差(RMSE)对算例分析结果进行最终评价。

MAPE的公式为：

(8)

RMSE的公式为：

(9)

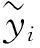
三、昆士兰州电力负荷预测算例分析

本算例先对所选的历史负荷数据和其他因素的数据中的错误或丢失的异常数据进行预处理，然后对所有的数据进行归一化的处理，去除这些原始数据的单位影响。这里使用min-max标准化方法将原始数据转换，使得数据大小可以统一在[0,1]这个区间上。

min-max标准化方法的公式：

(10)

式中：xnorm为标准化的数据；x为原始数据；xmax为原始数据中的最大值；xmin为原始数据的最小值。

(一)样本描述性统计

本算例使用的历史负荷数据是澳大利亚昆士兰州2014年11月10日至2019年12月28日的负荷数据。该日负荷数据的采样间隔时间为30分钟，每天一共会有48条数据，一共是89 990条历史负荷数据。由于在收集气象因素时只收集到一天的数据最低和最高气温，而无法获得采样间隔为30分钟的数据，因此，本文将每天48条的负荷数据转化为一天的平均负荷数据，这样就产生了1 875条日负荷数据。

澳大利亚的实时电力市场中价格数据采样也是每半个小时更新一次，每天48条。本文使用的是与负荷数据时间相对应的昆士兰州2014年11月10日至2019年12月28日的电价数据。电价也是基于气象因素数据收集的制约，本文将48条数据转化成一天的平均电价。

气象因素当中，本文选取的是从2014年11月10日至2019年12月28日每日的最低气温和最高气温，一共3 700条数据。

表1中描述的就是上面历史负荷数据、电价、最低温度和最高温度四个变量的平均值、中位数、最小值和最大值。

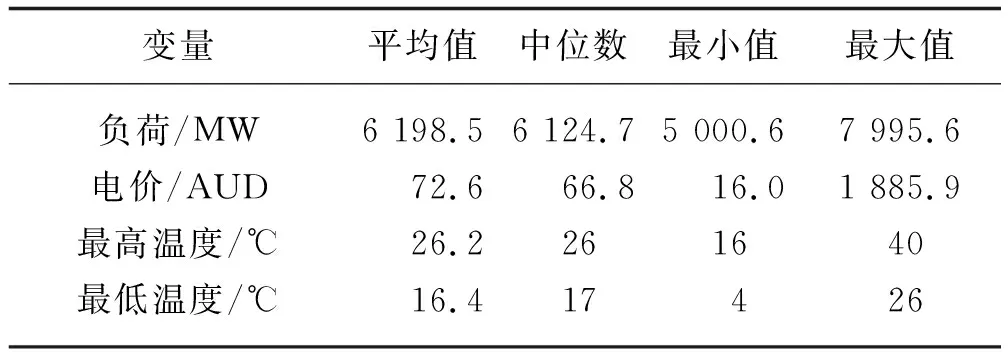
表1 数据集中主要连续型变量的描述统计

而在时间因素方面，考虑的就是工作日、非工作日、节假日这三种类型。从2014年11月10日至2019年12月28日，一共1 875天。从图8可以看出，其中工作日有1 288天(占比69%)，非工作日也就是周末一共有525天(占比28%)，节假日即澳大利亚昆士兰州法定节假日一共62天(占比3%)。

(二)结果分析

1.模型参数调优

在机器学习中，超参数是在开始学习之前设置的参数，在LSTM模型当中LSTM层数、一层的神经元个数、训练次数、一个批次的大小和训练所需要的前多少天都是超参数。这次算例分析中，将1 875 天当中的80%划分为训练集，20%为测试集。算例中用的是一层的LSTM网络模型，而一层的LSTM设置神经元个数为4，此外考虑到希望提高模型运算的运行速度，将一个批次的大小设定在60，并在固定的训练批次大小为60的情况下，不断改变训练次数，获得最佳的训练次数，同时这里设定使用前5天的影响因素预测第6天这一天的电力负荷。测试结果见表2。

表2 训练次数测试结果比较

经过上面的测试可以发现，当训练次数超过400之后，MAPE升高，RMSE在训练400次之后也逐渐上升，这意味着训练到500次时开始出现过度拟合，因此LSTM模型当中训练步数应该选择400次，此时LSTM为一层，一个训练批次的大小为60。

本文在上述已经确定的模型基础上再讨论应该使用预测结果这一天的前多少天数据进行预测，从1天开始带入模型，考察结果误差的大小，不同天数的MAPE结果如表3所示。

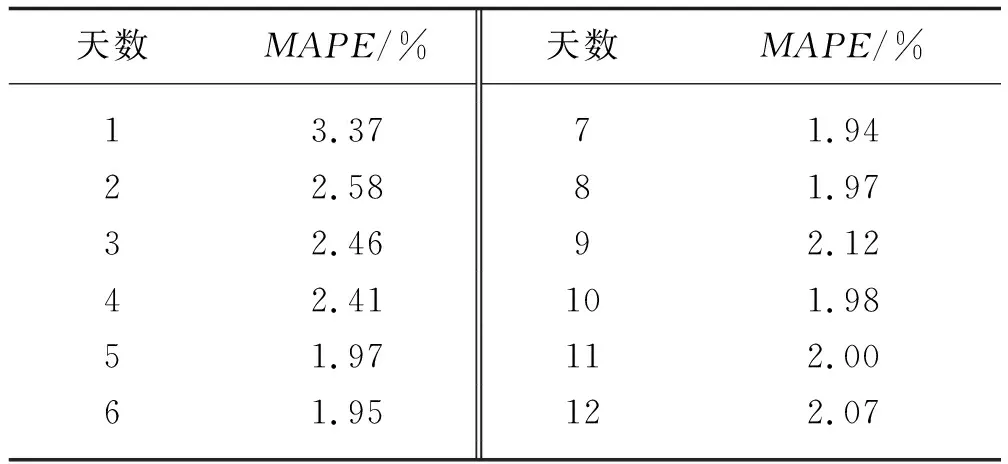
表3 不同历史天数情况下的结果误差比较

从表3可以看出，从前1天开始取，MAPE逐渐下降，一直到前7天时，MAPE到达最小值，之后又逐渐上升，这意味着从前8天开始，出现过度拟合的情况，因此我们取最优的前7天。

2.算法误差计算

用前7天的历史负荷数据、温度、电价和日期类型四种影响因素对第8天这一天进行电力负荷进行预测，可以观察到迭代次数下的训练误差和测试误差(图8)。前期随着训练步数的增加，误差大幅度降低，但是训练50次之后，误差变为逐渐减小，并最终趋于平缓。模型中所用的损失函数是平均绝对误差MAE，表示的是预测值和真实值之间的差值平均数。

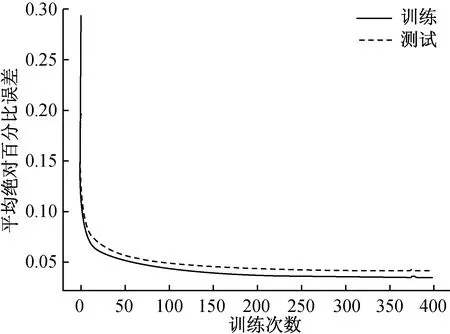
图8 训练和测试误差图

在上面的训练结束之后，本文得到最后的测试集中的结果，本算例中电力负荷的预测值和真实值对比如图9所示。

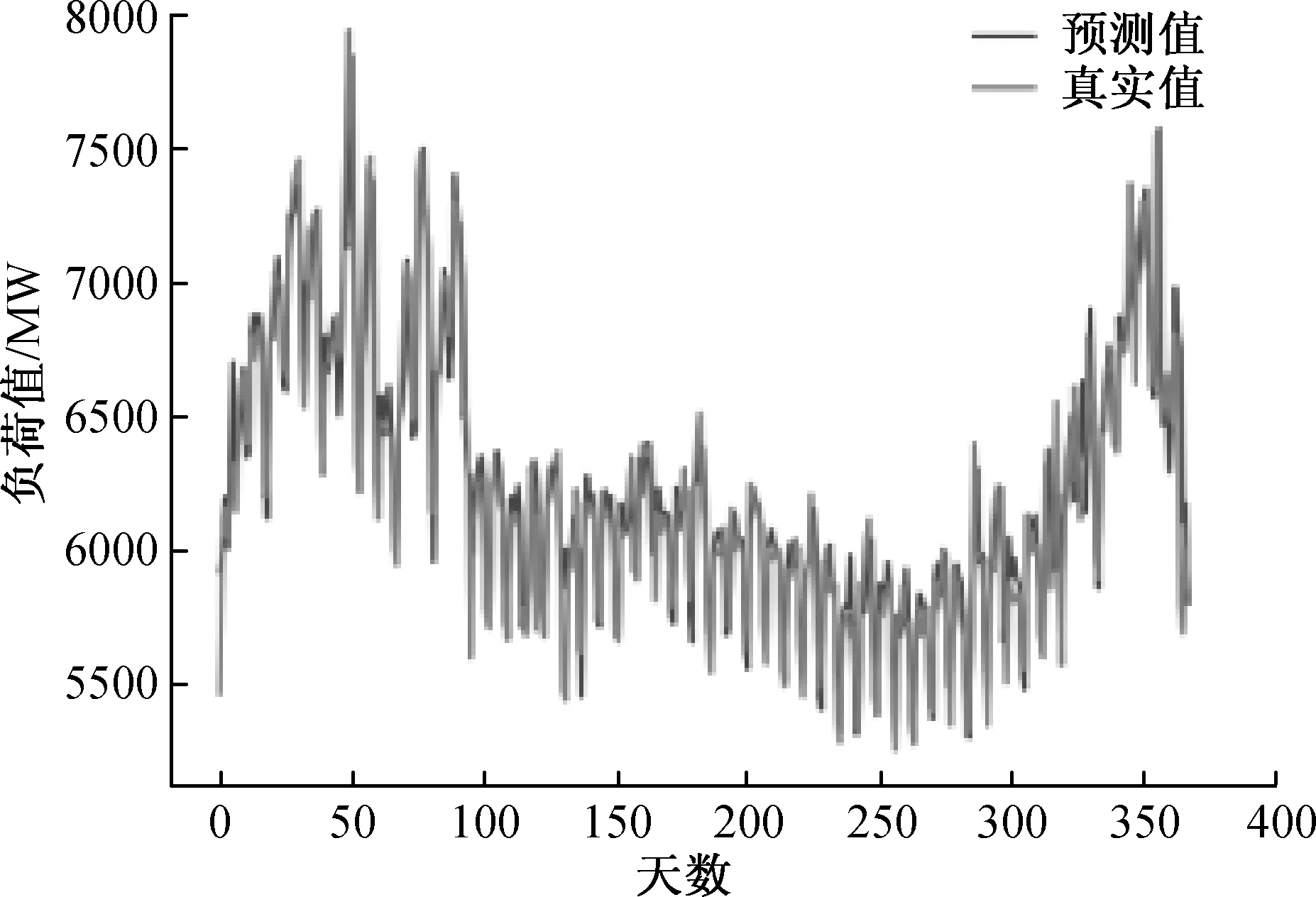
图9 LSTM模型的电力负荷预测值和真实值对比图

3.误差对比分析

如果使用经典的电力负荷预测方法中的ARIMA模型进行电力负荷预测误差结果为均绝对百分比误差(MAPE)为2.13%、均方根误差(RMSE)为192.20MW，与基于LSTM的电力负荷预测模型结果对比如表4所示。

表4 基于LSTM和ARIMA的电力负荷预测结果误差对比

所以基于LSTM模型的电力负荷预测误差比基于ARIMA模型的电力负荷预测的结果误差更小，预测结果更加准确。

4.不同因素影响下的误差结果对比分析

本算例使用LSTM模型对在其他不同影响因素组合下的电力负荷预测进行了测试。误差结果如表5所示，D为历史负荷数据,P为电价,THT为最高温度，TLT为最低温度，Type为日期类型。

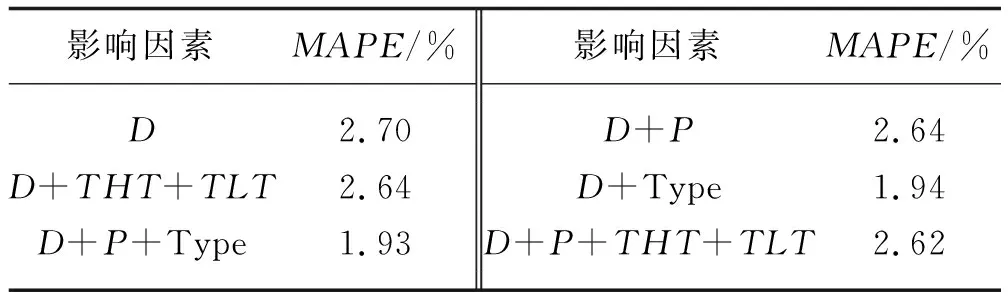
表5 不同影响因素下的电力负荷预测误差结果

从表5中可以看出，只使用历史负荷数据进行单变量预测时，效果并不是很好。在所有增加的单个因素中能最大程度减少预测误差的因素是日期类型，可以减少预测误差0.76%。另外，在历史负荷数据基础上加入电价这个变量，预测的误差结果相比较之前有0.06%的下降，但是不如在历史负荷数据基础上加入日期类型这一因素时的误差下降的明显(下降0.76%)。在历史负荷数据中加入最低与最高温度时误差也下降了0.06%，但是把加入历史负荷数据和最低与最高温度的时候，预测误差又下降0.02%，这说明电价的影响更强。

在所有添加两个因素的组合中，能带来预测误差最大下降量的是在负荷的历史数据之外还考虑日期类型和电价这两个因素，相比与只有单个负荷历史数据，可以使得预测误差下降0.77%。但是加入电价和最高与最低温度时误差下降就不如加入前面两个因素的误差结果明显，但是比加入之前又下降了0.02%，这说明实际上电价的影响对比于最低与最高温度更强。在有历史负荷数据、电价、最低与最高温度的基础上再加入日期类型，也就是所有要素都考虑在内，整个结果误差相比较之前下降到了1.94%，下降明显。

综上，除了负荷历史数据之外，日期类型、电价因素和最低与最高温度也是可以提高预测精度的影响因素。其中，日期类型的影响最强，其次是电价因素，最后是最低与最高温度。算例结果中电价可以促进预测误差的减小，但是影响不如日期类型明显。

四、研究结论

(一)研究总结

本文首先通过阅读文献归纳总结出四种影响电力负荷的影响因素：历史负荷数据、气象因素、时间因素、经济因素，然后在Kreas下建立基于LSTM的电力负荷预测模型，然后以澳大利亚昆士兰州为算例进行分析，结果与基于ARIMA的电力负荷预测结果进行比较，并将不同因素影响下的算例结果分析进行比较，得出结论：

(1)基于LSTM的电力负荷预测模型的预测误差比传统ARIMA模型的预测误差更小，适合于短期负荷预测。

(2)除了负荷历史数据之外，日期类型、电价因素和最低与最高温度也是可以提高预测精度的影响因素。其中，日期类型的影响最强，其次是电价因素，最后是最低与最高温度。

(二)研究展望

本文使用的研究方法取得了较好的预测结果，但是仍有空间提升电力负荷的预测精度，未来研究还可以改进的几个方面有：

(1)2020年1月，因为受到突发新冠肺炎疫情的影响，广东电力市场下发通知，豁免所有售电企业、大用户、发电企业的1月、2月份的偏差电量考核费用。中国全社会用电总量在2月大幅度下降，直到目前复产复工率不断攀升，才恢复到接近历史负荷值。在进行电力负荷预测的时候我们需要将此类的黑天鹅事件纳入影响因素的范围，从而提高模型的预测精度。

(2)由于数据收集的限制，无法将每半小时的历史负荷数据、电价作为影响因素加入模型，本文无法预测一天之内的负荷变动情况，因此可以在未来的研究当中将更加精确的温度、历史负荷数据和波动的市场出清电价纳入考量，从而提高负荷预测的精度。

(3)以广东为起步的南方电力市场还是中长期市场规则中有偏差电量考核机制，对电力负荷预测具有较高的要求，但电力价格无法像现货市场一样实时波动且公开负荷数据较少，所以本文采用的是澳大利亚电力市场中的电力负荷与电价数据。未来几年内，包括广东、浙江省在内的地区正在逐步建设全面的电力现货市场，但从表6可以发现澳大利亚是单一的电力现货市场，这些地区很难去模仿这样的单一电力现货市场，因为这样的市场环境下，电力供应可能会出现紧张，导致电力价格波动较大[3]。

表6 澳大利亚国家电力市场与美国PJM电力市场对比

目前各个省份的电力市场改革情况反映有可能出现相似于美国PJM市场一样的电力市场，从表7可以看出，PJM电力市场相比于澳大利亚国家电力市场多出容量和日前市场等市场，在这样的情况下电价主要包括电能电价、容量费、输电费等，经济因素中电价的构成与澳大利亚现货市场中电价的构成并不相同，且PJM电力市场因为有日前市场所以结算方式也不相同，在影响电力负荷预测结果上可能会有区别，但是实时市场每五分钟产生的市场出清价格与澳大利亚电力市场中的出清价格没有太大区别。此外，澳大利亚电力市场中将区域中的某一个节点作为整个区域的参考电价，而PJM市场中边际节点价格需要根据不同的地点变化，因此在考虑电价的同时还需要考虑气象因素更准确地测量地点，但是历史负荷数据及气象因素如温度、风向等整体也没有太多区别。因此，基于LSTM模型进行的电力负荷预测这一技术在与相似于PJM的中国未来电力市场下依然是可以实现的。