花样滑冰跳跃动作中的力学原理1)
刘广彦 程修妍 刘海燕 白若阳 李海龙 吴 霞 王 宁
*(北京理工大学宇航学院,北京 100081)
†(中央广播电视总台,北京 100020)
第24 届冬季奥运会,全世界体育迷的目光再次聚焦在了北京的奥运赛场上。花样滑冰是冬奥比赛中一个极具观赏性的冰上运动项目,它结合了技巧性和艺术性,项目中的运动员通过冰刀在冰面上划出曲线,并表演跳跃和旋转等高难度动作,用《洛神赋》中的话可以描述为“翩若惊鸿,婉若游龙”。我们可以看到冬奥比赛中王诗玥/柳鑫宇在冰面上时而快时而慢地旋转,动作非常潇洒优美;同样可以看到羽生结弦起跳后身体突然快速旋转去挑战阿克赛尔四周跳(Quad Axel,4A) 这一从未有人在公开赛场上实现过的极限跳跃,非常令人惊叹!那花样滑冰运动员是如何做到这些高难度动作的呢?本文将围绕花样滑冰中的关键动作解读其中蕴含的重要力学原理。
1 花样滑冰跳跃动作中的力学原理
跳跃动作是花样滑冰所有技术动作中难度最大的,也是花样滑冰的灵魂和取胜的关键,所以教练员和运动员都极为重视。根据跳跃动作的特点,可以划分为助滑、起跳、空中和落冰四个阶段[1]。
1.1 助滑阶段
花样滑冰跳跃动作的第一个阶段是助滑,助滑的主要目的是让运动员获得一定的初速度,这一阶段运动员主要做平动,也就是说整个身体大致朝一个方向运动,身体转动的幅度很小。
1.2 起跳阶段
花样滑冰跳跃动作的第二个阶段是起跳,起跳阶段有两个主要任务,一个是使运动员获得垂直冰面向上的速度,这个速度的大小决定了运动员的跳跃高度,在一定程度上也决定了腾空的时间,运动员要在这段时间内完成预定的空中旋转动作。在这一瞬间的起跳动作就遵循着一个重要的力学定理——动量定理。为了产生竖直向上的速度,运动员起跳时要用力蹬冰,冰面就会对人体产生作用力,这个作用力通常有一个水平方向的分量和一个竖直向上的分量(图1)。由动量定理可知,在竖直方向上运动员受到的力的冲量等于运动员在该方向上动量的改变量

图1 运动员起跳时受力分析

式中,下标z表示垂直冰面向上的方向,等号左边为运动员在竖直方向上动量的改变量,其中第一项mvz2为起跳结束瞬间的动量,第二项mvz1为起跳前一瞬间的动量。等号右边的Iz表示起跳过程中运动员受到的竖直方向的力所产生的冲量。当冰面作用力在竖直方向的分量大于运动员的重力时,这个冲量的方向竖直向上,运动员就获得了一个向上的起跳速度。
起跳阶段的第二个任务是让运动员的身体转动起来,为后续在空中以更高的速度旋转做准备。一方面,运动员通过助滑获得了一定的速度,但这时候运动员主要做平动,起跳前运动员的双腿可分为支撑腿和摆动腿,运动员可以通过支撑腿的突然制动,也就是身体偏心的制动使其运动形式发生改变,由平动转变为转动,这是运动员在起跳时实现转动的一个因素。另一方面,运动员支撑腿的冰刀与冰面相互作用,冰面对冰刀的作用力对运动员起跳旋转时的转轴产生力矩,这个力矩是让运动员旋转起来的另一个因素。比如我们站在地面上可以突然起跳并转身,这就是因为地面对身体的作用力产生了一个力矩,这个力矩让我们实现了身体的转动。这里涉及到另一个重要的力学定理—— 动量矩定理,物理上叫做角动量定理。对于做定轴转动的物体来说,它对转轴的动量矩可以用Lz表示,即

其中Jz为物体对转轴z的转动惯量,ω为物体旋转的角速度。根据动量矩定理

物体对转轴z的动量矩随时间的变化率等于作用在物体上的外力对该轴的矩Mz,可见外力矩可以改变运动员的动量矩,所以冰面对人体的作用力所产生的力矩可以让运动员旋转起来。
另外,在花样滑冰双人滑中有一个惊险刺激的动作—— 抛跳,抛跳时男运动员双手扶着女运动员的腰部或者一手拉手一手扶腰将女运动员抛出去,这时男运动员对女运动员施加了一个力偶,也就是一对大小相等、方向相反、作用线平行的两个力。抛跳时给女运动员施加力偶就是对她的旋转轴产生了矩,这是双人滑抛跳时女运动员动量矩的主要来源。
1.3 空中和落冰阶段
起跳后运动员进入第三个阶段—— 空中旋转阶段,这时运动员只受重力的作用,当重力通过转轴时,外力矩等于零,所以运动员无法像起跳阶段那样通过外力矩来改变动量矩从而改变角速度。但我们看到运动员起跳后角速度会迅速增大,在腾空的短时间内可以旋转三周或四周,然后落冰时再把角速度降下来实现平稳着地。在没有外力矩的情况下运动员是如何改变角速度的呢?根据动量矩定理(式(3)),当公式的右边即外力矩为零时,动量矩随时间的变化率等于零,也就是说动量矩为常数,这就是动量矩守恒定律。如果Lz为常数,那么Jzω亦为常数。此时如果想增大或减小角速度ω,其实是可以通过改变转动惯量Jz来实现的,减小转动惯量角速度就增大,增大转动惯量角速度就减小。转动惯量是描述物体转动惯性大小的物理量,转动惯量越大的物体越难转动,也就是不容易使其角速度发生改变。如图2 所示,对于物体中的任何一个质点i,假设它的质量为mi,到z轴的距离为di,那么这个质点对这根轴的转动惯量就等于mid2i。图中物体可以看作是由若干质点组成的质点系,对所有质点对z轴的转动惯量求和就得到了整个物体对该轴的转动惯量,可见转动惯量不仅和物体的质量大小有关,还和质量分布以及轴的位置有关,质量分布离轴越远转动惯量也就越大。
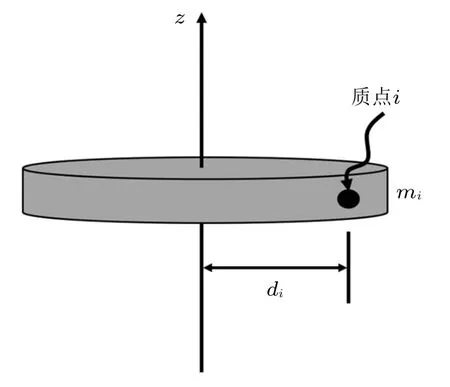
图2 物体中质点对轴的转动惯量
例如,图3 所示霍伯曼球是一个常见的可以自由伸缩的玩具,当用一根细丝从球中间穿过时,拉动和松开细丝可以实现球的收缩和伸展。如果给球一个初始的角速度使其旋转起来,然后拉动细丝使其收缩,可以看到球的角速度会明显增大。再松开细丝使球伸展,又可以看到球的角速度会明显变慢。这个过程中霍伯曼球的质量没有发生变化,但质量分布发生了改变,所以球对转轴的转动惯量发生了改变。由于动量矩守恒,转动惯量的改变就引起了角速度的变化。

图3 霍伯曼球
根据以上动量矩守恒定律和转动惯量的概念,可以解读花样滑冰运动员空中旋转的奥秘。当运动员腾空绕身体纵轴旋转时满足动量矩守恒定律,要想拿到更高的旋转分数,可以靠减小转动惯量来增大旋转角速度,进而在一定的腾空时间内完成更多的旋转周数。运动员起跳后双腿迅速伸直朝身体纵轴靠拢,同时双臂也收紧尽可能靠近身体纵轴,这样就使得身体绕转轴的转动惯量非常小,身体进入快速旋转状态。落冰前运动员的手臂和腿均有一定程度的打开,这就使得身体绕转轴的转动惯量增大,身体旋转的角速度减小,从而实现稳定落冰。
其实通过调整身体姿态来改变转动惯量,从而改变旋转速度的原理,不仅应用在花样滑冰等竞技体育上,在我们的生活中也常见到。比如我们过独木桥时会把双臂打开就是为了增大身体对转轴的转动惯量。另外,猫旋也是一个非常典型的例子。人们常说猫有九命,即使四脚朝天从高处落下,猫也能在空中迅速旋转身体最后四脚着地而不受损伤。文献[2-3] 对此进行了研究,发现猫在开始下落时先从中间弯曲身体,然后前腿收缩靠近上体躯干,上半身绕旋转轴的转动惯量很小所以可以迅速旋转180◦,同时它的下半身(包括下体躯干、后腿和尾巴) 尽量外伸以增大转动惯量,为了使总的动量矩守恒,下半身要朝相反的方向旋转,但转过的角度很小(5◦左右)。为了实现四脚着地,随后猫使后腿与下体躯干形成一条直线,并使身体绕这根轴反向旋转,这时下半身绕旋转轴的转动惯量很小,所以下半身也可以迅速转到腹部朝下的位置。同时,猫伸出前腿增大转动惯量以减小上半身的旋转速度,这个过程中还需要转动尾巴做一些微调使总的动量矩守恒。科学家用高速摄影发现猫旋整个过程仅需1/8 秒的时间,可以看出猫把动量矩守恒定律演绎到了极致。
动量矩守恒定律最早可以追溯到17 世纪初开普勒提出的行星运动第二定律,定律指出太阳系中的太阳和行星的连线在相等的时间内扫过的面积相等。这一定律实际上揭示了行星绕太阳公转的动量矩守恒。之后,动量矩守恒定律在天体探测、量子力学、卫星发射、航空航天航海等领域都有着非常重要的应用。
2 结束语
通过本文对花样滑冰跳跃动作的分析和解读,希望读者能够更加关注冬奥会上的花样滑冰比赛项目,并思考花样滑冰动作中涉及到的动量定理、动量矩定理和动量矩守恒定律等力学原理,也祝愿我国的花样滑冰运动健儿在冬奥会及其他重大赛事上取得好成绩。
致谢感谢中央电视台科教频道《实验现场》栏目的大力支持。

