旋转导向近钻头随钻伽马数据成像处理技术

孙轶伦，潘 磊，李海滨，王来智，周建新

（1.南京工业大学机械动力工程学院，江苏南京 211816；2.盘锦市辽河油田天意石油装备有限公司，辽宁盘锦 124010；3.宝鸡石油机械有限责任公司，陕西宝鸡 721002）

随钻伽马成像技术是近钻头地质导向系统的关键技术之一。钻井过程中，伽马密度仪上的探头实时扫描测量地层的放射性强度，提供相应深度处4个扇区或者6个扇区伽马值[1]。但现有随钻测井数据系统传输能力有限，无法将大量的扇区伽马成像数据实时上传至地面测控系统，不能及时了解测井处地质情况。为了实时获取近钻头处伽马成像图，使用插值方法分别将深度方向和井周方向获得的数据进行插值处理计算出连续的伽马值，对插值后获得的连续伽马值按照特定的色谱进行颜色映射处理，把颜色数据根据坐标位置绘制伽马值强度图来及时反映地层岩性，为钻井调整提供依据。

1 随钻伽马测量系统原理简介

目前，国内外常用的随钻地质导向作业测量技术就是近钻头伽马成像测井技术，在钻井过程中利用安装在钻铤侧面的多个伽马探测器定向探测特定扇区的伽马值强度，对各扇区获得的数据进行处理后，根据成像信息分析地层地质的变化，据此调整钻头前进方向，以实现地质导向作业[2]。

随钻测井（MWD）是实现精确钻井不可或缺的一环，其中如何实现较大信息量的随钻数据传输技术限制了MWD的发展和应用[3]。目前广泛使用的传输系统是较为可靠且经济性较好的泥浆脉冲数据传输系统，利用钻井液作为传输介质，在泥浆的流动通道内安装一个脉冲发生器，通过调节脉冲发生器的运动规律，使泥浆产生脉冲信号，井上的压力传感器接收到脉冲信号后对其进行解析获得数字信号，从而实现井下数据上传[4]。

自然界岩石中所含的铀、钍及其衰变产物和钾的放射性同位素能引起地层自然放射性。放射性元素在没有任何外界激发的情况下，可以释放出射线，这些具有放射性的元素在衰变过程中能发射α粒子、β粒子和γ射线。α粒子和β粒子穿透能力差，不能用于测井；而γ射线具有强穿透能力的高能电磁波，在钻井过程中能被探测到[5]。随钻伽马测量系统在钻井过程中测量不同性质地层的伽马射线强度，再将各个地层中的伽马测量值标定为单位API自然伽马标准值[6]。地层中的伽马射线进入伽马探测器后，由探测器将伽马光子转换成点脉冲信号，经过处理电路将信号变成标准脉冲，送入伽马井下探管的CPU处理电路。CPU利用内部计数器对其计数，并且每16秒采样一次伽马脉冲计数值，再取其单位时间内平均值，得到伽马脉冲计数率，通过刻度方法将伽马射线强度转换为自然伽马标准计量单位API存入非易失性存储器中。同时，标准伽马脉冲测量值通过总线的形式转送到MWD井下仪器，MWD探管SEA将伽马测量值与其他井眼几何参数，传输到MWD地面系统的计算机中，处理后得到与井深数据相对应的实时伽马曲线[7]。

2 插值方法

2.1 选择插值方法

插值过程需要满足以下条件：①插值点必须要经过已知的数据点和特征点，即已知数据和特征数据一定要满足插值公式；②重采样后的曲线要保持原有特征曲线的形状；③重采样后的曲线要保持和原有特征曲线的轮廓凹凸一致；④重采样后的曲线在离散的采样点之间插值要平稳，即要保持曲线的光滑性，需要保证所有的插值点具有连续的一阶导数或二阶导数[8]。

对井周数据进行插值处理时，可以得到在某个深度上测井所测得在同一平面360°方位均匀分布的4个或6个数据点，因此，采用三次样条曲线进行插值可以得到360°方位连续变化的二维曲线。

但是，对井深数据进行插值时，由于深度方向上的数据随着钻井过程不断更新，三次样条曲线的方法不能准确地进行曲线拟合，而Akima插值是一种局部插值方法[9–10]，不需要获取全部数据再进行插值，适用于对实时更新的数据进行插值，因此采用Akima插值方法进行拟合。

2.2 Akima插值方法

Akima插值方法是在两个测量点之间进行内插，建立一个三次多项式的方程，在进行内插的过程中，除了需要原本的两个测量点之外，还需要用到这两个点邻近的四个点的数值，即每得到一段光滑曲线，需要六个点的数值，并且要求曲线具有连续的一阶导数来保证曲线的光滑性。

设已知每个数据点的导数，对于任意两个相邻数据点xk和xk+1(k=0，1，2， ···，n )之间可以得到以下四个条件：

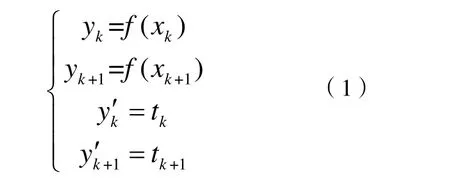
在 [xk，xk+1]区间对应的区间函数S(x)为一个三次多项式

通过式（2）可计算子区间中的插值点。

根据Akima几何条件，利用六个相邻数据点可以计算区间的插值公式，tk和tk+1可以用下式计算：

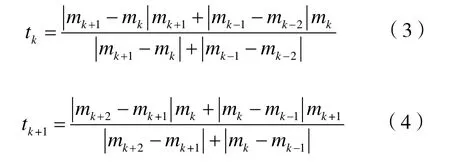
其中：

在开始和结束的端点处无法使用式（3）需要在端点外根据曲线的趋势补足两个点。现假设端点(xn，yn)和已知数据点 (xn-1，yn-1)、(xn-2，yn-2)，需要补上的数据点为 (xn+1，yn+1)、(xn+2，yn+2)，这五个点都在曲线S(x)上，并且：

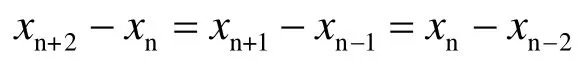
根据上式可得：

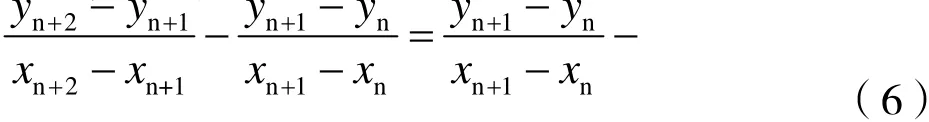
即：

可得到：

当mk=mk+1与mk-1=mk-2时，

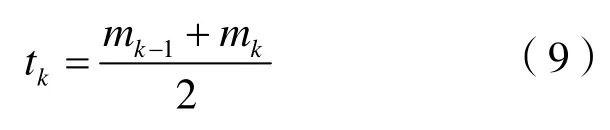
当mk+2=mk+1与mk=mk-1时，

最后，计算三次多项式S(x)的各项系数：

将式（1）和式（10）结合，可实现插值重采样。

2.3 三次样条插值[11–12]

设f(x) ∈c[a，b] 对 区 间 进 行 划 分：a=x0＜x1＜···＜xn=b，区间内每个节点的函数值yk=f(xk)(k=0，1，2， ···，n )在区间[a,b]上的样条函数S(x)需要满足下列三个条件：①对任意区间[xk，xk+1]，S(x)是三次多项式；②整体上二阶连续，即S(x) ∈c2[a，b]；③满 足插 值条件S(xk)=yk(k=0，1，2， ···，n)。

构造一个三次样条插值函数一般有两种方法：①以节点处的导数值为参数构造三次样条插值函数，利用插值节点上的一阶导数作为未知量，然后利用二阶导数在内点连续条件来求出方程的解；②以节点处的二阶导数值为参数构建三次样条插值函数，利用插值节点上的二阶导数作为未知量，然后利用一阶导数在内点连续条件来求出方程的解，文中采用第二种方法。

其中，hi=xi+1-xi，根据条件S(xk)=yk，S(xk+1)=yk+1确定积分常数，得到三次样条表达式（13）。式（12）和（13）中的Mi(i=0，1，2， ···，n)未知，对S(x)求导得到Mi的值。

S(x)的一阶导数连续，因此：

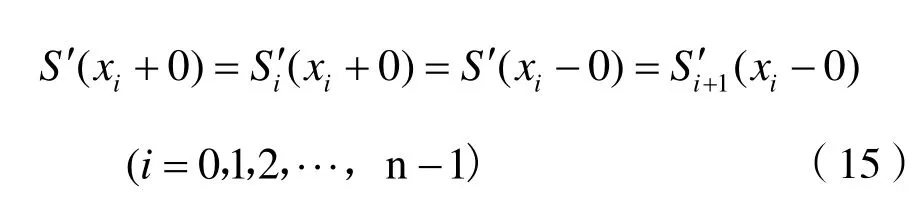
可得到：

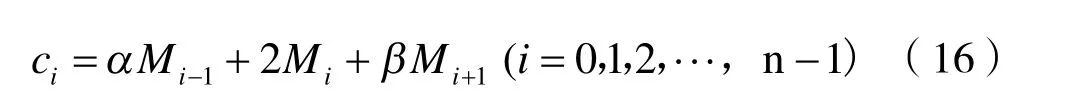
式中：

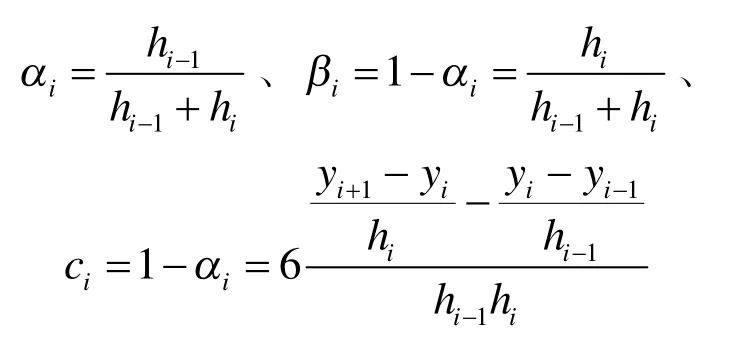
在式（16）中包含的n-1个方程里有n+1个未知数，为了确定全部参数，需要根据问题的实际情况，给出在端点处的边界条件。常用的边界条件有以下三种：

给定端点处的一阶导数值：

S′(x0)=y0′，S′(xn)=yn′

给定端点处的二阶导数值：

S′(x0)=y0′，S′ (xn)=yn′

特别地，若S′ (x0) =S′(xn)=0，则称为自然边界条件。

当f(x)是周期函数时，S(x)也为周期函数，此时边界条件为：

S(x0) =S(xn)、S′(x0) =S′(xn)、S′ (x0) =S′(xn)。

满足边界条件（1）时，可以得到下列两个方程：

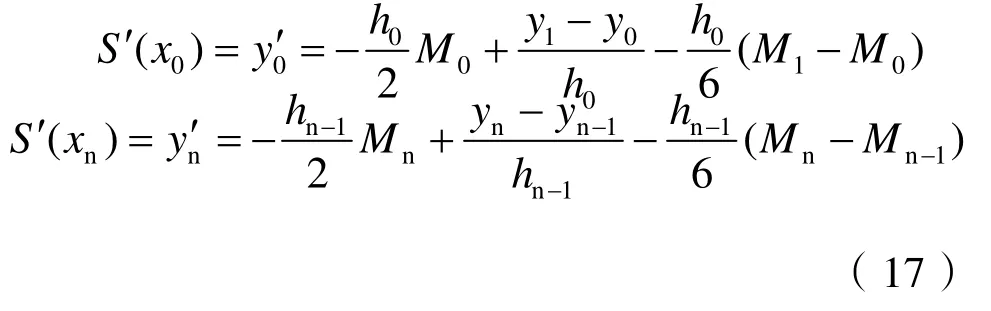
化简得：

联立式（16）和（18），即可求出关于参数Mi(i=0，1，2， ···，n )的n+1阶线性方程组。

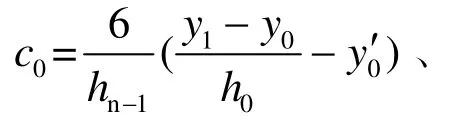
利用求解三对角方程组的追赶法进行求解，可以看出，方程组的系数矩阵都为严格对角占优矩阵，因此方程组有唯一的解。将解Mi带入式（13）即可获得三次样条函数。

3 伽马测井图像的生成与显示

方位伽马数据在进行深度修正、平滑和环境校正等预处理操作后，可用于地层岩性、地质构造的识别；通常采用成像图形方式进行显示和应用[13]。在钻井过程中，利用近钻头方位伽马成像图，可以较好地控制钻井风险，在构造不确定性高、横向变化较大的区块，能够清楚反映轨迹切割地层的关系，从而有效地预测地质构造的变化，指导井眼轨迹的调整。

3.1 设计伽马成像色谱

要实现随钻伽马值的成像，需要将插值处理后的伽马值根据规定的色度标定方法所定义的成像色谱转换成对应的颜色色标数据，将伽马值测量数据映射为颜色矩阵，再按颜色的深浅进行排列显示，通常暗色代表的是高伽马值，亮色代表低伽马值。之后，通过计算机图像学处理，可以提高成像测井图像结束结果的精度以满足在不同地质和地层情况的分析需求[14]。为了更加符合人的视觉特点，通常用色调（Hue）、色度（Satura–tion）和亮度（Intensity）组成的HIS颜色空间（图1）来表述颜色。

图1 伽马成像强度色谱

3.2 方位伽马图像的色度标定

方位伽马图像的色度标定采用静态色度，静态色度标定是对整个绘图井段内的伽马数据从最小值到最大值进行颜色的映射，以保证井段内所生成的伽马图像颜色与测量保持一致，静态色的标定适合在较大范围内观察地层的测井响应和岩性对比，虽然其清晰度在局部上表现较差，但静态色度标定可以清楚地反映地层放射性强度的整体变化趋势[15]。

4 程序实现和数据验证

使用LabVIEW软件分别对两种插值法的公式进行编程，将深度以及每个深度所对应的四个样本点数作为一组数据输入参数，由于使用Akima插值方法最少需要六个点才能绘制一段曲线，所以在上传至第四组数据之前都无法进行绘图。当得到第四组数据之后，根据四组数据的趋势，程序自动补足第一组数据之前的两组数据，得到六组数据后，便可以绘制深度方向上第一段曲线，往后钻井过程中每更新一组数据即可实时画出一段新的曲线，这里更新的一段新的曲线包括四个不同井周方向上的四条曲线，每一条曲线就是两组数据在深度方向上两点之间空缺的伽马值。在计算深度的最后一组数据时，会遇到和第一组数据一样缺少两组数据进行插值的问题，所以这里用同样的方法，根据最后四组数据的趋势，在最后一个点的后面补两组数据再进行插值，就可以计算出深度方向的最后一段曲线。得到深度方向上的连续曲线后，接下来进行井周方向的插值计算。任意选定一个深度，在四条深度曲线上得到四个数据点，使用三次样条插值计算出一条连接这四个点的平滑曲线，这条曲线就是某一深度井周360°上全部的伽马值。对深度曲线上的每一个深度进行三次样条插值的计算，可以得出深度和井周方向上全部的连续数据，以此来绘制强度图。选择辽河油田某一口井100～3 500 m的钻井数据，输入LabVIEW程序后画出伽马曲线图和成像图（图3）。在曲线图中，数据插值后得到了光滑过度的曲线，强度图中伽马值则在较低处成像偏亮，随着伽马值的升高，成像图由亮边暗，说明钻井进入高放射性地层。

图3 测井伽马值成像结果

为了验证程序在油区伽马值成像的准确性，选取同一口井4 660～4 690 m油层区域的伽马值进行成像处理（图4），可以看出，从4 660 m开始，随着深度的增加，上伽马值逐渐小于下伽马值，上下侧的伽马值的差值增大并且两条曲线出现明显的分离。可以判断，在深度4 660 m附近，钻头开始钻出油层底部，当深度到达4 667 m后，整个钻头完全钻出油层。此时应对钻头进行即时调整，使其回到油层区域。经过调整后，在深度4 675 m附近钻头又重新进入油层。但是通过观察后续的曲线可知，由于调整时井斜调整过度，钻头在深度4 683 m附近靠近油层顶部，即将钻出油层。此时需要再次调整钻井轨迹，确保钻头处于在目标层中钻进的状态直至完钻。利用随钻方位伽马成像处理技术，可以用图像准确显示整口井上的伽马值，提高对钻井轨迹的控制能力，更好地为旋转导向钻井服务。

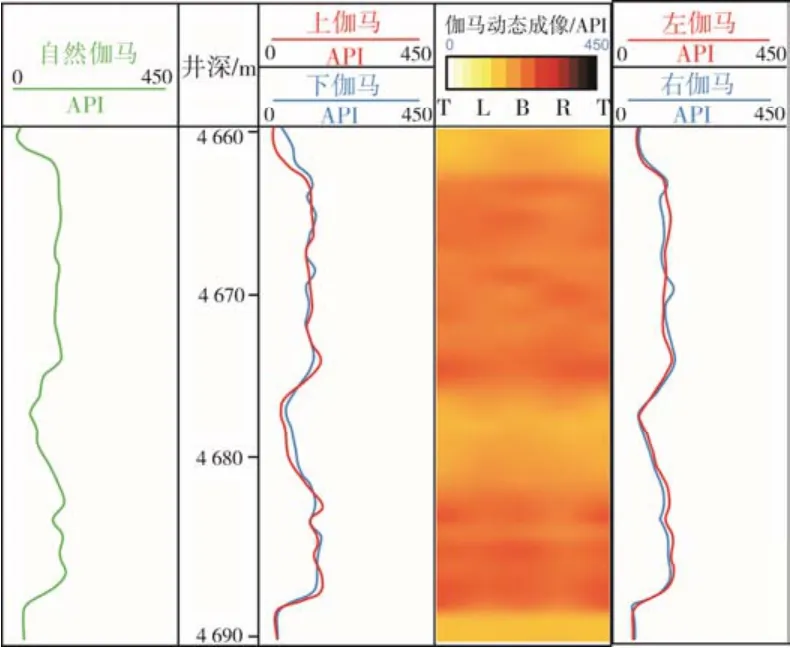
图4 油层区域伽马值成像

5 结论

本文基于复杂油气藏地质导向和随钻测量评价需求，利用LabVIEW软件，编写实现Akima插值和三次样条插值两种插值方法的程序，计算出深度和井周360°全方位的伽马测井曲线，根据插值的伽马数据转换成对应颜色的色标数据，将颜色数据按照坐标位置显示得到伽马值强度图。通过实际钻井数对程序进行测试，程序绘制的曲线图和强度图能够达到预期要求，可以对测井处地质和地层情况进行精确描述，从而为复杂油气勘探工作提供精确并且低成本的导向技术。