基于多期搜索蚁群算法的多区型仓库拣货路径优化

胡寒霖 张水旺 陈 康 傅宝洁 汪鹏飞

(安徽工业大学 管理科学与工程学院，安徽 马鞍山 243032)

0 引言

近年来，我国仓库的数量、种类和功能快速增长，但是仓库拣货效率与发达国家相比，还存在较大差距，这制约了我国物流服务业的快速发展。作为物流服务业的关键节点之一，仓库的拣货成本和拣货效率直接影响物流服务的整体效率。因此，对拣货路径问题进行优化，提高仓库拣货效率，具有较大的现实意义。

学者就路径优化问题作出了许多研究。方文婷等[1]在路径优化问题中，加入了节能减排，以总成本最小为研究目标，构造了一种混合蚁群算法，研究了冷链物流配送路径优化问题；马冰山等[2]结合多配送中心联合服务模式的特点和纯电动物流车辆的行驶特征，针对半开放式多配送中心纯电动车路径优化问题进行深入的研究；任腾等[3]在研究路径优化问题时，考虑了冷链配送客户满意度，同时以车辆载重、客户时间窗和冷链产品变质率为约束，构建了以碳排放量最小为优化目标的路径优化模型，并通过改进型蚁群算法对该问题进行了求解；胡春阳等[4]采用改进的蚁群算法对AGV路径规划进行求解；郑娟毅等[5]将蚁群算法与遗传算法相结合，提出了一种改进的混合遗传蚁群算法，解决了不同规模的旅行商问题；任腾等[6]在前述研究的基础上，同时考虑顾客满意度和道路拥堵状况，针对冷链车辆路径优化问题，设计了一种新的知识型蚁群算法。

在路径优化问题上，除了采用改进的蚁群算法进行求解，还有混合粒子群算法[7]、人工鱼群算法[8-9]、遗传算法[10]、多种遗传算法[11]、启发式算法等[12]。基于上述成果，本文针对仓库拣货路径问题进行研究。以拣货路径距离最短为目标函数，建立多区型仓库拣货路径优化模型，提出改进的多期搜索蚁群算法，规避蚁群算法容易陷入局部最优而导致算法过早停滞的现象，通过对比传统蚁群算法、自适应动态搜索蚁群算法和多期搜索蚁群算法求解效率，验证多期搜索蚁群算法的优越性。

1 问题描述

多区型仓库由若干相互平行的主通道与巷道组成，货架平行分布在巷道两侧，集货点设置在仓库的左下角。仓库平面图如图1所示，数组{A,R,G}表示相应的储位编号，其中A为货物所在区，R为货物所在行，G为货物所在列。例如{2，3，5}表示货物位于2区、3行、5列。

2 模型构建

2.1 基本假设

(1) 每个储位只储存一种商品。

(2) 拣货车存在容量限制，且拣货车容量均相等。

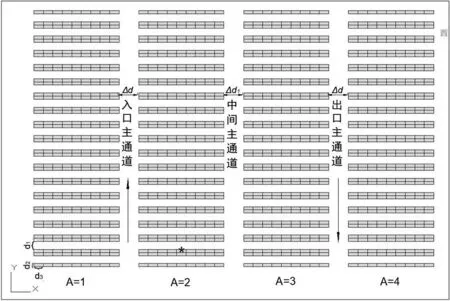
图1 多区型仓库平面示意图

(3) 每个储位上的拣选商品需一次拣选完毕，不得拆分为多次拣选。

2.2 参数设置

H：点的集合；

I：边的集合；

D：距离矩阵；

N：拣货点编号集合，N=(H,I,D)；

vi：第i个储位，其中v1为集货点，v(n+1)为最后一个拣货点；

dvivj：储位vi到储位vj的最短折线距离；

Q'：拣货小车额定载重量；

m：子路径总数(拣货车数量)；

k：子路径编号；

2.3 数学模型

假设拣货员从v1开始拣货，当到达vn时小车载重量超过Q'，则在序列的n个元素前增加一个起点，并从第n个元素开始重新计算载重，最终形成一个由若干条路径组合而成，且满足小车载重的约束。基于此，以拣货路径距离最短为目标[13]，构建数学模型如下：

(1)

s.t.

(2)

(3)

(4)

(5)

xvivj∈{0,1}

(6)

其中，k=1,2,…m，i,j=1,2,…n+1。

式(1)表示目标函数，为求解总路程最短路径；式(2)表示货物装载量之和需小于拣货车额定载重量；式(3)、式(4)表示每个点有且仅有一次通过机会；式(5)表示不存在最小回路；式(6)表示决策变量xvivj可能的取值，当xvivj为1时，表示拣货过程中经过了i和j两个点，当xvivj为0时，表示拣货过程中未经过i和j两个点。

3 改进蚁群算法

3.1 基本蚁群算法

蚁群系统是由Dorigo、Maniezzo等[14]于20世纪90年代首先提出来的。自然界中蚁群可以克服地势及距离的重重阻碍，在洞穴与食物之间找到一条最佳路径，究其根本是因为蚁群中存在一套以“信息素”为核心的反馈机制，这种机制能够合理挖掘潜在路径并充分利用，最终找到一条较佳路径，蚁群算法应运而生。它在TSP问题上具有良好的适应性，同时也适用于TSP问题衍生出的多回路问题，即VRP问题。

(7)

τij(t+n)=(1-ρ)τij(t)+△τij(t)

(8)

(9)

(10)

3.2 算法改进

基本蚁群算法针对VRP问题具有良好的适应性，但其仍具有一定的局限性，主要表现在当问题规模较大时，算法容易陷入局部最优化从而导致算法过早的停滞。文献提出一种动态自适应搜索蚁群算法[15]，能有效解决早熟问题，但仍有优化空间。本文基于原有算法提出多期搜索蚁群算法模型，用以引导算法探索最优路径和提高算法的收敛性能。

3.2.1 分段式信息素强度

单独标志的序号放在引文责任人之后，且设置其格式为上标，阐述中出现的引文序号不需要上标，正文中的引用文献若需指明文献责任人，则仅需写出第一责任人，外文文献仅需写出其姓氏即可。

由蚁群算法的特性可知，当出现一只蚂蚁在一条路径上觅食很久时，放置一个更近的食物基本没有效果，其原因可以理解为当初一只蚂蚁留下了较为浓烈的信息素，此后一段时间大量蚂蚁均选择了这条路线，该路线上的信息素浓度不断升高。这时即使有一只蚂蚁找到更近的路径，由于时间间隔过久，两条路径上的信息素浓度相差较大，整个系统基本已经停滞了，陷入局部最优。因此，本文中采用式(11)的分段函数Qi来替代式(10)中的固定常数Q：

(11)

当函数最优值处于一段时间没有持续变化时，说明搜索可能陷入了局部最优。故将蚁群算法的完整迭代过程分为若干个“搜索期”，其中Ti为第i个搜索期的结束时间。在进入新的搜索期后改变信息素常量，使得信息素浓度处在较高水平时，新发现的较优路径仍能给蚁群提供较好的指导性，从而避免陷入局部误区。

3.2.2 信息素导向与启发信息的权重比例

本文针对原有的信息素导向与启发信息之间的固定权重提出以下改进方法：

当t≤T1时，信息素导向和启发信息权重分别为：

(12)

当t>T1时，信息素导向和启发信息权重分别为：

(13)

在同一搜索期内，随着迭代次数的增加，信息素权重μ与启发信息权重η的比重不断变化。当蚁群完成一段搜索期后，信息素权重会产生一个负向的“跳变”，启发信息权重会产生一个正向的“跳变”，其中k1和k2为信息素调整数与启发信息调整系数，决定着“跳变”的大小和新一轮搜索期内μ与η的比例。在Q、μ与η的共同作用下，同一搜索期前期算法侧重于对新路径的随机选择，而在后期更侧重于对较好路径的深度挖掘，从而完成参数的自适应。

3.2.3 转移概率

针对转移概率，本文进行如式(14)所示的转移规则，进行改进。

(14)

4 算例分析

4.1 算例求解

对淘宝某电商仓调研得到的数据进行整理，求解货架与货架间的最短路径。设置初始参数，将模型与相应数据相结合，迭代150次后，得到最终路径规划方案如图2所示。

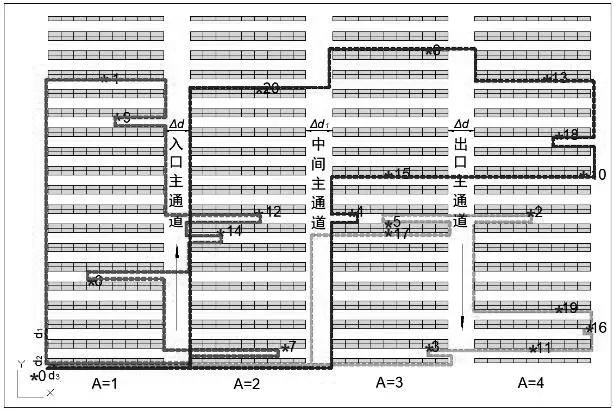
图2 拣货路径示意图

基于本文算法求得，路线总长为832米，最佳的拣货路径为：

拣货路径1：(0,6,14,12,4,5,15,20,9,0)；

拣货路径2：(0,1,8,13,18,10,2,17,3,0)；

拣货路径3：(0,11,16,19,7,0)。

该仓库目前采用的是“U+返回”型拣货策略，同样的数据，“U+返回”型拣货策略的拣货路线总长为937.6米。因此，本文方法可以提升该仓12.7%的作业效率，说明本文方法能有效节约拣货路径。

4.2 结果分析

为验证算法改进前后的优越性，本文随机生成一组40货位的订单，拣货点信息如表1所示，采用传统蚁群算法(ACO)、自适应动态搜索蚁群算法(ADACO)和多期搜索蚁群算法(MSACO)分别求解10次，结果如表2所示。

表1 拣货点信息

表2 不同算法运行结果汇总

从表2可以看出，ACO算法的配送成本的最佳值仅有965.2，且收敛代数与运行时间有着较大的起伏，算法不具备稳定性；ADACO算法的拣货成本集中于930附近，但其收敛代数较高，运行时间较长；MSACO在保证拣货成本较低的前提下，迭代次数较ADACO节约了14.93%，其求解结果处于910～940之间，具有良好的稳定性。

图3显示出3种算法的收敛曲线，由曲线可以看出传统ACO算法较早陷入局部最优并停滞；ADACO具有良好的跳出局部最优的能力，但在迭代后期挖掘潜能欠佳；MSACO算法对新的路径具有较好的挖掘能力，能有效解决蚁群算法的“早熟”问题。

图3 最小成本变化趋势对比

5 结语

本文针对多区型仓库拣货路径优化问题构建了数学模型，提出改进的多期搜索蚁群算法，经仿真实验对比结果可以看出，改进的多期搜索蚁群算法在拣货路径优化问题上具有一定的优越性。后续将基于算法去探索其他路径优化问题，尤其一些更为复杂的路径优化问题。