大幅面集成成像显示系统中宏透镜阵列位置误差度量与校正

毛 岩，燕 展，刘新蕾，荆 涛，黄应清，蒋晓瑜，闫兴鹏

（陆军装甲兵学院 信息通信系，北京100072）

1 引 言

集成成像三维显示具有稳定性高、实现成本较低、不受外界光照干扰、便于研发和实际应用等优点，其不需要佩戴设备就能观看全视差、彩色、视点无跳变的三维场景［1］，也不需要相干光源就可以实现多人观看。

集成成像系统中使用的透镜阵列，通常有微透镜阵列和宏透镜阵列。微透镜阵列透镜间距通常小于3 mm，在集成成像中应用广泛。因此，关于集成成像中微透镜阵列的相关研究［2-4］较多。然而，微透镜阵列视场角非常有限，一旦超出有效视场角，将会产生视区跳变，这表明使用微透镜阵列难以实现精确的大幅面集成成像三维显示。随着研究的不断发展，越来越多的研究人员开始在大幅面集成成像系统中使用宏透镜阵列。宏透镜阵列一般是通过机械方式内嵌在硬质基板上，其优点是成本低、制作工艺成熟，可以实现大幅面、宽视场角的集成成像显示，不足是安装或使用造成的位置误差较大。因此，为获得更好的显示效果，需要对宏透镜阵列的位置误差进行度量与校正。

2004 年，Arai 等人［5］分析了单元透镜位置误差作用下单元图像再现的局部和全局误差。同年，Heejin Choi 等人［6］提出了一种使用阶梯透镜阵列（SLA）或复合透镜阵列（CLA）的方法，从而增加了重建图像的深度，随后又在2014 年，提出了一种使用偏移透镜阵列和垂直栅栏提高三维图像质量的新技术［7］，所提出的系统适合于实现具有高像素密度的平铺整体浮动显示器。2016 年，Jae-Young Jang 等人［8］设计了一种新的深度优先集成成像系统，该系统的透镜阵列由3 个子透镜配置组成，并引入了一种新的子像素重排算法，减少了三维图像的彩色伪影。同年，Song Min-Ho 等 人［9］设 计 了 一 种 自 适 应 透 镜 阵列，该阵列由多个以弯曲形状排列且曲率半径可调的平面透镜阵列组成，可以解决使用曲面透镜阵列时出现的间隙不匹配问题。在国内，2017年，北京邮电大学的高鑫等人［10］提出了一种360°光场三维显示系统，得出了像素、三维物体和观看位置之间的映射关系，并将“基本像差理论”和“阻尼最小二乘法”用于光学分析和透镜设计，有效地抑制了像差。2018 年，杨神武等人［11］借助LED 面板（尺寸为3 840 像素×2 160 像素），展示了基于非球面透镜阵列和全息功能屏的大规模水平光场显示器，其可以显示高质量的三维图像。同年，郭敏［12］提出了基于胶合透镜阵列的集成成像显示方法，增加了透镜阵列搭建的灵活性，并构建了采集图像与立体元图像之间的光学映射模型，从实现机理上解决了深度反转问题。2019 年，闫兴鹏等人［13］研究了宏透镜阵列横向位置误差，通过LCD 平面上像素与透镜阵列中透镜中心实际位置的连线，重构实际光线与研究平面的交点。2020 年，文军等人［14］比较了矩形排列的透镜阵列和六边形排列的透镜阵列的视点数量和每个视点的分辨率，研究表明后一种透镜布置可以提高视点图像的分辨率，而不会明显降低视点的数量。同年，王悦迪等人［15］设计了一种基于双凸透镜阵列和全息功能屏的光场显示系统，该系统可以再生具有大水平视角和高视角的高视点密度三维光场。系统中引入了双凸透镜阵列，以扩展关键的水平视角并改善立体感。2021 年，燕展等人［16］提出采用散斑面积来度量宏透镜阵列轴向位置误差，并对宏透镜阵列轴向位置误差提出了补偿的方法。

2 宏透镜阵列位置误差度量

现有研究表明，在集成成像系统中采用宏透镜阵列，重构光场方向性信息依赖于宏透镜阵列与基元图像的相对位置关系。如图1（a）所示，宏透镜阵列规则排布，相邻单元透镜之间间距相等，为理想值pD。任意单元透镜与LCD 之间的距离相同，为理想值g，此时没有位置误差。然而，实际上，因为安装和操作，透镜阵列不可避免地产生位置误差。图1（b）中，宏透镜阵列在垂直于LCD 平面的方向上存在位置误差，单元透镜Ln-1、Ln+1到LCD 平面的距离分别为g+Δn-1、g+Δn，与理想值g存在误差，定义这类误差为轴向位置误差。图1（c）中，宏透镜阵列在平行于LCD 平面的方向上存在位置误差，单元透镜Ln-1和Ln、Ln和Ln+1之间的间 距分别为pD+Δdn-1、pD+Δdn，与理想值pD存在误差，定义这类误差为横向位置误差。

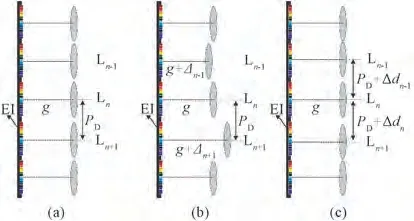
图1 宏透镜阵列的空间位置误差示意图。（a）没有位置误差；（b）轴向位置误差；（c）横向位置误差。Fig.1 Schematic diagram of spatial position error of macro lens array.（a）Free position error；（b）Axial position error；（c）Lateral position error.

2.1 宏透镜阵列轴向位置误差度量

在理想情况下，宏透镜阵列无位置误差表征如图2 所示，以透镜阵列局部为例，理想的显示端透镜中心位置分别为a、b、c，以点b 为原点O，分别以平行于透镜阵列行、列方向为X、Y轴，以垂直透镜阵列方向为Z轴，建立空间直角坐标系，透镜阵列行、列间距为w、l，透镜阵列、LCD 所在平面深度为0、z1。LCD 平面上D、E、F 三点经过对应的透镜中心a、b、c，在中心深度平面上形成重构点R。

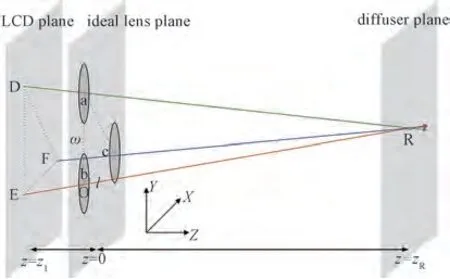
图2 宏透镜阵列无位置误差表征Fig.2 Free position error characterization of macro lens array

假设原透镜阵列中心a、b、c坐标为(xa，ya，0)、(xb，yb，0)、(xc，yc，0)，则存在以下关系：

xa=xb=0，xc=l， （1）

ya=w，yb=yc=0 . （2）

假设空间任一重构点R 坐标为(xR，yR，zR)，则直线aR的参数方程可以表示如下：

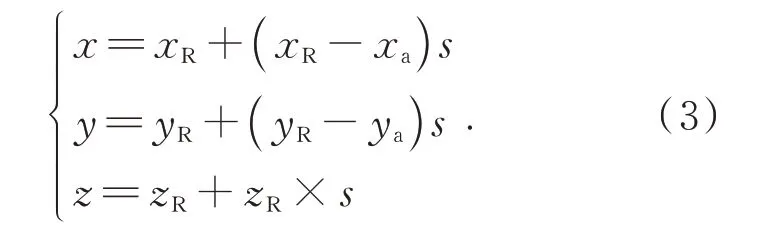
同理可得直线bR、cR的参数方程。记直线aR、bR、cR分别与LCD 平面相交于点D(xD，yD，z1)、E(xE，yE，z1)、F(xF，yF，z1)，其对应直线参数方程的参数分别为s1、s2、s3，则存在以下关系

z1=zR+zR×s1=zR+zR×s2=zR+zR×s3. （4）

由公式（4）可得，s1=s2=s3。由此，可求出点D、E、F 对应坐标。实际情况下，显示过程中宏透镜阵列轴向位置误差表征如图3 所示。只考虑轴向位置误差，即透镜阵列中心只在垂直于LCD 平面的方向上存在位置误差时，点D、E、F发出的光锥将不在深度平面上汇聚，即点D、E、F发出的光锥经过透镜阵列上有偏差的实际透镜A、B、C，分别与点R 所在深度平面相交于点d、e、f。显然，线段dR、eR、fR的平均值和方差越大，轴向位置误差越大，因此可以用线段dR、eR、fR的平均值和方差来度量透镜阵列轴向位置误差。

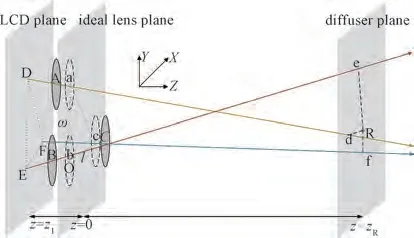
图3 宏透镜阵列轴向位置误差表征Fig.3 Axial position error characterization of macro lens array

记透镜阵列中心实际点A、B、C 坐标为(xA，yA，zA)、(xB，yB，zB)、(xC，yC，zC)，则

xA=xB=0，xC=l， （5）

yA=w，yB=yC=0 . （6）

直线AD的参数方程为

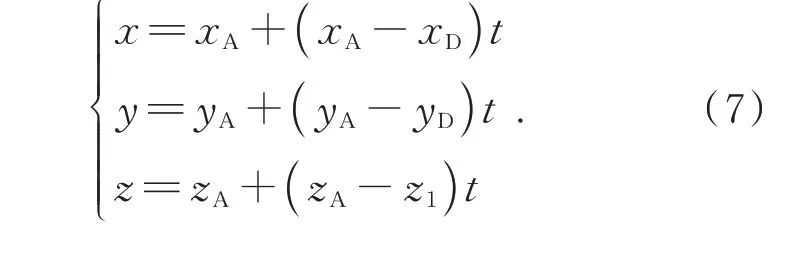
同理可得直线BE、CF的参数方程。直线AD、BE、CF与 点R 所 在 深 度 平 面 相 交 于 点d(xd，yd，zd)、e(xe，ye，ze)、f(xf，yf，zf)，其 对 应 直线参数方程的参数分别为t1、t2、t3。因为点d 在点R 所在深度平面上，故有

zd=ze=zf=zR. （8）

结合公式（7）和（8），可以求得t1，从而得到点d 坐标。同样地，可以得到点e、f 坐标，记线段dR、eR、fR的距离分别为d1、d2、d3，则

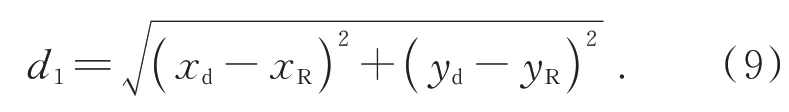
同理可得d2、d3，记线段dR、eR、fR的平均值分别为davg，则

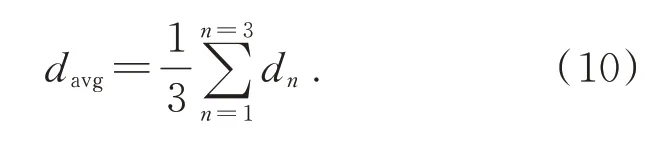
对应的方差dvar为

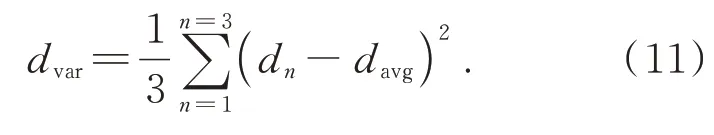
2.2 宏透镜阵列横向位置误差度量

实际情况下，显示过程中宏透镜阵列横向位置误差表征如图4 所示。只考虑横向位置误差，即透镜阵列中心只在平行于LCD 平面的方向上存在位置误差时，点D、E、F 发出的光锥经过透镜阵列上有偏差的实际透镜A、B、C，分别与点R所在深度平面相交于点d、e、f。同样地，线段dR、eR、fR的平均值和方差越大，横向位置误差越大，因此仍可以用线段dR、eR、fR的平均值和方差来度量透镜阵列横向位置误差。

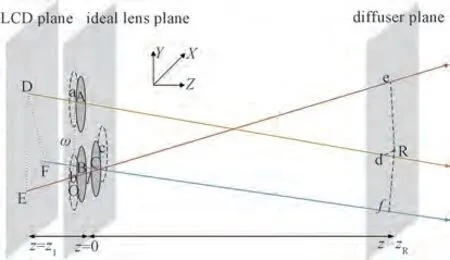
图4 宏透镜阵列横向位置误差表征Fig.4 Lateral position error characterization of macro lens array

记透镜阵列中心实际点A、B、C 的坐标为(xA，yA，zA)、(xB，yB，zB)、(xC，yC，zC)，则

zA=zB=zC=0 . （12）

横向位置误差分析过程与轴向位置误差分析时基本一致，通过直线AD、BE、CF的参数方程，分别用参数t1、t2、t3表示点d、e、f 坐标，因为点d、e、f 在点R 所在中心深度平面上，结合公式（7）和（8），可以求得t1，从而得到点d 坐标。同样地，可以得到点e、f 坐标，从而得到线段dR、eR、fR距离d1、d2、d3，根据公式（10）和（11），最终求得线段dR、eR、fR的平均值davg和对应的方差dvar。

3 透镜位置误差校正

3.1 轴向位置误差校正

集成成像显示时，全息功能屏可以用来接收所成的像，通过调整全息功能屏的位置来测量轴向位置误差。如图5 所示，以LCD 平面上点o 为原点，过LCD 平面且垂直于透镜主光轴所在直线为x轴，平行于透镜主光轴所在直线为z轴，透镜中心与LCD 显示屏的理想轴向距离为g，实际轴向距离为gr。单元透镜中心横向坐标为d，选取其所对应的基元图像中心上方某一像素，像素中心的x坐标为xS，调整全息功能屏，使得像素在全息功能屏上成像，且像的底部落在z轴上，此时全息功能屏与LCD 显示屏的轴向距离分别为l。

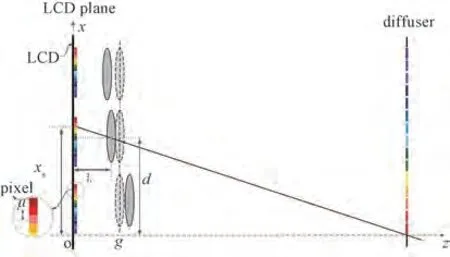
图5 透镜阵列中单元透镜轴向位置测量示意图Fig.5 Schematic diagram of measuring unit lens' axial position in lens array

根据几何关系，透镜的轴向位置可表示为

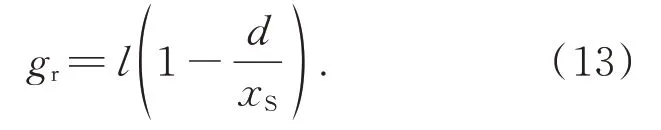
利用公式（13）即可获得实际的轴向位置。对于每个单元透镜，都通过调整全息功能屏，从而实现宏透镜阵列轴向位置误差的测量。在对轴向位置误差测量的基础上，对其进行校正。当获得单元透镜中心实际位置与LCD 平面的轴向位置gr后，轴向位置误差可以通过重排单元透镜对应的基元图像像素点位置的方式进行校正。如图6 所示，虚线透镜为理想透镜位置，实线透镜为实际透镜位置，重构像点R 坐标为(xR，zR)。理想情况下对应的像素与单元透镜Ln-1中心的横向距离为Δxideal，为确保像素仍能在点R 成像，该像素经过校正后与单元透镜Ln-1中心的横向距离为Δxcorrect。

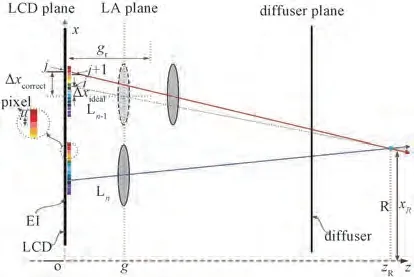
图6 轴向位置误差校正原理Fig.6 Principle of axial position error correction

根据几何关系，此时存在以下关系：

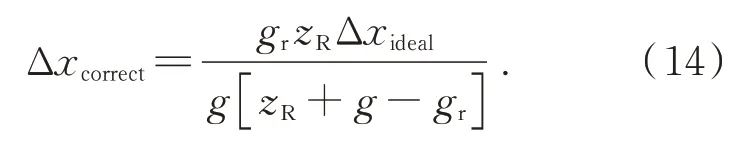
当透镜中心理想位置所在平面与重构点的距离较大且远大于透镜阵列的轴向位置误差，即zR≫g-gr时，则公式（14）可以简化为：

此时，轴向位置误差的校正与重构点所在位置无关，仅与单元透镜中心理想位置、实际位置与LCD 平面的轴向位置有关。记理想像素在该基元图像中序号为i，校正后像素在该基元图像中序号为j，每个基元图像的像素个数为n，根据公式（15），可得

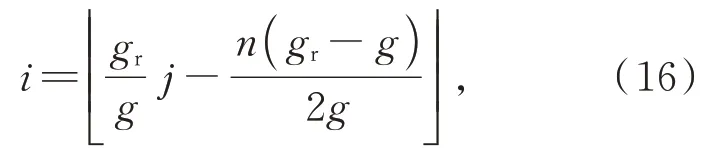
3.2 横向位置误差校正

结合上述对单元透镜横向位置误差显示过程分析，仍然通过调整全息功能屏的位置来测量横向位置误差。当全息功能屏在不同深度位置移动时，像的位置将会发生变化。这里，因为像素的间隙被放大，所以不同像素能够辨认。因此，可以通过像的位置变化测量透镜阵列横向位置误差。

如图7 所示，透镜阵列与LCD 显示屏的轴向距离为g；与全息功能屏位置1 和位置2 的轴向距离分别为l1、l2；选取合适数量像素，μ为像素间隔大小，n为像素的间隔数量。当全息功能屏放置在位置1 时，一定数量像素在全息功能屏上成像。调整全息功能屏于位置2 处，使得这些像素在全息功能屏上成像，且像的底部落在z轴上，底部像素的横向位置变化为Δsbottom，单元透镜横向位置坐标为d，由此，透镜横向位置可表示为

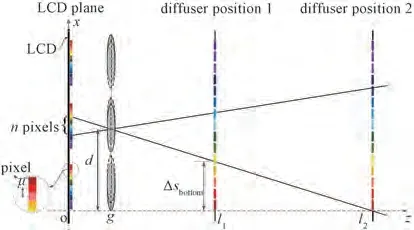
图7 透镜阵列中单元透镜横向位置测量示意图Fig.7 Schematic diagram of measuring unit lens' lateral position in lens array

利用公式（17），即可获得实际的横向位置，从而可以实现宏透镜阵列横向位置误差的测量。在对横向位置误差测量的基础上，对其进行校正。当获得单元透镜的横向位置d后，可以按照理想重构点位置和真实横向位置得到正确的像素位置，因此，横向位置误差可以通过重排对应的基元图像像素点位置的方式进行校正。如图8所示，理想情况下对应的像素横向坐标为xideal，为确保像素仍能在点R 成像，该像素经过校正后的横向坐标应为xcorrect。

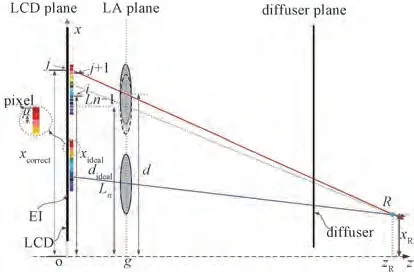
图8 横向位置误差校正原理Fig.8 Principle of lateral position error correction

根据几何关系，此时存在以下关系：

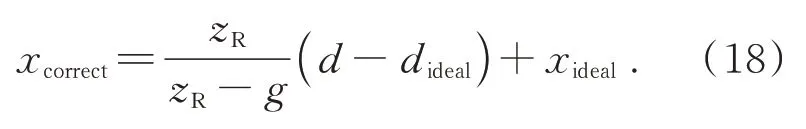
当透镜中心理想位置所在平面与重构点的距离较大且远大于透镜阵列与LCD 平面的距离，即zR≫g时，则公式（18）可以简化为：

xcorrect=d-dideal+xideal. （19）

此时，横向位置误差的校正与重构点所在位置无关，仅与单元透镜的横向位置有关，这使得校正更加简单。记理想像素在该基元图像中序号为i，校正后像素在该基元图像中序号为j，像素大小为μ，根据公式（19），可得

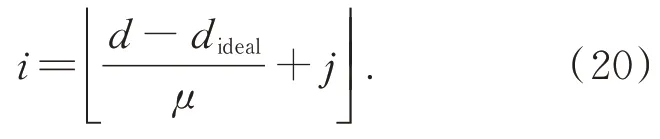
根据公式（20）可以发现，理想像素在该基元图像中序号i和校正后像素在该基元图像中序号j呈线性关系，也就是说，对于同一基元图像，只要将其像素移动相同的横向距离，就可以实现横向位置误差的校正。

4 实验与结果分析

4.1 宏透镜阵列位置误差度量仿真

结合下步实验所用装置参数，对宏透镜阵列轴向位置误差下的距离的平均值和方差进行仿真。透镜阵列行间距和列间距相等，记为pD，理想情况下LCD 到透镜阵列中心所在平面距离g=-z1=11.5 mm。以单元透镜b 作为参考，单元 透 镜a、c 的 误 差 分 别 为Δg1、Δg2，其 范 围都为[-0.1g，0 .1g]。

如图10 所示，水平、垂直方向代表的物理含义不变，距离的方差用颜色表示，每幅图像中颜色代表的数值仍由图像右侧的图例给出。同样地，每幅图像高度对称。观察每幅图像的中心，发现当都为0 时，即没有轴向位置误差时，距离的方差为0，与理想情况一致。在参考透镜视场角范围内，比较图10（a）和（b），在相同的轴向位置误差下，重构点在X方向上越偏离参考透镜，距离的方差越大，即受到的影响越大，结论在图10（c）和（d）上也得到了验证；同样地，比图10（a）和（c），在相同的轴向位置误差下，重构点在Y方向上越偏离参考透镜，距离的方差越大，即受到的影响越大，结论在图10（b）和（d）上也得到了验证；比较图10（a）和（e），在相同的轴向位置误差下，重构点在Z方向上越偏离参考透镜，对应的距离方差越小，即受到的影响越小，结论在图10（d）和（h）、（f）和（g）上也得到了验证；比较图10（a）和（f）、（e）和（g），在相同的轴向位置误差下，透镜阵列中单元透镜间距pD越大，对应的距离方差越小，即受到的影响越小；而在图10（d）和（i）中，结论刚好相反，在相同的轴向位置误差下，透镜阵列中单元透镜间距pD越大，对应的距离方差越大，即受到的影响越大，同样表明单元透镜间距pD对距离平均值的影响是复杂的，不存在简单的正相关或者负相关关系。

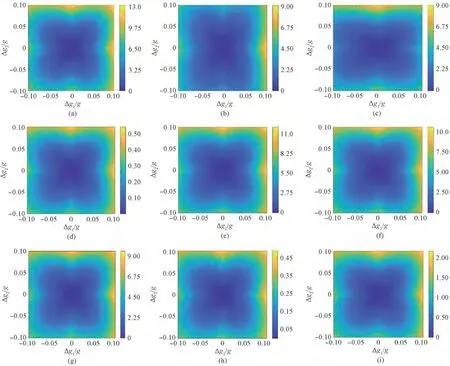
图10 不 同 参 数 下，距 离 的 方 差（单 位 为mm）。（a）(xR，yR，zR，pD)=(50，50，100，12.6)；（b）(xR，yR，zR，pD)=(0，50，100，12.6)；（c）(xR，yR，zR，pD)=(50，0，100，12.6)；（d）(xR，yR，zR，pD)=(0，0，100，12.6)；（e）(xR，yR，zR，pD)=(50，50，200，12.6 )；(f)(xR，yR，zR，pD)=( 50，50，100，25.2 )；(g)(x R，yR，zR，pD)=( 50，50，200，25.2 )；(h)(xR，yR，zR，pD)=( 0，0，200，12.6 )；(i)(x R，yR，zR，pD)=( 0，0，100，25.2 )。Fig.10 Aariance of distance under different parameters（mm）.（a）(xR，yR，zR，pD)=(50，50，100，12.6)；（b）(xR，yR，zR，p D)=(0，50，100，12.6)；（c）(xR，yR，zR，pD)=(50，0，100，12.6)；（d）(xR，yR，zR，pD)=(0，0，100，12.6)；（e）(xR，yR，zR，pD)=(50，50，200，12.6)；（f）(xR，yR，zR，pD)=(50，50，100，25.2)；（g）(xR，yR，zR，pD)=(50，50，200，25.2)；（h）(xR，yR，zR，pD)=(0，0，200，12.6)；（i）(xR，yR，zR，pD)=(0，0，100，25.2).

宏透镜阵列横向位置误差涉及X、Y两个方向。如果X、Y两个方向都有误差，则引入的变量较多。因此，仿真分析时，可只在其中一个方向产生误差，具体分析过程与轴向位置误差相似，这里不再讨论。

4.2 宏透镜阵列位置误差校正实验

通过上面分析，可知宏透镜阵列横向位置误差校准较为简单，对于同一基元图像，只要将其所有像素移动相同的横向距离，就可以实现横向位置误差的校正。显示系统装置如图11 所示，其由LCD 屏、宏透镜阵列和全息功能屏组成，LCD显示屏分辨率为3 840×2 160，其像素尺寸为0.072 mm，宏透镜阵列呈矩形排布，13 行22 列，宏透镜阵列中单元透镜半径为5 mm，焦距为10 mm，上下、左右间距都为12.6 mm，视场角为60°，LCD 显示屏与宏透镜阵列中心所在平面的轴向距离理想值为11.5 mm。

图11 显示系统装置Fig.11 Display system device

实验中，将基元图像中心“+”字点亮，“+”字成规则排布，按照上述方法进行显示，计算宏透镜阵列中各单元透镜的横向位置，从而得到宏透镜阵列横向位置误差。随后，利用所提方法对宏透镜阵列横向位置误差进行校正，并通过对比校正前后的三维再现效果进行验证。观察校正前和校正后的三维再现效果（图12），没有校正横向位置误差时的显示效果如图12（a）所示，利用所提方法进行横向位置测量和补偿后的显示效果如图12（b）所示。可以看出，校正前，由于横向位置误差的存在，再现图像中“+”字排列不再规则，局部成像位置甚至产生严重的畸变，而校正后，再现图像中“+”字排列较为规则，缓解了横向位置误差所引起成像位置的畸变。

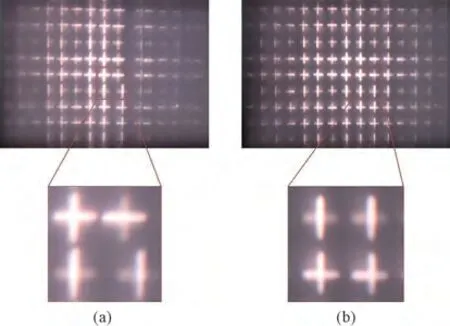
图12 横向位置误差对比。（a）校正前；（b）校正后。Fig.12 Comparison of lateral position errors.（a）Befor ecorrection；（b）After correction.

下面进行宏透镜阵列轴向位置误差校正实验。实验中，同样将基元图像中心“+”字点亮，“+”字成规则排布，按照上述方法进行显示，计算宏透镜阵列中各单元透镜的轴向位置，从而得到宏透镜阵列轴向位置误差。设置的虚拟相机阵列大小为77×77，总体成正方形排列，相邻相机间距4 mm，相机视场角为60°，采集相机拍摄图片的像素分辨率为501×501。设置的虚拟场景由半径为10 mm 的排球组成，排球表面为红、黄、蓝相间的块状拼接而成，场景正面图像如图13 所示。

图13 虚拟场景正面图像Fig.13 Frontal image of virtual scene

排球中心距离虚拟相机阵列所在平面为160 mm。运用SPOC 算法合成新的基元图像阵列时，参考面设置距离拍摄阵列160 mm 处，即排球中心所在位置。将合成的基元图像阵列进行三维再现，观察校正前和校正后的三维再现效果（图14），没有校正误差时的显示效果如图14（a）所示，利用所提方法进行轴向位置测量和补偿后的显示效果如图14（b）所示。可以看出，校正前，由于轴向位置误差的存在，再现的排球形状出现了一定畸变，且块间的分界线模糊不清，出现重影；而校正后，再现的排球形状更圆润，与模型更为相似，并且块间的分界线较为清晰，重影现象得到了缓解。

图14 轴向位置误差对比。（a）校正前；（b）校正后。Fig.14 Comparison of axial position errors.（a）Before correction；（b）After correction.

5 结 论

本文分析了宏透镜阵列位置误差对集成成像显示效果的影响，针对宏透镜阵列位置误差，将其分为轴向位置误差和横向位置误差。选择透镜阵列局部，光线从该局部透镜阵列中各单元透镜对应的基元图像像素出发，经过各单元透镜中心，在空间中汇聚于一点。当存在位置误差时，这些像素将在其他点处成像，本文通过重构点到这些点的距离的平均值和方差来度量位置误差，从而实现了对宏透镜阵列位置误差的表征。其次，通过移动全息功能屏来变化像的位置和大小，实现了对宏透镜阵列轴向位置和横向位置的测量，将其与理想轴向位置和横向位置作差，从而实现了对宏透镜阵列轴向位置误差和横向位置误差的测量。接着，分析了宏透镜阵列轴向位置误差和横向位置误差下，理想像素序号与校正后的补偿像素序号之间的关系，实现了宏透镜阵列位置误差的校正。最后，通过仿真对宏透镜阵列位置误差进行了度量，并通过实际显示效果验证了校正方法的有效性。